Activer le mode zen
Ressource au format PDF
Mots-clés
Classification
Comment faire une horloge avec un glaçon ?
03/10/2022
Résumé
Il est possible de piéger un glaçon entre deux huiles de densités différentes. Il se met alors à fondre en lâchant des gouttes. Dans cet article, nous étudions ce problème et montrons qu'il est possible de déterminer avec précision les instants auxquels les gouttes se détachent, afin d'en faire une horloge.
Table des matières
Lors de notre année de Master 1 en Sciences de la Matière à l'ENS de Lyon et dans le cadre de notre cursus nous avons pu participer au Tournoi international des physiciens 2021 (IPT 2021). Ce tournoi propose de s'intéresser à différentes problèmes. Dans cet article nous allons présenter notre étude de l'horloge à glaçon.
1. Position du problème
Voici le problème tel qu'il était posé dans le cadre du tournoi :
Source : IPT 2021. Voir la vidéo "Ice Cube Experiment" sur la chaîne Home Science.
Figure 1. Ice clock problem
2. Questionnements sur le phénomène
On peut tout d'abord s'interroger sur cycle de l'horloge, pour déterminer quels phénomènes sont le moteur des oscillations du glaçon ?
Sur la vidéo de la figure 2, on observe le glaçon en train de fondre qui oscille dans un bain d'huiles dont la densité augmente du haut vers le bas du verre. Lorsque le glaçon fond, de l'eau s'accumule à sa base et le système {glaçon + goutte} descend dans le verre. On observe ensuite que le détachement de la goutte provoque la remontée du glaçon.
Ainsi le moteur des oscillations du glaçon repose sur la variation de la masse volumique du système {glaçon + goutte} dans le gardient de densité du bain d'huile, figure 4. Lorsque le système est composé uniquement de glace, le glaçon se trouve dans une position d'équilibre dans le bain d'huile. Lorsqu'il fond et qu'une goutte se forme à sa base, la masse volumique de l'eau étant plus grande que celle de la glace, la masse volumique du système {glaçon + goutte} devient plus grande et le système descend. Il ne descend pas jusqu'au fond du verre car la masse volumique de l'huile 2 reste plus grande que celle du système. Une fois que la goutte se détache, le glaçon remonte, la masse volumique du système de nouveau composé uniquement de glace est plus petite mais moins que celle de l'huile 1. On a :
$$ \rho_{\mathsf{huile1}} < \rho_{\mathsf{glace}} < \rho_{\mathsf{huile2}} < \rho_{\mathsf{eau~liquide}}$$
On pourrait aussi raisonner en terme de forces appliquées sur le glaçon. L'eau a la particularité de se solidifier en augmentant son volume. Ainsi, le système lorsqu'il est entièrement composé de glace ou lorsque qu'il est composé de glace et d'eau liquide possède le même poids, c'est son volume qui est différent. Le poids du système reste le même, c'est la poussée d'Archimède qui varie selon l'état du système.
3. Étude du phénomène
Dans la suite, nous proposons un modèle pour déterminer les instants auxquels les gouttes se détachent du glaçon, puis nous montrons comment cela permet de réaliser une horloge précise sur une longue période.
3.1 Taille d'une goutte
Afin d'étudier la taille des gouttes relâchées, nous avons placé un glaçon coloré en bleu dans un bécher entre deux couches d'huiles de densité et de couleur différentes. Cela permet de simlpifier l'étude du phénomène, les oscillations du glaçon seront, dans ce cas, de plus petite amplitude que dans le cas du gradient de densité d'huile. Nous avons choisi pour l’huile du dessus une huile minérale de moteur, de masse volumique 850 kg/m3, et l’huile du dessous de l’huile de ricin, de masse volumique 960 kg/m3. Ces deux huiles sont non-miscibles. L’huile de ricin est plus légère que l’eau (de masse volumique d’environ 1 000 kg/m3), ainsi les gouttes qui se détachent du glaçon tombent directement au fond du récipient.
Sur la figure 5, on observe la première, deuxième, sixième et dixième goutte, après respectivement deux, trois, neuf et vingt minutes d'expérience. Ces gouttes ont toutes la même taille, de l'ordre du centimètre. En fait, cette taille est donnée par la longueur capillaire.
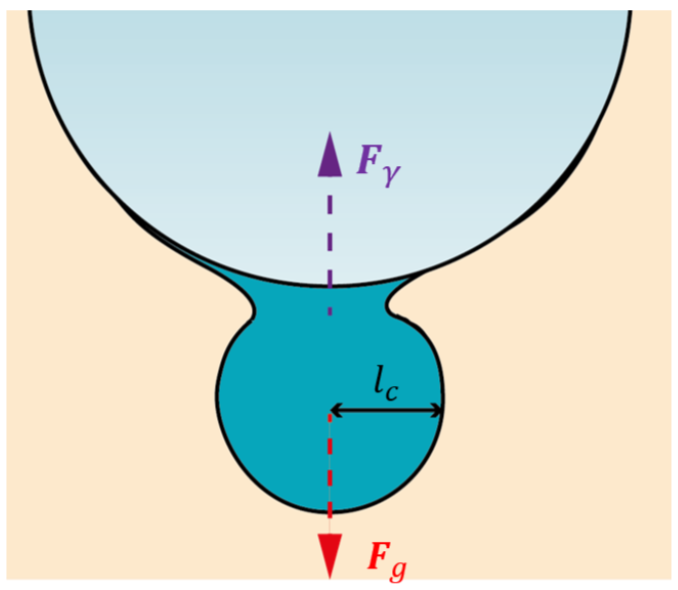
Lors de la formation d'une goutte, il y a une compétition entre deux phénomènes, comme on peut le voir en figure 6. La gravité tend à faire tomber la goutte, tandis que la tension superficielle tend à coller le film d'eau sur le glaçon.
Considérons une goutte sphérique de rayon \(l\) et de volume \(V_g\) (\(V_g\) = \( \frac{4}{3}\pi l^3\)).
Comme la goutte est immergée dans l'huile, la force due à la gravité n'est pas directement \(m_{g} \mathbf{g}\), car il faut prendre aussi en compte l'effet de la poussée d'Archimède. [On note ici en gras les grandeurs vectorielles]. En notant \(\rho_{eau~liquide}\) la masse volumique de l'eau et \(\rho_{b}\) la masse volumique de l'huile du bas, la force résultante est :
$$ \mathbf{F_g} = ( \Delta \rho V_g) \mathbf{g} $$
où \(\Delta \rho\) = \(\rho_{eau~liquide}\) - \(\rho_{b}\) est la masse volumique effective. On parle de gravité compensée.
La force résultante est donc proportionnelle à :
$$ \mathbf{F_g} \varpropto \Delta \rho l^3 \mathbf{g}~~~~\color{gray}{(eq1)} $$
D'autre part, la force due aux effets de tension superficielle est donnée en ordre de grandeur par :
$$ \mathbf{F_{\gamma}} \varpropto \gamma l~~~~\color{gray}{(eq2)} $$
où \(\gamma\) est le cœfficient de tension superficielle entre l'eau et l'huile de ricin.
En faisant le rapport entre ces deux termes et en négligeant tous les préfacteurs numériques, on définit alors la longueur capillaire \(l_c\) comme la taille pour laquelle ces deux forces se compensent :
$$ l_c = \sqrt{\frac{\gamma}{\Delta \rho g}}~~~~\color{gray}{(eq3)} $$
Ainsi, on s'attend à ce que la taille de goutte soit de l'ordre de la longueur capillaire.
Si la force de gravité est plus faible que la force de tension superficielle :
\( F_g < F_{\gamma} \), on a une goutte de rayon \( l < l_c = \sqrt{\frac{\gamma}{\Delta \rho g}} \) et la goutte ne tombe pas.
La goutte tombe lorsque la force de gravité devient plus grande que la force de tension superficielle :
\( F_g > F_{\gamma} \), on a : \( l > l_c \)
Le cœfficient de tension superficielle entre l'eau et l'huile du ricin vaut[1] \(\gamma\) ≈ 25 mN/m et la masse volumique effective \(\Delta \rho\) ≈ 40 kg/m3. On trouve alors une longueur capillaire de l'ordre de \(l_c\) ≈ 8 mm, ce qui est cohérent avec l'observation des gouttes de rayon de l'ordre du centimètre sur la figure 6.
3.2 Modification de la taille : tension superficielle
Nous avons vu que la taille des gouttes, donnée par la longueur capillaire, dépend notamment de la tension superficielle. Une façon simple de changer la tension superficielle entre l'eau et un autre milieu est d'ajouter des tensio-actifs (par exemple du savon), ce qui a pour effet de faire chuter la tension superficielle.
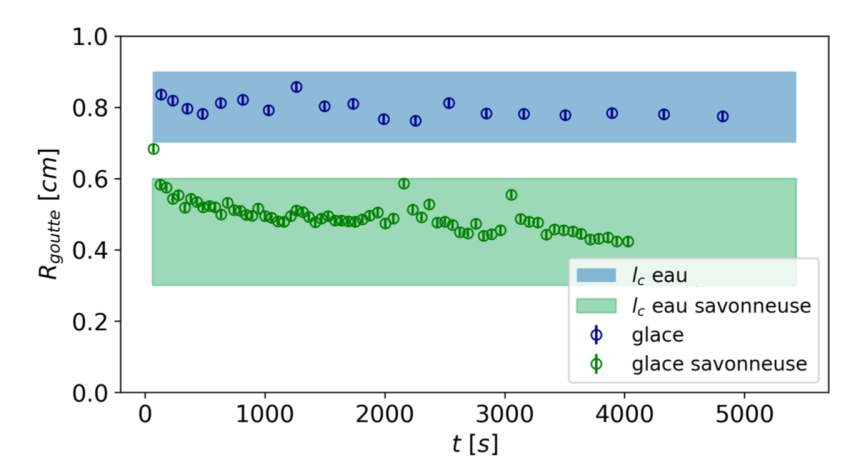
Sur la figure 7, on a tracé le rayon de chaque goutte en fonction du temps, pour un glaçon fait à partir d'eau (marqueurs φ bleus), et un glaçon fait à partir d'eau savonneuse (marqueurs φ verts). Les régions colorées correspondent à la longueur capillaire dans chacun des cas. Les bandes sont larges, car il est difficile[2] de mesurer avec précision le cœfficient \(\gamma\). On voit que la longueur capillaire prédit bien la taille des gouttes, et que changer le cœfficient de tension superficielle permet de la modifier.
4. Transferts thermiques : conduction, convection ou radiation ?
Maintenant que nous avons compris comment les gouttes se détachent du glaçon, il faut savoir comment celles-ci se forment, donc comprendre comment le glaçon fond. De façon générale, le transfert thermique peut se faire de trois façons différentes : conduction, convection ou radiation.
La contribution radiative, donnée par la loi de Stefan-Boltzmann, est négligeable devant les autres contributions. En fait, si l'on dispose des traceurs dans l'huile du dessous (ici des petits bouts de liège), on voit, figure 8, que ceux-ci sont entraînés dans des mouvements ascendants/descendants, mettant en évidence la présence de rouleaux de convection. On peut, de plus, montrer que la convection est le phénomène dominant en mesurant le gradient de température dans l'huile du dessous qui est de l'ordre de 1°C/cm ce qui fait qu'on peut négliger la conduction devant la convection.
On peut alors réaliser le bilan thermique sur le glaçon, en écrivant que la puissance thermique reçue par le glaçon \(P_{th}\) sert entièrement à sa fonte :
$$ P_{th} = \rho L_{fus} \displaystyle\left\lvert {\frac{dV}{dt}} \right\rvert = h S \Delta T~~~~\color{gray}{(eq4)} $$
où \(L_{fus}\) est la chaleur latente de fusion de la glace ou enthalpie de changement d'état, \(h\) le cœfficient de convection thermique, \(\Delta T\) ≈ 20°C la différence entre la température de l'huile loin du glaçon et la température du glaçon, et \(S\) et \(V\) la surface et volume du glaçon. En particulier la puissance surfacique :
$$ \frac{P_{th}}{S} = \frac{\rho L_{fus}}{S} \displaystyle\left\lvert {\frac{dV}{dt}} \right\rvert = h \Delta T~~~~\color{gray}{(eq5)} $$
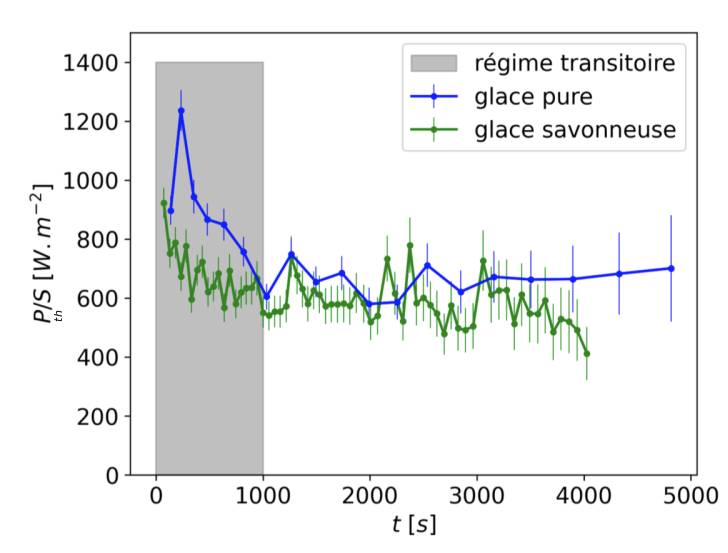
est constante en fonction du temps si l'huile ne se refroidit pas (ce qui est le cas quand le volume d'huile en dessous est grand par rapport à la taille du glaçon), comme on peut le voir sur la figure 9. On peut alors en déduire la valeur du cœfficient de convection thermique \(h\) ≈ 40 ± 5 Wm-2K-1, qui est indépendant de la tension superficielle.
5. L'horloge
5.1 Modélisation de l'horloge
Pour faire une horloge, il faut être capable de prédire les instants où les gouttes se détachent. Pour ce faire, on part du bilan thermique sur le glaçon (eq4), et l'on discrétise l'équation.
On note \(\Delta t_n\) l'intervalle de temps entre le détachement de la goutte \(n\) et la goutte \((n-1)\) et \(\Delta V\) la variation de volume de glaçon pendant ce temps. En supposant que sur cette courte durée la surface du glaçon reste constante égale à \(S_n\) (ce qui est une bonne approximation tant que le glaçon est beaucoup plus grand que la goutte), on peut réécrire l'équation (eq4) sous la forme :
$$ \rho L_{fus} \displaystyle\left\lvert {\frac{\Delta V} {\Delta t_n}}\right\rvert = h S_n \Delta T~~~~\color{gray}{(eq6)} $$
Or \(\Delta V\) = \(V_g\), ainsi :
$$ \Delta t_n = {\frac{\rho L_{fus} V_g}{h S_n \Delta T }}~~~~\color{gray}{(eq7)} $$
Dans le cas d'un glaçon sphérique de rayon \(R_n\), de volume \(V_n\) = \(\frac{4}{3}\pi R^3_n\) et de surface \(S_n\) = 4\(\pi R^2_n\), on trouve que \(S_n\) = \( (36 \pi)^{1/3} V^{2/3}_n \).
Or en toute généralité, le volume d'un glaçon après le détachement de \(n\) gouttes est \(V_n\) = \(V_0 - n V_g\), avec \(V_0\) le volume initial. Ainsi, on trouve que pour un glaçon sphérique :
$$ \Delta t_n = {\frac{\rho L_{fus} V_g}{h \Delta T (36 \pi)^{1/3} (V_0 - n V_g)^{2/3}}}~~~~\color{gray}{(eq8)} $$
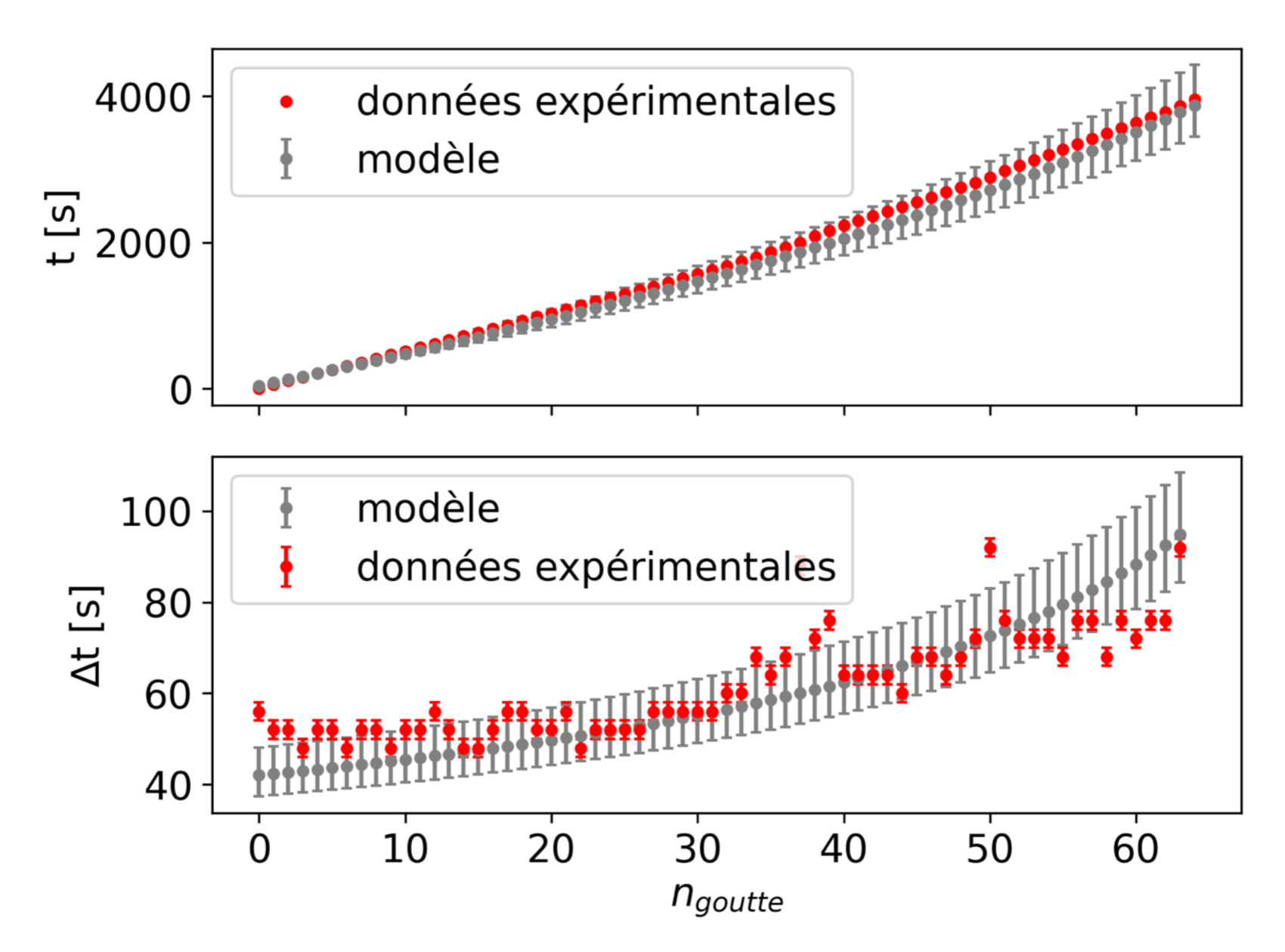
On peut voir, sur la figure 10, les instants de détachement de gouttes (en haut) et l'intervalle de temps entre deux gouttes (en bas). Les points rouges sont les données expérimentales, le faisceau gris correspond aux valeurs prédites par le modèle à l'incertitude sur le cœfficient de convection thermique près. Le modèle fonctionne relativement bien entre la 10e et la 50e goutte, à quelques imprécisions de mesure notamment sur les intervalles de temps entre deux gouttes. Le modèle semble alors corroborer avec les résultats expérimentaux dans le régime intermédiaire, en dehors du régime transitoire du départ et du régime où le glaçon et les gouttes sont de tailles similaires.
5.2 Amélioration de l'horloge
Dans le cas du glaçon sphérique, on observe un ralentissement du détachement des gouttes quand le volume du glaçon devient comparable à celui des gouttes. Ce ralentissement se manifeste car la surface d'échange entre le glaçon et l'huile diminue.
Pour minimiser cet effet, on peut prendre de gros glaçons, de sorte que la condition \( V_n \gg V_g \) reste valable plus longtemps.
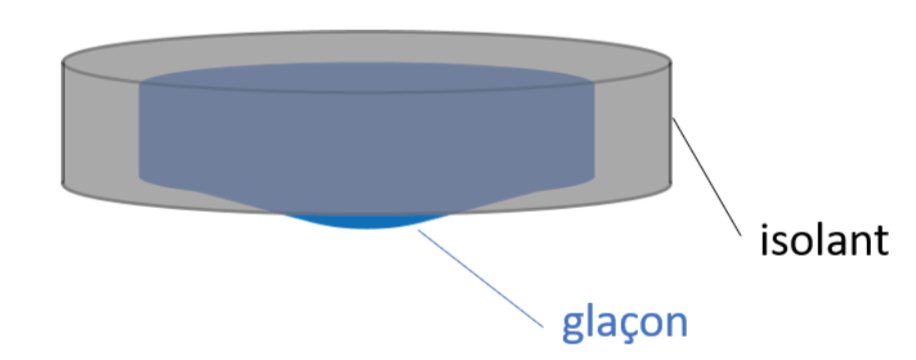
Mais pour faire une horloge avec une fréquence de détachements de gouttes constante, on voit en équation (eq7) qu'il faut avoir \( S_n \) constant. Pour cela, nous avons préparé un glaçon cylindrique, entouré par un isolant, de sorte que la surface en contact avec le liquide soit constante tout au long de l'expérience, figure 11.
De plus, comme on a \( \Delta t_n \varpropto \Delta T^{-1}\), il faut ainsi faire en sorte que la variation de température reste bien constante. Pour cela, il faut que les gouttes ne refroidissent pas (ou le moins possible) l'huile. Pour cela, nous avons travaillé avec un grand volume d'huile, et ajouté un volume d'eau sous l'huile du dessous, jouant le rôle de bain thermique.
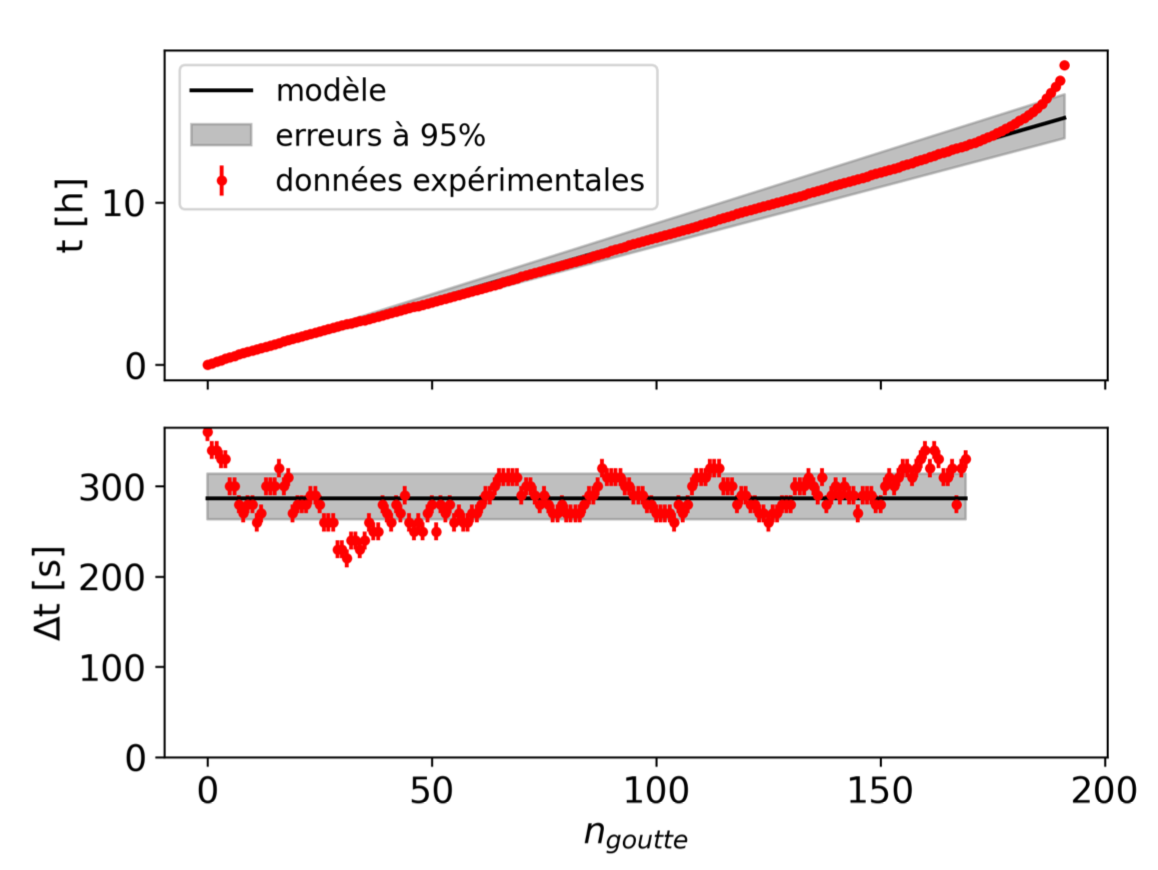
Un autre de nos objectifs était aussi de maximiser la durée de vie de l'horloge. Cette fois encore, il convient de prendre de gros glaçons et aussi de diminuer \( \Delta T\). Ainsi, nous avons réalisé notre dernière expérience dans un réfrigérateur tel que \( \Delta T\) = 7 K. Les résultats sont présentéss sur la figure 12. Comme dans le cas du glaçon sphérique, notre modèle explique bien les données expérimentales en dehors d'un régime transitoire sur les quelques premières gouttes et le régime où le détachement ralentit fortement sur les 20 dernières gouttes, car le glaçon devient petit et nous sortons de nos hypothèses. Entre les deux, on voit que la fréquence de détachement des gouttes oscille, à une fréquence qui correspond aux cycles de refroidissement du réfrigérateur. Néanmoins, on voit bien sur la figure du haut que nous avons été capable de réaliser une horloge ayant une relation nombre de gouttes-temps écoulé linéaire pendant plus de 10 heures.
Conclusion
Nous avons montré qu'un glaçon piégé entre deux huiles de densités différentes fond, et que du transfert convectif a lieu dans le récipient. Lorsque le glaçon fond, de l'eau s'accumule à sa base, formant une goutte qui se détache quand elle atteint une taille critique donnée par la longueur capillaire.
L'intervalle temps entre le détachement de deux gouttes successives est proportionnel au volume de la goutte (qui est contrôlé par la tension superficielle), et inversement proportionnel à la surface du glaçon et à la différence de température entre le glaçon et l'huile du dessous. En jouant sur ces paramètres, il est possible d'ajuster la fréquence de l'horloge ainsi que sa durée de vie.
En particulier, nous avons montré qu'il est possible de faire une horloge qui fonctionne pendant dix heures avec une fréquence de détachement constante.
Nous voulons remercier nos encadrants Nicolas Taberlet, Nicolas Plihon et Arsène Chemin pour leur aide et conseils durant nos expériences, ainsi que le reste de notre équipe (Roméo Beignon, Owen Chaffard, Julie Limonet et Solenn Rodriguez) pour nos discussions.
Références
Hydrodynamique physique, E. Guillon, L. Petit, J.-P. Hulin, Chapitre 1, p34, Interéditions
Vidéo du Ice clock problem
Pour citer cet article :
Comment faire une horloge avec un glaçon ?, Adria Rospars, Samuel Bera, octobre 2022. CultureSciences Physique - ISSN 2554-876X, https://culturesciencesphysique.ens-lyon.fr/ressource/ice-clock.xml