Activer le mode zen
Ressource au format PDF

Mots-clés

air poussée d'Archimède détente adiabatique refroidissement altitude atmosphère température pression

Froid en altitude

07/02/2007

Catherine Simand

Catherine Simand

Résumé

Une réponse à la question : Pourquoi, alors que l'air chaud monte, fait-il plus froid en montagne qu'à basse altitude ?

Table des matières

Pourquoi, alors que l'air chaud monte, fait-il plus froid en montagne qu'à basse altitude ?

Vue du Mont Blanc

Figure 1. Vue du Mont Blanc


Pour répondre à cette question, nous allons tout d'abord préciser quel va être notre objet d'étude. Ceux qui ont déjà étudié les mouvements des fluides savent que l'on utilise dès que cela est possible le modèle de particules de fluide. Une particule de fluide est un élément du fluide étudié, tel que sa taille soit à la fois très petite devant les échelles de longueur L caractéristiques de l'écoulement et très grande devant le libre parcours moyen ℓ des molécules. Pour un gaz, aux pressions usuelles, ℓ est de l'ordre d'un micromètre et est donc largement inférieur à L dans la plupart des cas. Le fluide est alors décrit comme un ensemble continu de particules de fluide, de volume V. A chacune d'entre elles, on associe différentes grandeurs physiques ou chimiques, comme par exemple une vitesse (moyenne des vitesses des molécules situées à l'intérieur de la particule de fluide, qui est de l'ordre de la vitesse du son), une température T, une pression P, une masse m, une masse volumique ρ = m / V , etc...

Le fluide qui nous intéresse ici est l'air, en mouvement dans l'atmosphère terrestre. L'atmosphère terrestre peut être découpée en fonction de l'altitude en différentes couches superposées. La troposphère, qui est la couche la plus basse, a une épaisseur moyenne de 11 km. L'enveloppe supérieure est la stratosphère, et entre les deux une couche d'air appelée tropopause forme la frontière supérieure de la troposphère. Pour des raisons qui apparaîtront par la suite, nous allons nous intéresser essentiellement à la troposphère, qui est également la zone d'intérêt des météorologues, puisque c'est dans cette couche qu'ont lieu la plupart des phénomènes météorologiques. Ce qui caractérise le plus simplement possible la troposphère est le profil vertical de température T(z), qui est justement ce que nous allons déterminer pour répondre à notre question.

Pour décrire l'évolution verticale des propriétés de la troposphère, les météorologues utilisent le plus souvent une échelle spatiale moyenne, l'échelle «aérologique», échelle correspondant à des particules d'air (ou parcelles d'air) dont les dimensions horizontales sont tout de même de l'ordre d'une cinquantaine de mètres !

L'air chaud monte...

Considérons une particule d'air, de volume V située à une altitude z, à une température T supérieure à la température T0 de l'air environnant. Cette particule d'air chaud a alors une masse volumique ρ inférieure à la masse volumique ρ0 de l'air autour d'elle. Elle est soumise à deux forces : son poids d'intensité ρ V g, orienté vers le bas, et la poussée d'Archimède d'intensité ρ0 V g, orientée vers le haut (g est l'accélération de la pesanteur). La résultante de ces forces est orientée vers le haut, et vaut (ρ0 - ρ) V g. Cet air chaud va donc monter, comme une mongolfière remplie d'air chaud monte dans l'air froid qui l'environne. Durant le même temps, de l'air froid situé au dessus, plus lourd, va descendre. Ces mouvements constituent la convection thermique.

Cependant, à la différence d'un ballon sonde ou d'une mongolfière, la pression et la masse volumique de la particule d'air vont varier avec l'altitude. L'équilibre des pressions entre la particule d'air et l'air environnant est pratiquement immédiat (il se réalise typiquement à la vitesse du son dans l'air ). Or la pression atmosphérique diminue avec l'altitude. Lorsque une particule d'air, initiallement située à une altitude z, à la pression P, passe à une altitude supérieure z + dz, sa pression diminue et prend la valeur P + dP, où dP < 0. Elle va donc se détendre, sa masse volumique ρ va également diminuer. Cette détente s'accompagne forcément d'une modification de la température T de la particule d'air. De sorte que l'évolution de la température T de l'air en fonction de l'altitude z est liée aux évolutions de la pression atmosphérique P(z) et de la masse volumique ρ(z).

Nous allons donc nous intéresser ici uniquement aux variations verticales de la température T, la pression P et la masse volumique de l'air ρ. La pression atmosphérique en particulier ne dépendra que de l'altitude z. Pour déterminer ces trois inconnues T(z), P(z) et ρ(z), il nous faut trois équations.

Les équations du problème

L'équation de l'hydrostatique

Cette équation traduit simplement l'équilibre mécanique d'une particule d'air, située entre les altitudes z et z + dz, et de surface horizontale S. Elle subit :

  • une force de pression exercée par l'air situé en-dessous, à la pression P, de norme P . S ;
  • une force de pression exercée par l'air situé au-dessus, à la pression P + dP, de norme (P + dP) . S ;
  • des forces de pression exercées par l'air situé sur les côtés, qui s'annulent toutes deux à deux ;
  • l'attraction terrestre (le poids) de norme égale à ρ g S dz.

A l'équilibre, la somme vectorielle des forces qui s'exercent sur la particule d'air est nulle. On en déduit : dP = - ρ g dz, soit :

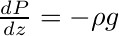
On vérifie que P diminue quand z augmente.

L'air : un gaz parfait

L'équation d'état des gaz parfaits relient les trois grandeurs P, T et ρ de la façon suivante : P = ρ RT / M, où R est la constante des gaz parfaits et vaut R = 8, 314 J. mol-1 . K-1 et M est la masse molaire du gaz considéré (M = 29 g . mol-1 pour l'air sec).

En météorologie, la précision du modèle des gaz parfaits est suffisante pour qu'il soit appliqué à l'air sec mais également à la vapeur d'eau, donc à l'air humide. Soit une particule fluide d'air humide, de masse m, de volume V, à la pression atmosphérique P, et pairsec et peau les pressions partielles de l'air sec et de la vapeur d'eau, telles que P = pairsec + peau.

Pour l'air sec, de masse mairsec : pairsec V = mairsec R T /Mairsec et pour la vapeur d'eau, de masse meau : peau V = meau R T / Meau, avec m = mairsec + meau. Alors il vient :

P V = pairsec V + peau V = mairsec R T /Mairsec + meau R T / Meau= m (mairsec / (m Mairsec) + meau / (m Meau) ) R T. On peut alors facilement mettre cette expression sous la forme P = ρ RT / M, où M est ici un coefficient qui dépend des masses molaires Mairsec et Meau et du rapport de mélange r = meau / mairsec lié au taux d'humidité de l'air.

On obtient alors pour l'air sec ou pour l'air humide la relation suivante :

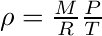
En remplaçant ρ dans l'équation de l'hydrostatique, on obtient l'équation différentielle :

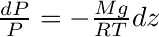
que nous allons intégrer entre l'altitude z0 et l'altitude z, en considérant que g est constante sur l'ensemble des altitudes considérées.

L'atmosphère isotherme

Le cas le plus simple est celui où la température reste constante avec l'altitude. Ceci n'est pas vrai dans la troposphère, mais c'est pratiquement le cas dans la tropopause. L'intégration de l'équation précédente conduit à l'évolution suivante pour la pression :

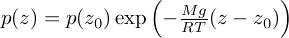
et à une évolution similaire pour la masse volumique :

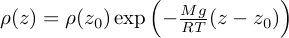
Physiquement, cette situation correspond à un cas limite d'homogénéisation infiniment rapide de l'atmosphère en température.

Modèle d'une évolution adiabatique

L'atmosphère adiabatique

Dans la troposphère, les transferts thermiques se font au contraire se façon très lente, en lien avec la faible conduction de l'air. Il n'y a quasiment pas de transferts thermiques entre la particule d'air, montant ou descendant, et l'air qui l'entoure. Ces déplacements convectifs peuvent être considérés en première approximation comme s'effectuant de manière adiabatique.

La durée Δt correspondant au phénomène de conduction thermique sur une échelle spatiale L vaut typiquement L2/K, où K est la diffusivité thermique du milieu considéré. Pour l'air, à 15°C, K vaut environ 2×10-5 m2.s-1 ; ce qui pour L = 10 m conduit à Δt = 58 jours !

Pour un gaz parfait, une transformation adiabatique réversible se traduit par des relations dites de Laplace dont celle-ci entre P et ρ : P ρ-γ = Cte. D'où on déduit :

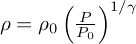où γ est le rapport Cp/Cv des capacités thermiques de l'air, et ρ0 et P0 sont la masse volumique et la pression en z0.

Cette relation n'est valable que dans un domaine où le coefficient γ est indépendant de la température. Pour toute la gamme de températures de la troposphère, nous allons considérer que γ est constant, et vaut γ = 7/5 = 1,4, valeur habituellement utilisée pour les gaz diatomiques,comme l'air.

Les évolutions de la pression, de la masse volumique et de la température

En remplaçant ρ dans l'équation de l'hydrostatique, on obtient l'équation différentielle suivante :

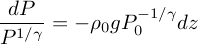que l'on intègre entre l'altitude z0 et z.

Nous obtenons après intégration :

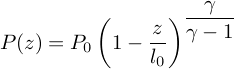
où 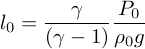est une longueur caractéristique.

On en déduit alors les évolutions suivantes pour la masse volumique et la température :

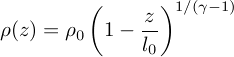et

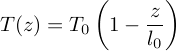
C'est à dire une décroissance linéaire de la température en fonction de l'altitude.

Le gradient de température

Usuellement, les météorologues appelle gradient de température la composante selon la verticale ascendante du vecteur grad(T).

Pour l'air sec, en prenant γ = 1,40 ; g = 9,81 m.s-2 ; ρ0 = 1,23 kg.m-3 ; et P0 = 1,013 bar = 1,013×105 Pa, on obtient l0 = 29,4 km. De sorte que le gradient thermique vertical vaut si T0 = 15°C : - T0/l0 = - 9,8×10-3 K.m-1. Cette valeur est celle du gradient adiabatique sec, voisin donc de - 10°C par km.

En réalité, l'air atmosphérique est humide. Quelle est l'influence de cette humidité ? En se refroidissant, la vapeur d'eau contenue dans l'air humide se condense. Cette liquéfaction est exothermique. Le transfert thermique libéré entraîne un échauffement de la masse d'air. De sorte que la valeur absolue du gradient vertical de température est plus faible que pour l'air sec. En moyenne, le gradient adiabatique saturé est estimé à -6,5°C par km.

La décroissance verticale linéaire de la température avec l'altitude est la caractéristique physique majeure de la troposphère. On l'observe sur une épaisseur moyenne de 11 km. Il y a toutefois des exceptions, avec des couches d'inversion de température, le plus souvent brèves ou limitées à des régions bien identifiées.

L'épaisseur de la troposphère est variable selon la latitude et les saisons : d'environ 8 km aux pôles, elle peut atteindre 15 à 20 km à l'équateur.

Au dessus de la troposphère, la température varie moins avec l'altitude, voire augmente. Par exemple, la composition de l'air dans la stratosphère (notamment la présence d'ozone...) permet une absorption du rayonnement solaire, donc un réchauffement.

Stabilité de la troposphère

Si la norme du gradient thermique est supérieure à celle du gradient adiabatique saturé

Une masse d'air qui s'élève se refroidit selon le gradient adiabatique saturé correspondant à son taux d'humidité. Sa température après détente est alors supérieure à la température de l'air qui l'entoure, qui est liée au gradient thermique réel. Sa masse volumique est donc plus faible que celle de l'air environnant : elle continue à monter sous l'effet de la poussée d'Archimède.

Inversement, une masse d'air qui descend, se réchauffe, mais pas suffisamment pour être en équilibre avec l'air ambiant qu'elle traverse : elle est plus froide que l'air environnant et continue à descendre.

Dans ce cas, les mouvements verticaux sont donc amplifiés : l'atmosphère est instable. Les particules polluantes contenues dans l'air sont soit projetées au sol, soit envoyées en altitude : la visibilité est bonne.

Si la norme du gradient thermique est inférieure à celle du gradient adiabatique saturé

Les mécanismes sont tous inversés. Par exemple, une masse d'air qui s'élève se refroidit plus vite que l'air autour d'elle : elle va redescendre. Les différentes masses d'air se déplacent peu verticalement, l'atmosphère est stable. Les polluants et les poussières restent en suspension dans l'air, la visibilité est faible.

Pour aller plus loin

Pour citer cet article :

Froid en altitude, Catherine Simand, février 2007. CultureSciences Physique - ISSN 2554-876X, https://culturesciencesphysique.ens-lyon.fr/ressource/QSfroidenaltitudeSol.xml

Ressource au format PDF