Archimède dans l'air

Notre ballon de baudruche n'a pas la forme d'une sphère (on peut en trouver sur le marché qui ont cette propriété) mais on peut envisager une première approximation en utilisant le calcul du volume d'une sphère en choisissant, pour le rayon, la moyenne des demi-longueurs des "diamètres" du ballon.

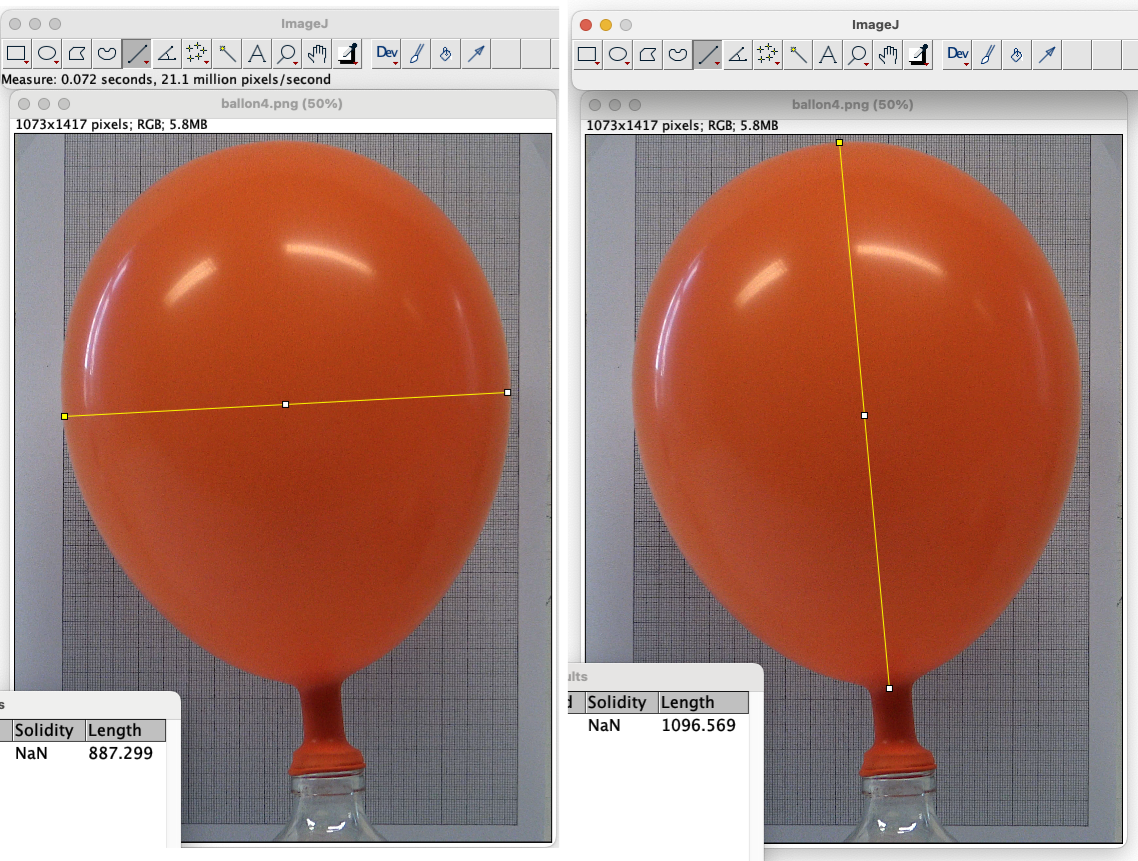
À l'aide de l'image du ballon prise devant une feuille de papier millimétré et du logiciel de traitement d'images ImageJ [2], figure 4, on peut mesurer ces deux "diamètres". Pour cela, on se sert de la feuille de papier millimétré pour définir l'échelle correspondante entre pixel et cm. Puis avec l'outil ligne droite et le menu Analyze puis Measurement, on a accès à la longueur sélectionnée en pixel.

Figure 4.  Mesure des deux "diamètres" du ballon

On trouve :

\( D_{largeur} \approx\) 887 px ± 5 px et \( D_{longueur} \approx\) 1096 px ± 5 px

Avec la conversion pixel/cm, grâce à la feuille de papier millimétré, on trouve : 1 pixel ≈ 0,0197 cm

\( D_{moy} =\frac{D_{longueur}+D_{largeur}}{2}\) d'où \( r_{moy} \approx\) 9,76 ± 0,098 cm

Le volume estimé d'air est \(V_{air} = \frac{4}{3} \pi r_{moy}^3= \) 3 901 ± 118 cm³

On obtient, pour la masse volumique de l'air :

\( \rho_{air_1} = \frac{\Delta m}{V_{air}} =\) 0,922 ± 0,052 kg.m^-3

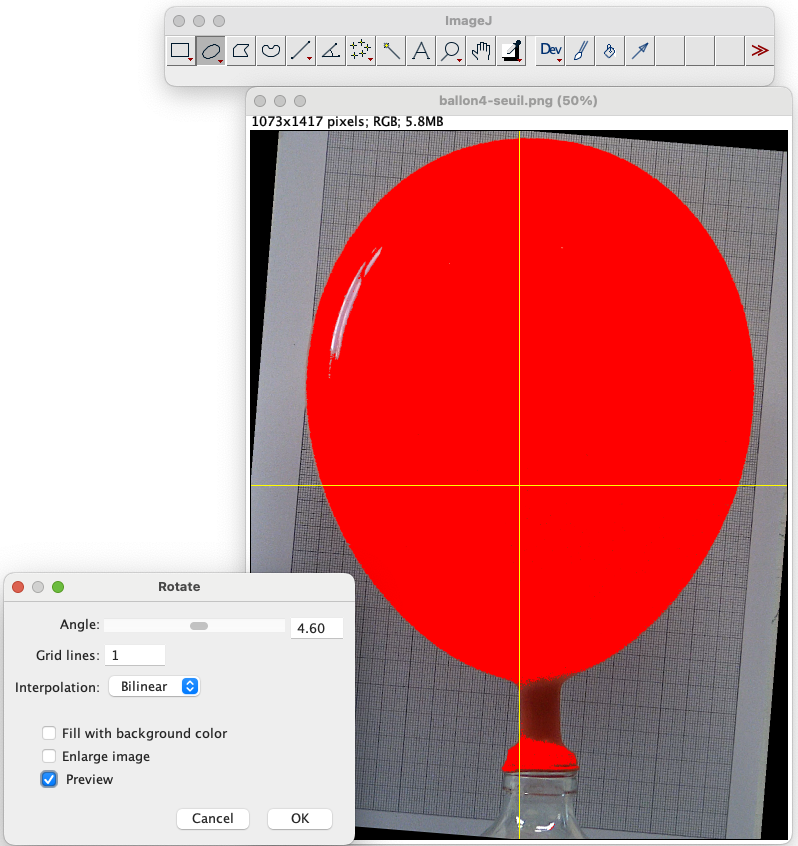
Dans cette partie nous allons remonter à l'estimation du volume du ballon en l'assimillant à un empilement de "tranches" de ballon, semblables à des cylindres. À l'aide de l'image du ballon et du logiciel de traitement d'images ImageJ [2], on va mettre en évidence les pixels qui correspondent à l'image du ballon. Pour cela, dans le menu Image, on sélectionne Adjust → Treshold Color, figure 5.

On effectue une petite rotation de l'image pour avoir le ballon "droit", à l'aide du menu Image, on sélectionne Transform → Rotate, figure 6.

Figure 5.  Seuillage de l'image pour déterminer les pixels appartenants au ballon

Figure 6.  Rotation de l'image du ballon

On sélectionne la partie de l'image qui contient le ballon, à l'aide de l'outil Selection, figure 7 puis Crop, figure 8.

Figure 7.  Selection d'une zone de l'image autour du ballon

Figure 8.  Rognage de l'image autour du ballon

Puis, à l'aide de l'outil Wand (Baguette magique) on clique sur le ballon et son contour vient se dessiner en jaune, figure 9.

À partir du contour du ballon, nous allons créer un masque à l'aide du menu Edit → Selection → Create Mask. Une image en noir et blanc se crée, correspondant à l'image du ballon, figure 10.

Figure 9.  Sélection du ballon par la baguette magique

Figure 10.  Masque de l'image du ballon

Maintenant, on exporte cette image vers un tableur, à l'aide du menu File → Save as → Text image.

L'image est binarisée : tout ce qui est noir correspond à "0" et tout ce qui est blanc à la valeur "255". L'image du masque mesure 926 x 1120 pixels. Ainsi, lorsqu'on l'ouvre dans un tableur, une matrice de 926 colonnes par 1120 lignes s'affiche.

Il suffit maintenant de repérer la couleur blanche correspondant au ballon, donc les valeurs "255". Le ballon est vu comme un solide de révolution, ainsi, on va calculer son volume "tranche" par "tranche", où une "tranche" d'épaisseur un pixel peut être vue comme un cylindre de section circulaire, de hauteur 1 pixel, et de diamètre le nombre de pixels à la valeur "255". Pour trouver ce nombre de pixels, on se sert de la fonction NB.SI(plage;critere) qui vient compter le nombre de fois que le critère est atteint : "255" sur la plage correspondant à une ligne.

En guise d'illustration, la figure 11 présente un extrait du tableau de valeurs codant le ballon. Sur la dernière colonne (AIR) on réalise le calcul du nombre de pixels correspondant au ballon. Pour la ligne 1, cela s'écrit : =NB.SI(A1:AIP1;"255"). On ne trouve, pour cette ligne, aucune occurence, c'est en effet ce que l'on retrouve figure 12, sur les pixels correspondants de l'image.

Figure 11.  Extrait du tableau de valeurs codant l'image du masque du ballon

Figure 12.  Sélection en jaune représentant les 50 premiers pixels du haut de l'image du ballon

En se servant de l'image du papier millimétré, on peut remonter à la correspondance pixel/cm : 1 pixel ≈ 0,0197 cm

Ensuite, pour chaque ligne, on calcule le volume correspondant à cette "tranche" de ballon, en utilisant la formule du volume d'un cylindre.

Le volume total du ballon, mesuré de cette façon, est alors la somme de toutes les "tranches" du ballon d'où la somme des volumes calculés pour chaque ligne du tableur. On trouve : volume = 3 374 ± 59 cm³

On obtient alors, pour la masse volumique de l'air :

\( \rho_{air_{2}} = \frac{\Delta m}{volume}\) = 1,066 ± 0,047 kg.m^-3

On va venir immerger le ballon dans un contenant rempli préalablement par de l'eau. On récupère le volume d'eau déplacé dans un autre récipient (qui englobe le premier), il correspond approximativement au volume du ballon, figure 13.

On mesure le volume d'eau recueilli dans la bassine blanche.

On trouve : \( volume_{eau} \approx\) 2 657 ± 100 mL ou 2 657 ± 100 cm³

On obtient alors, pour la masse volumique de l'air :

\( \rho_{air_3} = \frac{\Delta m}{volume_{eau}} =\) 1,317 ± 0,85 kg.m^-3

Le tableau 1 récapitule les valeurs des volumes mesurés et des masses volumiques obtenues.

La valeur tabulée pour de l'air à 19°C est \( \rho_{air_{tab}} =\)1,203 ± 0,003 kg.m^-3 (pour un pourcentage d'humidité entre 20% et 80%) [3].

On observe que la première méthode sous-estime la valeur de la masse volumique de l'air car la mesure du volume du ballon est sur-estimée. En effet, la moyenne des deux "diamètres" du ballon représente une sphère plus grande que le volume réel du ballon, figure 14. Néanmoins elle présente l'avantage d'arriver à l'ordre de grandeur de la masse volumique de l'air, très rapidement, sans trop de calculs.

La deuxième méthode semble donner une valeur plus proche de la valeur tabulée en la sous-estimant encore. On peut citer, comme limitation, le fait que la feuille de papier millimétré se trouve derrière le ballon, on a alors un biais sur la mesure des dimensions du ballon.

La troisième méthode a contrario sous-estime le volume d'air dans le ballon. La manipulation est difficilement précise et de l'eau a giclé en dehors du récipient blanc. De plus le ballon est aussi un peu déformé dans le récipient rempli d'eau, la pression exercée par l'eau n'est pas la même que celle exercée dans l'air. Cette expérience a aussi été réalisée plus tard (environ 30 minutes), et nous avons pu observer que le ballon utilisé est assez poreux.

Figure 14.  Cercle de diamètre estimé par la moyenne des deux longueurs, verticales et horizontales, du ballon

Finalement, cette expérience assez simple et originale met en évidence l'effet de la poussée d'Archimède et permet de tester toute une palette d'outils pour remonter à la valeur de la masse volumique de l'air.