Activer le mode zen
Ressource au format PDF
Classification
Observations de l'effet Leidenfrost
13/05/2024
Travail réalisé dans le cadre des Olympiades de Physique, encadré par les enseignants Jean-Brice Meyer et Tristan Clément.
Table des matières
Introduction
Nous sommes une équipe de 4 élèves de Terminale, passionnés de physique, et nous avons eu la volonté de nous investir dans un projet scientifique. L'effet Leidenfrost a plus particulièrement retenu notre attention. Nous avons alors voulu comprendre ce phénomène en menant une démarche d'investigation la plus personnelle possible. Comme nous ne partions de rien en termes de connaissances ou encore d'observations, nous avons commencé par réaliser différentes expériences, sans objectifs particuliers si ce n'est, dans un premier temps, se faire une vague idée des paramètres qui interviennent dans le phénomène étudié. Puis, nous avons été particulièrement intrigués par un « triple » effet Leidenfrost.
1. Observations d'une goutte d'eau sur une plaque chaude
1.1 Dispositif expérimental
Le matériel nécessaire est très simple, il suffit d'une plaque chauffante et d'une pipette pour déposer des gouttes.
On réalise l'expérience en faisant varier la température de la plaque et on remarque que pour certaines gammes de température, le comportement des gouttes d'eau est étonnant : les gouttes ruissellent sur la plaque. C'est cet effet que l'on nomme « effet Leidenfrost », figure 1.
Figure 1. Mise en évidence de l'effet Leidenfrost sur une plaque chauffante Source : Clara Carlin, Gabriel Soleil, Naomie Viaud et Alexandre Dauger. |
L'explication de cet effet est connue : cela s'explique par le fait que lorsque la goutte s'approche de la plaque, une partie de l'eau qui la compose, en particulier la partie du dessous, s'évapore, ce qui produit une couche de vapeur d'eau qui empêche la goutte d'entrer en contact avec la plaque chauffante. La goutte est alors en lévitation sur la plaque, et peut s'écouler sans se mettre à bouillir, figure 2.
Figure 2. Illustration de l'effet Leidenfrost
Source : Mononoke~commonswiki, Wikimedia.
Comme justement les gouttes s'écoulaient sur la plaque, nous avons décidé d'observer cet effet en versant des gouttes dans une coupelle déposée sur la plaque chauffante, figure 3.
Figure 3. Mise en évidence de l'effet Leidenfrost dans une coupelle chauffée Source : Clara Carlin, Gabriel Soleil, Naomie Viaud et Alexandre Dauger. |
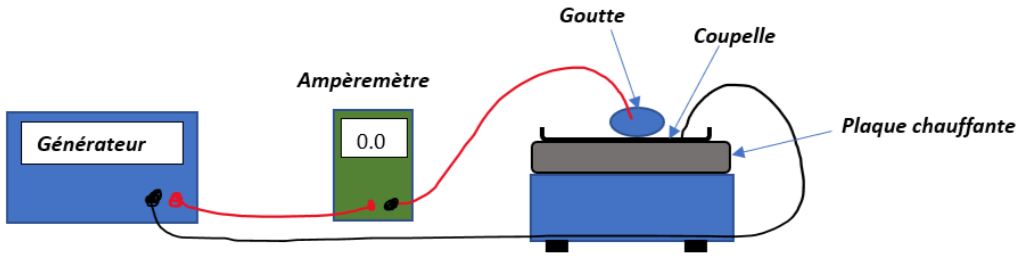
Nous avons souhaité nous assurer que la goutte d'eau est bien en lévitation sur la surface chaude, et donc qu'elle n'est pas en contact avec la surface chauffée. Pour ce faire, nous avons réalisé un circuit électrique simple comprenant, en série, un générateur, un ampermètre, la goutte et la coupelle, figure 4.
Figure 4. Mise en évidence de la lévitation de la goutte Source : Clara Carlin, Gabriel Soleil, Naomie Viaud et Alexandre Dauger. |
La mesure montre qu'aucun courant ne circule dans le circuit, la coupelle et la goutte ne sont pas en contact. Cela confirme que la goutte est bien en lévitation au-dessus de la coupelle.
Lors de nos différents essais, nous avons remarqué que le phénomène était en réalité plus capricieux qu'on ne l'imaginait, l'effet Leidenfrost s'observe, en effet, pour des températures de plaque et des volumes de gouttes bien particuliers.
1.2 Vibration de la goutte
Pamri toutes nos observations, il nous est aussi arrivé de voir que la goutte déposée sur la plaque change de forme au cours du temps : elle se met à vibrer et présente une géométrie avec une base carrée ou même hexagonale, figures 5 et 6.
Figure 5. Différentes formes de goutte observées Source : Clara Carlin, Gabriel Soleil, Naomie Viaud et Alexandre Dauger. |
Figure 6. Vibration de la goutte et modification de sa géométrie Source : Clara Carlin, Gabriel Soleil, Naomie Viaud et Alexandre Dauger. |
1.3 Dépot de plusieurs gouttes simultanément sur la plaque
Nous avons aussi essayé de verser plusieurs gouttes sur la plaque.
Si les gouttes déposées sont deux gouttes du même liquide, nous avons remarqué qu'elles coalescent dès qu'elles se rencontrent, figure 7.
Figure 7. Coalescence de deux gouttes d'eau Source : Clara Carlin, Gabriel Soleil, Naomie Viaud et Alexandre Dauger. |
Nous avons aussi versé sur la plaque des gouttes de différents liquides, et dans ce cas particulier, le résultat était assez spectaculaire, vidéo figure 8. On peut voir que la goutte d'eau colorée en rouge (pour reconnaître la goutte d'eau) et celle d'acétone ne coalescent pas lors de leur rencontre, alors que ces deux liquides sont miscibles. Mieux que cela, on peut observer qu'au bout d'un certain temps, ces gouttes coalescent ! Comment expliquer cela ?
Figure 8. Deux liquides miscibles qui ne coalescent pas (eau colorée et acétone) Source : Clara Carlin, Gabriel Soleil, Naomie Viaud et Alexandre Dauger. |
1.4 Modification du matériel
Lors de nos essais, nous avons remarqué que si l'on versait plusieurs gouttes d'eau successivement sur la coupelle, il était impossible d'observer l'effet Leidenfrost. Après discussion avec monsieur Moreau (maître de conférence ENSMA institut Pprime – Poitiers), nous avons pensé que la succession de gouttes d'eau diminuait la température de la coupelle, ce qui empêchait alors l'apparition du phénomène étudié (la coupelle étant en effet assez fine : environ 1 mm d'épaisseur).
Nous avons tenté une approche pour évaluer l'épaisseur de la plaque nécessaire pour observer l'effet Leidenfrost. Pour cela nous avons fait les hypothèses suivantes :
- l'énergie thermique transférée par la plaque à la goutte est intégralement utilisée pour vaporiser le liquide,
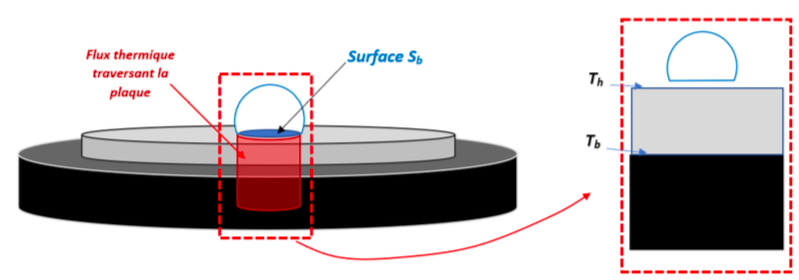
- le transfert thermique entre la plaque et la goutte se fait uniquement sur une surface correspondant à la surface Sb de la base de la goutte (voir figure 9).
Avec ces hypothèses, en appelant \( D_m \) le débit massique de liquide évaporé, on peut écrire que l'énergie thermique \( Q \) échangée entre la plaque et la goutte, à une date t, est égale à :
$$ Q = m L_v $$
où \( L_v \) est la chaleur massique de vaporisation du liquide et \( m \) la masse évaporée à la date t. On a :
$$ \frac{dQ}{dt} = \frac{dm}{dt} L_v = D_m L_v = \Phi $$
où \(\Phi \) est le flux thermique.
En appliquant la loi de Fourier pour la conduction thermique à la plaque, on peut exprimer \( \Phi \) :
$$ \Phi = \frac{T_h - T_b}{R_{th}} $$
où \(R_{th} =\frac{e}{\lambda S_b}\) est la résistance thermique de la plaque avec \(e \) l'épaisseur de la plaque et \(\lambda \) la conductivité thermique de la plaque.
On en déduit alors l'expression suivante :
$$ D_m L_v = \frac{ (T_h - T_b) \lambda S_b}{e} $$
Autrement dit, pour une plaque de matériau de conductivité thermique connue, la plaque doit avoir une épaisseur :
$$ e = \frac{ (T_h - T_b) \lambda S_b}{D_m L_v} $$
Nous avons pu évaluer quantitativement la valeur de l'épaisseur grâce à quelques mesures du débit massique et des caractéristiques géométriques des gouttes réalisées et présentées dans la section 2, et après avoir mesuré les températures sur et sous une plaque en aluminium, on trouve :
$$ e = \frac{ 22 \times 226 \times 32.10^{-6}}{1,75.10^{-6} \times 2,25.10^{-6}} \approx 4~cm $$
Source : Clara Carlin, Gabriel Soleil, Naomie Viaud et Alexandre Dauger. |
Nous nous sommes alors procuré une plaque plus épaisse qui présente en plus l'avantage d'être très légèrement incurvée de sorte que la goutte d'eau reste au centre de la plaque, figure 10.
Notre plaque ne mesure pas 4 cm d’épaisseur, mais l’ordre de grandeur est très bon. On peut comprendre la différence entre le modèle et la réalité car dans les faits, la conduction thermique ne se fait pas uniquement depuis le bas de la plaque vers la surface du haut, mais elle se fait également depuis les côtés. La plaque n’a donc pas besoin d’être aussi épaisse que le suggère le modèle établi.
Figure 10. Plaque incurvée déposée sur la plaque chauffante Source : Clara Carlin, Gabriel Soleil, Naomie Viaud et Alexandre Dauger. |
2. Quelles sont les conséquences de l'effet Leidenfrost sur l'évolution de la goutte d'eau ?
2.1 Évaporation de la goutte en fonction de son volume initial
Nous avons tout d'abord voulu savoir si la façon dont s'évapore la goutte dépendait de son volume initial.
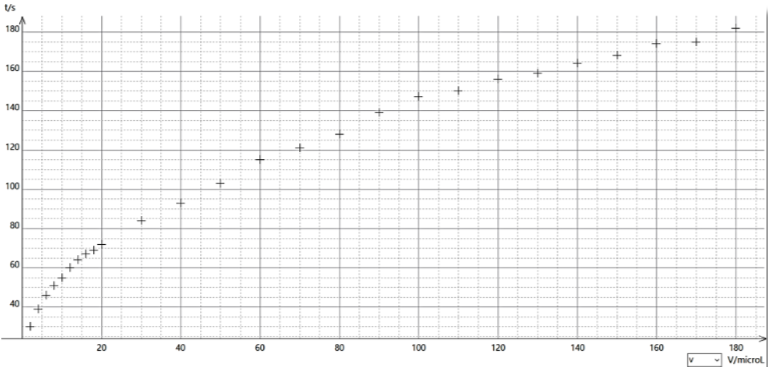
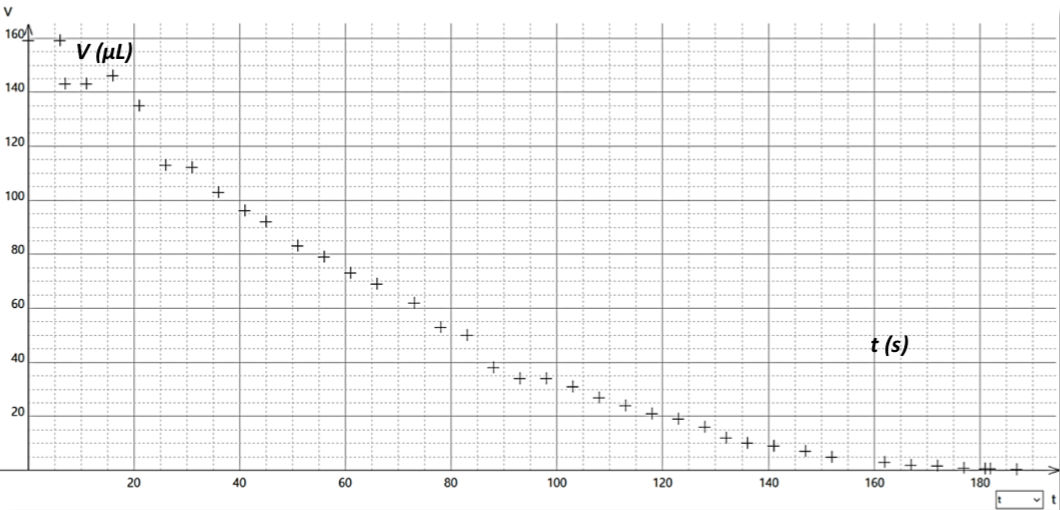
Pour ce faire, nous déposons une goutte d'un certain volume sur la plaque et nous mesurons son temps de vie, du premier contact de la goutte sur la plaque jusqu'à son évaporation complète. Nous travaillons avec une température fixe sur une plage comprise entre 280°C et 300°C et avec des gouttes dont nous avons fait varier le volume de 2 μL à 200 μL, figure 11.
Figure 11. Durée de vie de la goutte en fonction de son volume initial Source : Clara Carlin, Gabriel Soleil, Naomie Viaud et Alexandre Dauger. |
Les résultats montrent que pour de faibles volumes de gouttes, inférieurs à environ 20 μL, une variation du volume de la goutte a une plus grande influence sur sa durée de vie que pour une goutte dont le volume initial est supérieur à 20 μL. En fait, le graphique met en évidence deux régimes de part et d'autre de 20 μL. Pourquoi y a-t-il deux évolutions différentes ?
En observant des gouttes de différents volumes, il apparaît que pour des volumes inférieurs à environ 20 μL, les gouttes paraissent sphériques, alors qu'au-dessus de ce volume, elles ont une forme aplatie. On peut l'observer, par exemple sur la figure 12, pour ces deux gouttes dont le volume est pour l'une très inférieur à 20 μL, et pour l'autre très supérieur à 20 μL.
Figure 12. Forme de deux gouttes de volume différent : à gauche 4 μL et à droite 125 μL Source : Clara Carlin, Gabriel Soleil, Naomie Viaud et Alexandre Dauger. |
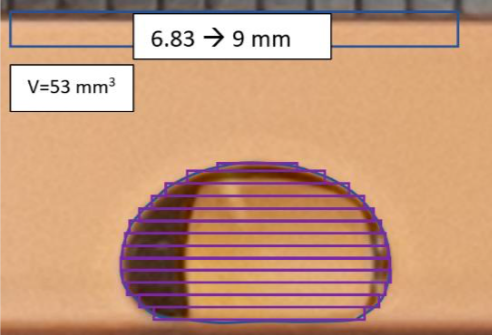
Afin de suivre l'évolution du volume d'une goutte au cours du temps, nous avons déposé une goutte unique de 200 μL sur la plaque et nous avons pris des photos de la goutte de profil, toutes les 5 secondes, jusqu'à son évaporation. Une première méthode a consisté à analyser chaque photo prise pour mesurer le volume en découpant la goutte en tranches, comme le montre la figure 13.
Figure 13. Mesure du volume d'une goutte en découpant la goutte "en tranches cylindriques" Source : Clara Carlin, Gabriel Soleil, Naomie Viaud et Alexandre Dauger. |
En utilisant l'échelle de la photo et la formule du volume du cylindre (\(V = \pi r^2 h \)), il nous suffisait alors d'ajouter tous les volumes des tranches cylindriques pour trouver celui de la goutte. Cette étape a été longue, car nous avons réalisé ces mesures toutes les 5 secondes, pendant 3 minutes.
Nous avons pu, dans un deuxième temps, utiliser une autre méthode qui a consisté, à partir du profil de la goutte pris toutes les 5 secondes, à reconstituer la forme de la goutte en 3 dimensions grâce au logiciel Fusion 360, figure 14. L'avantage de cette méthode est que nous pouvions alors, suite à cette modélisation 3D, obtenir toutes les caractéristiques géométriques de la goutte au cours du temps, et en particulier, son volume et sa surface réelle. Ceci s'est avéré vraiment très intéressant pour les études menées par la suite.
Figure 14. Capture d'écran issue de la modélisation 3D de la goutte d'eau à une date donnée Source : Clara Carlin, Gabriel Soleil, Naomie Viaud et Alexandre Dauger. |
L'utilisation du logiciel de modélisation de la goutte est présenté dans cette vidéo sur la mesure du volume de la goutte.
Ainsi, connaissant le volume de la goutte, nous avons pu calculer la surface théorique que la goutte aurait eu si elle avait été sphérique, et nous avons comparé cette surface théorique à la surface réelle donnée par la modélisation 3D. Sur le graphique figure 15, on représente alors l'écart (\(E \)) entre ces deux surfaces, en fonction du rayon théorique de la goutte sphérique. On voit clairement que si on choisit un critère de 2 mm2 concernant cet écart, le passage de la goutte sphérique à aplatie se fait pour des gouttes de rayon 1,7 mm, soit un volume de 20 μL.
Source : Clara Carlin, Gabriel Soleil, Naomie Viaud et Alexandre Dauger. |
En cherchant à confronter nos résultats à ceux que l'on peut trouver dans la littérature, nous avons vu que la dimension de la goutte limite entre une goutte sphérique et une goutte aplatie correspondait à la « longueur capillaire » donnée par :
$$ l_C = \sqrt{ \frac{ \gamma}{\rho g} } $$
où \(\gamma\) est la tension superficielle et \(\rho\) la masse volumique du liquide.
Pour de l'eau déminéralisée à 90°C, le calcul donne \(l_C\) = 2,4 mm, du même ordre de grandeur que 1,7 mm estimé précédemment.
Nous concluons sur cette partie en disant que la forme géométrique de la goutte a une conséquence bien visible sur les échanges énergétiques entre la plaque et la goutte.
Les expériences montrent que le débit de vapeur formée devient plus faible pour les gouttes sphériques, ce qui peut s'expliquer au regard de la forme de la surface de la goutte qui fait face à la plaque : une goutte aplatie présente une plus grande surface à la plaque qu'une goutte sphérique.
Cela nous a alors donné l'idée de voir si l'on pouvait trouver la dépendance entre une surface de la goutte en regard de la plaque, et la masse de vapeur perdue par unité de temps. Autrement dit, peut-on trouver une relation entre une surface caractéristique de la goutte et le débit massique ?
2.2 Surface caractéristique de la goutte et débit de vapeur
Pour cela, nous avons repris les résultats expérimentaux issus de la modélisation 3D précédente, et nous avons tracé l'évolution du volume d'une goutte de 200 μL au cours du temps, figure 16.
Figure 16. Évolution du volume de la goutte en fonction du temps Source : Clara Carlin, Gabriel Soleil, Naomie Viaud et Alexandre Dauger. |
Avant d'aller plus loin, prenons le temps de préciser les caractéristiques géométriques de la goutte. On appellera Rmax le rayon du disque de diamètre dmax, Rb, le rayon de la surface au bas de la goutte, et Smax et Sb les surfaces des disques de rayons respectifs Rmax et Rb, figure 17.
Figure 17. Quelques caractéristiques géométriques de la goutte Source : Clara Carlin, Gabriel Soleil, Naomie Viaud et Alexandre Dauger. |
Grâce à l'analyse du volume de la goutte réalisée toutes les 5 secondes, en multipliant le volume par la masse volumique, nous avons modélisé l'évolution de la masse m de la goutte au cours du temps, figure 18.
Figure 18. Modélisation de l'évolution de la masse de la goutte au cours du temps Source : Clara Carlin, Gabriel Soleil, Naomie Viaud et Alexandre Dauger. |
Nous avons pu dériver la masse m par rapport au temps, ce qui conduit au débit massique Dm de la goutte d'eau. Il ne nous restait plus qu'à tracer l'évolution du débit massique Dm en fonction de Smax, figure 19.
Figure 19. Modélisation de l’évolution du débit massique en fonction de la surface maximale Smax de la goutte Source : Clara Carlin, Gabriel Soleil, Naomie Viaud et Alexandre Dauger. |
Les points ont été modélisés par une fonction puissance, mais on s'aperçoit que la modélisation n'est pas correcte pour les faibles surfaces, c'est-à-dire pour les petites gouttes. Monsieur Florian Moreau, nous a proposé la lecture d'une publication dans laquelle un travail sur le débit massique avait été réalisé. L'évolution du débit massique y était tracée en fonction du rayon de la goutte. Nous avons alors fait de même, en fonction de Rmax et de Rb, figures 20 et 21.
Source : Clara Carlin, Gabriel Soleil, Naomie Viaud et Alexandre Dauger. |
Figure 21. Modélisation du débit massique en fonction du rayon Rb pour des grosses gouttes (non sphériques) Source : Clara Carlin, Gabriel Soleil, Naomie Viaud et Alexandre Dauger. |
On s'aperçoit alors que le débit massique de vapeur formée est proportionnel à Rmax, ou encore à Rb, sauf pour les faibles rayons.
En revenant sur le graphique du débit massique en fonction de Smax (figure 19), il apparaît très clairement que la modélisation par la fonction puissance n'est plus bonne pour les gouttes de surface Smax = 10 mm2. Or, cette valeur de surface correspond à la surface d'un disque de rayon 1,7 mm. C'est-à-dire qu'il s'agit justement de la valeur du rayon au-delà duquel la goutte déposée n'est plus sphérique.
Ces résultats expérimentaux et l'analyse que nous en avons faite confirment que l'évaporation de la goutte se fait selon deux régimes, selon son rayon et donc sa forme. En réalisant ces mesures, nous étions loin de nous douter que cela nous aiderait à comprendre et quantifier l'effet Leidenfrost.
3. Interactions entre les gouttes
3.1 Observations
Comme nous le soulignions dans la première partie, nous avons remarqué que lorsque l'on dépose une goutte d'éthanol et une goutte d'eau, ou bien une goutte d'acétone et une goutte d'eau sur la plaque, ces deux gouttes lévitent, conformément à l'effet Leidenfrost. Mais lorsqu'elles se trouvent en contact l'une de l'autre, elles préfèrent se repousser plutôt que coalescer. Ceci a éveillé particulièrement notre curiosité, car nous avons fait par ailleurs des expériences qui montraient une grande miscibilité entre l'eau et l'acétone, ou encore entre l'eau et l'éthanol. Et ce qui paraît encore plus étonnant, c'est qu'au bout d'un certain temps, elles finissent par coalescer, figure 22. Comment expliquer alors ces observations ?
Figure 22. Goutte d'eau et goutte d'éthanol puis goutte d'eau et goutte d'acétone Source : Clara Carlin, Gabriel Soleil, Naomie Viaud et Alexandre Dauger. |
3.2 Quelques hypothèses
Quels paramètres peuvent intervenir dans le processus étudié ? La densité ? La miscibilité ? Pour y voir plus clair, nous avons dressé un tableau qui récapitule les propriétés des différents liquides utilisés jusqu'à présent, tableau 1.
Tableau 1. Quelques caractéristiques de l'eau, de l'éthanol et de l'acétone
| Eau | Ethanol | Acétone |
Température d'ébullition | 100°C | 79°C | 56°C |
Température pour visualiser l'effet Leidenfrost | 200°C | 98°C | 89°C |
Masse volumique | 1 000 kg/m3 | 789 kg/m3 | 784 kg/m3 |
Tension superficielle | 73 mN/m | 22 mN/m | 23 mN/m |
Miscibilité | miscible dans l'éthanol et dans l'acétone | miscible dans l'eau et dans l'acétone | miscible dans l'éthanol et dans l'eau |
Polarité | polaire | polaire | polaire |
Ces caractéristiques montrent qu'il ne peut pas s'agir d'une question de miscibilité, ni de polarité. Il y a bien des différences de masses volumiques, mais nous ne voyons pas comment ces différences pourraient expliquer les observations. Alors nous nous sommes naturellement tournés vers la tension superficielle. En effet, la tension superficielle intervient dans la forme de l'interface entre deux fluides. Et on sait, en particulier, qu'un liquide tend à minimiser la surface de son interface avec l'air, pour des raisons de stabilité. Lorsque les liquides sont en contact, ils préfèrent alors coalescer dans le but de minimiser la surface en question. Alors est-ce que la tension superficielle peut expliquer le triple effet Leidenfrost ?
Et bien non… Car justement, dans un premier temps, cette coalescence ne se produit pas. Et lorsqu'on dépose une goutte d'eau et une goutte d'éthanol, ou encore une goutte d'eau et une goutte d'acétone sur la plaque froide, elles coalescent, au moins au niveau de leur zone de contact. Donc la tension superficielle n'explique pas l'effet observé, figure 23.
Source : Clara Carlin, Gabriel Soleil, Naomie Viaud et Alexandre Dauger. |
Que reste-t-il dans le tableau des caractéristiques ? La température d'ébullition. En effet, les températures d'ébullition de l'eau de l'éthanol et de l'acétone sont bien différentes. Lorsque la goutte d'eau est en lévitation sur la plaque, elle est à une température d'environ 90°C, alors que l'on a mesuré la température de la goutte d'acétone à environ 50°C.
Ainsi, nous pouvons très bien imaginer que lorsque la goutte d'acétone s'approche de la goutte d'eau, tout se passe comme si elle se rapprochait d'une autre surface chaude, mais cette fois-ci sur le côté, ce qui va provoquer de l'évaporation de la goutte d'acétone, mais sur le côté. Cela créé alors un film de vapeur supplémentaire qui va maintenir à distance la goutte d'acétone par rapport à la goutte d'eau. Et c'est pour cela qu'on peut appeler cet effet le triple effet Leidenfrost : chaque goutte se vaporise par le dessous, et la goutte d'eau crée une vaporisation de la goutte d'acétone sur le côté !
Il est clairement difficile de vérifier expérimentalement cette explication. On peut toutefois remarquer dans la vidéo figure 22, dans laquelle on a coloré la goutte d'eau en rouge, lorsque les gouttes se "cognent", la goutte d'acétone ne se colore pas du tout. Il n'y a pas d'échange entre la goutte d'eau et celle d'acétone. Et cela montre, en effet, que les deux gouttes n'entrent pas en contact, ce qui peut prouver l'existence d'un film de vapeur entre les deux gouttes.
Cela peut paraître surprenant qu'il y ait de façon quasi instantanée un film de vapeur qui se formerait lorsque la goutte d'acétone ou d'éthanol se rapproche de la goutte d'eau. Face à ce doute, nous avons eu l'idée de mesurer le temps nécessaire à la formation de ce film de vapeur. Pour cela, nous avons exploité le son produit lorsqu'on dépose une goutte sur la plaque chaude. Lorsqu'on fait cela, on entend un son très bref.
Comme ce bruit provient du contact entre la goutte et la plaque chauffante, nous avons pu évaluer le temps nécessaire pour que la goutte entre en lévitation en enregistrant le son et en analysant la bande son avec le logiciel Audacity.
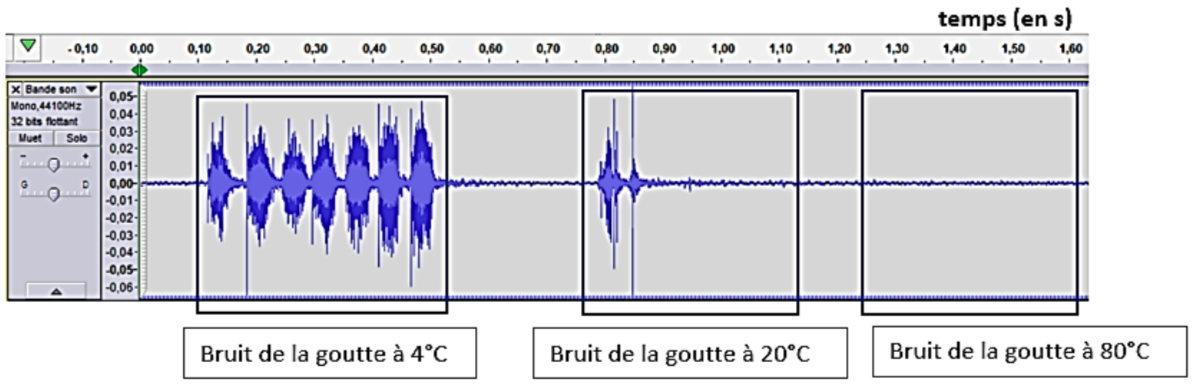
Nous avons réalisé des mesures avec des gouttes d'eau de températures différentes : une goutte d'eau à 4°C, une goutte d'eau à température ambiante, et une goutte d'eau à 80°C. L'étude du son a été réalisée avec le logiciel Audacity, figure 24.
Figure 24. Enregistrement des sons produits lors des dépôts d'une goutte froide, tiède, et chaude sur la plaque Source : Clara Carlin, Gabriel Soleil, Naomie Viaud et Alexandre Dauger. |
Nous observons que pour la goutte à 80°C, la goutte est immédiatement en lévitation, sans passer par un bref contact avec la plaque. Ce n'est pas le cas de la goutte à 20°C, qui entre en contact durant environ un dixième de seconde avant de léviter. Le cas de la goutte à 4°C est plus étrange, car outre le fait qu'il lui faille environ 4 dixièmes de seconde pour entrer en lévitation, la bande sonore témoigne d'un rebondissement de la goutte avant de léviter, selon une fréquence d'environ 15 Hz. Peut-être qu'un fort gradient de température à l'intérieur de la goutte provoque de forts mouvements de convection qui déforment la goutte, et qui seraient alors à l'origine de ces rebonds.
L'expérience montre, en tout cas, que pour les liquides à températures ambiantes, le film de vapeur se forme effectivement de façon instantanée, car la goutte d'acétone et d'eau sont déjà à la limite de l'ébullition lorsqu'elles se rencontrent.
Mais cela n'explique pas toutes les observations.
3.3 Pourquoi les gouttes finissent-elles par coalescer ?
Grâce aux expériences précédemment menées, nous suggèrons deux facteurs qui interviennent pour expliquer cela : la sphéricité des gouttes (donc pour des volumes inférieurs à 20 μL) et le débit massique de vapeur (plus faible pour des volumes de gouttes inférieurs à 20 μL).
Schématiquement, en tenant compte de ces deux facteurs, non seulement dans la situation de droite, le débit de vapeur d'acétone est moins élevé du fait de la forme sphérique de la goutte, mais en plus, le fait que la goutte a un petit rayon conduit la vapeur à s'échapper plus facilement sur le côté. De ces deux facteurs résulte le fait que le film de vapeur n'est plus suffisamment épais pour empêcher la coalescence des deux gouttes, figure 25.
Source : Clara Carlin, Gabriel Soleil, Naomie Viaud et Alexandre Dauger. |
Conclusion
Nous nous sommes intéressés à un phénomène avec une approche expérimentale, dans un premier temps pour mieux connaître l'effet Leidenfrost. Finalement, nous ne nous doutions pas que toute cette étude allait nous permettre de trouver une explication pour interpréter l'interaction entre les gouttes. C'est un projet qui nous a vraiment plu, d'une part pour son aspect visuel, mais aussi car il a soulevé de nombreuses questions auxquelles nous nous sommes amusés à répondre.
Pour citer cet article :
Observations de l'effet Leidenfrost, mai 2024. CultureSciences Physique - ISSN 2554-876X, https://culturesciencesphysique.ens-lyon.fr/ressource/Leidenfrost-Olympiades.xml