Activer le mode zen
Ressource au format PDF
Classification
Le tennis, c'est de la balle !
01/09/2020
Travail réalisé dans le cadre des XXVIIe Olympiades de Physique sous la tutelle de Marc Strubel, professeur de Physique-Chimie.
Résumé
À la fin de notre année de Première, nous avons décidé de poursuivre le travail commencé en TPE pour participer aux Olympiades de physique. Notre sujet portait sur le tennis et plus particulièrement le rebond de la balle. Il nous restait beaucoup à découvrir !
Nous avons constaté que le rebond d’une balle, sur une raquette ou sur le sol, dissipe plus ou moins d’énergie. Ainsi, nous avons d’abord cherché à déterminer quels paramètres influençaient ce rebond, en particulier la tension du cordage et la nature des cordes.
Nous avons ensuite étudié l’élasticité de la balle, pour comprendre que la balle ne se comporte pas comme un ressort mais montre de l’hystérésis, source de dissipation. Nous avons mesuré cette énergie dissipée de manière statique et dynamique. Nous avons filmé des chocs à haute vitesse pour estimer la force et la déformation de la balle, puis nous avons essayé de mesurer l’échauffement de la balle due au choc pour faire un bilan d’énergie. Enfin nous nous sommes interrogés sur l’utilité du feutre qui recouvre la balle, en découvrant qu’il absorbait beaucoup d’énergie au rebond.
Table des matières
1. Premiers rebonds : les balles
Une balle de tennis est une sphère en caoutchouc, remplie d'air et recouverte de feutre jaune ou blanc, figure 1. Il existe des balles sans pression et des balles pressurisées. Dans cette étude nous avons travaillé avec des balles non pressurisées. L'élasticité de la balle est essentiellement due au caoutchouc qui la compose et non à l'air à l'intérieur.
Figure 1. Balle de tennis coupée en deux |
Les principales caractéristiques des balles sont : leur masse, leur taille, le polymère et le revêtement qui les composent. D'après la reglementation de la férédration internationale de tennis (FIT) [1], une balle de tennis homologuée doit avoir un diamètre compris entre 6,350 cm et 6,668 cm, et sa masse doit varier entre 56,7 g et 58,5 g.
On teste le rebond d'une balle en la laissant tomber d'une hauteur de 254 cm (100 pouces) sur du béton ; un rebond entre 134,62 cm et 147,32 cm (53 et 58 pouces) est acceptable s'il a lieu au niveau de la mer, à 20°C, avec une humidité relative de 60% ; les balles utilisées à haute altitude ont différentes caractéristiques si elles sont testées au niveau de la mer.
Pour toutes nos expériences, nous allons utiliser des balles Head Tour neuves et des balles de marque Leclerc.
Notre première expérience a eu pour but de vérifier la hauteur de rebond indiquée dans les règles de la fédération internationale de tennis qui doit être comprise entre 134,62 cm et 147,32 cm. Nous avons laissé tomber, d’une hauteur de 254 cm, la balle de marque Head et la balle de la marque Leclerc, puis nous avons mesuré la hauteur de rebond. Les résultats sont présentés sur le tableau 1.
Tableau 1. Mesures de hauteur de rebond des balles
Numéro de lancer | 1 | 2 | 3 | 4 | 5 | 6 | hauteur moyenne de rebond (cm) |
Hauteur de rebond de la balle Head | 129 | 130 | 128 | 129 | 130 | 129 | 129 ± 1 |
Hauteur de rebond de la balle Leclerc | 86 | 85 | 84 | 86 | 89 | 88 | 86 ± 2 |
La valeur moyenne de rebond trouvée pour la balle Head est de 129 ± 1 cm ; elle est donc presque comprise dans l’intervalle de valeurs autorisées.
Pour cette balle, la perte d’énergie est :
ΔE = m g Δz = 58.10-3 × 9,81 ×(2,54 - 1,29) = 711 mJ
En notant hi la hauteur de lâché et hf la hauteur atteinte au rebond, on a :
hf / hi = 1,29/2,54 = 0,51
Pour la balle Leclerc, la perte d’énergie est plus grande :
ΔE = 956 mJ
Et hf / hi = 0,86/2,54 = 0,34
2. Rebonds sur une raquette
2.1 Les raquettes
Une raquette adulte cordée pèse de 270 g à 370 g. La longueur maximale d'une raquette est de 73,66 cm (29 pouces) et la longueur standard des raquettes adultes est de 68,5 cm. Le cordage peut être divers, mais il existe deux grandes familles : les naturels en boyau, et les synthétiques qui peuvent être monofilament (en polyester, kevlar, nylon, aramide, polyéthylène), multifilaments, guipés ou polyvalents, ils sont constitués d’une âme centrale de type monofilament (polyester ou nylon) autour de laquelle sont torsadés les filaments ; on applique par la suite une ou plusieurs gaines siliconées, ou enfin hybrides, par exemple boyau naturel sur les travers et monofilaments sur les montants, figure 2.
Figure 2. Structures des cordages synthétiques |
La jauge, souvent exprimée en millimètre ou en centième de millimètre, correspond au diamètre du cordage ; elle est généralement comprise entre 1,22 mm (jauge fine) et 1,28 mm (jauge épaisse).
La tension du cordage correspond à la force appliquée à chaque corde pour la tendre. Sa valeur se situe en général entre 20 kg et 30 kg soit entre 196 N et 294 N.
2.2 Influence de l’énergie initiale
Après avoir étudié le rebond sur le sol, nous avons étudié le rebond sur une raquette. Pour cela nous avons construit un dispositif avec la raquette fixe, et la balle lâchée d’une hauteur hi variable sans vitesse initiale, grâce à une trappe (figure 3) ; pour chaque valeur de lâché hi nous mesurons la hauteur de rebond hf.
Pour des raisons pratiques, nous avons choisi de fixer rigidement le tamis. Dans les conditions d'utilisation habituelles, c'est le manche qui est fixe, le résultat doit ici être un peu différent. Nous négligeons ainsi les vibrations entre le manche et le tamis. Dans ce montage nous avons fait de notre mieux pour limiter les vibrations résiduelles dues au choc de la balle sur le tamis.
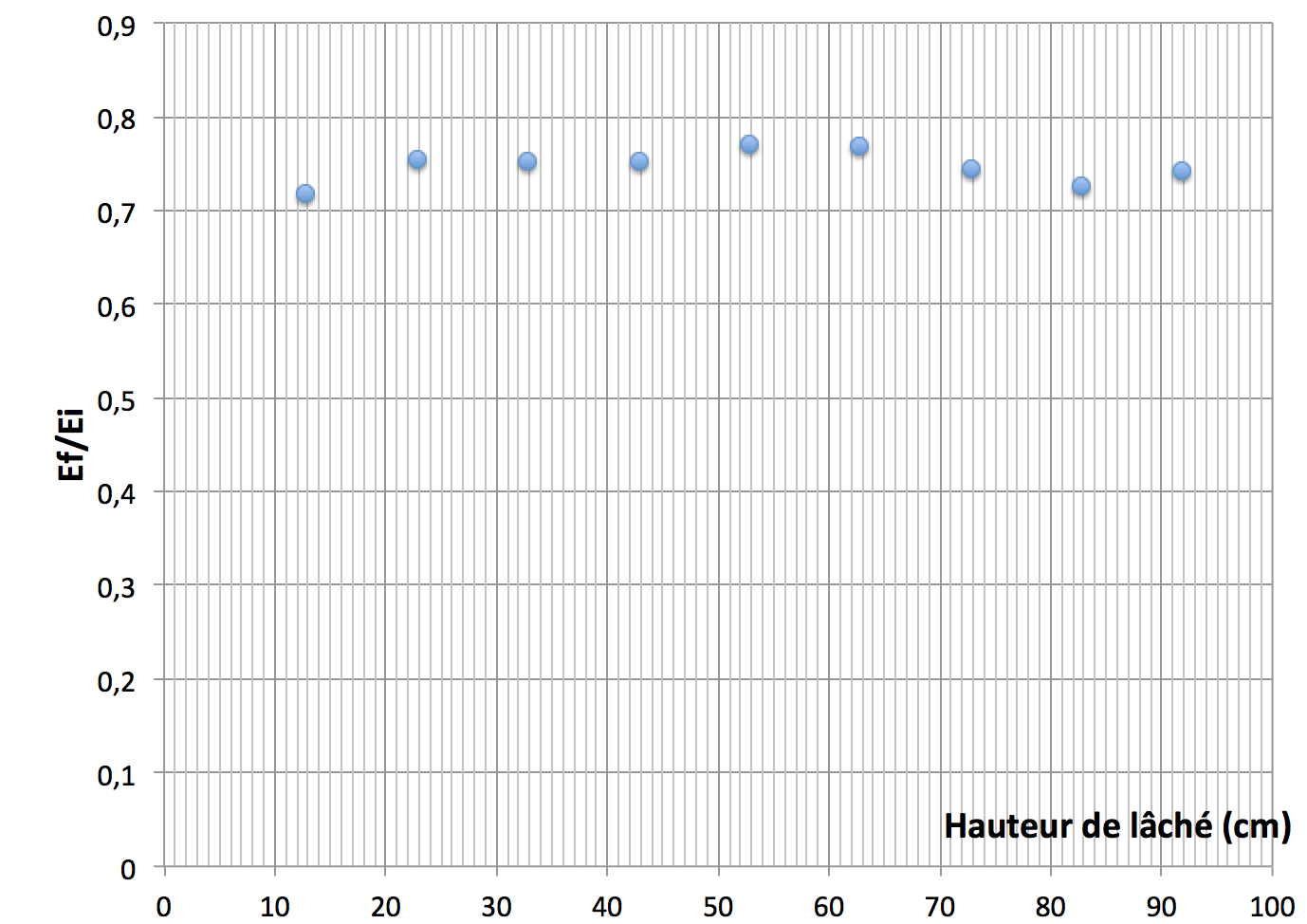
L’énergie initiale de la balle correspond à son énergie potentielle initiale : Ei = m × g × hi et son énergie potentielle finale : Ef = m × g × hf. Les résultats sont présentés figure 4 et 5. L’incertitude sur les hauteurs est évaluée à 2 mm.
On constate que l’énergie perdue par la balle représente toujours environ un quart (26%) de l’énergie initiale, mais si l'on compare au cas d’une chute sur le béton, on perd ici beaucoup moins d’énergie.
Mais où est perdue cette énergie ? Dans la raquette ou dans la balle ?
2.3 Influence de la tension du cordage
Nous avons souhaité savoir si la tension du cordage avait une influence sur le rebond. Pour pouvoir faire varier la tension, nous avons élaboré une raquette expérimentale composée d’un cadre en bois ainsi que de clefs de guitare qui permettent de tendre plus ou moins le cordage, figure 6. Ce cordage est monté à la place de la raquette sur le dispositif de mesure, figure 3.
Cette étude est réalisée de manière qualitative car pour plus de simplicité : la distance entre deux cordes est plus grande que sur une raquette et le tressage des cordes est aussi beaucoup plus lâche.
Grâce à ce montage nous avons pu faire varier le cordage (monofilament et multifilament) ainsi que la tension du cordage. La tension du cordage est mesurée à l’aide d’un haut-parleur : la tension, en Newton, est liée à la fréquence du fondamental de la corde en Hertz par la relation :
Avec la célérité de l'onde (m/s) : ; la tension de la corde (N) ; la masse linéique de la corde (kg/m) et la longueur de la corde = 20 cm.
Nous avons testé les rebonds pour un cordage monofilament ( = 1,7 g/m) et un cordage multifilament ( = 1,6 g/m).
Voici notre protocole expérimental : pour une tension de 10 kg (donc de 98 N) en monofilament, nous avons :
Pour régler la tension de 10 kg sur la corde monofilament, nous écoutons à l'aide d'un GBF branché à un haut-parleur le son produit par le signal de 600 Hertz et accordons la corde, comme sur une guitare.
A posteriori, les incertitudes sont difficiles à estimer sur la précision de ce protocole. On aurait pu utiliser un accordeur (objet ou application smartphone) pour un réglage plus fin.
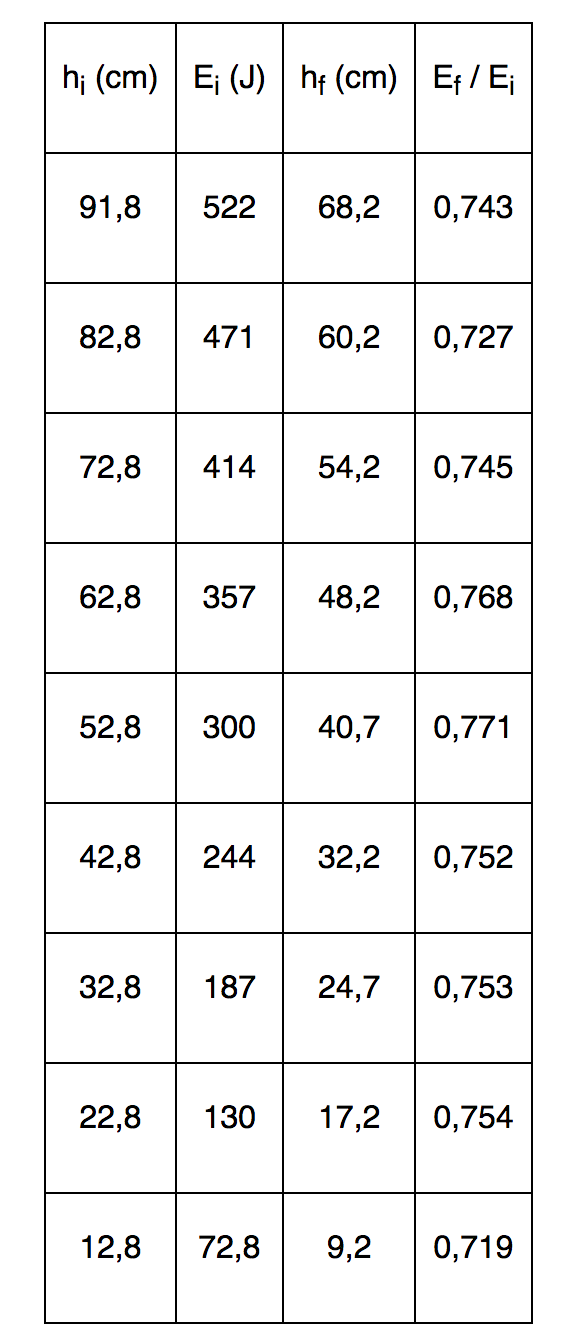
Voici le tableau que nous avons pu établir pour une hauteur de lâché hi = 92,5 cm , tableau 2.
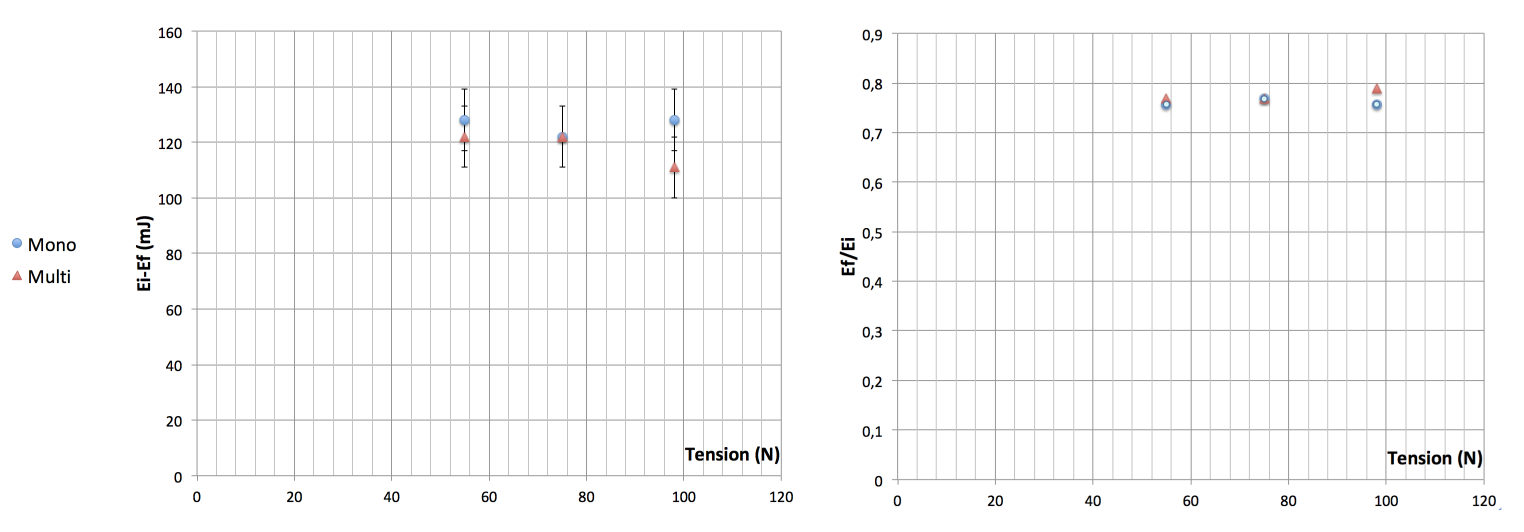
Tableau 2. Hauteurs de rebond et énergies potentielles des balles avant et après rebond en fonction de la tension et de la composition du cordage
f (Hz) | T (N) | Ei (mJ) | hf (cm) | Ef (mJ) | Ei - Ef (mJ) | Ef / Ei | |
Mono
| 600 | 98 | 526 | 70 ± 1 | 398 ± 6 | 128 ± 6 | 0,757 |
525 | 75 | 526 | 71 ± 2 | 404 ± 12 | 122 ± 12 | 0,768 | |
450 | 55 | 526 | 70 ± 2 | 398 ± 12 | 1288 ± 12 | 0,757 | |
Multi
| 618 | 98 | 526 | 73 ± 2 | 415 ± 12 | 111 ± 12 | 0,789 |
561 | 75 | 526 | 71 ± 2 | 404 ± 12 | 122 ± 12 | 0,768 | |
464 | 55 | 526 | 71 ± 2 | 404 ± 12 | 122 ± 12 | 0,768 |
Encore une fois, nous précisons qu'ici on est loin des conditions de jeu du tennis (vitesses des balles, tension du cordage, espace entre les cordes, tressage du tamis, raquette tenue fixe par le manche...)
Les mesures ne sont pas significatives, les incertitudes de mesure sont trop élevées ; on peut conclure que la différence de comportement des deux types de cordage n’est pas flagrante à faible vitesse.
Conclusion : quel que soit le type de rebond, une énergie entre 100 mJ et 200 mJ est perdue par la balle ; il est peu probable que cette énergie ait été transférée au cordage, qui est beaucoup plus rigide que la balle. Où est alors passée cette énergie ?
3. Étude de la déformation de la balle
3.1 Étude statique
À titre d'illustration et bien que nous nous éloignions encore une fois des conditions de jeu du tennis, nous avons souhaité étudier la déformation statique d'une balle de tennis.
Pour comprendre où l’énergie est perdue, nous voulons étudier le rapport entre la force appliquée à la balle et sa déformation, figure 8.
Dans ce montage, la plaque de bois fine à droite de la balle nous sert à la compresser sur la partie plus épaisse de gauche. La plaque de droite est vissée sur une jauge de contrainte reliée à un amplificateur HX711 et une carte Arduino.
La partie de gauche, avec la “manivelle”, nous permet de comprimer la balle en comptant le nombre de tours (ou demi-tours) et la compression correspondante.
Pour établir cette correspondance tours-compression, nous avons mesuré que 50 filets de la vis correspondent à une distance de 4,0 ± 0,1 cm.
Pour 1 tour, on compresse la balle de Δx = 0,004 / 50 = 0,8 ± 0,002 mm
Étalonnage du capteur
La tension U renvoyée par la carte Arduino est reliée à la force exercée sur le capteur par la loi :
F = aU + b
Au démarrage, le logiciel tare, on a : b = 0
Dans la loi F = aU, a est le facteur de calibration. Pour étalonner le capteur, nous avons suspendu une masse définie (1 kg) au capteur et avec l’affichage en direct du programme, nous modifions le facteur de calibration pour afficher une force de 9,8 N.
On en déduit le facteur de calibration correspondant au capteur. Cette manipulation doit être effectuée pour chaque nouveau capteur (celui de 20 kg dans notre cas).
Mesures
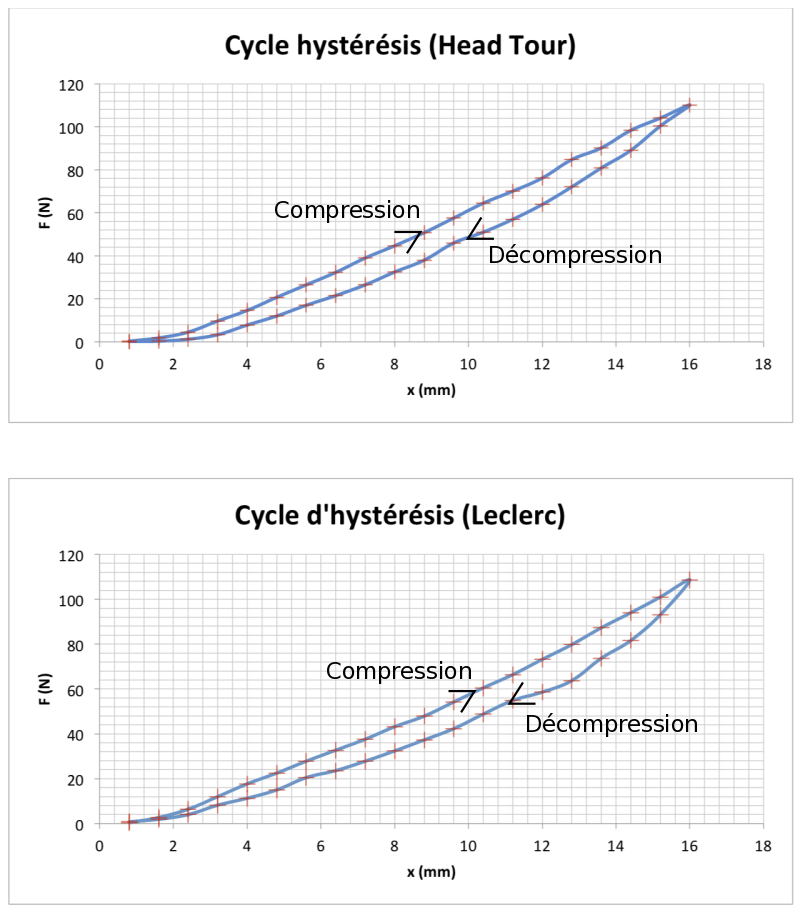
À l'aide du dispositif, nous avons progressivement compressé la balle en mesurant la compression x (en mm) et la force de compression F (en N). Cette expérience a été réalisée deux fois avec les deux balles : une balle Head et une balle Leclerc, figure 9.
La courbe obtenue montre un cycle d’hystérésis qui traduit une dissipation de l’énergie du système étudié (la balle). Dans le cas d'un ressort, le tracé serait linéaire. Le ressort restitue toute son énergie.
La balle, entre son état initial (avant déformation) et son état final (après déformation) n’a pas restitué toute son énergie, une partie s’est dissipée : elle correspond à l’aire du cycle tracé, ce que nous pouvons écrire :
Pour les deux cycles, la balle a été comprimée jusqu’à xmax = 16,0 mm.
Tableau 3. Comparaison des caractéristiques des deux types de balles
| Fmax (N) | Énergiemax (mJ) | Énergie dissipée : aire du cycle (mJ) | Énergiemax/Énergie dissipée |
Balle Head Tour | 110,0 | 1763 | 136 | 13,0 |
Balle Leclerc | 108,6 | 1740 | 134 | 13,0 |
On remarque que dans les deux cas l’énergie dissipée est de l’ordre de Fmax.xmax/13.
Conclusion : on ne fait pas la différence entre l’énergie dissipée entre les deux balles avec une compression statique ; le comportement du polymère dépend de la vitesse avec laquelle il est sollicité ; il faut faire ces mesures en dynamique.
3.2 Étude dynamique
À l'aide de notre montage expérimental à trappe/tiroir (figure 3), nous avons voulu étudier la dissipation d'énergie d'énergie dans la balle à faible vitesse dans des conditions reproductibles avec possibilité de faire varier la hauteur.
Avec le capteur à jauges de contraintes relié à la carte Arduino, nos résultats étaient imprécis, le capteur continuait d’osciller après le choc avec la balle, ce qui nous empêchait d'interpréter proprement les résultats de l’expérience.
Nous avons essayé plusieurs autres capteurs sans grand succès, de plus il était impossible de mesurer la compression de la balle de manière instantanée en dynamique, aussi nous avons décidé de passer en vitesse « réelle » dans un club de tennis.
4. Étude énergétique d'une balle avec vitesse initiale
Nous allons à présent nous intéresser à l’étude de la balle ayant une vitesse plus élevée que dans le travail précédent, et mesurer l'énergie de la balle avant et après rebond sur la raquette.
Pour cela nous avons utilisé un lanceur de balle de tennis, le Spin Shot Player, qui simule des frappes à plat c’est-à-dire sans effet. Nous avons accroché une raquette par le manche et le haut du cadre sur un support (une chaise d'arbitre) à une distance fixe de la machine.
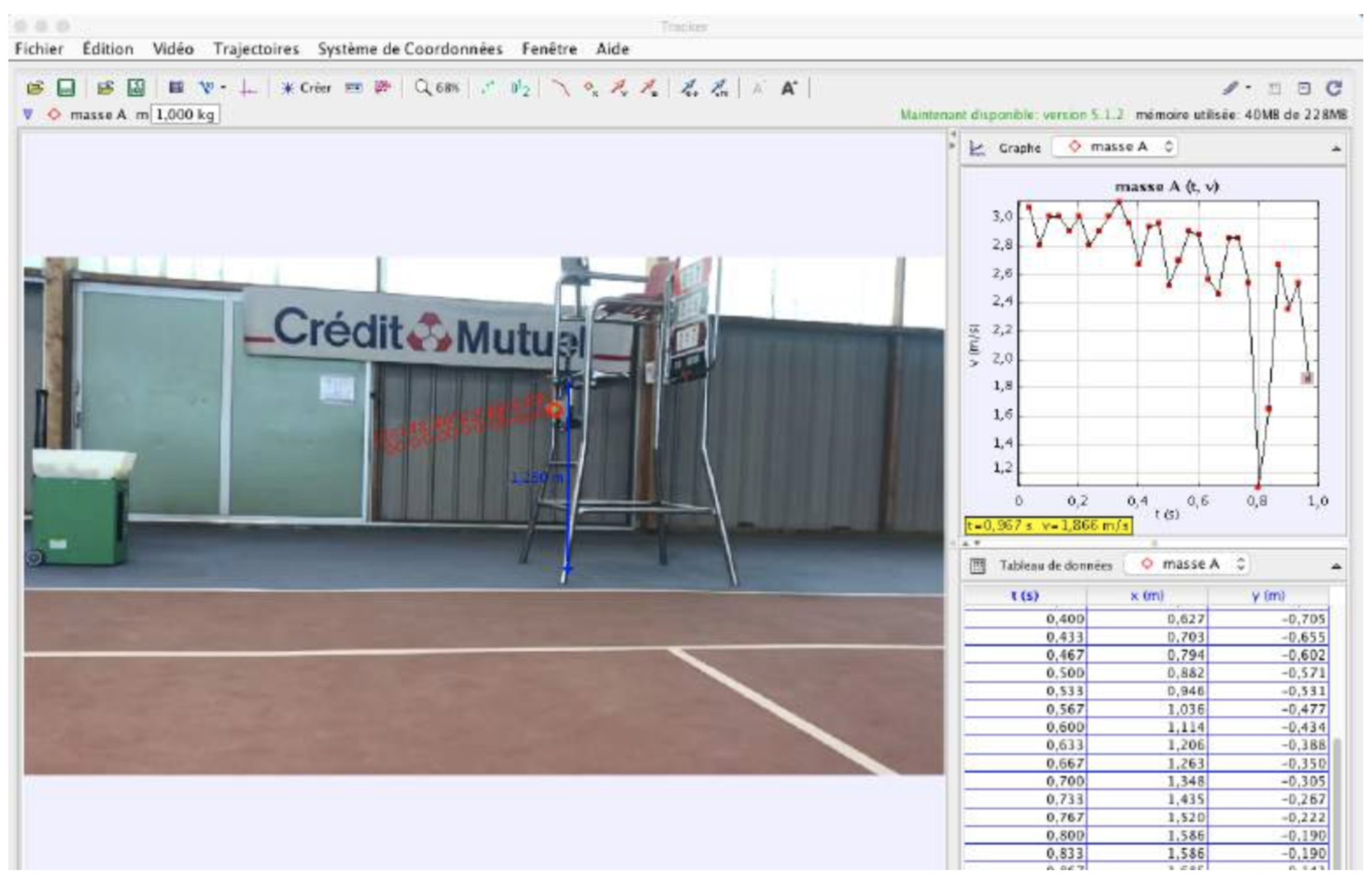
Pour étudier les vitesses avant et après rebond, nous avons réalisé des vidéos avec un smartphone filmant à 240 images par seconde et utilisé le logiciel de pointage Tracker afin d’exploiter nos images, figure 10.
Figure 10. Analyse d'une vidéo avec le logiciel Tracker |
Sur la figure 10, on peut voir que le logiciel Tracker calcule par défaut avec une cadence de 30 images par seconde, donc il faut multiplier les valeurs de vitesse obtenues par 240/30 = 8.
Nos résultats sur la meilleure vidéo réalisée sont :
Numéro du film | Vi (m/s) | Vf (m/s) | Eci (J) | Ecf (J) | ΔEc |
3764 | 20 ± 0,8 | 17 ± 0,2 | 11,6 ± 1,0 | 8,6 ± 1,2 | 3,0 ± 1,6 |
Malgré les très grosses incertitudes (dues au pointage du centre de la balle), on constate que la perte d’énergie est cette fois de :
ΔEc = 3,0 ± 1,6 J
Remarque : la perte d’énergie représente 3/11,6 = 0,26 soit 26% de l’énergie incidente, comme dans l'expérience du lâché de balle par la trappe (figure 3).
5. Échauffement de la balle
5.1 Calorimétrie
L’énergie dissipée doit se retrouver sous forme d’énergie thermique dans la balle. Afin de mesurer le transfert d’énergie thermique dans la balle, il nous est nécessaire de connaître sa capacité calorifique.
Grâce à une expérience de calorimétrie, nous avons déterminé la capacité calorifique d’une balle de tennis (type Leclerc). Au préalable, nous avons découpé la balle de tennis en petits morceaux et l’avons placé dans une étuve à une température constante Ti = 108°C. Le couvercle du calorimètre est percé de deux trous dans lesquels nous avons placé un thermomètre et un agitateur. Après avoir déposé 200 mL (m0 = 200 g) d’eau à T0 = 22,5°C dans le calorimètre, on a introduit rapidement les morceaux de balle avant de fermer le couvercle. Nous avons préalablement démarré une acquisition sur Latis-pro pour récupérer en direct la température dans le calorimètre et étudier son évolution au cours du temps. Les mesures du thermomètre sont envoyées en direct à Latis-pro via l’interface. Nous avons attendu que la température se stabilise avant de terminer l’acquisition.
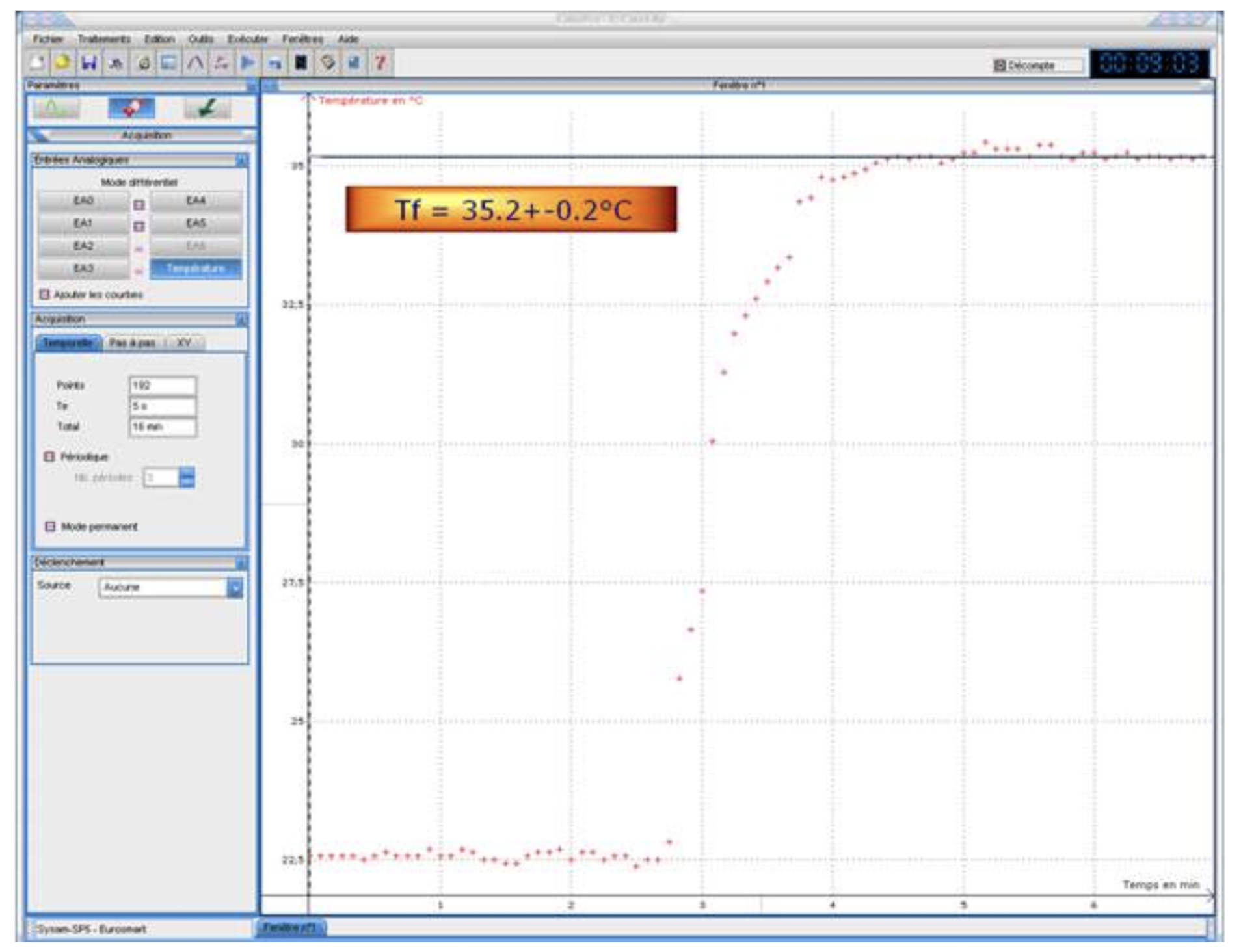
La figure 11 présente les résultats que nous avons obtenus.
La température finale est Tf = 35,2 ± 0,2°C. Ces résultats nous permettent de calculer la capacité calorique c de la balle de tennis étudiée :
1,66 J.g-1.K-1
Où μ = 46 g est la masse d'eau initiale d'eau dans le calorimètre, m0 = 200 g la masse initiale introduite d’eau, m = 111 g la masse des morceaux de balle, c0 = 4,18 J.g-1.K-1 la capacité calorifique de l’eau, Ti et Tf respectivement les températures mesurées en début et en fin d’expérience et T0 la température de l’eau placée dans la cuve au début.
Nous ne savons pas de quel polymère est fait la balle, mais le caoutchouc naturel a par exemple une capacité calorifique de c = 2,09 J.g-1.K-1, proche de notre mesure.
5.2 Mise en évidence du transfert d’énergie
Nous avons souhaité mettre en évidence l’énergie thermique dissipée dans la balle ; cette énergie étant faible, il nous fallait comprimer la balle de nombreuses fois, afin de mettre en évidence l’échauffement de la balle.
Nous avons construit un dispositif à partir d’une scie sauteuse, permettant de comprimer la balle Head Tour plusieurs fois par minute. Nous avons inséré un thermomètre dans la balle pour mesurer sa variation de température, figure 12.
Pour mesurer le nombre de compressions pendant la durée d’étude ∆t, il faut connaître le nombre de compressions par seconde, donc la fréquence f de la scie ; nous avons alors utilisé un stroboscope et nous avons mesuré f = 55 Hz.
Le nombre de compressions est donc N = f × ∆t.
La course de la tête : x = 1,8 ± 0,1 cm, correspond à la compression. En utilisant les résultats obtenus par la jauge de compression statique, on estime alors la force maximale à Fmax = 140 N. On peut donc minorer les pertes pour une compression par :
ΔE = F.x / 13 = 140×1,8.10-2/13 = 193 mJ
Avant compression, la température à l'intérieur de la balle est Ti = 20,3°C.
Nous avons réalisé plusieurs mesures de même durée ∆t = 45 secondes de frappe avec notre dispositif, la moyenne des températures finales obtenues est :
Tf = 32 ± 2°C.
L’énergie thermique gagnée à l'intérieur de la balle pour une compression vaut donc :
436 mJ
Conclusion : on retrouve encore une valeur plus grande que la valeur estimée en statique. Restons encore vigilant sur notre conclusion car nous venons de déterminer l'énergie thermique gagnée à l'intérieur de la balle. Il faudrait mesurer la température du caoutchouc et de la surface de la balle pour comparer avec les résultats obtenus par l'étude statique.
6. Utilité du feutre
Initialement, nous souhaitions refaire l’expérience de calorimétrie avec une balle « chauve », obtenue en enlevant le feutre. Et en manipulant cette balle, nous avons alors réalisé qu’elle rebondissait beaucoup mieux, ce qui montre qu’une partie de l’énergie est absorbée par le feutre.
6.1 Rebonds
Nous avons repris l’expérience figure 3 avec une balle « chauve ». Voici les résultats :
hi (cm) | Ei (mJ) | hf (cm) | Ef/Ei |
88,0 | 501 | 72,3 | 0,82 |
78,0 | 444 | 65,0 | 0,83 |
68,0 | 387 | 56,3 | 0,83 |
58,0 | 330 | 53,0 | 0,91 |
48,0 | 273 | 40,8 | 0,85 |
38,0 | 216 | 34,0 | 0,89 |
Conclusion : la valeur moyenne de Ef/Ei est de 0,86 : le feutre absorbe environ 0,86-0,75 = 0,11 soit 11% de l’énergie au rebond, seuls les 14% restants sont dissipés dans le polymère.
6.2 Mesures de trainée
Nous nous sommes alors demandés quelle était l’utilité du feutre ? Notre première hypothèse concernait le vol de la balle : le feutre permettrait-il de réduire la trainée aérodynamique ?
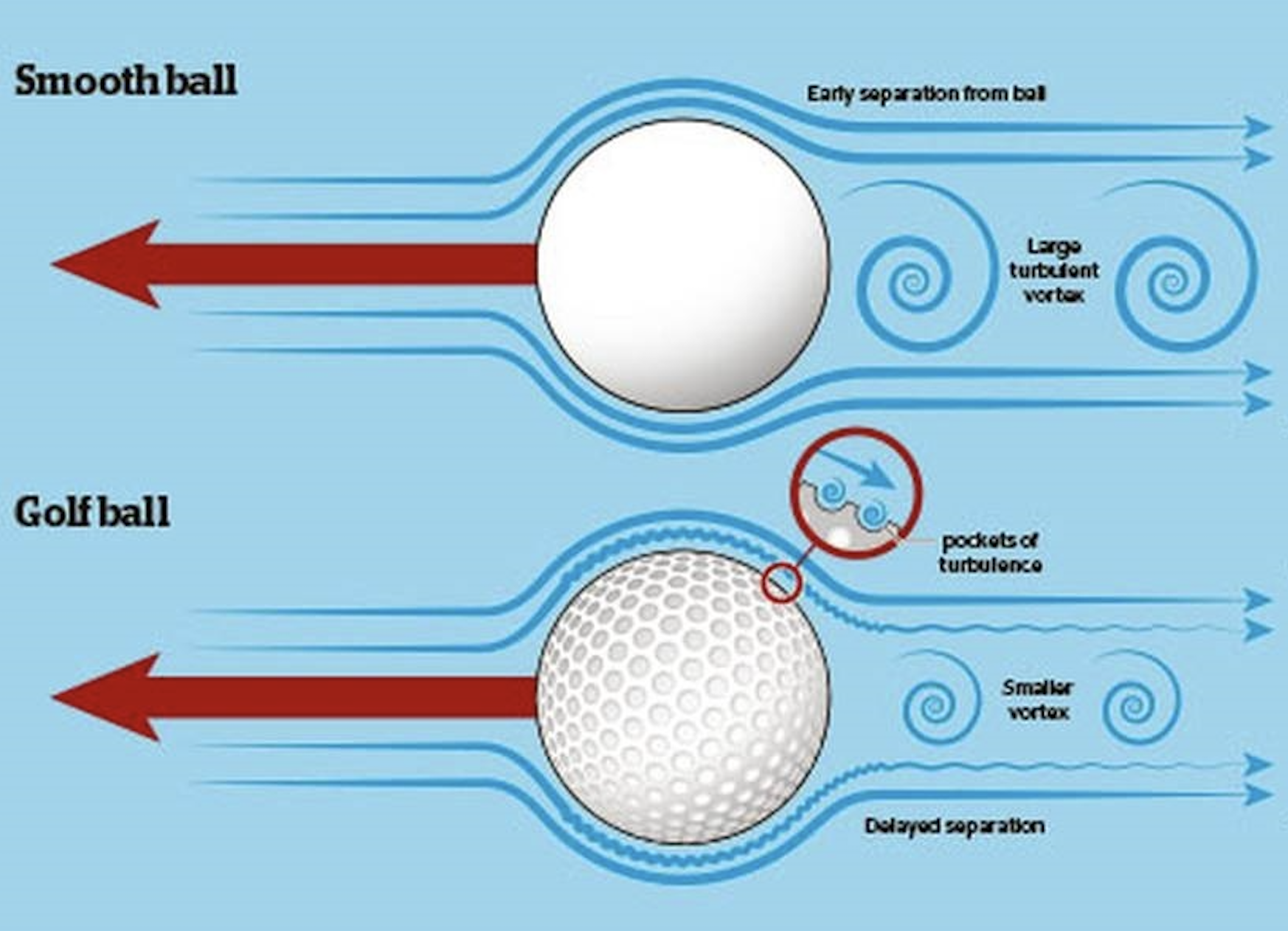
Dans la littérature, on apprend que les alvéoles présentes sur les balles de golf, ont pour fonction, à grande vitesse, de faciliter le décollement de la couche limite et donc de réduire la traînée de la balle. L'intérêt est d'améliorer l'aérodynamisme de la balle.
Nous avons alors réalisé des essais en soufflerie au labo de prépa du lycée et mesuré la trainée pour une balle « chauve » et la balle « avec feutre », figure 14.
La vitesse de l’air dans la soufflerie a été mesurée à l’aide d’un tube de Pitot. Nous souhaitions nous placer à une vitesse caractéristique pour des balles de tennis, soit v = 20 m.s-1, mais la soufflerie ne permet d’aller que jusqu’à la vitesse de 14,5 m.s-1.
À cette vitesse on mesure :
- Balle chauve : F = 0,28 ± 0,02 N
- Balle avec feutre : F = 0,44 ± 0,02 N
Conclusion : la trainée est donc supérieure pour la balle avec feutre, ce qui contredit notre hypothèse initiale.
7. Conclusions
Qu'avons-nous appris au cours de ce travail ?
Concernant la balle, on peut dire que son comportement au rebond dépend beaucoup de sa vitesse : à très faible vitesse, chaque choc dissipe environ 13% de l’énergie de la balle. À une vitesse de jeu classique pour le tennis, elle dissipe cette fois entre deux à quatre fois plus d'énergie.
Le feutre est responsable de presque un tiers de l’énergie dissipée ; mais est très important, d'après les joueurs, pour l'accroche de la balle dans la raquette et donc la possibilité de mettre des effets dans la balle.
Nous avons enfin appris, qu’une expérience simple, ça n’existe pas, du moins pas si on veut en tirer des conclusions ! Avons-nous pensé à tout ? N’y a-t-il pas un paramètre oublié ? Avons-nous tout bien noté ? Nous avons beaucoup progressé grâce à ce travail.
Remerciements
Merci à Arnaud BOIRON, agrégé préparateur au lycée SCHWEITZER, Olivier NUSSBAUM, professeur de tennis à Kingersheim et Valérie SEBIRE, du magasin Court Annexe de Brunstatt.
Références
- [1] Propriétés des balles de tennis.
- [2] Dynamic properties of tennis balls, Rod Cross, Sports Engeneering, 1999.
- [3] The bounce of a ball, Rod Cross, Rod Cross, American Journal of Physics n°67, mars 1999.
- [4]Règles du tennis.
- [5] Page personnelle de Rod Cross, un spécialiste de la physique du tennis.
- [6] The physics of tennis
- [7] What’s in a Tennis Ball Besides Rubber ?
Pour citer cet article :
Le tennis, c'est de la balle !, Caroline Amis, Danaé Makowka, Loïck Abgrall, septembre 2020. CultureSciences Physique - ISSN 2554-876X, https://culturesciencesphysique.ens-lyon.fr/ressource/tennis-olympiades.xml