Activer le mode zen
Ressource au format PDF
Classification
Comment réfrigérer une canette en moins de trois minutes
25/05/2021
Travail réalisé dans le cadre des XXVIIIe Olympiades de Physique sous la tutelle des professeurs Jean-Christophe Jouan et Yves Chriqui.
Résumé
La première partie de notre travail a consisté à nous documenter sur les différentes techniques de ≪ production ≫ du froid et faire quelques expériences qualitatives préliminaires pour tester les solutions envisageables. C’est à l’issue de cette première phase de recherche que nous nous sommes rendus compte que la ≪ production ≫ de froid en quantité et en temps limité n’était pas si facile à réaliser. Nous avons néanmoins trouvé une solution basée sur l’utilisation du congélateur de la cuisine. Nous avons ensuite cherché à optimiser le transfert thermique avec la canette de façon à descendre sous la barre des 3 minutes. Cette deuxième étape d’optimisation nous a permis d’atteindre l’objectif visé. À cette occasion, nous avons développé une solution originale et innovante pour augmenter les capacités de réfrigération du dispositif : l’absorbeur de chaleur. Dans un troisième et dernier temps nous nous sommes intéressés à la physique du transfert thermique mis en jeu dans l’expérience afin de valider le modèle théorique de la loi de Newton. Nous avons observé un écart à cette loi que nous interprétons et qui peut être mis à profit pour garder la canette fraîche plus longtemps.
Table des matières
Problématique
Par une chaude journée d'été l’envie vous prend de savourer une canette de soda bien fraîche. Vous ouvrez votre réfrigérateur et… déception, il n’y a plus de canette au frais. Qu’à cela ne tienne, vous prenez une canette à température ambiante et la placez dans votre congélateur en espérant la boire fraîche rapidement. Il vous faudra attendre 30 à 40 min avant de vous rafraîchir. L’idée suivante vous vient alors :
Peut-on rafraîchir une canette en moins de trois minutes ?
Tel est le point de départ du projet « Cool Canette » que nous avons développé en partenariat avec la société Air Liquide et l’équipe R&D de M. Nicolle. Le projet consiste à refroidir une canette de 33 cL depuis la température ambiante (20°C) à la température de 5°C en moins de trois minutes avec des moyens simples à disposition dans une cuisine. Tout le monde ne dispose pas en effet d’une réserve d’azote liquide (à −196°C) dans sa cuisine pour les besoins de réfrigération !
1. Comment produire du froid ?
Commençons par quelques chiffres pour préciser l’objectif visé.
Refroidir 33 cL d’eau de = 20°C à = 5°C nécessite d’extraire une quantité de chaleur :
Le transfert ayant lieu en trois minutes, cela correspond à une puissance thermique :
Voyons maintenant les différentes solutions de refroidissement compatibles avec ces données.
1.1 Les machines frigorifiques : le congélateur
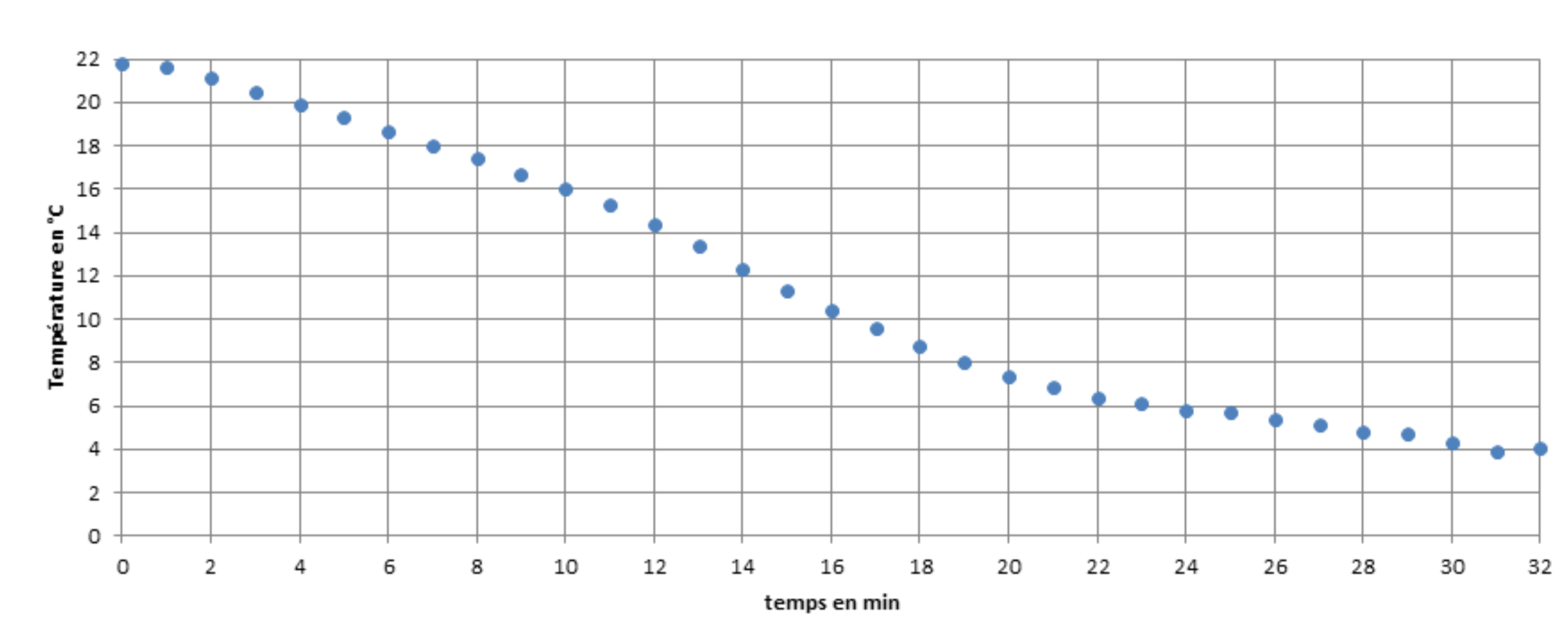
Le premier réflexe pour refroidir la canette est de la mettre au congélateur. Réalisons l’expérience suivante : la canette contenant 33 cL d'eau à température ambiante est placée au congélateur et relevons la température au centre de la canette toutes les minutes. Nous obtenons la courbe de refroidissement de la figure 1.
Nous découvrons que le temps de refroidissement pour atteindre 5°C est bien supérieur à 3 minutes et avoisine les 27 minutes, malgré la température intérieure du congélateur qui frôle les −30°C (c’est la température du congélateur du laboratoire ; la température intérieure d’un congélateur domestique est plus proche de −20°C). La puissance thermique moyenne de réfrigération est de :
Pour le calcul nous avons pris en compte la capacité thermique de la canette qui est équivalente à celle de 18 g d’eau.
1.2 Froid physique et changements d’état
Le deuxième réflexe, pour refroidir une boisson est d’y introduire des glaçons.
La fusion d’un kilogramme d’eau à 0°C nécessite un apport d’énergie thermique de 334 kJ, appelée chaleur latente de changement d’état et notée = 334 kJ kg-1. Cette énergie est prélevée au milieu ambiant qui se refroidit. Ainsi, on peut déterminer la masse de glace nécessaire au refroidissement de 33 cL d’eau de = 20°C à = 5°C :
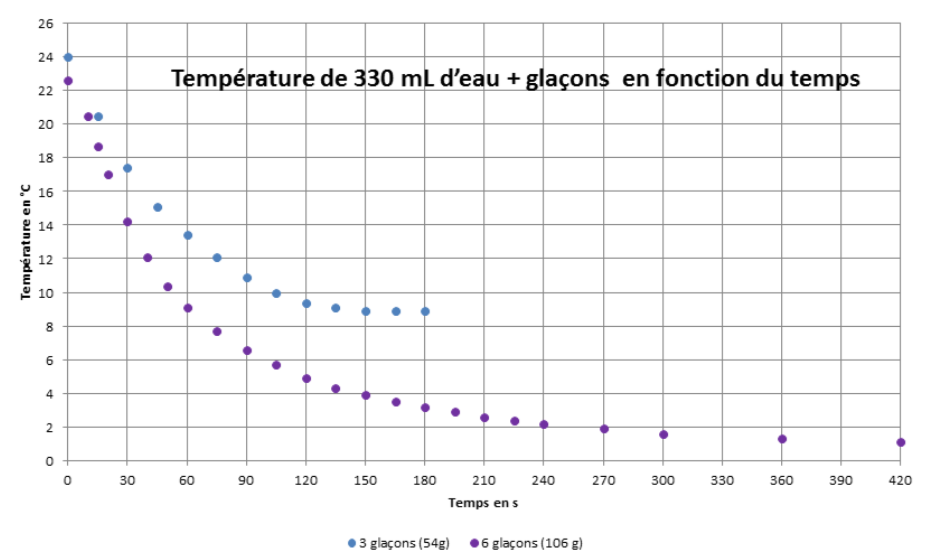
Réalisons alors l’expérience suivante : dans un bécher agité contenant 330 mL d’eau à température ambiante, introduisons une masse de glace voisine de la masse calculée précédemment et mesurons la température en fonction du temps.
Nous obtenons les courbes de la figure 2, dans le cas où on ajoute 54 g de glace (3 glaçons) en bleu et 106 g de glace en violet. La courbe correspondant aux trois glaçons atteint un pallier au bout de 150 s correspondant à la fusion complète des glaçons.
Nous voyons sur cette courbe l’efficacité de la fusion dans le processus de refroidissement. La puissance thermique moyenne de réfrigération pour atteindre 5°C dans le cas de la courbe avec les 6 glaçons est de 212 W ! La technique possède néanmoins un inconvénient : elle nécessite d’introduire une grande quantité de glace dans la boisson, donc d’eau ce qui risque d’en altérer le goût. Malgré son efficacité nous ne retenons pas cette solution.
La vaporisation de l’eau à 100°C sous la pression atmosphérique, est bien plus efficace d’un point de vue énergétique car elle nécessite un apport d’énergie thermique 10 fois plus grand que celui nécessaire à la fusion. En effet, la vaporisation d’un kg d’eau nécessite un apport de 2265 kJ ( lvap = 2 265 kJkg-1) Ainsi la masse d’eau nécessaire pour refroidir la canette serait seulement de :
Seulement, pour que la vaporisation se produise à température ambiante, il faudrait travailler sous pression réduite de 23 mbar.
Une autre solution, consisterait à utiliser un liquide qui se vaporise à la température ambiante à une pression supérieure à la pression atmosphérique. Le liquide maintenu sous pression, à la température ambiante, est détendu et se vaporise. C’est sur ce principe que reposent les bombes de froid utilisées par les sportifs qui permettent d’atteindre localement une température de −40°C comme nous avons pu le constater en pulvérisant le liquide sur l’extrémité d’un thermomètre. La difficulté avec ces techniques de vaporisation, comme nous avons pu le constater expérimentalement, est d’optimiser le transfert thermique avec la canette. En effet, la chaleur nécessaire à la vaporisation du liquide est prélevée en partie à la canette et en partie à l’air ambiant.
Terminons en citant le phénomène d’évaporation responsable de la sensation de froid que l’on ressent lorsque notre peau est mouillée (principe du brumisateur, ou du réfrigérateur pot en pot) ou suite à l’évaporation de gel hydroalcoolique sur la peau. L’évaporation est un phénomène lent mais qui peut être accéléré en présence d’un courant d’air. La lenteur du phénomène nous a conduit à mettre cette solution de côté après quelques tests non concluants.
À ce sujet on pourra consulter l'article « Zeer ou le Frigo du Désert »
Le « frigo du désert » ou Zeer, est un système de refroidissement sans électricité utilisé dans les pays chauds et secs et fondé sur l’évaporation d’eau.
1.3 Froid chimique et mélanges réfrigérants
L’ajout de sel de cuisine (chlorure de sodium NaCl(s)) à de la glace pilée permet d’obtenir une température négative. Théoriquement, l’ajout de 30 g de sel à 100 g de glace permet d’atteindre une température de −20°C [1].
Pour tester l’efficacité du refroidissement, nous avons fait les expériences qualitatives suivantes : une canette contenant 33 cL d’eau à température ambiante voisine de 20°C est plongée dans différents mélanges réfrigérants. Nous mesurons la température au centre de la canette ainsi que le temps nécessaire pour atteindre 5°C. La photo de la figure 3 montre le montage expérimental : nous travaillons dans un calorimètre de façon à limiter les échanges thermiques entre le mélange réfrigérant et l’air ambiant.
Les résultats sont résumés dans le tableau 1.
Tableau 1. Durée de refroidissement de la canette suivant le mélange réfrigérant
Type de mélange | Durée (min) |
eau/glace à 0°C | 20 |
eau/glace à 0°C et agitation du contenu de la canette | 15 |
sel/glace pilée à −12°C (température initiale du mélange) | 6 |
sel/glace pilée à −12°C (température initiale du mélange) et agitation du contenu de la canette | 5 |
Ces expériences qualitatives montrent que les mélanges réfrigérants constituent un meilleur thermostat que l’air du congélateur. La glace et l’eau sont de meilleurs conducteurs thermique que l’air. De plus leur capacité thermique plus élevée que celle de l’air limite leur échauffement par rapport à l’air pour un même transfert thermique.
Nous observons aussi que plus la température du mélange réfrigérant est basse, plus le refroidissement est rapide.
Ces expériences montrent également le rôle fondamental de l’agitation dans le processus de refroidissement.
Notons qu’il est possible d’atteindre des températures encore plus basses à l’aide d’autres mélanges réfrigérants [1]. Ainsi le mélange de 100 g de glace pilée (0°C) avec 143 g de chlorure de calcium hydraté CaCl2, 6H2O(s) doit permettre de descendre à −55°C. Une substance comme CaCl2 , 6H2O(s) n’étant pas d’usage courant, nous mettons provisoirement cette solution de refroidissement de côté. D’autant que le processus n’est pas réversible et ne permet pas de réutiliser le mélange une fois utilisé.
1.4 Détente de gaz
Un gaz quand il se détend se refroidit. C’est le principe utilisé par notre partenaire pour obtenir de l’air liquide (procédé Claude). C’est aussi la détente de gaz qui est mise à profit dans un congélateur pour refroidir le liquide réfrigérant avant que ce dernier ne se vaporise pour refroidir l’intérieur du congélateur.
Considérons de l’air détendu et refroidi à une température de −20°C. La capacité thermique volumique de l’air étant de CV = 0,8 JK-1L-1, nous pouvons évaluer le volume d’air nécessaire pour refroidir la canette, en supposant que l’air se réchauffe de = −22°C à = 0°C.
De l’ordre de 1 m3, le volume d’air est important et rend le système peu pratique à utiliser. Par ailleurs comme l’a montré l’expérience réalisée avec le congélateur, l’air est un mauvais conducteur thermique ce qui nous conduit à mettre cette solution de côté.
1.5 Autres effets thermiques
Effet Peltier
Quand une jonction entre deux métaux de natures différentes est parcourue par un courant, elle libère ou absorbe de la chaleur selon le sens du courant. Cet effet a été découvert en 1834 par Jean-Charles Peltier. C’est sur ce principe que fonctionnent les modules Peltier du commerce, qui utilisent aujourd’hui des matériaux semi-conducteurs.
Les puissances thermiques de réfrigération de ces modules vont de 1 W à quelques centaines de W. Elles sont donc compatibles avec la puissance thermique requise pour refroidir la canette. Les modules de puissance nécessitent cependant l’emploi de courants de forte intensité, de l’ordre de la dizaine d’ampères.
Faute de temps, nous n’avons pas pu explorer cette piste qui présenterait l’avantage d’être une solution portative. Nous nous interrogeons notamment sur le temps nécessaire pour atteindre le régime de fonctionnement d’un tel module. Ainsi que sur l’efficacité du transfert thermique avec la canette (contact solide/solide).
À ce sujet on pourra consulter les ressources sur l'effet thermoélectrique :
- « Chaleur et Nanotechnologies : la Thermoélectricité », une conférence de Sébastien Volz ;
- « Thermoélectricité : généralités, applications et conception des générateurs thermoélectriques », une conférence de Daniel Champier.
Effet magnétocalorique
Certaines substances magnétiques (métaux et céramiques comme MnAs1-X,Sbx) qui ont été aimantées par un champ magnétique se refroidissent lors du processus de désaimantation (quand on supprime le champ magnétique). Cet effet a été découvert en 1881 dans le fer par le physicien allemand E. Warburg. Le premier réfrigérateur conçu sur ce principe a été inventé en 1976 par Brown qui utilisait la désaimantation cyclique du gadolinium pour un abaissement de température de −44°C.
Cette solution a été écartée par notre partenaire.
2. La solution de refroidissement retenue
2.1 Principe
À l’issue de cette première phase de recherche, nous avons défini les propriétés du thermostat recherché. Il doit être :
- bon conducteur thermique pour évacuer efficacement la chaleur prélevée à la canette. De ce point de vue, les gaz sont moins efficaces que les liquides ou les solides car moins denses. Dans le cas des solides, il faudrait s’assurer d’un contact parfait entre le solide et la canette alors qu’avec un liquide, le contact est nécessairement parfait.
- le plus froid possible. En effet, le transfert thermique est d’autant plus efficace que la différence de température entre le thermostat et la canette est grand. Plus précisément, la puissance thermique est proportionnelle à la différence de température entre la canette et le thermostat d’après la loi de Newton (voir [annexe])
- de grande capacité thermique de façon à limiter son réchauffement et maintenir une différence de température importante entre le thermostat et la canette.
- liquide pour bénéficier de l’effet d’agitation qui favorise le transfert thermique (en effet, l'agitation permet de maintenir de part et d’autre de la paroi de la canette une différence de température supérieure à celle que l’on aurait sans agitation).
Nous avons alors retenu la solution de refroidissement suivante : l'utilisation d’un réfrigérant liquide préalablement refroidi par un congélateur à −18°C. L’utilisation d’un liquide, de capacité thermique élevée, permet de limiter le réchauffement du réfrigérant et de bénéficier de l’effet d’agitation. En revanche, cela nécessite d’utiliser un liquide réfrigérant qui se solidifie en-dessous de −18°C.
Nous nous sommes ainsi orientés vers le mélange eau-éthanol dont la température de solidification dépend du pourcentage massique d’éthanol comme le montre la courbe de la figure 4 (figure extraite de l’encyclopédie en ligne Wikipédia) :
Nous choisissons de travailler avec des mélanges réfrigérants dont le pourcentage massique en éthanol est de 40%, ce qui assure une température de solidification inférieure à −30°C tout en limitant la consommation d’éthanol.
2.2 Résultats expérimentaux
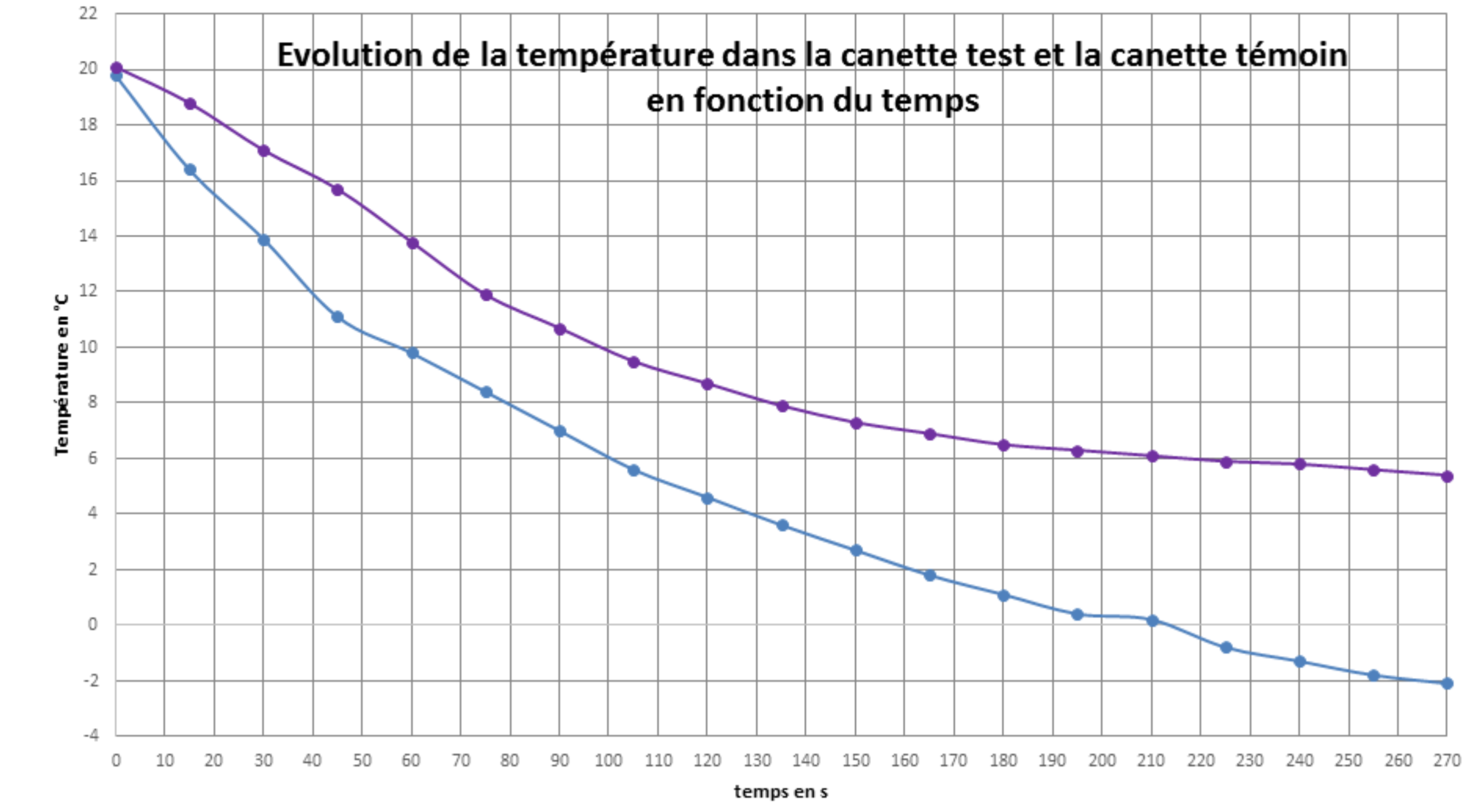
Pour tester la solution retenue, nous avons mis en place le protocole expérimental suivant : la canette test est placée au congélateur en même temps qu’une canette témoin. Nous mesurons les températures au centre des deux canettes en fonction du temps comme le montre la figure 5.
Différents paramètres ont été testés dont le volume du réfrigérant et l'agitation de l’intérieur de la canette.
Nous présentons ci-dessous un résultat d’expérience :
- la canette test est placée au congélateur dans 425 mL de réfrigérant dont la température initiale est de −28°C. L’intérieur de la canette est agitée mécaniquement. La température au centre de la canette est mesurée en fonction du temps.
- la canette témoin est placée dans le même volume de réfrigérant mais sans agitation de l’intérieur de la canette. De la même manière la température est mesurée en fonction du temps.
Nous obtenons les courbes de la figure 6.
Le processus de refroidissement est particulièrement efficace puisque nous atteignons avec agitation 5°C en 110 s ! La puissance moyenne de réfrigération est de 198 W ! Et à ce stade, le défi que nous nous étions lancé est relevé ! Notons que sans agitation, la canette témoin n’atteint pas 5°C en moins de trois minutes.
3. Optimisation du réfrigérant
Comment optimiser le réfrigérant et son pouvoir de réfrigération ? Pour répondre à cette question, il faut se pencher sur l’aspect théorique de la physique des transferts thermiques.
3.1 Aspect théorique
Le transfert thermique entre le réfrigérant et la canette est régi par la loi de Newton (voir [annexe]). La puissance thermique prélevée à la canette est donnée par :
P = h × S × (Tréfrigérant - Tcanette)
où h (Wm-2 K-1) est un coefficient d’échange caractéristique de l’interface canette/réfrigérant et S la surface d’échange entre la canette et le réfrigérant.
Il est à noter que la loi de Newton est empirique et aucune valeur de h n'est tabulée (on trouve des valeurs pour certaines géométries). En particulier, elle dépend de la convection du fluide.
Pour augmenter, la puissance thermique, on peut donc :
- augmenter la surface d’échange : la surface de la canette étant fixée, nous avons pensé ajouter des ailettes de refroidissement à la canette. Cependant, des tests réalisés ont montré un effet contre productif des ailettes par rapport à l’objectif visé.
- augmenter la valeur de h : c’est le rôle de l’agitation. En effet, le coefficient d’échange h est plus élevé en présence d’agitation. Cela se comprend facilement : l’agitation permet d’homogénéiser les températures dans le réfrigérant et la canette et de maintenir une différence de température importante de part et d’autre de la paroi de la canette de façon à maximiser le transfert thermique.
augmenter la différence de température Tréfrigerant −Tcanette. On peut penser augmenter le volume du réfrigérant. En effet, plus le volume du réfrigérant est grand, plus le réchauffement du réfrigérant est limité. Le réfrigérant reste efficace plus longtemps. D’un point de vue énergétique, pour refroidir 330 mL d’eau de 20°C à 5°C, il faut un volume équivalent de réfrigérant qui passe de −20°C à −5°C. Ainsi le volume minimal de réfrigérant est d’environ 330 mL. Il faut néanmoins trouver un compromis entre puissance thermique et encombrement du dispositif expérimental.
Nous avons développé une autre solution originale pour limiter le réchauffement du réfrigérant comme nous allons le voir dans le paragraphe suivant.
3.2 Ajout d'un absorbeur de chaleur
En vue d'optimiser la réfrigération, nous allons essayer de maintenir la température du réfrigérant constante. Il faut donc évacuer la chaleur que le réfrigérant prélève à la canette ou l’absorber ! L’idée originale que nous avons trouvée est la suivante : utiliser la fusion du mélange eau-éthanol pour absorber la chaleur. Comme nous l’avons vu lors des expériences préliminaires, les changements d’état sont particulièrement efficaces d’un point de vue énergétique. En jouant sur la composition en éthanol du mélange eau-éthanol, nous pouvons choisir sa température de fusion. Ainsi, pour une fraction massique en éthanol de 30%, la température de fusion est de −20°C d’après la figure 4.
Pour tester cette idée, nous réalisons l’expérience suivante :
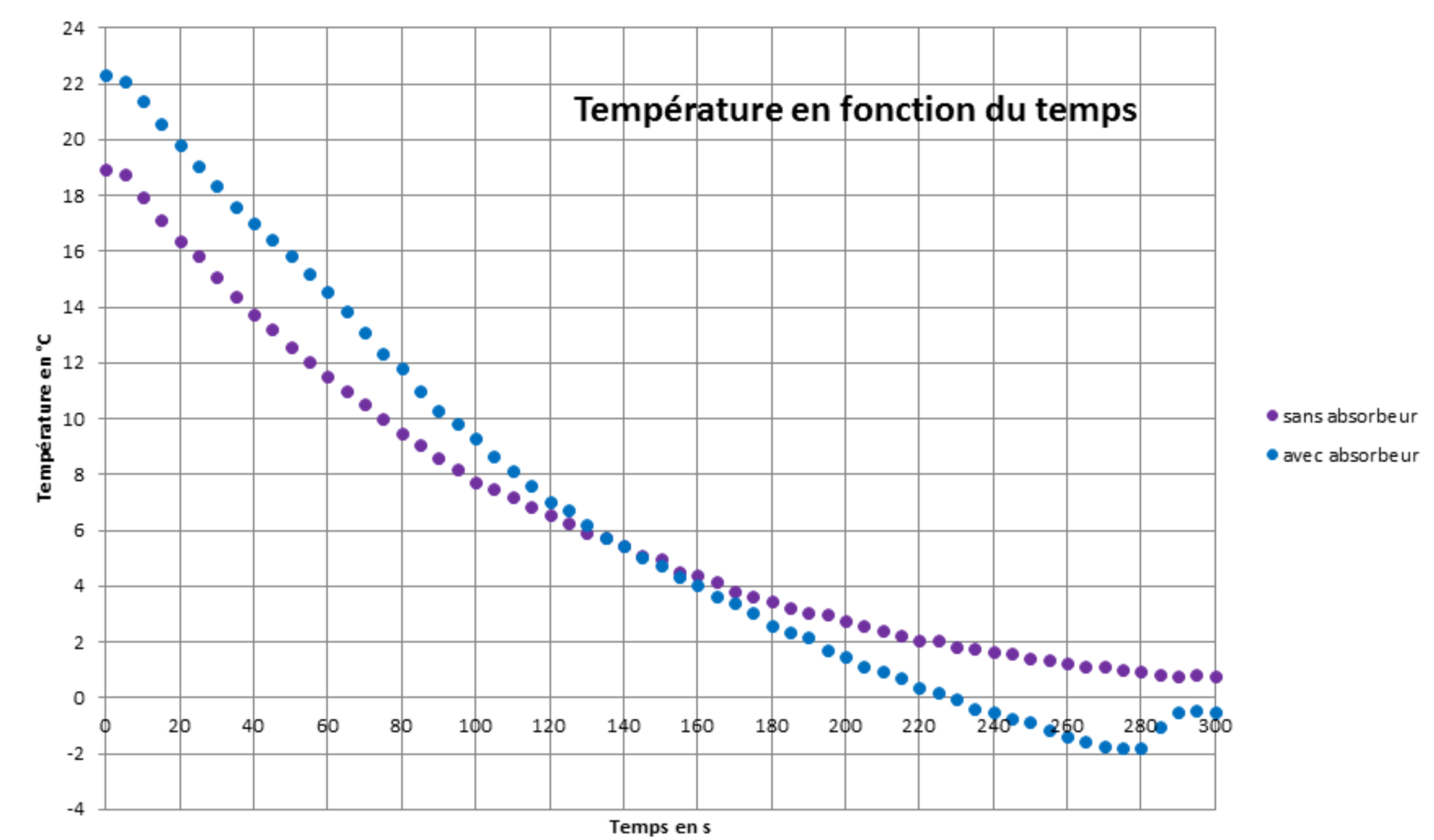
La canette est plongée (à la date t = 0) dans un volume V = 400 mL de réfrigérant liquide à −28°C entouré de 900 mL de réfrigérant solide à la même température et séparé par une paroi en aluminium (bon conducteur thermique). Le pourcentage massique du réfrigérant solide a été choisi pour qu’il fonde vers -20°C. L’intérieur de la canette et le réfrigérant liquide sont agités. La température de la canette est mesurée au cours du temps à l’aide d’un système d’acquisition ainsi que celle du réfrigérant (figure 7). La même expérience est réalisée en remplaçant le réfrigérant solide par un réfrigérant liquide de même volume.
Notons l’évolution du protocole expérimental. L’expérimentation est réalisée en dehors du congélateur et à la température ambiante. Certes les pertes thermiques avec l’air ambiant sont plus importantes mais cela nous a permis d’interfacer les thermomètres d’une part et d’autre part d’agiter l’intérieur de la canette et le réfrigérant.
Nous obtenons les courbes de températures suivantes (figure 8) qui montrent l’effet positif de l’absorbeur sur le refroidissement : la vitesse de décroissance de la température diminue au cours du temps dans l’expérience sans absorbeur alors qu’elle reste sensiblement constante au début de l’expérience avec absorbeur. La température de 5°C est atteinte plus rapidement en présence d’absorbeur et ce malgré une température initiale supérieure.
Nous notons au passage l’apparition d’un phénomène de surfusion dans l’expérience réalisée avec l'absorbeur qui se manifeste à partir de 230 s et qui cesse à 280 s.
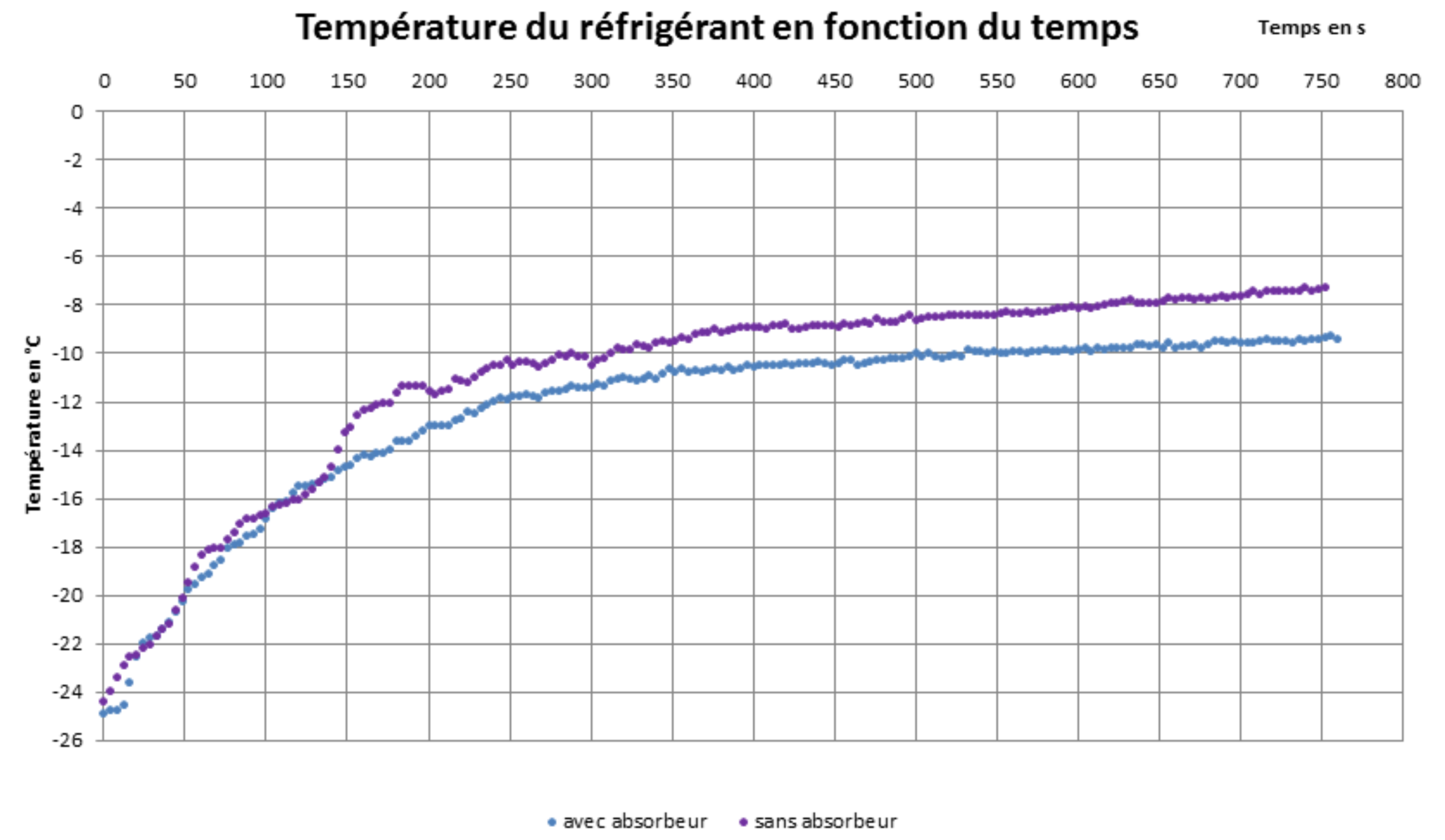
L’effet de l’absorbeur est confirmé par la courbe montrant l’évolution de la température du réfrigérant en fonction du temps (figure 9) : l’absorbeur limite le réchauffement du réfrigérant.
4. Conclusion
Nous nous étions lancés comme défi de refroidir une canette en moins de 3 minutes. Ce défi nous a conduit sur le chemin de la physique des transferts thermiques dont nous avons pu améliorer notre compréhension. Nous avons mis au point une solution de réfrigération simple et efficace mettant en jeu des puissance thermiques moyennes de l’ordre de 200 W et qui pourrait trouver des applications dans les besoins de réfrigération rapides.
Il resterait à développer un prototype utilisable au quotidien qui permette de maintenir la canette au sec et étudier l’effet de l’agitation sur les boissons gazeuses.. Le principe pourrait être intégré aux futurs réfrigérateurs ou mis à profit dans les distributeurs de boissons réfrigérées qui, plutôt que de refroidir un ensemble de canettes, se limiteraient à refroidir l’équivalent du volume d’une canette. Cela représenterait un gain énergétique substantiel compte-tenu des enjeux énergétiques et écologiques actuels.
Nous remercions vivement M.Nicolle (Directeur Agile@RD Paris-Saclay Eco-système) et son équipe dont C. Delboux (Responsable Méthodes Agiles) pour avoir pris le temps de nous recevoir à plusieurs reprises sur le site de Air Liquide (Jouy en Josas, Yvelines) et pour les échanges fructueux que nous avons eu ensemble. Nous remercions également nos professeurs M. Jouan et M. Chriqui pour nous avoir guidés dans la réalisation de ce projet.
5. Références
- [1] Mélanges réfrigérants, wiki.scienceamusante.net
- [2] Solidification fractionnée, Wikipedia RTE
6. Un exercice pour aller plus loin
Les encadrants de ce projet proposent un exercice pour poursuivre le sujet : Modélisation du transfert thermique entre la canette et le réfrigérant et aspect expérimental.
Annexe sur la loi de Newton
Dans cette annexe nous cherchons à valider la loi de Newton dans le cas de la réfrigération de notre canette :
P = h × S × (Tréfrigérant - Tcanette)
Nous réalisons l'expérience suivante :
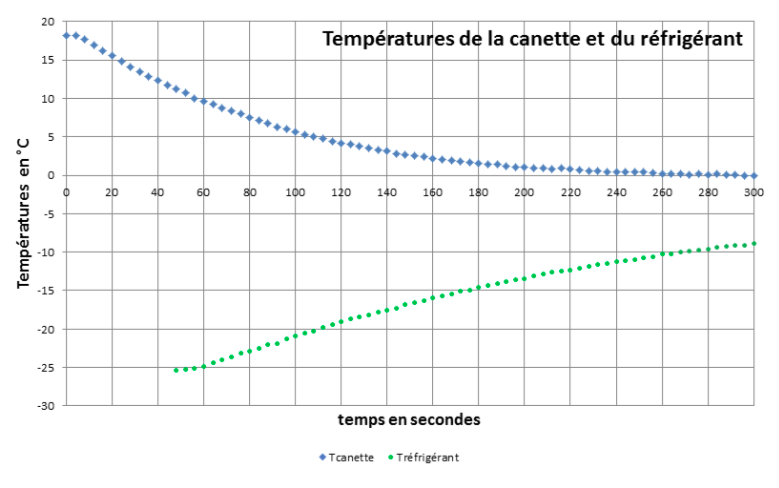
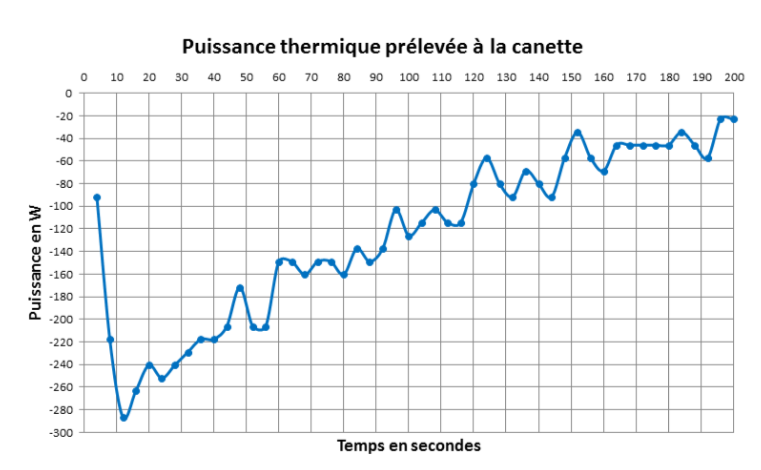
La canette est plongée (à la date t = 0) dans un volume V = 480 mL de réfrigérant à -28°C. L'intérieur de la canette et le réfrigérant sont agités ce qui permet entre autre d’homogénéiser les températures du réfrigérant et de la canette. Les températures de la canette et du réfrigérant sont mesurées au cours du temps à l'aide d'un système d'acquisition de données. Nous obtenons les courbes de températures de la figure 10.
L'exploitation de la courbe de température de la canette nous a permis de tracer l'évolution de la puissance thermique prélevée à la canette en fonction du temps. En effet, la puissance thermique se calcule par la relation :
Où est la capacité thermique de la canette (contenu + paroi) et la dérivée de la température en fonction du temps que nous évaluons à partir de nos mesures. Cette formule suppose que la température de la canette soit homogène, ce qui est assuré par l’agitation de l'intérieur de la canette.
Nous obtenons la courbe de puissance thermique suivante (figure 11) où P est inférieure à 0 car la canette cède de la chaleur au réfrigérant.
La courbe met en évidence une puissance maximale de réfrigération de 300 W !
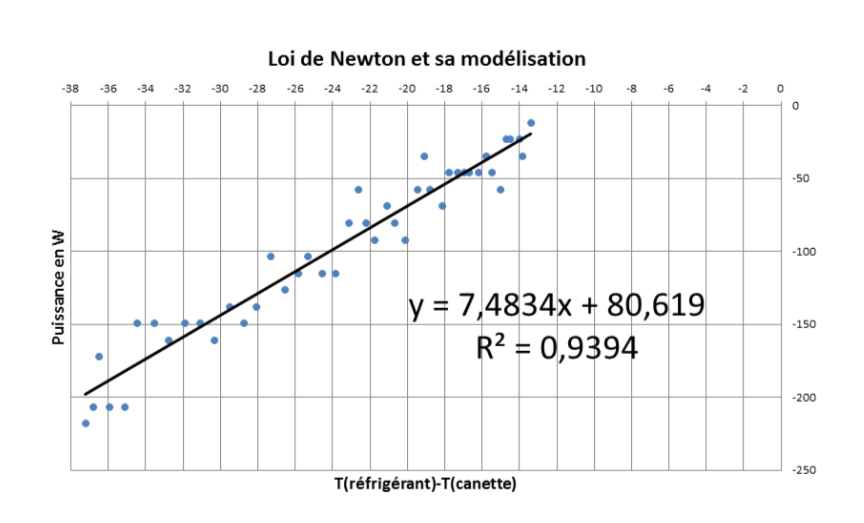
Pour finir, nous traçons la courbe représentant l'évolution de la puissance thermique prélevée à la canette en fonction de la différence de température Tréfrigérant-Tcanette afin de vérifier la loi de Newton :
P = h × S × (Tréfrigérant - Tcanette)
Nous obtenons alors la courbe figure 12.
Nous obtenons bien une droite mais dont l'ordonnée à l'origine non nulle est en désaccord avec la loi de Newton.
Comment interpréter cet écart ?
Une ordonnée à l'origine positive correspond à un apport de chaleur à la canette. Nous avons d'abord pensé à l'influence de l'air ambiant qui fournit de la chaleur à la canette lors du processus de refroidissement. Nous avons donc refait l'expérience avec une canette munie d'un couvercle de façon à limiter les échanges avec l'air ambiant. L'ordonnée à l'origine reste positive et d'une valeur comparable à celle trouvée précédemment.
La solution au problème vient de la solidification qui libère de la chaleur dans la canette. Proche de la paroi interne, il existe une couche limite dans laquelle la vitesse du fluide décroît jusqu'à s'annuler au contact de la paroi. Au niveau de la paroi, l'eau gèle malgré l'agitation à l'intérieur de la canette. Il faudrait donc écrire le bilan énergétique de la canette et son contenu sous la forme :
où est le transfert thermique nécessaire pour provoquer la fusion d'1kg d'eau (c'est aussi la chaleur libérée par la solidification d'1kg d'eau) et le taux de production de glace au niveau des parois que l'on peut évaluer grâce à l'ordonnée à l'origine :
= 0,24 g.s-1
Cette hypothèse est confirmée par l'observation expérimentale d'une couche de glace à l'intérieur de la canette au niveau des parois en fin de l'expérience.
Ce phénomène pourrait être mis à profit pour garder le contenu de la canette froid plus longtemps.
Pour citer cet article :
Comment réfrigérer une cannette en moins de trois minutes, mai 2021. CultureSciences Physique - ISSN 2554-876X, https://culturesciencesphysique.ens-lyon.fr/ressource/cool-can.xml





![Température de solidification d’un mélange eau-éthanol en fonction du pourcentage massique d’éthanol ([2])](https://culturesciencesphysique.ens-lyon.fr/images/articles/coolcan/fig4.png)