Activer le mode zen
Ressource au format PDF
Mots-clés
- intelligence artificielle
- modélisation
- machine learning
- deep learning
Classification
Introduction à l’apprentissage profond (deep learning) de l'intelligence artificielle
11/10/2021
Résumé
Dans ce document, nous donnons une courte introduction à l’apprentissage par réseaux de neurones, spécialement pensée pour les enseignants du secondaire de physique-chimie en charge des nouveaux enseignements en « Enseignement scientifique ». Après une présentation historique des travaux et des applications, les principes de base et une discussion sur l’impact sociétal de ces méthodes est proposé ainsi que des indications vers des ressources pédagogiques complémentaires.
Table des matières
- Introduction
- 1. Historique des travaux sur l'intelligence artificielle et révélation des possibilités de l'apprentissage profond
- 2. Exemples d'applications de l'apprentissage profond
- 3. Principes et généralités sur l’apprentissage automatique supervisé
- 4. Principes de l'apprentissage profond
- 5. Avantages et inconvénients par rapport à l’apprentissage automatique traditionnel
- 6. Impact sociétal
- 7. Ressources complémentaires
Introduction
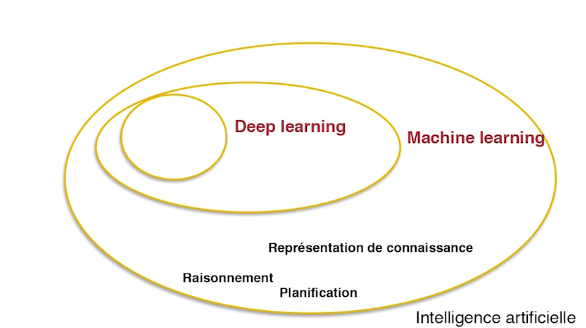
Le deep learning ou apprentissage profond est un sous-domaine du machine learning ou apprentissage machine, sous-domaine de l'intelligence artificielle, figure 1.
Par intelligence artificielle on comprend l'acte de faire reproduire par des machines des tâches qui sont jugées comme complexes par les humains, typiquement : faire raisonner une machine, apprendre à une machine la planification de tâches, ou encore apprendre à une machine à représenter des connaissances d'une manière structurée…
Le deep learning ou apprentissage profond, regroupe actuellement les méthodes les plus efficaces et les plus performantes appliquées dans la communauté de l'apprentissage automatique.
1. Historique des travaux sur l'intelligence artificielle et révélation des possibilités de l'apprentissage profond
Les méthodes d'apprentissage machine ne sont pas récentes mais datent des années 60. Dès les débuts de l'informatique, les pionniers avaient imaginé des systèmes et des principes d'apprentissage à base de réseaux de neurones. Les bases de ce fonctionnement ont été développés sur des machines depuis 1986 avec notamment les travaux de Geoffrey Hinton, universitaire canadien (figure 2 à gauche). Jusqu'en 2006, d'autres méthodes ont pris le dessus et les méthodes d'intelligences artificielles par réseaux de neurones ont été mises de côté. C'est grâce à une idée de Geoffrey Hinton que ces techniques sont revenues à la mode.
En 2012, Geoffrey Hinton et son équipe nommée "SuperVision" participent à un concours de traitement d'images sur la base de données ImageNet. Le concours consiste à traiter le contenu d'un million d'images, dont quelques exemples sont présentés figure 2 à droite.
Le challenge ILSVRC (ImageNet Large Scale Visual Recognition Challenge) porte sur la reconnaissance d'objets par une machine dans ce pool d'un million d'images ! C'est-à-dire qu'il faut que la machine soit capable de reconnaître si une coccinelle est présente dans une image ou si l'on voit de la neige, etc. Il faut finalement que la machine réalise une classification du contenu d'images très diverses. En amont, toutes ces images ont été finement annotées manuellement. Les résultats du traitement des images par les machines des différents compétiteurs sont ensuite comparés aux annotations initiales. Le but du concours consiste à déterminer quel est l'algorithme qui se rapproche le plus de "la vérité" annotée par des humains.
L'idée géniale de Geoffrey Hinton est l'utilisation de cartes graphiques d'ordinateurs pour faire ses calculs. En effet, les cartes graphiques, bien connues des amateurs de jeux vidéos, sont capable d'effectuer des calculs énormes très rapidement. Il se trouve que grâce à l'utilisation des cartes graphiques et de son algorithme d'apprentissage profond, l'équipe de Geoffrey Hinton gagne très largement devant l'Université de Tokyo, d'Oxford, l'équipe Xerox/INRIA, …
Par la suite, en 2013, Geoffrey Hinton, rejoint l'entreprise Google, tout en restant professeur à l'université de Toronto. Les pionniers de ce domaine de l'intelligence artificielle ont à peu près tous suivi ce chemin, car c'est principalement les grandes entreprises privées qui disposaient d'une grande quantité de données, leur permettant d'améliorer encore les méthodes d'apprentissage profond. Par exemple, le français Yan LeCun a rejoint l'entreprise Facebook. À partir de 2012, dans les concours de traitement d'images, les algorithmes employés sont issu de l'apprentissage profond.
Médiatiquement, dans ces années, on commence à beaucoup entendre parler de l'intelligence artificielle et de l'apprentissage profond. En 2016, l'intelligence artificielle est encore mise en lumière lorsque, pour la première fois, une machine bat un humain au jeu de GO, jeu qui a une logique combinatoire encore plus importante que celle des échecs. Ces victoires de la machine sur l'homme découlent du fait qu'il y a, maintenant par rapport à quelques années en arrière, de plus grandes bases de données disponibles pour entraîner les machines et des moyens de calculs beaucoup plus rapides.
2. Exemples d'applications de l'apprentissage profond
Nous présentons ici quelques applications de l’apprentissage profond, en restant sur l'aspect image.
Comme nous venons de le voir, une machine peut classer le contenu d'images : reconnaître qu'il y a un chien, un léopard, etc. figure 3 à gauche. Ensuite, il est possible de regrouper des images de même contenu au sein d'une banque d'images. Par exemple, figure 3 à droite, la machine est capable de retrouver toutes les images dans lesquelles il y a une fleur violette ou des éléphants et de les regrouper ensemble.
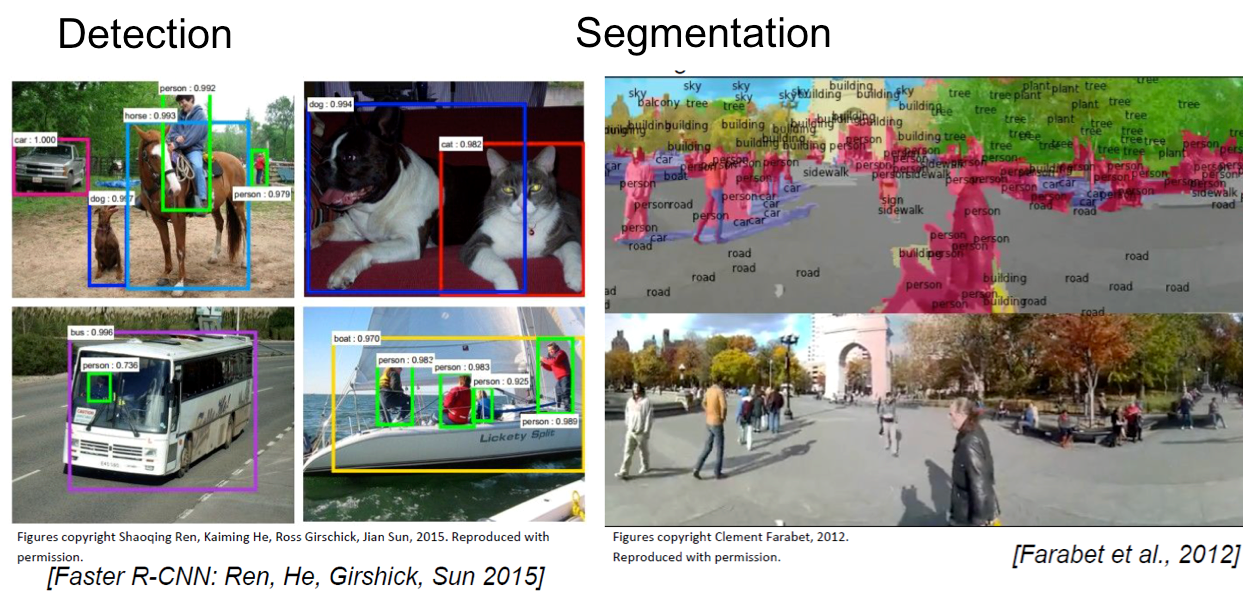
Il est encore possible d'aller plus loin dans la compréhension du contenu des images. On peut détecter des objets (figure 4 à gauche) et segmenter (ou détourer) les objets dans des scènes complexes. Un exemple est donné figure 4 à droite, où des humains marchant dans la rue sont précisément repérés. Cela s'avère d'ailleurs une fonction indispensable pour des projets de type véhicule autonome.
Dans le domaine de l'imagerie médicale, l'apprentissage profond peut aussi jouer un rôle de détection et prédiction. Par exemple, la figure 5a présente différentes images de grains de beauté bénins ou malins. Des travaux ont montré que la distinction a été réalisée avec une précision meilleure par la machine que par des experts, pas toujours tous unanimes. Ces méthodes affichent aussi de très bons résultats dans la détection de certains cancer dont le cancer du sein par mammographie.
L'apprentissage profond peut aussi être utilisé dans le domaine biologique pour suivre, par exemple figure 5b, les grands mammifères marins à l'aide de la vision satellite.
Une application plus fondamentale et encore en développement de l'intelligence artificielle est la possibilité de décrire sémantiquement une image, c'est-à-dire que la machine soit capable de produire un texte qui correspond au contenu de l'image. Par exemple, figure 6 : "il y a un chat assis dans une valise posée par terre".
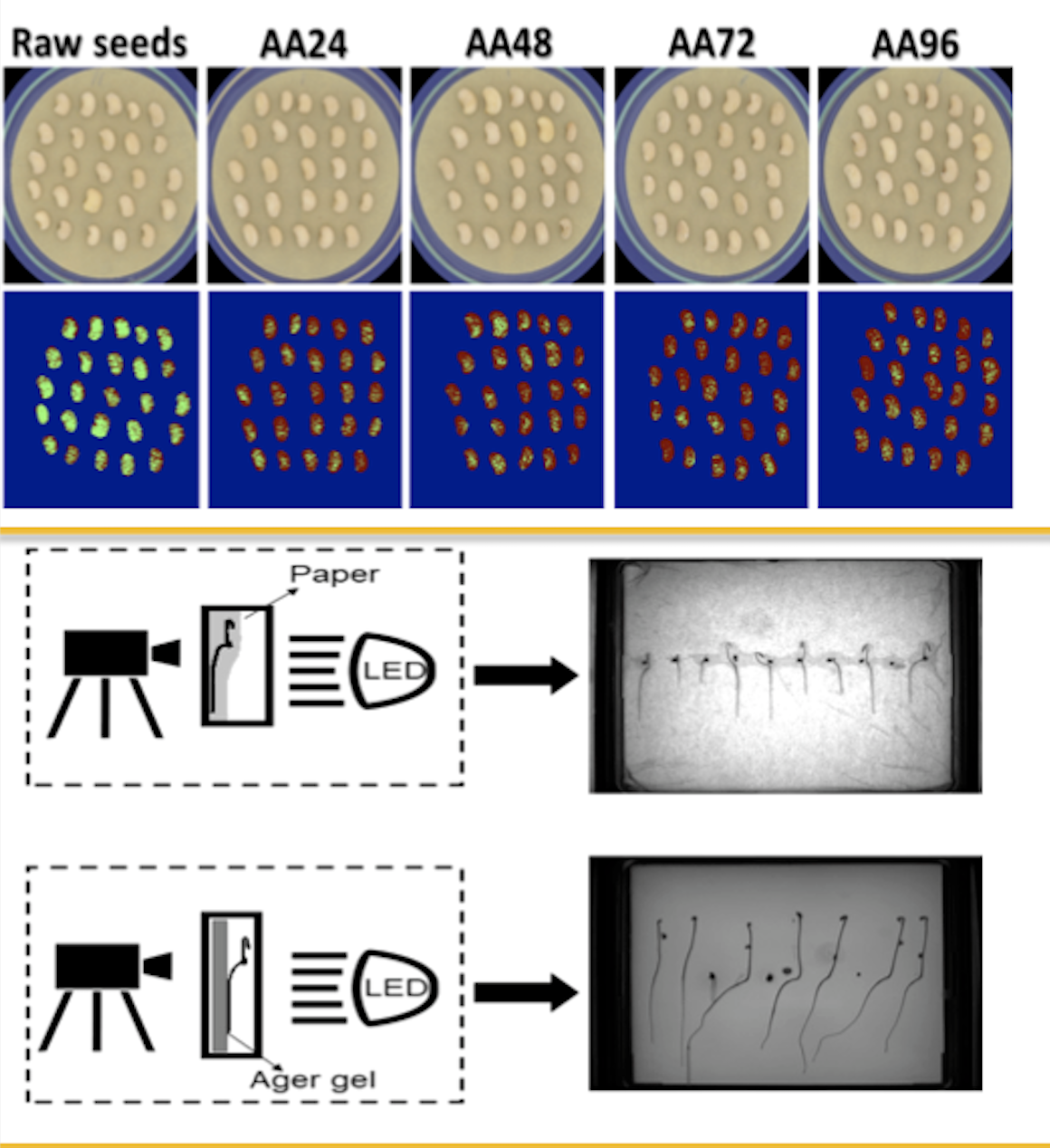
Dans le domaine de l'agronomie (figure 7) il est aussi possible de détecter si des graines sont viables ou non, de suivre la croissance des racines par rayons X, ou encore de détecter des mauvaises herbes sur des lits de mâche.
Nous venons de voir que les domaines d'application sont très nombreux et divers, nous proposons maintenant de voir un peu plus en détail le principe de ces méthodes d'apprentissage.
3. Principes et généralités sur l’apprentissage automatique supervisé
Nous rappelons d’abord les principes généraux du champ de l’apprentissage automatique, dont l’apprentissage profond est, comme nous venons de le voir, un sous-domaine. Nous nous concentrons ici sur le cas d’un algorithme de classification. D’autres tâches d’apprentissage automatique existent (segmentation, régression, système de recommandation, etc.) mais peuvent être dérivées à partir du cas de la classification.
Le but d’un algorithme de classification est d’associer de façon automatique une étiquette à un objet. Nous nous plaçons dans le domaine de la vision par ordinateur, où l’objet est une image et l’étiquette peut être par exemple un mot qui décrit le contenu dans l’image.
Initialement, l’apport principal de ces algorithmes était une accélération de cet étiquetage lorsque le nombre d’objets en faisait une charge trop fastidieuse pour des humains. Aujourd’hui, certains de ces algorithmes ont progressé au point d’obtenir des performances super-humaines sur certaines tâches. Nous nous limitons ici au cas des algorithmes dits supervisés, c’est-à-dire ceux qui sont entraînés sur un ensemble d’images dont les étiquettes sont connues.
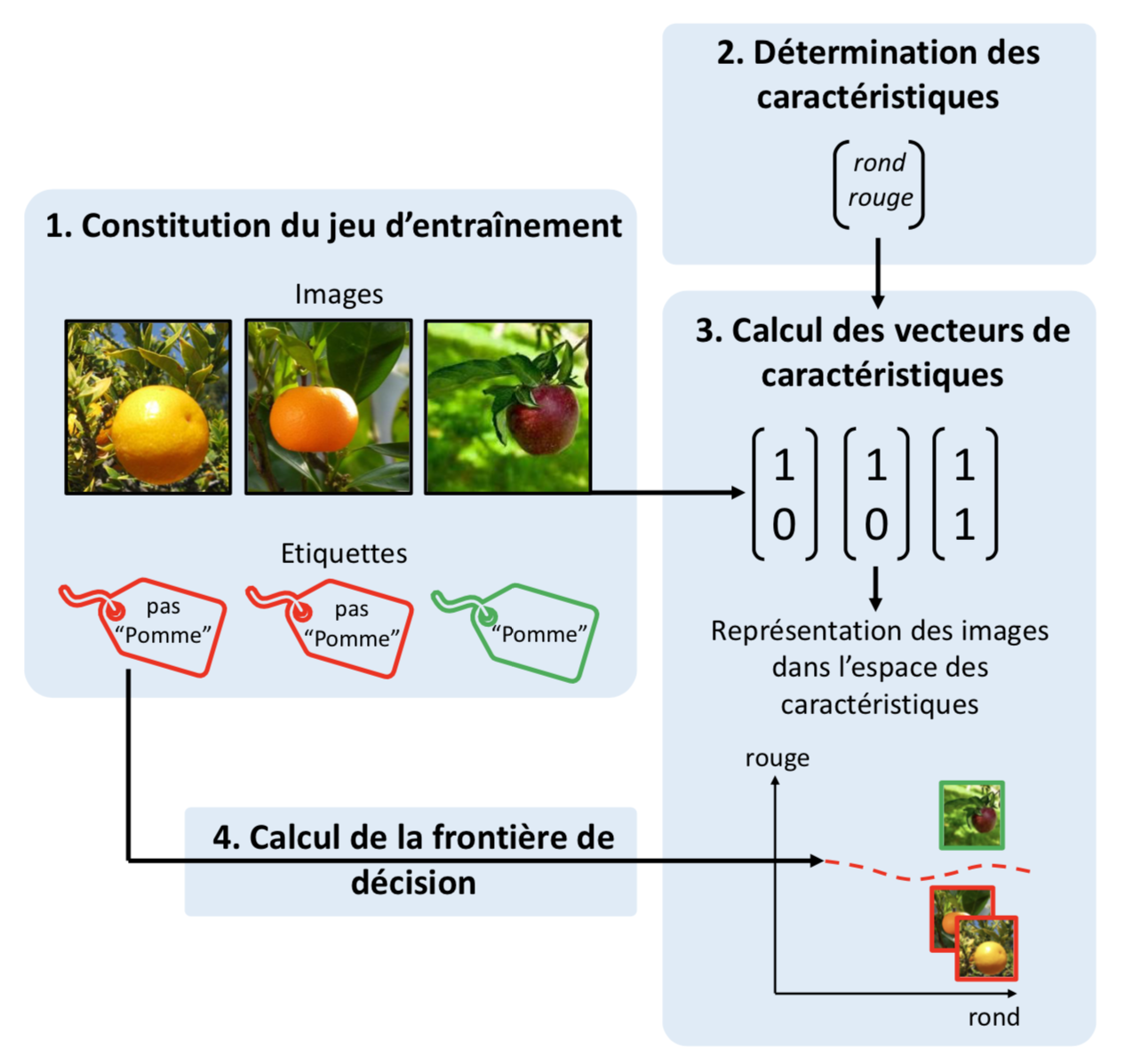
Nous détaillons à présent les étapes d’un tel apprentissage, illustrées en figure 8.
Nous considérons, pour illustration, une classification binaire où l’on cherche à déterminer la présence ou l’absence de pommes dans des images. Les étapes décrites sont valables pour n’importe quel algorithme d’apprentissage supervisé.
- Constitution d’un jeu d’entraînement : un ensemble d’images, dont les étiquettes sont connues, sont regroupées dans un jeu de données dit d’entraînement. On appelle annotation le processus d’attribuer des étiquettes aux images en premier lieu.
Détermination des caractéristiques : une caractéristique est une mesure que l’on fait sur les objets contenus dans l’image relativement à leur forme, leur couleur, leur texture, leur gradient, leur longueur, etc.
Dans l’application donnée en exemple, les caractéristiques retenues sont la présence de la couleur rouge (qui pourrait être calculée via un seuillage de couleur) et de formes rondes (qui pourrait être calculée via un algorithme de détection de forme telle que la transformée de Hough) dans l’image. Des caractéristiques plus élaborées ont été développées au fil des années, telles que des caractéristiques de textures d’Haralick ou les caractéristiques visuelles invariantes à l’échelle (Scale-Invariant Feature Transform en anglais, ou SIFT).
Calcul des vecteurs de caractéristiques : les caractéristiques sont calculées sur chaque image du jeu d’entraînement, qui sont à l’issue de cette étape, représentées chacune par un vecteur de caractéristiques.
Dans l’exemple de la figure 8, nous indiquons pour chaque caractéristique sa présence ou son absence dans l’image par une valeur binaire (1 ou 0). Nous pouvons alors nous représenter visuellement les images dans l’« espace des caractéristiques ». Cet espace a un nombre de dimensions égal au nombre de caractéristiques calculées. Dans cet exemple, on compte 2 dimensions (une pour la forme et une pour la couleur). Nous pouvons nous représenter dans cet espace chaque image comme un point dont la position est donnée par son vecteur de caractéristiques, et la couleur par son étiquette.
Calcul de la frontière de décision : les vecteurs de caractéristiques des images du jeu d’entraînement sont présentées à un algorithme d’apprentissage avec les étiquettes associées.
Le but attendu de cette étape est de faire le lien entre les valeurs des caractéristiques des images et les étiquettes qui leur sont associées. Visuellement, le but de l’algorithme est de trouver l’hyperplan (pour un espace à n dimensions. Ici avec simplement 2 dimensions cela consiste en un une droite) qui sépare dans cet espace de caractéristiques les groupes d’objets avec la même étiquette, que l’on appelle la frontière de décision (ligne pointillée rouge en bas à droite de la figure 8). Si les caractéristiques sont bien choisies, que le jeu d’entraînement est assez divers et que la capacité de l’algorithme, c’est-à-dire la complexité de l’hyperplan qu’il peut définir, sont suffisants pour la classification considérée, alors l’algorithme convergera vers cet hyperplan.
Une fois l’algorithme entraîné, il peut être utilisé pour réaliser des prédictions, c’est-à-dire des propositions d’étiquettes sur un jeu d’images qu’on ne lui a jamais présenté. Visuellement, cela correspond à placer un point dans l’espace des caractéristiques et de lui attribuer une étiquette en fonction de sa position par rapport à la frontière de décision.
L’exemple d’algorithme d’apprentissage automatique supervisé le plus simple est celui des « k plus proches voisins ». On présente d’abord à l’algorithme les vecteurs de caractéristiques et les étiquettes du jeu d’entraînement. Puis, pour déterminer l’étiquette d’un nouvel élément, on calcule les k plus proches éléments parmi ceux du jeu d’entraînement. Plusieurs possibilités existent pour calculer cette distance, la plus populaire étant la distance euclidienne entre les vecteurs de caractéristiques. L’étiquette la plus représentée parmi ces plus proches voisins est attribuée à ce nouvel élément. Afin d'illustrer cet exemple, on pourra se reporter à : l'extrait de la vidéo, proposée dans la section 7 au sujet de la frontière de décision, des voisins et des erreurs possibles (à partir de 6 min15).
En pratique, lorsque l’on souhaite entraîner un algorithme de classification à partir d’une jeu, on sépare ce jeu en plusieurs sous-ensembles que l’on appelle des « blocs » (sets en anglais). On conserve typiquement entre 60 et 80% des images comme bloc d’entraînement, et on utilise le reste comme bloc dit de test. Ce bloc ne sert pas à entraîner l’algorithme, mais est utilisé pour évaluer les performances de ce dernier sur des images hors de son bloc d’entraînement. La performance obtenue sur le bloc de test agit donc comme un indicateur de la performance de l’algorithme en déploiement sur de nouvelles images.
De plus, pour beaucoup de ces algorithmes, il est nécessaire de fixer des hyperparamètres, c’est-à-dire des paramètres concernant le fonctionnement de l’algorithme lui-même. Par exemple, la valeur k et la métrique de distance sont les hyperparamètres de l’algorithme des « k plus proches voisins ». Pour fixer ces hyperparamètres, on a souvent recours à une autre division du jeu, que l’on appelle bloc de validation. L’idée est alors, pour chaque combinaison d’hyperparamètres que l’on souhaite tester, d’effectuer un entraînement sur le bloc d’entraînement, puis d’effectuer une prédiction sur le bloc de validation. La performance atteinte sur ce bloc est alors un indicateur de la qualité des hyperparamètres pour cette tâche. L’ensemble d’hyperparamètres menant à la performance de validation la plus élevée est alors conservé. Pour entraîner un algorithme d’apprentissage, il est donc très courant de diviser le jeu d’images disponible en trois blocs : entraînement, validation et test.
4. Principes de l'apprentissage profond
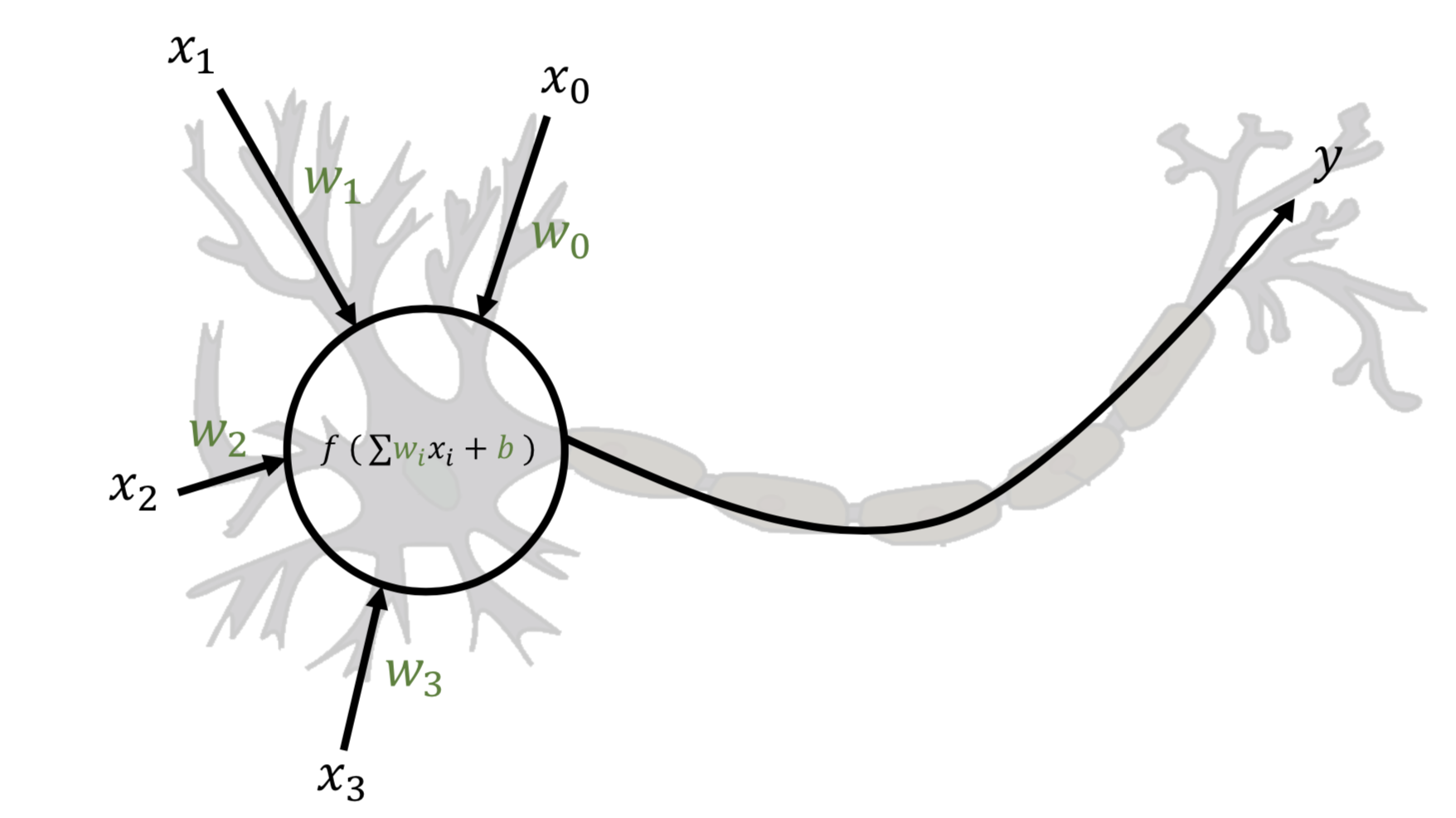
L’apprentissage profond est un paradigme d’apprentissage automatique inspiré de l’anatomie du cerveau humain. Cet apprentissage est associé à une structure algorithmique que l’on appelle un réseau de neurones. Le neurone biologique est une cellule complexe, mais seul son fonctionnement basique a servi d’inspiration au neurone informatique. Le parallèle entre neurone biologique et neurone informatique est illustré figure 9.
Un neurone biologique reçoit des signaux électriques d’autres neurones en amont via des points d’entrées (x0, x1, x2 et x3). Ces signaux sont accumulés à l’intérieur du corps du neurone, et si la somme de ces signaux dépasse un certain seuil, le neurone s’active et envoie à son tour un signal à des neurones en aval. Un neurone informatique approxime ces principes. Il accepte en entrée un nombre fixe de nombres réels (représentant les signaux des neurones en amont) et produit en sortie (y) une valeur réelle (représentant le signal envoyé aux neurones en aval). Cette sortie est calculée à partir des entrées via l’équation :
qui représente l’accumulation de signaux électriques.
Les entrées sont multipliées par des valeurs wi que l’on appelle les poids, qui représentent la force de la connexion entre ce neurone et les neurones en amont. La fonction f est une fonction dite d’activation. Il s’agit d’une fonction non-linéaire croissante.
Les premières implémentations de réseaux définissaient f comme une fonction seuil : f renvoie 1 si son argument est strictement positif et 0 sinon, mais d’autres fonctions furent proposées au fil des années comme la fonction unité linéaire rectifiée (Rectified Linear Unit en anglais, ou ReLU). Cette fonction représente l’activation du neurone si celui-ci a accumulé suffisamment de potentiel électrique. La valeur b, que l’on appelle le biais, représente l’appétence ou la résistance du neurone à s’activer. Les poids et le biais (souvent désignés collectivement sous le nom de « poids ») sont les paramètres du neurone : ce sont ces valeurs qui sont modifiées au cours d’un entraînement.
Un neurone informatique peut constituer à lui seul le support d’un algorithme d’apprentissage pour certaines tâches bien définies. En constituant un jeu d’entraînement composé de paires d’entrées réelles et des sorties binaires attendues, et en présentant séquentiellement ces exemples au neurone, il existe un algorithme d’entraînement qui définit comment modifier les poids de celui-ci afin de converger vers la classification attendue.
Cependant, la capacité d’un neurone unique est trop faible pour qu’il soit appliqué ailleurs que sur des cas jouets. Les algorithmes d’apprentissage profond sont basés sur des ensembles de neurones que l’on appelle des réseaux. On appelle « architecture » la structure selon laquelle les neurones sont reliés entre eux. Les premières architectures s’appelaient les perceptron multi-couche (Multi-Layer Perceptron en anglais, ou MLP). Dans un MLP, les neurones sont connectés à la fois parallèlement et séquentiellement selon une organisation en couches (figure 10).
La première couche est constituée d’un certain nombre de neurones qui prennent en entrée les données. Les sorties des neurones de cette couche servent d’entrée à une deuxième couche de neurones, et ainsi de suite, jusqu’à une dernière couche dont on identifie la sortie à proposition faite par le réseau pour l’étiquetage de l’entrée. Cette structure en couches est inspirée de l’architecture neuronale du cerveau humain.
La phase d’entraînement d’un réseau se déroule de la façon suivante. Tous les paramètres sont initialisés aléatoirement. Un exemple issu du bloc d’entraînement est présenté au réseau. Le réseau calcule une sortie, que l’on compare à l’étiquette et on en calcule une mesure de performance. Un algorithme que l’on appelle la rétro-propagation d’erreur permet alors de calculer la contribution de chaque poids du réseau à la sortie proposée et donc à la performance pour cet exemple. La connaissance de ces contributions permet de connaître la forme locale de la fonction de performance en fonction des valeurs des poids. Une itération d’un algorithme d’optimisation est alors appliquée pour modifier les valeurs des poids afin d’améliorer la performance du réseau sur cet exemple. Un nouvel exemple est présenté et le cycle recommence. L’entraînement se poursuit jusqu’à ce que la performance se stabilise ou selon d’autres critères d’arrêt. On dit alors que le réseau a convergé ou bien est entraîné. Le réseau peut ensuite être utilisé en prédiction pour produire des étiquettes sur des données qu’on ne lui a jamais présentées.
5. Avantages et inconvénients par rapport à l’apprentissage automatique traditionnel
5.1 Avantages
Par rapport à d’autres structures algorithmiques, les réseaux de neurones ont deux grands avantages :
Premièrement, leur structure basée sur l’empilement de fonctions non-linéaires leur octroie une énorme capacité. Il a été montré qu’un réseau avec deux couches seulement peut représenter n’importe quelle fonction mathématique liant des entrées et une sortie. Pour des raisons d’entraînement et de capacité de calcul, les architectures modernes comprennent toutefois un plus grand nombre de couches.
Deuxièmement, les réseaux agissent à la fois comme algorithmes de classification et comme extracteurs de caractéristiques. En effet, ce sont, dans la grande majorité des cas, les données elles-mêmes (les valeurs des pixels dans le cas des images) qui sont fournies en entrée à un réseau et non des caractéristiques prédéfinies (comme dans l’exemple de la figure 8).
Les algorithmes de rétro-propagation et d’optimisation permettent d’exploiter la grande capacité du réseau en contraignant les poids des réseaux vers un ensemble des valeurs qui mène à une bonne performance de classification : les caractéristiques sont apprises spécifiquement pour la tâche considérée. Les caractéristiques extraites, simples si on les considère dans les premières couches, se complexifient peu à peu au fil des opérations faites par les couches. C’est cette dimension de couches empilées, qui permet la création de caractéristiques complexes, à laquelle on fait référence lorsqu’on parle d’apprentissage « profond ». Cela mène à des caractéristiques qui peuvent être extrêmement raffinées et subtiles, bien plus que ce qu’un humain ou un algorithme d’extraction de caractéristiques classique peuvent réaliser.
5.2 Inconvénients
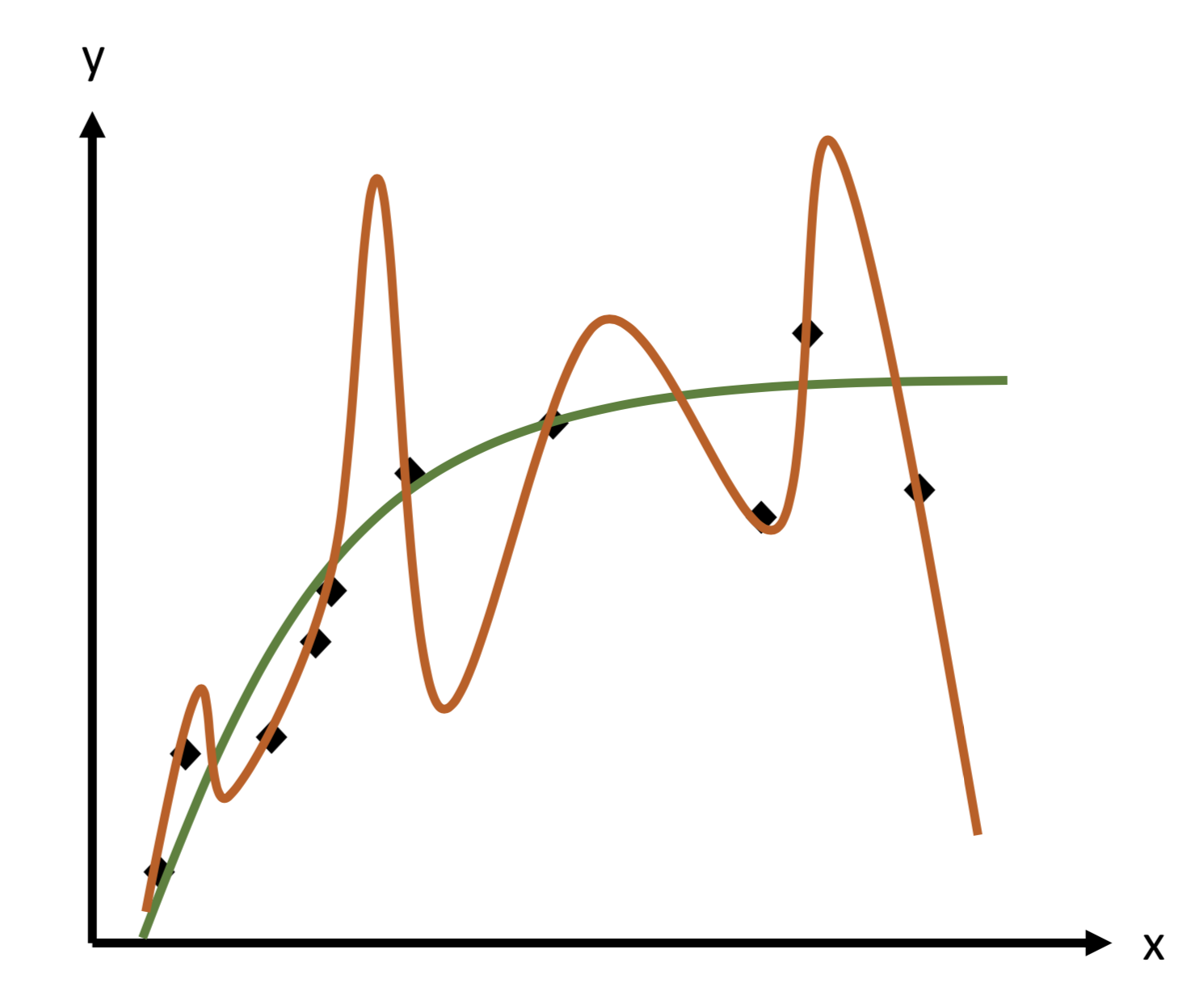
La grande capacité des réseaux peut entraîner cependant un grand inconvénient : le sur-apprentissage (overfit en anglais). Pour l’illustrer, plaçons-nous dans le cadre d’une application d’apprentissage automatique simple : la régression non-linéaire (figure 11). Considérons que nous avons n points d’entraînement qui sont des paires de nombres réels (xi, yi) et que nous souhaitons ajuster un polynôme de degré m à ces points, c’est-à-dire trouver les coefficients qui permettent au polynôme de passer au plus près de ces points. Si m ≥ n, il existe forcément un polynôme qui soit exactement ajusté à ces données : un tel modèle a assez de capacité pour représenter complètement le jeu de données.
L’optimisation des coefficients du polynôme mène donc à une fonction qui passe exactement par tous les points d’entraînement. Cette situation, alléchante sur le papier, est en fait souvent très fâcheuse. En effet, il faut se souvenir que, comme pour toute procédure de statistique inférentielle, le jeu d’entraînement ne constitue qu’un échantillon de la distribution que l’on cherche à ajuster. À ce titre, les points d’entraînement représentent la distribution mais avec un certain bruit (écart au signal). En utilisant un polynôme de degré élevé, l’ajustement se fera sur ce bruit plutôt que sur la véritable distribution.
Dans la figure 11, les points semblent provenir d’une distribution qui pourrait être ajustée par un polynôme de degré 2 (courbe verte). L’utilisation d’un polynôme de degré 10 (courbe marron) mène à un ajustement plus précis des points d’entraînement, mais nous constatons aisément que la capacité « excédentaire » du modèle a servi à ajuster le bruit. Une telle configuration d’entraînement mène souvent en outre à un modèle ajusté très éloigné de la fonction génératrice dans les plages où il n’y a pas suffisamment de données d’entraînement (figure 4, tout à droite par exemple). Lors d’une phase de prédiction d’une nouvelle donnée, l’ajustement proposé risque de ne pas être satisfaisant. On parle alors de sur-apprentissage : l’algorithme a appris « par cœur » les données d’entraînement sans en tirer la « substantifique moelle » [Rabelais, 1534].
Les réseaux de neurones doivent faire face à cette difficulté. En effet, le nombre de poids d’un réseau est dans de nombreux cas bien supérieur au nombre de paramètres de l’hyperplan permettant de séparer les données d’entrée selon leurs étiquettes. Des méthodes dites de régularisation sont alors implémentées pour combattre ce sur-apprentissage. Dans le cas « jouet » de régression polynomiale, la solution est de choisir un modèle de degré moindre, adapté au degré de la fonction génératrice. Dans le cas des réseaux de neurones, bien que cette idée fasse partie des méta-méthodes pour limiter le sur-apprentissage et soit même la clé de voûte de certaines architectures, nous souhaitons en général conserver la grande capacité de ces réseaux car c’est elle qui permet de générer des caractéristiques variées et sophistiquées. La solution pour obtenir un modèle utile est alors d’augmenter au maximum le nombre de données afin de contraindre la frontière de décision et d’éviter les zones « vides » dans lesquelles les prédictions du modèle risquent d’être aberrantes.
Les algorithmes d’apprentissage profond nécessitent donc pour donner des performances convenables un nombre de données extrêmement important. De plus, il est nécessaire que ces données soient annotées, c’est-à-dire qu’elles aient reçu une étiquette. En fonction de l’application, l’annotation peut être extrêmement chronophage ou coûteuse. Ceci est particulièrement vrai dans des domaines où cette annotation doit être réalisée par des expert·e·s tels que l’agronomie ou la médecine, et/ou pour des tâches plus fines telles que la segmentation.
En agronomie et en médecine, il peut s’agir par exemple de la détection de maladies par imagerie. Pour détourer une lésion, il faut détourer manuellement la région concernée ce qui est très chronophage.
6. Impact sociétal
En tant que nouvelle technologie l’apprentissage profond soulève des questions sur son usage. Elles sont d’ordres diverses. Bien sûr l’usage de cette méthode d’IA peut poser des problèmes éthiques. L’équilibre des bases de données d’apprentissage va conditionner le résultat de l’algorithme. Quand il s’agit de données liées à nos sociétés, il convient donc de veiller à la bonne représentativité de cette société pour éviter des biais (âge, genre, couleur de peau, ...). C’est une question délicate dans la mesure où cette société est elle-même en évolution. Un autre aspect éthique porte sur l’interprétabilité des décisions prises par les algorithmes. Cette décision résulte du passage de l’information dans l’ensemble du réseau dans des espaces de dimension qui dépasse notre entendement et ne s’exprime pas de façon sémantique.
Ceci est particulièrement problématique pour des applications dans le domaine médical ou encore pour des questions de justice qui nécessitent une justification et une incertitude exprimés en des termes compréhensibles par des humains. L’interprétabilité est donc une thématique de recherche très actuelle en IA.
L’usage de l’IA déclenche de nombreux autres débats autour de questions éthiques. L’impact sociétal de l’IA concerne également la question de l’emploi. Certains emplois sont menacés par les performances supra-humaines des algorithmes comme ceux à base d’apprentissage profond. Les partisans technophiles de ces algorithmes indiquent que de nouveaux emplois de "data-scientist" sont créées pour développer justement ces algorithmes.
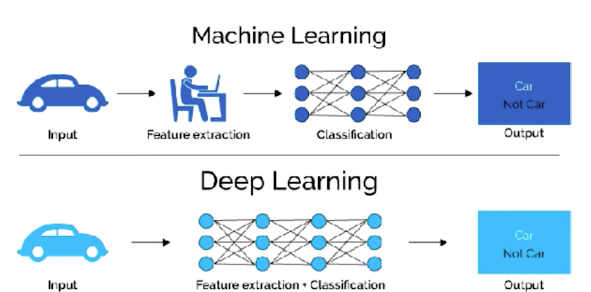
Figure 12. Machine learning versus deep leanring
Un aspect peu discuté est que le niveau de qualification pour développer ces algorithmes n’est pas forcément très élevé. En effet, les codes des algorithmes d’apprentissage profond sont largement disponibles. Le travail du data-scientist consiste donc principalement à annoter les données et à régler les hyperparamètres. Le temps de développement est considérablement réduit par rapport aux approches classiques où l’algorithme était programmé. Une solution logicielle peut ainsi être obtenue en moins d’une semaine là où il fallait plus d’un an au début des années 2000. Certains travaux d’annotation de données sont même réalisés sur des plateformes d’annotation en ligne qui mobilisent des armées de petites mains pour des sommes dérisoires. L’apprentissage non supervisé est donc une thématique de recherche très actuelle en IA.
Un dernier aspect, moins souvent médiatisé, est la consommation énergétique de ces méthodes d’IA. Il est désormais connu que le stockage des données sur les data centers représente une part importante (plus grande que celle de l’aviation civile par exemple) de la contribution de l’activité humain à l’effet de serre. Les méthodes d’apprentissage profond qui sont, comme on l’a expliqué, gourmandes en données sont également de grandes consommatrices d’énergies. Elles nécessitent une parallélisation des étapes de convolution par des composants de type cartes graphiques. La recherche de nouvelles architectures de réseaux de neurones plus éco-responsables est donc une thématique de recherche très actuelle en IA.
7. Ressources complémentaires
Une démonstration de réseaux de neurones en ligne est disponible sur le site Playground.tensorflow.org via une interface très intuitive. On y retrouve tous les éléments présentés dans ce document. Les élèves peuvent voir les réseaux de neurones en action pour une tâche de classification binaire sans avoir à programmer. Un exemple d’utilisation pédagogique de cette interface est proposée sur la vidéo de la chaîne youtube de l’auteur.
L’utilisation des réseaux de neurones amène un certain nombre de questions éthiques abordées dans la vidéo, figure 13.
Pour citer cet article :
Introduction à l’apprentissage profond (deep learning) de l'intelligence artificielle, David Rousseau, Clément Douarre, octobre 2021. CultureSciences Physique - ISSN 2554-876X, https://culturesciencesphysique.ens-lyon.fr/ressource/IA-apprentissage-Rousseau.xml