Aquas diffs

Au lycée comme à l’université, il est classique d’introduire les équations différentielles en invoquant la charge d’un condensateur en électricité, l’oscillation du pendule en mécanique, la décroissance radioactive ou encore la cinétique d’une réaction chimique. Pour motivantes qu’elles soient, ces situations nécessitent un bagage scientifique solide doublé d’un réel sens physique [1, 2, 3, 4]. Plus simple et quotidien, le problème dit de la « vidange » ou de la « purge » d’un récipient conduit naturellement à des modèles souvent du premier ordre et accessibles dès la classe de Terminale [5]. Les contextes d’application sont variés : réservoir sans couvercle type « baignoire » ou avec couvercle type « bidon / cubi / cuve » ; réservoir sous pression type « fusée à eau », « spray aérosol » ou « bonbonne de gaz », ou soumis à une force extérieure type « vessie » ou « bouée dégonflée par constriction ». Mais grosso modo, tout revient à ce seul principe, assez intuitif et que nous tiendrons pour acquis tant que l’orifice de sortie (bonde, valve, soupape, ...) est petit :

Au premier ordre il existe donc une relation entre \(m\) et \(\frac{dm}{dt}\).

Dans cet article, pour une approche mathématique pédagogique, nous négligerons ainsi les phénomènes du deuxième ordre comme la capillarité ou la viscosité.

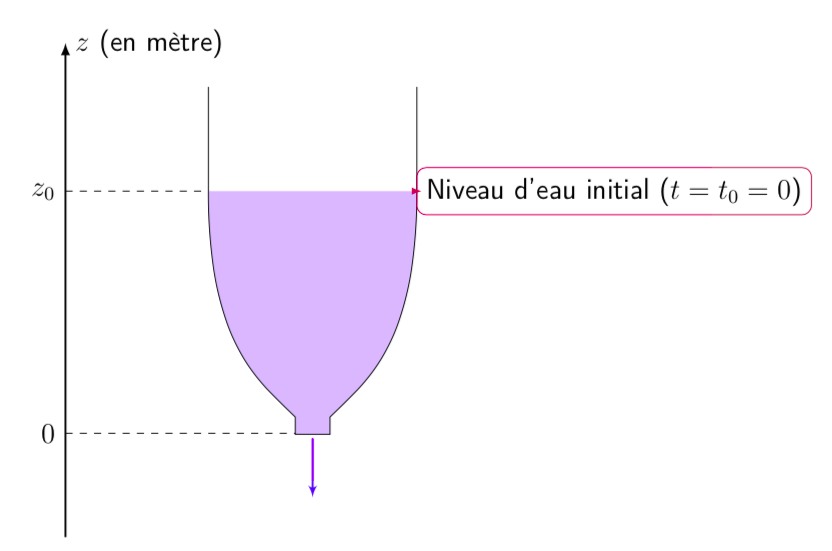
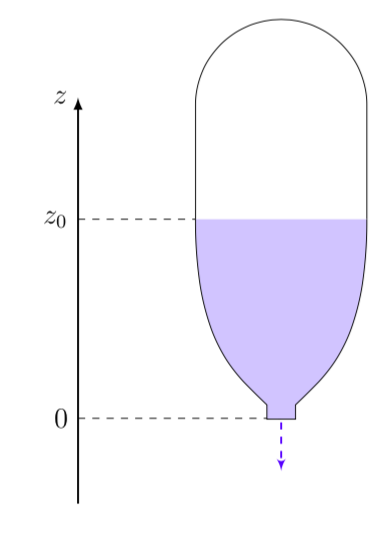
Faisons l’expérience avec une demi-bouteille, assimilée à un cylindre, renversée tête en bas, le fond à l’air libre, figure 1. Remplissons-la jusqu’à la hauteur \(z_0\) et débouchons-la à l’instant \(t = t_0\) (typiquement \(t_0 = 0\)). Notons \(z(t)\) le niveau d’eau restante en fonction du temps, la condition initiale imposant \(z(t_0) = z_0\).

On utilise ici une bouteille, assimilée à un cylindre, dont le culot a été découpé. La bouteille se vide à travers son goulot. On peut convenir que \(t_0 = 0\). Figure 1.  Vidange d’un réservoir ouvert à l’air libre à travers un orifice de sortie

La hauteur \(z(t)\) est proportionnelle à la masse d’eau contenue dans la bouteille à l’instant \(t\). Tel que le phénomène a été décrit dans le principe ci-dessus, plus ce niveau \(z(t)\) est élevé plus il baisse rapidement puisque plus la pression exercée par la colonne d’eau sur le goulot est forte et, par conséquent, plus la fuite est sévère. La vidange se déroule à une vitesse correspondant à la variation du niveau de la surface libre par unité de temps, notée (au choix) \(z'= \dot{z} = \frac{dz}{dt}\) et que l'on peut a priori modéliser, à l'ordre le plus simple et sans considérations physique, comme proportionnelle à \(z\). Si bien que :

\(\frac{dz}{dt} = c z\)     (eq1)

Où \(c < 0 \) est une constante assurant l’homogénéité de l’équation, et négative pour garantir la décroissance de \(z\).

L'équation linéaire (eq1) mène à l'expression :

$$z = z_0 e^{c(t-t_0)}$$

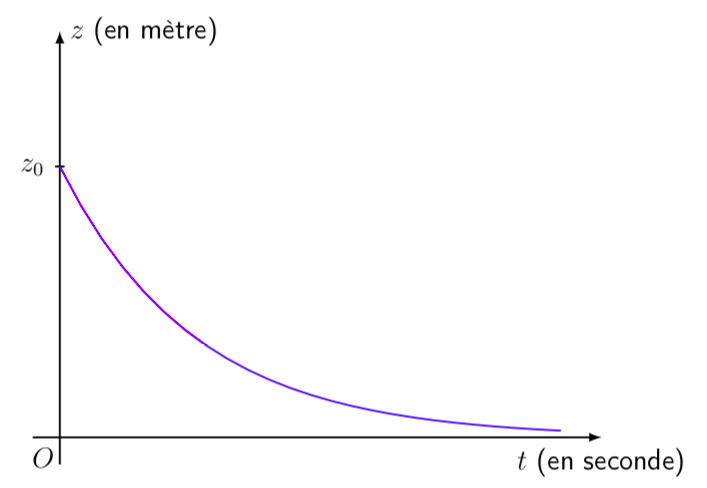
qui tend asymptotiquement vers 0, comme sur la figure 2, ci-dessous. Dès lors, la bouteille se viderait en un temps infini, figure 2.

Figure 2.  Vidange d’un réservoir ouvert à l’air libre (ici une bouteille dont le culot a été découpé) à travers un orifice de sortie (ici le goulot) d’après un modèle mathématique simpliste. Ici, t0 = 0

Notre approche était naïve. En vérité, un modèle plus précis que gouvernent les lois de la physique et notamment le théorème de Bernoulli ^[1] dégage une relation de proportionalité entre \(\frac{dz}{dt}\) d'une part et \(\sqrt{z}\), au lieu de \(z\), d'autre part.

S'ensuit la formule de Torricelli ^[2] :

\(\frac{dz}{dt} = C \sqrt{z}\)    (eq2)

Où \(C\) désigne une constante ^[3] négative et assurant l'homogénéité de l'équation.

Bien que non-linéaire donc apparemment plus complexe, cette équation (eq2) est pourtant plus facile à résoudre car \(\frac{z'}{\sqrt{z}}\) admet comme primitive \(2 \sqrt{z}\). Il vient ainsi

\(2 \sqrt{z} - 2 \sqrt{z_0} = C (t-t_0)\)

Puis :

\(z = (\frac{C}{2} (t-t_0) + \sqrt{z_0})^2\)

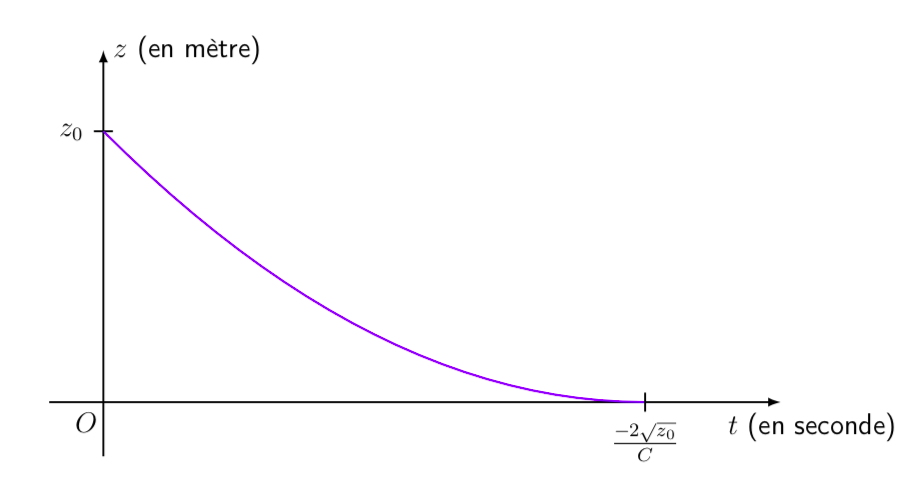
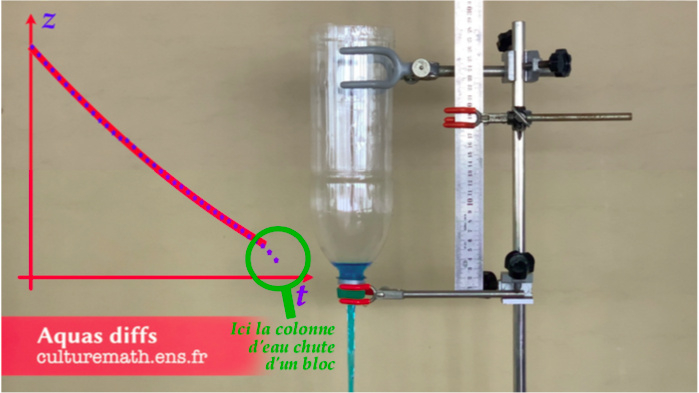
D'où la courbe, sans doute plus crédible puisqu'elle prédit une vidange en un temps fini \(\tau = \frac{-2 \sqrt{z_0}}{C}\), figure 3, que l'expérience réalisée et filmée en laboratoire valide, figures 4 et 5.

Figure 3.  Vidange d’un réservoir ouvert à l’air libre (ici une bouteille dont le culot a été découpé) à travers un petit trou (ici le goulot) d’après un modèle mathématique plus élaboré (modèle de Bernoulli). L’expérience se termine en un temps fini. Ici, t0 = 0

Figure 4.  Vidéo de l'expérience de la vidange d'un réservoir ouvert à l'air libre Allez, on mouille sa chemise ! Expérience réalisée et filmée au laboratoire de sciences physiques du lycée Pierre-Gilles de Gennes – ENCPB à Paris. Les données ont été traitées avec le logiciel de pointage PyMecavideo. On voit très bien la cote \(z\) décroitre paraboliquement, avant de décrocher, précisément quand les diamètres de l’épaulement et du goulot se rejoignent.

Figure 5.  Données de la cote en fonction du temps obtenues à l'aide de la vidéo figure 4

La section de la bouteille (de diamètre 9 cm) est ici bien supérieure à celle du goulot (de diamètre 15 mm). Les observations seraient toutefois différentes si l’orifice de sortie (le goulot, ici) avait été plus large ou la bouteille fuselée. Dans un cas même extrême, le goulot et la bouteille pourraient avoir le même diamètre. Quand le niveau d’eau arrive à hauteur de l’épaulement de la bouteille, le passage se resserre. Les diamètres de la colonne d’eau et du goulot se confondent. Sur la vidéo, nous observons à ce moment que la colonne d'eau chute brutalement,. L'eau tombe d'un bloc, en piqué. Nous ne prenons alors plus en compte les points de mesure suivants. En allant plus loin, on pourrait chercher quelle forme devrait avoir la bouteille pour avoir un débit régulier : c’est le problème de la clepsydre, posé depuis l’Antiquité.

Demandons-nous plutôt ce qu’il advient lorsqu’on renverse la bouteille entière, sans en percer ni découper le fond, comme sur le schéma, figure 6.

Figure 6.  Vidange d’un réservoir fermé (ici une bouteille dont le fond a été conservé) à travers un petit trou (ici le goulot)

Le comportement de la vidange d'un réservoir dépend de la compétition entre les forces de gravité et de tension de surface. Dans l'exemple de la vidéo, le goulot est beaucoup plus grand que la longueur capillaire. Ainsi, l’eau commence par jaillir sous l'action de la gravité. Ce faisant, la poche d’air enfermée dans la partie supérieure voit son volume augmenter et sa pression diminuer jusqu'à ce que la différence de pression entre l'air ambiant et et l'air enfermé dans la bouteille soit suffisant pour compenser la gravité. La poche d'air agit comme un ressort : la diminution de la pression à l'intérieur permet à la pression atmsophérique extérieure de retenir le liquide dans la bouteille. Elle force alors l'admission d'une bulle d'air dans la bouteille qui, en remontant, rétablit la pression atmosphérique dans la bouteille, vidéo figure 7. L'effet est même accentué avec un flacon de collyre. Le bec, très étroit, entrave davantage le mouvement des fluides et met en jeu des forces capillaires qu'on ne peut plus négliger. Il s'instaure alors un goutte à goutte. Voilà pour les aspects qualitatifs. Sans entrer dans les équations, gageons qu'il y aurait ici, en filigrane, du second ordre, peut-être aussi des dérivées partielles...

Le même prodige se répète quand on vide une brique de lait dans son verre. L’écoulement, très saccadé au départ, en verse parfois à côté, figure 8 et vidéo figure 9.

Figure 8.  Verser sans s’éclabousser ! En orientant le goulot vers le bas, l’air se faufile difficilement. L’écoulement se produit par à-coups, à chaque fois qu’une bulle d’air aura pu pénétrer.

Figure 9.  Vidéo de l'expérience de la vidange d'une bouteille de lait goulot vers le bas

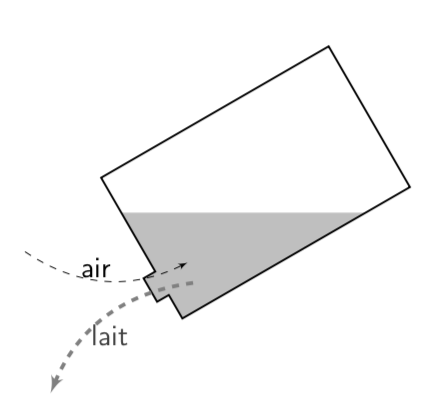
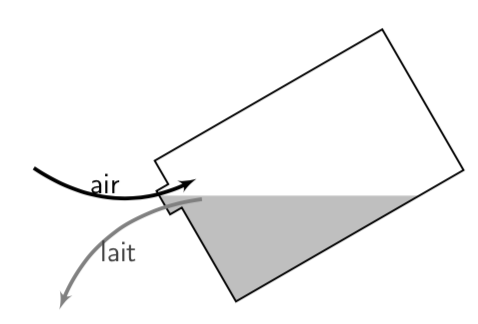
Il y a bien une astuce, contre-intuitive, qui limite ces petits dégâts – et c’est justement pour cette raison que le bouchon est désaxé, figure 10 et vidéo figure 11.

Il faut incliner la brique de l'autre côté.

De la sorte, l’ouverture est d’emblée pour partie dégagée, ce qui aide l’air à pénétrer.

Figure 10.  Verser sans s’éclabousser ! En orientant le goulot vers le haut, l’air peut pénétrer tandis que le lait se déverse. L’écoulement est plus régulier.

Figure 11.  Vidéo de l'expérience de la vidange d'une bouteille de lait goulot vers le haut

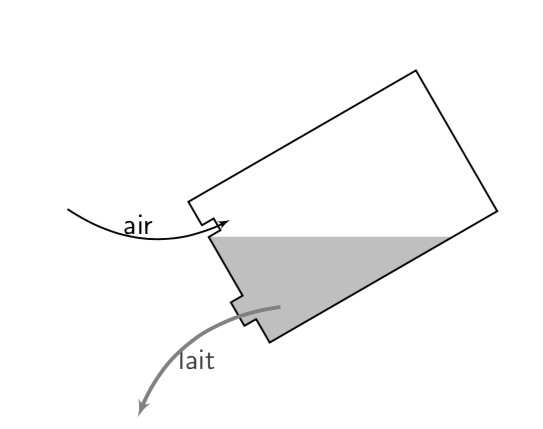
Il existe une astuce encore plus efficace (que ceux qui se sont battus avec un petit suisse connaissent) : percer un simple trou. Non pas à l’arrière – cela fonctionnerait à condition de tout boire d’un coup car l’emballage fuirait – mais sur le dessus, figure 12 et vidéo figure 13.

Figure 12.  Verser sans s’éclabousser ! L’air rentre par le petit trou, en haut à gauche. C’est le principe du flan, dont on décachète l’opercule (située, elle, au dos du moule).

Figure 13.  Vidéo de l'expérience de la vidange d'une bouteille de lait percée d'un petit trou en haut

Gargouillis insolites, bruits de succion, coups de bélier qui hantent votre maison... La plomberie [7] obéit elle aussi aux équations différentielles !

Les auteurs remercient tout particulièrement Cécile Bruyère, inspectrice générale de l’éducation, du sport et de la recherche (groupe physique chimie), Catherine Huet, inspectrice d’académie – inspectrice pédagogique régionale de mathématiques dans l’académie de Versailles, l'équipe éditoriale du site ENS/DGESCO CultureSciences Physique ainsi que Gilles Claudel et Emmanuel Rigolet, inspecteurs d’académie – inspecteurs pédagogiques régionaux de physique chimie dans l’académie de Besançon pour leur relecture très attentive (et bienveillante) du texte.