Activer le mode zen
Ressource au format PDF
Classification
Y'a moyen de moyenner ?
04/04/2022
Résumé
Cet article est co-publié avec le site Culture Math. Dans ce document, nous nous interessons à la façon de réaliser des moyennes en prenant la physique comme domaine d'application.
Table des matières
Introduction - Une moyenne, oui, mais laquelle ?
Il y a bien des façons de moyenner deux nombres : harmoniquement, géométriquement, arithmétiquement (la plus habituelle), quadratiquement — la liste n'est pas exhaustive. Cette variété répond à autant de situations qu'un zeste de Physique a la vertu d'éclairer, jusqu'aux inégalités algébriques (majorations, minorations) qu'elles induisent. Structuré en courts paragraphes largement indépendants, aux modèles volontairement simples associés chacun à une problématique donnée, ce texte est exploitable à loisir dès les classes de collège et de lycée, en cours de mathématiques ou de sciences comme en séances de Travaux Dirigés et de Travaux Pratiques [1] [2] [3] [4].
Comment moyenner deux nombres ?
Rappelons ici les définitions des différentes moyennes. En prenant deux nombres a et b, on peut calculer :
- la moyenne harmonique : \(\frac{2 a \times b}{a+b}\)
- la moyenne arithmétique : \(\frac{a+b}{2}\)
- la moyenne géométrique : \(\sqrt{a \times b}\)
- la moyenne quadratique : \(\sqrt{\frac{a^2+b^2}{2}}\)
1. De la moyenne harmonique et de l'inégalité harmonico-arithmétique
1.1 Vite, une moyenne !
Cinématique et moyenne harmonique
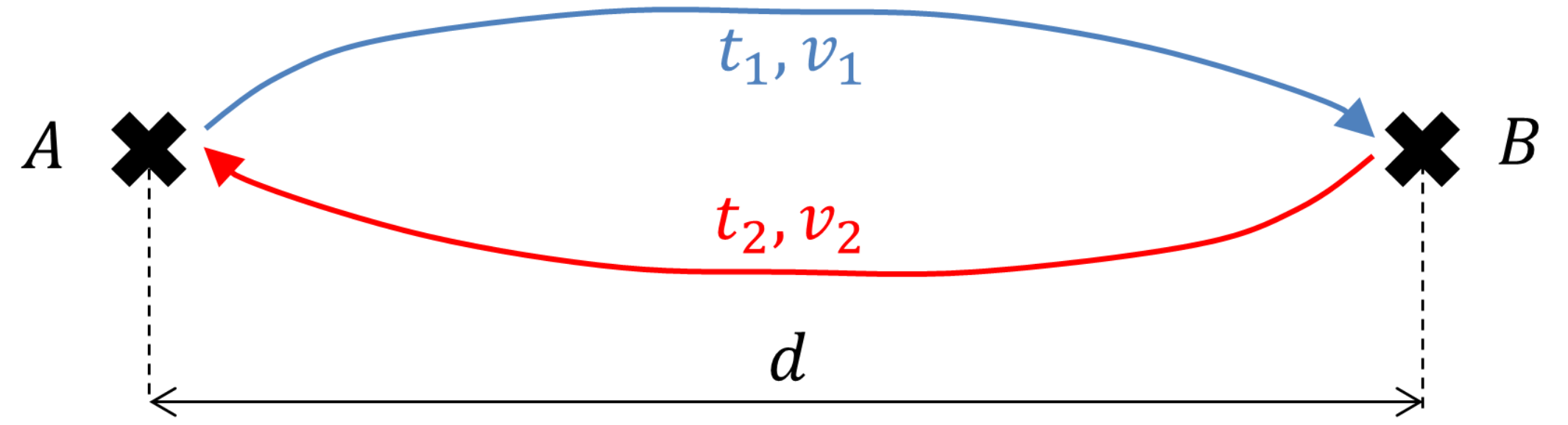
On effectue un voyage aller couvrant une distance \(d\) à la vitesse \(v_1\) pendant un temps \(t_1\) et le voyage retour, sur la même distance \(d\), à la vitesse \(v_2\) pendant un temps \(t_2\), figure 1. On recherche la vitesse moyenne \(\overline{v}\) de l'aller-retour, au sens de la vitesse qui aurait permis d'accomplir la distance équivalente 2\(d\) pendant la même durée totale \(t_1 + t_2\). Pointera alors la notion de moyenne harmonique.
Par définition, le système d'équation noté (eq1) :
$$ \left\{ \begin{aligned} \\ v_1 t_1 \quad &= d \\ v_2 t_2 \quad &= d \\ \overline{v}(t_1+t_2) &= 2d \\ \\ \end{aligned} \\ \right. $$
En extrayant \(t_1\) et \(t_2\) des deux premières équations du système (eq1), on obtient dans la troisième équation :
$$\frac{1}{\overline{v}} = \frac{1}{2}\bigg(\frac{1}{v_1}+\frac{1}{v_2}\bigg) ~~~~\color{gray}{(eq2)}$$
La relation (eq2) indique que l'inverse de la vitesse moyenne est la moyenne usuelle — c'est-à-dire arithmétique — des vitesses inverses. Elle définit ce qu'on nomme une moyenne harmonique, à savoir que :
$$\overline{v} = \frac{2 v_1 v_2}{v_1 + v_2 }~~~~\color{gray}{(eq3)}$$
1.2 Ça résiste… mais plus tant que çela
L'électrocinétique, dont le nom évoque aussi le mouvement (celui des électrons) et, en filigrane, des questions de vitesses ou de durées, mène à des calculs similaires... et même à davantage puisque l'inégalité harmonico-arithmétique y trouvera tout son sens.
Électrocinétique et moyenne harmonique
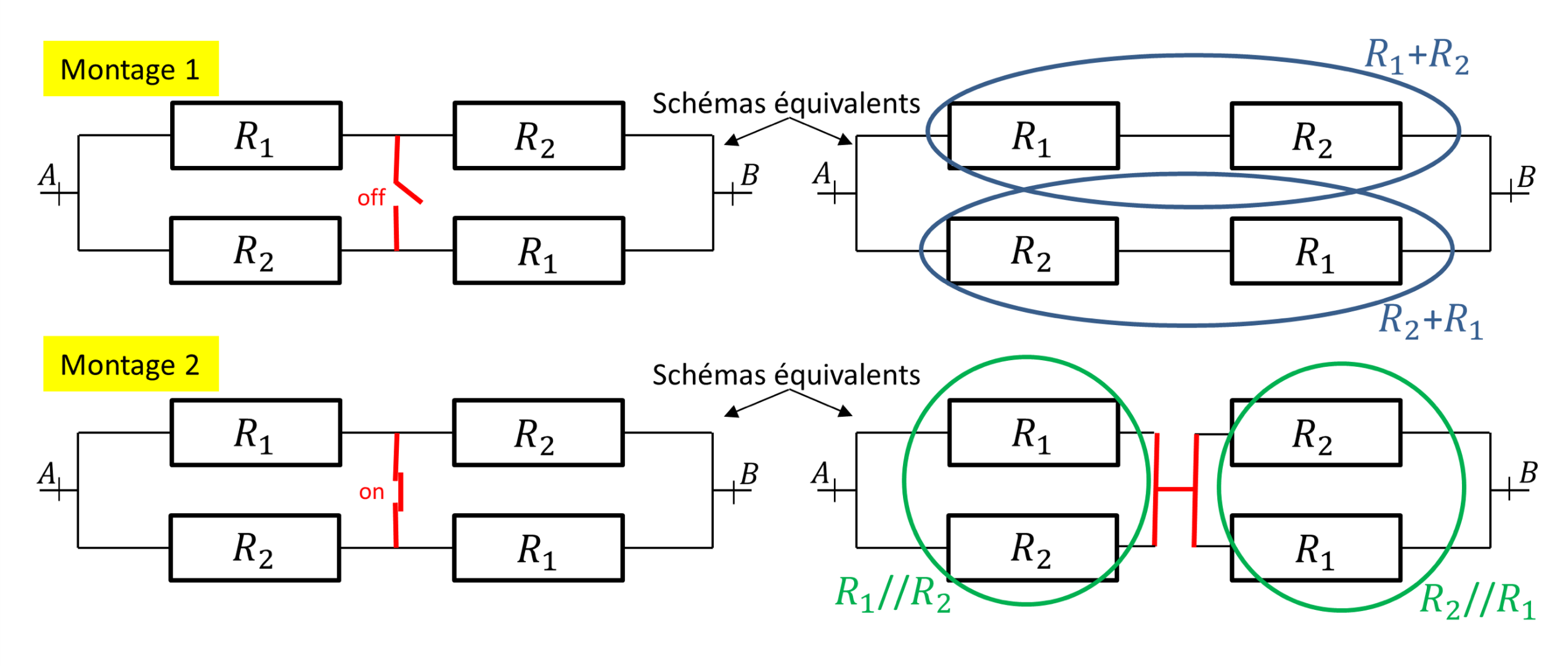
Les montages résistifs de la figure 2 se ressemblent mais dans le premier (en haut), l'interrupteur situé à mi-chemin est ouvert, tandis que dans le second (en bas) il est fermé. On recherche la résistance totale de chacun des montages. L'inégalité harmonico-arithmétique en résultera.
Figure 2. Deux montages résistifs Des résistances totales \(R_{tot,1}\) et \(R_{tot,2}\) de ces montages entre les points \(A\) et \(B\) découlera l'inégalité harmonico-arithmétique. |
Quand l'interrupteur est ouvert, la résistance \(R_{1} + R_2\) est juste en parallèle de la (même) résistance \(R_{1} + R_2\). Ainsi,
$$ R_{\text{tot},1}=\big(R_1+R_2\big)~//~\big(R_2+R_1\big) = \frac{1}{2} \big(R_1+R_2\big)~~~~\color{gray}{(eq4)}$$
C'est une moyenne usuelle.
En refermant l'interrupteur (montage 2), la résistance \(R_1~//~R_2\) est mise en série avec la (même) résistance \(R_2~//~R_1\). Or,
$$ R_1~//~R_2 = \frac{R_1 R_2}{R_2+R_1} = R_2~//~R_1 $$
donc
$$ R_{tot,2} = \big(R_1~//~R_2\big) + \big(R_2~//~R_1\big) = \frac{2 R_1 R_2}{R_1 +R_2}~~~~\color{gray}{(eq5)}$$
C'est une moyenne harmonique. Le second câblage offre au courant une voie supplémentaire à son passage. La résistance totale est donc moindre que dans le premier. D'où naturellement :
$$ \frac{2 R_1 R_2}{R_1 +R_2} ≤ \frac{1}{2}\big(R_1 +R_2\big)~~~~\color{gray}{(eq6)}$$
En clair, la moyenne harmonique de deux nombres positifs est inférieure à leur moyenne arithmétique.
L'expérience réalisée et tournée en laboratoire à l'École Nationale de Chimie Physique Biologie (ENCPB — Lycée Pierre-Gilles de Gennes, Paris) expose le matériel ainsi que les manipulations nécessaires, et valide le résultat sur un exemple, vidéo figure 3.
Il existerait une approche analogue avec, non plus des résistances \(R_1\) et \(R_2\), mais des ressorts aux constantes de raideur \(k_1\) et \(k_2\). Il faut toutefois être vigilant car les formules d'association sont duales : aux ressorts en parallèle, l'addition des constantes ; aux ressorts en série, l'addition de leurs inverses. Comme nous ferons de toutes façons usage de la mécanique un peu plus loin, à la section 2.2, cette branche de la Physique ne sera pas oubliée : patience !
2. De la moyenne géométrique et des inégalités harmonico-géométrico-arithmétique
2.1 Ça ne résiste plus du tout...
Manipuler l'inégalité (eq6) donne :
$$ R_1R_2 \leq \bigg( \frac{R_1+R_2}{2} \bigg)^2 $$
puis, tous les termes en jeu étant positifs, l'inégalité géométrico - arithmétique :
$$ \sqrt{R_1 R_2} \leq \bigg(\frac{R_1+R_2}{2}\bigg)~~~~\color{gray}{(eq7)}$$
Le membre de gauche est ici une moyenne géométrique de deux nombres positifs, laquelle minore leur moyenne arithmétique. Dans la foulée de l'équation (eq7), le produit des moyennes arithmétique et harmonique valant le carré de la moyenne géométrique, on majorerait la moyenne harmonique par la moyenne géométrique. En compilant les informations désormais connues, voici donc un encadrement de la moyenne géométrique par les moyennes harmonique et arithmétique :
$$ \frac{2 R_1 R_2}{R_1 + R_2} ≤ \sqrt{R_1 R_2} ≤ \frac{R_1 +R_2}{2}~~~~\color{gray}{(eq8)}$$
Nous le compléterons ultérieurement. Pour ce faire, changeons d'abord de registre : place à la mécanique !
2.2 Au calcul bien pesé
Tout le monde connaît la balance à plateaux. Ses deux plateaux sont suspendus en chaque extrémité d'un fléau, lequel est retenu, en son milieu, par une attache servant de pivot, figure 4. Quand les plateaux sont identiquement chargés, le fléau demeure à l'horizontale. Sinon, il penche du côté le plus lourd. Mais il arrive que les deux bras soient inégaux et qu'on en ignore leurs longueurs exactes \(d_1\) et \(d_2\). C'est pour éviter que les mesures ne s'en trouvent faussées qu'une méthode dite de double pesée avait été mise au point au XVIIIe siècle.
Figure 4. Une balance à plateaux suspendus Idéalement, \(d_1 = d_2\) et l'équilibre assure l'égalité des masses \(M_1\) et \(M_2\). Dans un cadre plus général, l'équilibre tient à l'égalité des moments qu'exercent les deux masses sur l'instrument par rapport au pivot : \(M_1 \times d_1 = M_2 \times d_2\). |
Mécanique du solide et double pesée
Soit une masse \(M\) à peser. On la place sur le plateau gauche pour l'équilibrer avec une première tare \(m\) à droite. Puis on la place sur le plateau droit pour l'équilibrer avec une seconde tare \(m'\) à gauche. L'inégalité géométrico-harmonique affleurera.
L'équilibre de la première pesée traduit l'équation des moments (aussi dite loi d'Archimède[1])
$$ M d_1 = m d_2~~~~\color{gray}{(eq9)}$$
et celui de la seconde :
$$ m' d_1 = M d_2~~~~\color{gray}{(eq10)}$$
En divisant membre à membre (eq9) et (eq10), les quantités concernées étant toutes non nulles car strictement positives, nous obtenons :
$$ \frac{M}{m'} = \frac{m}{M} $$
donc :
$$ M^2 = mm' $$
puis, en extrayant le radical :
$$ M = \sqrt{mm'}~~~~\color{gray}{(eq11)}$$
Nous reconnaissons en \(M\) la moyenne géométrique de \(m\) et \(m'\). La démarche, filmée à même la paillasse, est présentée en vidéo figure 5.
Figure 5. Mécanique du solide et double pesée |
Allons maintenant jusqu'à interpréter l'inégalité géométrico-arithmétique (eq7) en termes de pesées. Prenons une balance, parfaite celle-ci, aux bras gauche et droit précisément de même longueur \(d_1 + d_2\). Plaçons à gauche \(m + m'\), à droite \(2M\), comme sur la figure 6. La gauche l'emporte. En effet :
$$ \big(m +m'\big)\big(d_1 + d_2\big) - 2 M \big(d_1 + d_2\big) = \big(m+m'\big)\big(d_1 + d_2\big) - 2Md_1 - 2Md_2 $$
$$ \begin{align} \big(m+m'\big)\big(d_1+d_2\big) - 2M \big(d_1 + d_2\big) &= \big(m+m'\big)\big(d_1+d_2\big) -2 m d_2 -2 m' d_1\\ &= m \big(d_1-d_2\big) - m' \big(d_1-d_2\big) \\ &= \big(m-m'\big)\big(d_1-d_2\big)~~~~~~~~\color{gray}{(eq14)} \end{align} $$
Or plus un bras est long, plus la masse à y suspendre est légère. Donc si \(d_1 ≤ d_2\), \(m ≤ M ≤ m'\), les rôles s'inversant quand \(d_2 ≤ d_1\). Par conséquent le produit de l'(eq14) est positif.
3. De la moyenne quadratique et de l'inégalité arithmético-quadratique
Statique des fluides
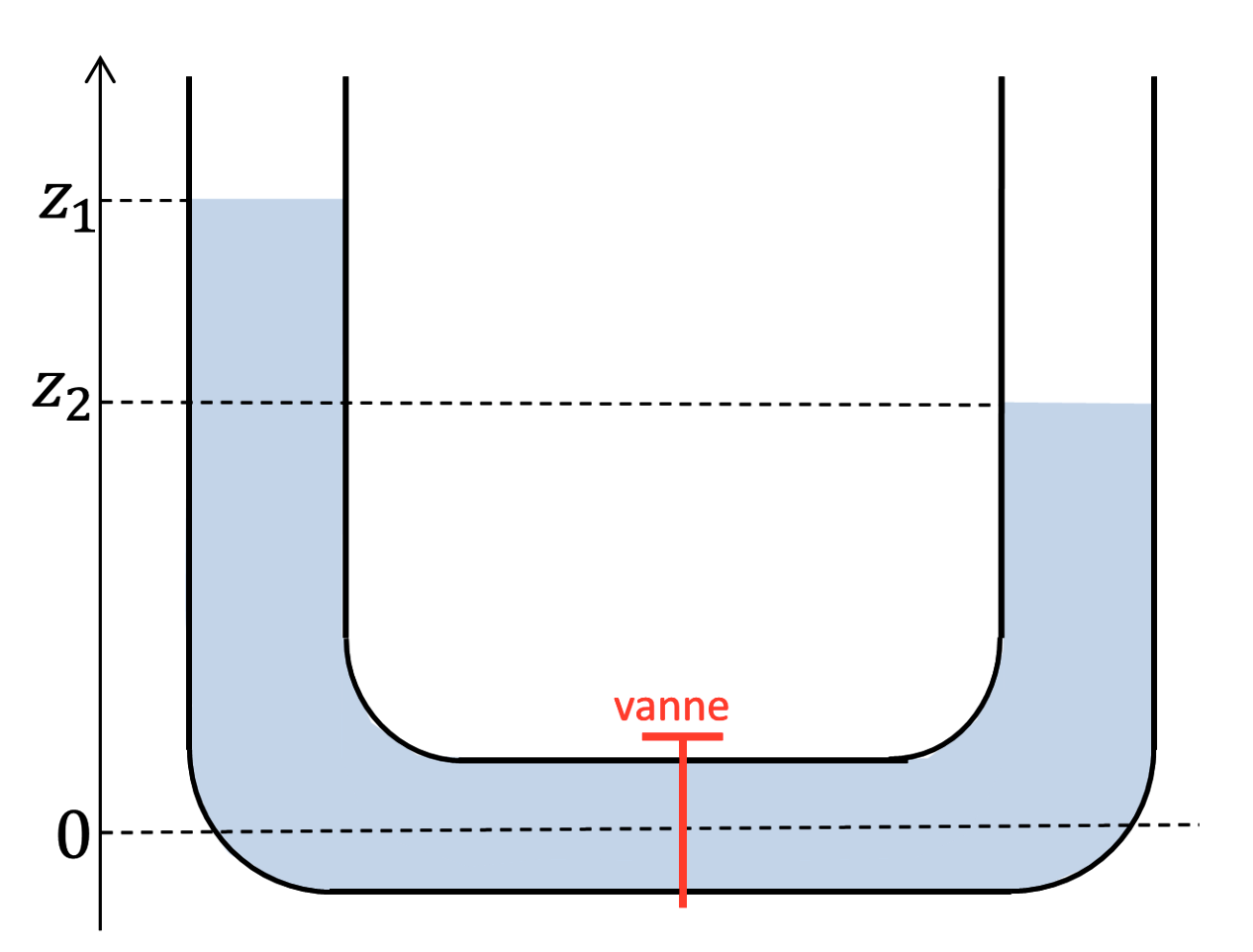
Un tube en U est constitué de deux éprouvettes cylindriques et identiques, posées verticalement et reliées par leur fond (niveau 0 de référence) grâce à un conduit. On déséquilibre le système à l'aide d'une vanne initialement fermée, comme en figure 7, ou bien en jouant sur les pressions appliquées aux deux ouvertures, comme sur le protocole filmé figure 9. Le tube gauche est ainsi rempli d'eau jusqu'à la hauteur \(z_1\), le droit jusqu'à la hauteur \(z_2\). En se ré-équilibrant, soit qu'on aura ouvert la vanne (figure 7), soit qu'on aura décapuchonné à l'air libre les deux orifices (vidéo figure 9), le système retrouve, après quelques mouvements d'oscillation, sa stabilité. Émergera l'inégalité arithmético-quadratique.
Attention - Nous faisons remarquer, dans cet exemple, que les variables \(z_1\) et \(z_2 \) sont liées (les tubes sont de même diamètre). Mais nous les traiterons ici comme deux variables indépendantes.
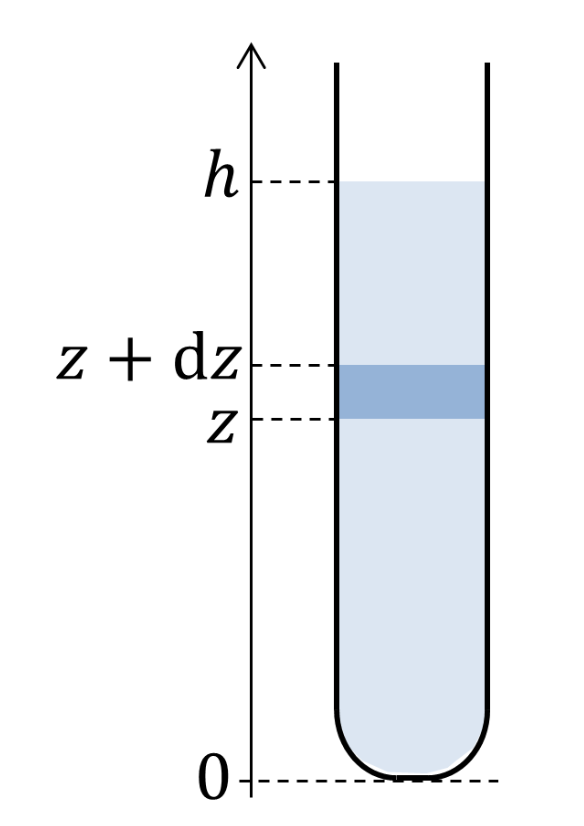
Soit \(S\) la section du tube. Hisser du niveau 0 au niveau \(z\) un disque d'eau d'épaisseur infinitésimale \(dz\) demande le travail :
$$ \text{d}W = \big(\rho S \text{d}z\big) g z $$
où \(\rho\) désigne la masse volumique de l'eau - donc \(\rho S \text{d}z\) la masse du disque d'eau, et \(g \) l'accélération de pesanteur à la surface de la Terre, figure 8. L'énergie potentielle \(E_p\) qu'accumule une colonne d'eau de hauteur \(h\) vaut ainsi
$$ E_p = \rho g S \int_{0}^{h} z \text{d}z = \rho g S \frac{h^2}{2} $$
Ce résultat était tout sauf inattendu : il correspond à l'énergie potentielle du centre de gravité de la colonne d'eau, situé à la hauteur moitié \(\frac{h}{2}\) et concentrant la masse \(\rho S h\). Nous aurions ainsi pu nous affranchir de tout calcul intégral.
Au début de l'expérience, l'eau contenue dans les deux éprouvettes a emmagasiné l'énergie potentielle :
$$ E_p^\text{tot} = \rho g S \frac{z_1^2+z_2^2}{2}~~~~~~~~\color{gray}{(eq15)}$$
En ouvrant la vanne (figure 7) ou les capuchons (vidéo figure 9), le système se met à osciller tout en abandonnant une partie de son énergie par frottement visqueux sur les parois de verre. De l'énergie est dissipée sous forme thermique, le balancement s'amortit, puis le système se stabilise. Les deux éprouvettes affichent enfin le même niveau d'eau, l'un s'étant élevé de ce que l'autre lui aura cédé de liquide. L'énergie potentielle devient :
$$ {E_p^\text{tot}}\,' = 2 \rho g S \frac{1}{2} \Big(\frac{z_1+z_2}{2}\Big)^2~~~~~~~~\color{gray}{(eq16)}$$
L'énergie potentielle du conduit d'eau ne compte pas : elle est (artificiellement) nulle puisqu'à cote nulle, et elle ne varie pas au cours du temps. La perte d'énergie est rendue par l'inégalité \({E_p^\text{tot}}\,' \leq E_p^\text{tot}\) qui, via (eq15) et (eq16), se résume mathématiquement à :
$$\Big(\frac{z_1+z_2}{2}\Big)^2 \leq \frac{z_1^2+z_2^2}{2}$$
puis, les termes en jeu étant positifs, à :
$$\frac{z_1+z_2}{2} \leq \sqrt{\frac{z_1^2+z_2^2}{2}}~~~~~~~~\color{gray}{(eq17)}$$
On reconnaît dans le membre de droite la racine d'une moyenne de carrés, dite moyenne quadratique, laquelle est supérieure à la moyenne usuelle : c'est l'inégalité arithmético-quadratique.
4. Conclusion
Récapitulons en prolongeant l'encadrement (eq8) par l'inégalité (eq17). S'enchaînent alors les inégalités harmonico-géométrico-arithmético-quadratique portant sur tous réels \(R_1\) et \(R_2\) positifs (non simultanément nuls) :
$$\frac{2R_1 R_2}{R_1+R_2} \leq \sqrt{R_1 R_2} \leq \frac{R_1+R_2}{2} \leq \sqrt{\frac{R_1^2+R_2^2}{2}}~~~~~~~~\color{gray}{(eq18)}$$
ou, synthétiquement :
$$H \leq G \leq A \leq Q~~~~~~~~\color{gray}{(eq19)}$$
Les plus curieux se demanderont comment étendre de 2 à \(n\) nombres les définitions de ces moyennes et les inégalités afférentes, en se fondant toujours sur la compréhension de phénomènes physiques ou en imaginant d'autres contextualisations. Et, côté bibliographie, on consultera par exemple avec intérêt [5] [6] [7] [8] [9].
Médiane
Lorsque l'on étudie une série de plusieurs nombres, il peut être aussi pertinent de s'intéresser à la médiane. Cette dernière sépare la moitié des effectifs de la série en deux parties égales. Prenons par exemple un automobiliste effectuant un trajet avec une vitesse de 50 km/h pendant 1 h, puis 130 km/h pendant 2 h. La série s'écrit : 50 130 130. Sa vitesse moyenne peut être calculée à l'aide de la moyenne arithémtique :
$$ v_m = \frac{50 + 130 + 130}{3} \approx 103 \text{ km/h}$$
Sa vitesse médiane sera de 130 km/h.
Si maintenant l'automobiliste roule pendant 100 km à la vitesse de 50 km/h puis pendant 200 km à la vitesse de 130 km/h. La série s'écrit de la même manière : 50 130 130. Sa vitesse médiane sera toujours de 130km/h mais sa vitesse moyenne (moyenne harmonique) sera :
$$ v_m = \frac{100 + 200}{\frac{100}{50}+\frac{200}{130}} \approx 85 \text{ km/h}$$
Dans cet exemple la médiane reste la même. Cet indicateur a « plus de sens » lorsque l'on parle, par exemple de salaire médian de l'ensemble des français plutôt que de salaire moyen.
Références
- [1] Programmes du cycle 4 du collège, Bulletin officiel spécial n°31 du 30 juillet 2020, 2020.
- [2] Programme d'enseignement de mathématiques de la classe de seconde générale et technologique, Bulletin officiel spécial n°1 du 22 janvier 2019, 2019.
- [3] Programme d'enseignement de physique-chimie de la classe de première générale, Bulletin officiel spécial n°1 du 22 janvier 2019, 2019.
- [4] Programme d'enseignement de physique-chimie de la classe de terminale générale, Bulletin officiel spécial n° 8 du 25 juillet 2019, 2019.
- [5] Levi M., A Water-Based Proof of the Cauchy–Schwarz Inequality, The American Mathematical Monthly, 2020.
- [6] Levi M., The mathematical mechanic, Princeton University Press; 2009.
- [7] A Viscosity Proof of the Cauchy–Schwarz Inequality, The American Mathematical Monthly, 2015.
- [8] Padrón M., Plaza Á., A mechanically-based proof of the arithmetic mean harmonic mean inequality, International Journal of Mathematical Education in Science and Technology, 2021.
- [9] Hecht E. Physique. de Boeck; 2013.
Pour citer cet article :
Y'a moyen de moyenner ?, Karim Zayana, Jean-Noël Bernard, Ivan Boyer, avril 2022. CultureSciences Physique - ISSN 2554-876X, https://culturesciencesphysique.ens-lyon.fr/ressource/Moyenne-maths.xml