Activer le mode zen
Ressource au format PDF
Mots-clés
Classification
Intelligence artificielle et jeu de Nim (2/2) - Codage et applications
27/02/2023
Ce travail a été soutenu par l'Agence Nationale de la Recherche dans le cadre du projet ASMODEE - SAPS - RA - MCS 2021.
Résumé
Cet article en deux parties propose un atelier d'informatique débranchée, activité possible à faire en classe, pour introduire l'apprentissage par renforcement. L'atelier, initialement imaginé par Eric Duchêne et Aline Parreau, a été proposé de nombreuses fois à la Maison des Mathématiques et de l'Informatique (Lyon). Dans ce second article on présente les codes pour programmer l'apprentissage par renforcement sur une machine en prenant pour exemple le jeu de Nim et on présente quelques applications dans le domaine de la physique de ce type d'apprentissage machine.
Table des matières
Série de 2 articles sur Intelligence artificielle et jeu de Nim
Article 1/2 prédédent : « l'intelligence artificielle et jeu de Nim (1/2) - Fonctionnement de l'apprentissage par renforcement ».
1. Codage du jeu de Nim
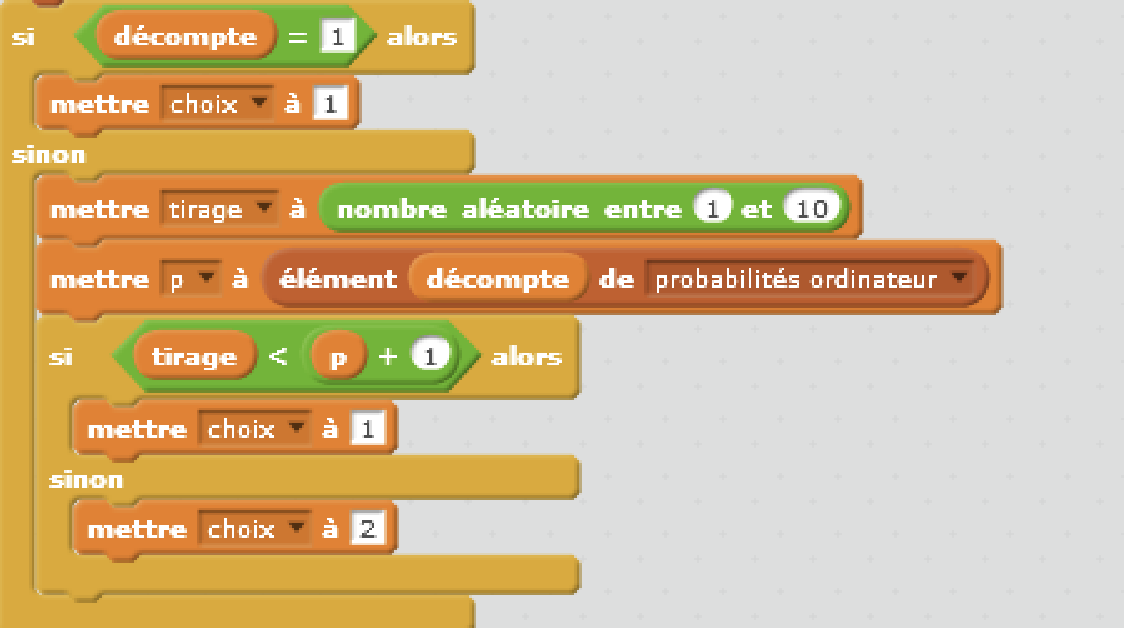
Nous avons vu les principes d'apprentissage machine "avec les mains" dans l'article précédent : « l'intelligence artificielle et jeu de Nim (1/2) - Fonctionnement de l'apprentissage par renforcement ». Il est maintenant intéressant de les programmer avec votre langage de programmation préféré. Vous trouverez les programmes en Scratch [1] et en Python [2] sur le site de la Maison des mathématiques et de l'informatique (MMI).
Programmation du jeu de Nim
Jeu de Nim en langage Scratch proposé par la MMI :
- Accéder au document descriptif avec les explications sur le programme Scratch et des activités à faire avec les élèves.
- Téléchargez le le programme Scratch du jeu de Nim.
Jeu de Nim en langage Python proposé par la MMI :
- Accéder au document descriptif avec les explications sur les programmes python et les activités proposées.
- Téléchargez le le programme Python machine contre humain·e. du jeu de Nim.
- Téléchargez le le programme Python machine contre machine. du jeu de Nim.
Faire programmer aux élèves la stratégie gagnante directement, ou l'apprentissage par renforcement, est tout-à-fait possible et permet de faire le lien entre l'activité et la programmation.
2. D'autres jeux pour aller plus loin
Plusieurs jeux permettent d'illustrer les divers apprentissages abordés dans ces deux articles.
2.1 Le jeu de Choco Chomp
C'est encore un jeu à deux joueur·ses (J1 et J2) à information complète, sans hasard, se terminant en un nombre fini de coups par une victoire de J1 ou J2. Donc J1 ou J2 a une stratégie gagnante. Ce jeu illustre le fait que, parfois, un argument permet de dire qui a la stratégie gagnante, sans toutefois pouvoir l'expliciter comme pour le jeu de Nim.
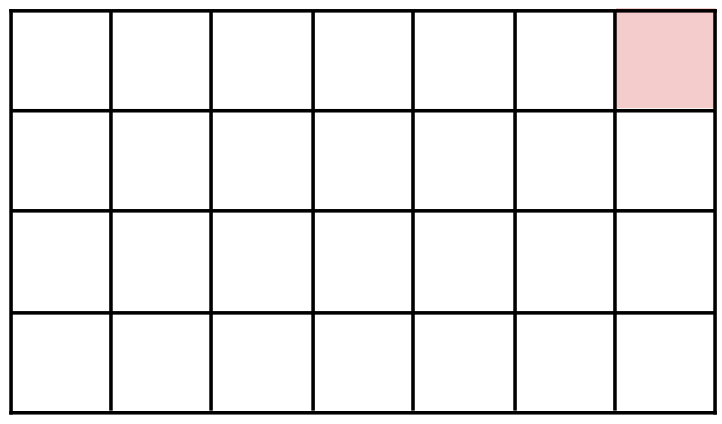
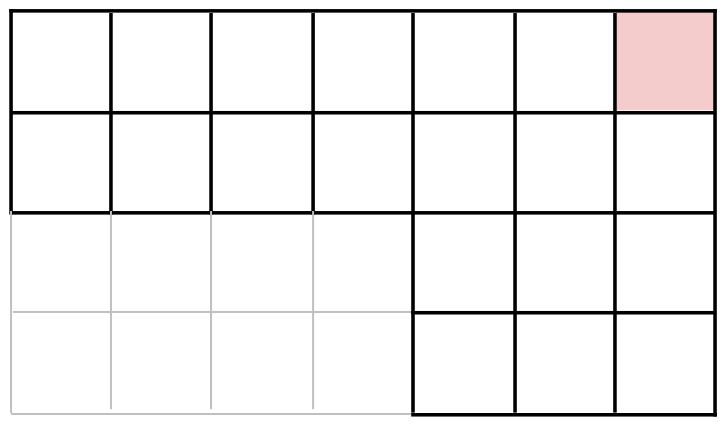
On part d'une tablette de chocolat rectangulaire de quatre par sept, figure 1.
La règle du jeu est la suivante : chacun·e à son tour enlève un morceau de la tablette, celui·celle qui prend le carré rouge (empoisonné), en haut à droite, a perdu.
Figure 1. Initialisation du jeu du Choco Chomp |
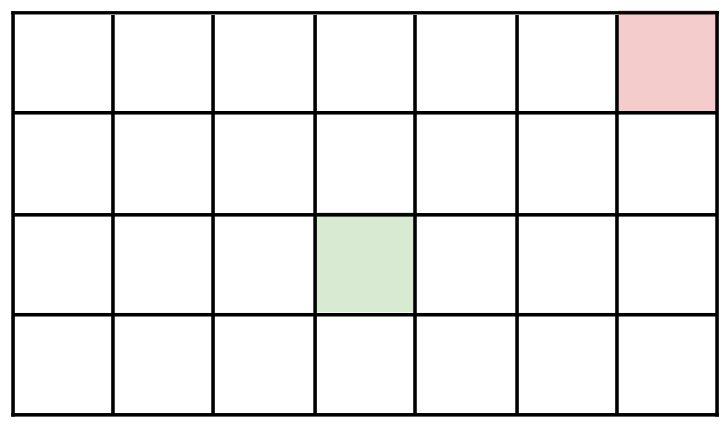
Comment prend-on un morceau de tablette ? On choisit un carré et on enlève tout ce qui se trouve en bas à gauche de ce carré. Voici un exemple de début de partie. J1 choisit ce carré :
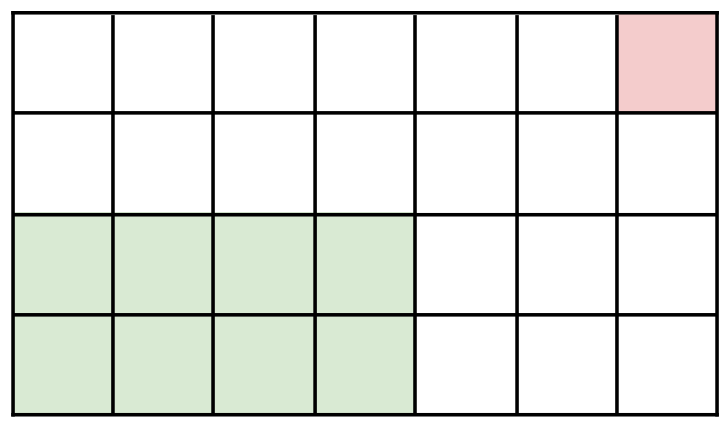
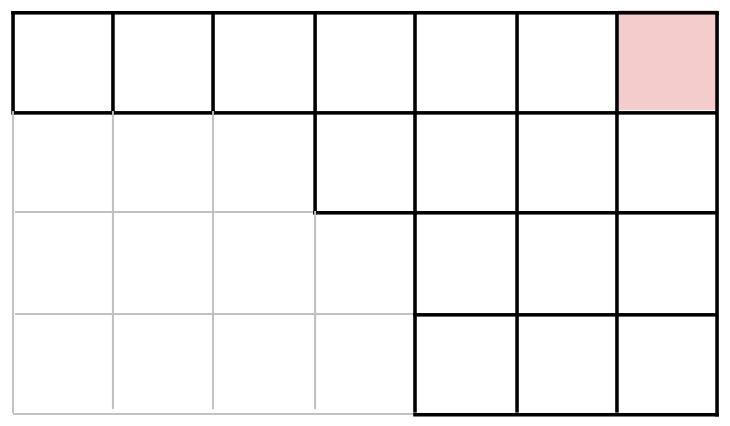
Il enlève donc toute la partie verte, figure 3.
J2 se retrouve donc avec la tablette suivante, figure 4.
Le J2 choisit par exemple le troisième carré en partant de la gauche et deuxième en partant du haut, on arrive alors à la tablette figure 5.
Et ainsi de suite….
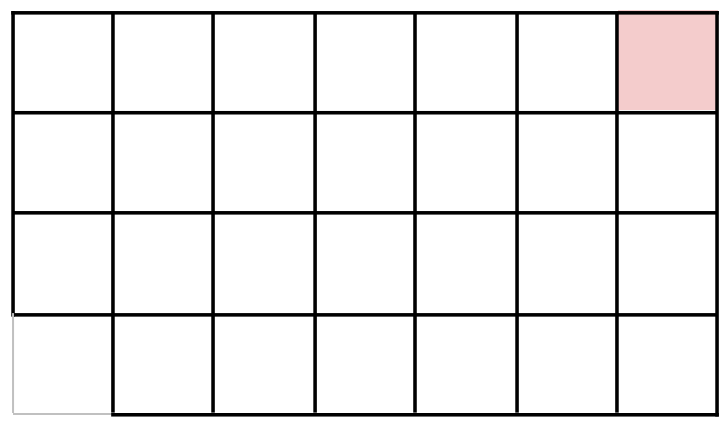
Pour ce jeu, on peut montrer que J1 a nécessairement une stratégie gagnante, sans pour autant être capable de l'expliciter. La preuve repose sur le vol de stratégie. Commençons par imaginer que J1 commence par ne prendre que le coin en bas à gauche, figure 6.
Soit ce coup est gagnant pour J1 (fait partie d'une stratégie gagnante), ce qui signifie que quelque soit le coup de J2, il existe un coup de J1 tel que quelque soit le coup de J2, il existe un coup de J1, etc., tel que, à la fin, J1 gagne. Sinon, c'est qu'il existe un coup de J2 tel que quelque soit le coup de J1, il existe un coup de J2, etc., tel que, à la fin, J2 gagne. Ceci signifie que, dans ce deuxième cas, et à partir de la situation ci-dessus, c'est J2 qui a une stratégie gagnante. Mais dans ce deuxième cas, le premier coup de J2, J1 aurait pu le faire et lui voler sa stratégie gagnante. C'est donc bien J1 qui a une stratégie gagnante. Ce raisonnement fonctionne car le coup "prendre le carré en bas à gauche" est inclus dans tous les autres coups possibles.
Mais cette preuve d'existence est non constructive, elle démontre l'existence d'une stratégie gagnante pour J1 mais ne la donne pas effectivement.
On peut ensuite faire un programme par exploration d'arbre pour avoir la suite de positions gagnantes mais si la tablette de départ devient trop grande, même un ordinateur ne pourra pas le faire.
2.2 Le jeu de Nim à plusieurs étages
Une variante connue du jeu de Nim est la suivante : on part de quatre rangées d'allumettes (avec respectivement une, trois, cinq et sept allumettes). Chacun·e son tour, on retire entre une et trois allumettes d'une seule rangée. Celui·celle qui prend la dernière a perdu.
Ce jeu est appelé le jeu de Marienbad et a été popularisé par le film d'Alain Resnais et d'Alain Robbe-Grillet : L'année dernière à Marienbad (1961).
C'est encore un jeu à deux, à information complète, sans hasard, se terminant en un nombre fini de coups par la victoire d'un·e des deux joueur·ses. Il y a donc une stratégie gagnante pour l'un·e des deux. Mais pour qui ? Et quelle est-elle ? Après avoir cherché, on pourra consulter la référence [3].
2.3 Le jeu du morpion et la MIAM
Le morpion est aussi un jeu à deux à information complète, sans hasard, mais cette fois, il y a une possibilité de match nul. En observant l'arbre de jeu, on peut montrer que les deux joueur·ses ont une stratégie de match nul. En fait, on peut même montrer que J1 peut jouer n'importe où au premier coup et a la possibilité de s'assurer le match nul.
Il est possible de faire une machine purement physique illustrant l'apprentissage par renforcement sur le jeu de morpion. En effet, le·la joueur·se qui commence peut rencontrer, en tenant compte des symétries, 304 positions différentes au cours de la partie, ce qui reste raisonnable.
Donald Michie a construit en 1961 une telle machine en boîtes d'allumettes pour illustrer qu'un pur apprentissage par renforcement pouvait être efficace. Il en existe une à la MMI, à Lyon (figure 7).
Vous pourrez retrouver toutes les informations sur cette machine appelée MIAM (machine intelligente/idiote apprenant le morpion) [4]. Il lui faut quand même jouer environ 120 parties pour devenir très bonne, c'est-à-dire pour assurer le nul à (presque) tous les coups.
3. Pour la culture
En 1997, Deep Blue, d'IBM, bat Garry Kasparov (alors meilleur joueur du monde) aux échecs. Deep Blue était surtout une force de calcul brut. Avec 30 processeurs en parallèle, il était capable d'explorer 30 milliards de positions par coup, ce qui lui permettait d'aller jusqu'à une profondeur de 14 coups. Il possédait une bibliothèque d'ouvertures de 4 000 positions environ, avait précalculé toutes les finales à 5 pièces et un certain nombre à 6. De plus, il pouvait piocher dans une immense base de données de 700 000 parties de grands maîtres.
Ce succès de Deep Blue a renforcé la croyance communément admise à l'époque selon laquelle les programmes de jeu progresseraient essentiellement grâce à des avancées techniques, au niveau du matériel. C'est finalement autant un exploit technologique que scientifique puisque l'algorithme utilisé par Deep Bue était de facture assez classique.
Deep Blue explore l'arbre de jeu. Cependant, comme il est impossible d'aller au bout de l'arbre (le nombre de parties possibles aux échecs étant d'environ 10120), il faut utiliser une fonction d'évaluation. Celle-ci permet d'évaluer (donner une note) les chances de gagner des blancs et des noirs étant donnée une position de jeu. Celle utilisée par Deep Blue reposait sur 8 000 critères et était construite à partir du savoir humain. Tout repose ensuite sur une méthode de min-max. Imaginons que DeepBlue joue les blancs et que c'est à son tour. Il regarde un de ses coups possibles et regarde ensuite tous les coups noirs possibles puis il évalue la position. En imaginant que son adversaire va jouer au mieux, donc va essayer de rendre l'évaluation pour les blancs minimale suite à son coup, Deep Blue attribue cette valeur à son propre coup. Il maximise alors sur tous ses coups possibles. Bref, il cherche à maximiser parmi ses propres coups le minimum de la fonction d'évaluation parmi tous les coups suivants de son adversaire. Bien entendu, Deep Blue pouvait faire la même chose avec plus de profondeur (en faisant un max de min de max de min de …) et avait des techniques d'élagage de l'arbre pour éviter d'explorer les branches peu prometteuses. C'est aussi ce que fait un·e humain·e : je ne vais pas sacrifier ma dame si je n'y vois pas un avantage rapide. Cette technique d'exploration d'arbre avec fonction d'évaluation était déjà utilisée dans les années 1950 par A. Samuel dans son programme de jeu de dames. C'était poussé à l'extrême par Deep Blue, grâce à un mélange d'améliorations d'ordre scientifique et d'ordre technologique.
En 2016, AlphaGo, de DeepMind, bat Lee Sedol, considéré comme un des meilleurs joueurs au monde, au jeu de Go. C'est un programme basé sur l'apprentissage par renforcement. Il était communément admis que cela finirait par arriver (une machine meilleure que l'humain·e au Go) mais c'est arrivé plus vite qu'on ne le pensait. Et surtout, la technique utilisée est complètement différente. Bien entendu, la mise en oeuvre de cet apprentissage par renforcement est un peu plus compliquée et subtile que dans l'activité ci-dessus mais cette dernière permet d'en saisir le principe.
4. Applications de l'apprentissage par renforcement
Pour finir, nous pouvons nous intéresser à quelques applications de l'apprentissage par renforcement dans des domaines qui touchent à la physique ou l'ingénierie.
4.1 Trafic et véhicule autonome
La conduite autonome est une application prometteuse de l'apprentissage par renforcement. Le véhicule n'a pas à connaître le code de la route, il suffit pour l'ordinateur d'apprendre de ses erreurs. Un conducteur intervient lorsqu'une erreur est commise, chaque intervention est une punition comme nous l'avons vu dans le cas du jeu de Nim. L'algorithme est récompensé lorsque qu'il effectue un trajet sans intervention. Pour plus de détails et une application avec un simulateur de voiture on pourra consulter la vidéo d'une équipe de l'Inria travaillant sur un algorithme de conduite de bout-en-bout [5].
L'entreprise Wayve (basée à Londres) montre in-situ l'apprentissage d'un véhicule autonome, dans la vidéo accessible par la figure 8. On peut voir un premier exemple d'apprentissage par renforcement d'une voiture qui ne connait pas le code de la route et n'a pas accès à une carte. La voiture apprend à rester sur la route à l'aide des interventions (punitions) de l'opérateur présent dans l'habitacle [6].
Figure 8. Apprentissage par renforcement pour la conduite autonome, expérience menée par l'entreprise Wayve Source : Wayve [6] |
L'optimisation du trafic routier, par le biais du contrôle des feux tricolores du réseau routier, peut aussi récemment bénéficier des algorithmes d'apprentissage par renforcement [7]. Ici, la problématique est de rendre le trafic routier le plus fluide, c'est-à dire laisser passer le plus de véhicules possibles, sans gêner la sécurité, lors d'une intersection. L'apprentissage par renforcement permet de résoudre ce problème de maximisation.
4.2 Saisie automatique d'objets
Les méthodes d'apprentissage par renforcement sont aussi utilisées dans l'industrie pour améliorer la préhension ou le mouvement des robots [8].
La plupart des problèmes de manipulation d'objets ne peuvent pas être modélisés avec assez de précision. Il est particulièrement compliqué de résoudre, par exemple, un problème comme la réorientation d'objets. L'entreprise Open AI entraîne, à l'aide de simulations, une main robotisée à manipuler des objets [9]. La machine apprend à l'aide d'un algorithme par renforcement. Une fois bien entraînée et à l'aide d'autres algorithmes d'intelligence articficielle, la situation est transposée au monde réel. On peut voir dans la vidéo accessible par la figure 9, les résultats obtenus pour une main faisant pivoter un cube afin de montrer la bonne face par rapport à la consigne donnée.
Figure 9. Apprentissage par renforcement pour la dextérité d'une main robotique, Open AI Source : Open AI [9] |
4.3 Réduction de la consommation énergétique
Dans le domaine énergétique, les méthodes d'apprentissage par renforcement peuvent aussi aider à optimiser l'efficacité des installations.
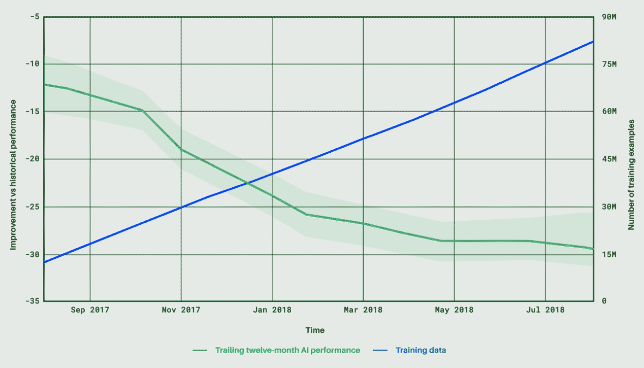
Par exemple, DeepMind (dont on a déjà parlé avec AlphaGo) travaille pour limiter la consommation énergétique des data center utilisés par Google [10][11]. L'objectif est ici de minimiser la dépense énergétique nécessaire au refroidissement des serveurs, tout en gardant les contraintes de sécurité sur les appareils.
Dans son billet [11], Deep Mind annonce une économie d'énergie de l'ordre de 30% depuis la mise en place de la gestion par AI.
Source : DeepMind [11] |
4.4 Conclusion
Nous venons de donner quelques exemples d'applications utilisant l'apprentissage par renforcement. Le champ des possibles est évidemment beaucoup plus large : finance, moteurs de recommandation sur les sites web ou réseaux sociaux, jeux vidéos, médecine…
Références
[1] Programmation du Jeu de Nim en scratch, MMI.
[2] Programmation du Jeu de Nim en python, MMI.
[3] Jeu de Marienbad, Wikipedia.
[4] MIAM, machine intelligente apprenant le morpion, MMI.
[6] Learning to drive in a day, Wayve, You Tube, consulté en janvier 2023.
[7] Création de systèmes de contrôle de feux à l’aide de méthodes d’apprentissage par renforcement, Thèse de M. Treca, 2022.
[8] Apprentissage par renforcement : une IA puissante dans toujours plus de domaines, Hello Future, consulté en janvier 2023.
[9] Learning dexterity, Open AI, consulté en janvier 2023.
[10] Reinforcement Learning : qu’est-ce que l’apprentissage par renforcement ?, Le big data, consulté en janvier 2023.
[11] Saving energy at Google scale, DeepMind, consulté en janvier 2023.
Pour citer cet article :
Intelligence artificielle et jeu de Nim (2/2) - Codage et applications, Olivier Druet, février 2023. CultureSciences Physique - ISSN 2554-876X, https://culturesciencesphysique.ens-lyon.fr/ressource/IA-Nim-2.xml