Activer le mode zen
Ressource au format PDF
Classification
Intelligence artificielle et jeu de Nim (1/2) - Fonctionnement de l'apprentissage par renforcement
20/02/2023
Ce travail a été soutenu par l'Agence Nationale de la Recherche dans le cadre du projet ASMODEE - SAPS - RA - MCS 2021.
Résumé
Cet article en deux parties propose un atelier d'informatique débranchée, activité possible à faire en classe, pour introduire l'apprentissage par renforcement. L'atelier, initialement imaginé par Eric Duchêne et Aline Parreau, a été proposé de nombreuses fois à la Maison des Mathématiques et de l'Informatique (Lyon). Dans ce premier article on s'attache à expliquer "en débranché" le fonctionnement de l'apprentissage par renforcement.
Table des matières
Introduction
L'intelligence artificielle contemporaine et ses succès récents (depuis 2000-2010) reposent en grande partie sur l'apprentissage machine. Celui-ci est utile lorsqu'on ne sait pas comment décomposer une tâche compliquée en sous-tâches simples. La programmation classique consiste à donner une suite d'instructions simples permettant d'arriver au but recherché. Parfois, nous sommes dans l'incapacité de le faire, soit tout simplement parce que nous, humain·es, ne savons pas comment faire, soit parce que nous savons parfaitement effectuer la tâche mais sommes incapables de la décomposer en éléments simples. Dans ce cas, une piste est d'utiliser de l'apprentissage. Cela reste de la programmation. Simplement, on explique comment apprendre à arriver au but sans expliquer directement comment y arriver.
On peut distinguer trois grands types d'apprentissage aujourd'hui : l'apprentissage supervisé (utilisé par exemple pour la reconnaissance d'images), l'apprentissage non supervisé (utilisé par exemple dans les systèmes de recommandation) et l'apprentissage par renforcement (utilisé dans les prises de décision). Dans la plupart des applications, les trois sont mélangés.
Dans la suite, nous proposons une activité permettant d'éclaircir ce concept d'apprentissage en se concentrant sur l'apprentissage par renforcement.
1. Les jeux et l'intelligence artificielle, une longue histoire
Dès les débuts de l'intelligence artificielle, les chercheur·ses se sont intéressé·es aux jeux. Passons en revue quelques grandes dates.
Dès les années 1950, Arthur Samuel (figure 1), travaillant chez IBM, élabore un programme de jeu de dames (dans sa version anglaise, sans mouvement long de la dame) et l'améliorera jusqu'au début des années 1960. C'est en 1959 qu'il introduit un peu d'apprentissage par renforcement dans son programme et c'est à ce moment-là qu'apparaît le terme d'apprentissage automatique (machine learning). Le jeu de dames anglaises a beaucoup plus tard été faiblement résolu par Schaeffer en 2007 : il y a toujours une stratégie de match nul (pour les deux joueur·ses) et Schaeffer construit un programme qui assure le nul contre un·e joueur·se jouant parfaitement mais qui n'est pas forcément capable de gagner contre un·e joueur·se faisant des erreurs (le programme ne transformera jamais une situation de nul en défaite mais peut transformer une position pouvant mener à la victoire en nul - c'est le sens de faiblement résolu).
Entre-temps, on peut noter en 1997 la victoire de Deep Blue, logiciel d'IBM, contre Garry Kasparov, alors champion du monde des échecs (figure 2). Mais, aux échecs, on ne sait toujours pas si les blancs ont une stratégie de victoire (c'est-à-dire s'ils sont absolument certains de gagner en jouant optimalement), on sait juste faire des programmes bien meilleurs que les humain·es.
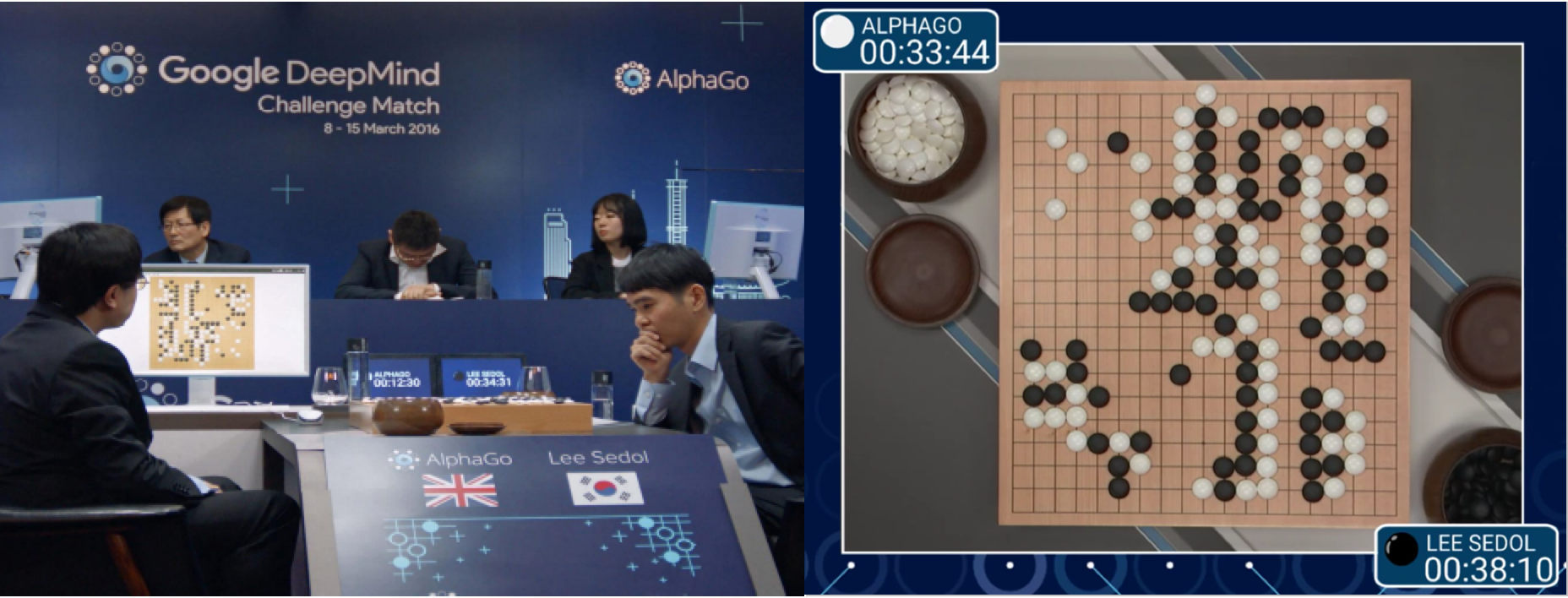
En 2016, AlphaGo défraie la chronique en battant l'un des meilleurs joueurs du monde au Go (figure 3). Si la victoire de la machine ne surprend pas les spécialistes qui savaient que cela finirait par arriver, c'est la rapidité à laquelle cela est arrivé qui a étonné. Un excellent documentaire existe sur cet événement [1].
Figure 3. 2016 : L'IA AlphaGo bat Lee Sedol au Go |
Et aujourd'hui, l'intelligence artificielle s'attaque au poker, aux jeux vidéos, …
2. Fabriquer une machine qui apprend à jouer au jeu de Nim
Nous décrivons ici une activité à mener en classe. On pourra aussi consulter le déroulé de l'atelier tel qu'il est proposé à la MMI [3].
2.1 Le jeu de Nim - règles du jeu
Le jeu de Nim, ou jeu des allumettes, se joue à deux joueur·ses. On dispose un certain nombre d'allumettes, ici huit, sur la table. Chaque joueur·se, chacun·e son tour, a le droit de prendre une ou deux allumettes. Celui·celle qui prend la dernière a gagné. L'idéal est de commencer l'activité en faisant jouer les élèves quelques parties pour qu'iels se familiarisent avec le jeu. Iels devraient repérer quelques éléments de stratégie, comme le fait qu'on a perdu lorsqu'il ne reste que trois allumettes et que c'est à son tour de jouer[1].
2.2 Construction de la machine - matériel nécessaire
Vous aurez besoin, pour chaque machine, de :
- huit verres en carton ou plastique numérotés de 1 à 8
- huit petits gobelets ou récipients
- des billes de couleur (jaune et rouge ici)
- huit allumettes pour jouer contre la machine
- deux verres de réserve de billes.
2.3 Installation de la machine
Il faut placer les huit verres numérotés de 1 à 8 avec les huit allumettes en vis-à-vis ainsi qu'un petit récipient devant chaque verre. Dans les verres 2 à 7, il faut placer deux billes de chaque couleur (jaune et rouge pour nous). Dans le verre 1, il faut mettre seulement deux billes jaunes.
Pour accompagner la description donnée ici et voir une partie de jeu de Nim contre une machine, on pourra regarder la vidéo ci-dessous [2].
Il y a donc trois rôles ici : un·e joueur·se humain·e, la machine et un·e opérateur·trice qui effectue le tirage aléatoire des billes pour la machine (l'opérateur·trice amène l'énergie mécanique à cette machine puisqu'il n'y a pas d'électricité).
2.4 Comment la machine joue-t-elle ?
La machine va commencer [2]. Comme il y a au départ huit allumettes, on va tirer dans le verre 8, une bille de couleur au hasard. On la pose dans le petit récipient à côté du verre 8. Si cette bille est jaune, la machine enlève une allumette ; si elle est rouge, elle enlève deux allumettes. Ensuite, c'est au tour de l'humain·e qui enlève une ou deux allumettes. Quand c'est au tour de la machine, on pioche au hasard une bille dans le verre correspondant au nombre d'allumettes restantes dans la partie.
C'est pourquoi on ne met que des billes jaunes dans le verre 1 : quand il ne reste plus qu'une allumette, la machine ne peut pas en prendre deux.
La machine gagne si elle empoche la dernière allumette, elle perd si c'est l'humain·e qui prend la dernière allumette.
La machine joue au hasard. Pas très efficace… mais à la fin de la partie vient le processus d'apprentissage.
2.5 Comment la machine apprend-elle ?
À la fin de la partie, si la machine a perdu, on va simplement ne pas remettre les billes jouées (stockées dans les récipients) dans les verres dont elles proviennent. On les remet dans la réserve. C'est une punition (terme consacré en apprentissage machine). Cela correspond à un mauvais choix dans la base des possibilités de jeu. Si la machine a gagné, on va remettre ces billes dans les verres en en ajoutant une (prise de la réserve) de la même couleur. C'est une récompense. Par exemple, si la machine a joué rouge au premier coup et qu'elle a gagné la partie, on va remettre la bille rouge plus une autre issue de la réserve dans le verre 8. On fait de même avec tous les verres dans lesquels la machine a pioché au cours de la partie.
En effet, l'idée de l'apprentissage est la suivante : si la machine a perdu, la succession de coups qu'elle a joués a eu une issue malheureuse[3] et on a envie qu'elle les refasse moins souvent. C'est pourquoi on ne remet pas les billes dans les verres, afin de diminuer les probabilités de rejouer ces coups. Par contre, si elle a gagné, cette succession de coups a une issue heureuse et on souhaite qu'elle les rejoue plus souvent, c'est pourquoi on augmente les probabilités qu'elle rejoue ces coups en ajoutant une bille de la couleur jouée dans le verre. Toute l'essence de l'apprentissage par renforcement se trouve dans cette activité.
Dans cette machine, l'opérateur·rice joue une fonction tirage au sort implémentable en programmation, les petits gobelets retournés servent à stocker en mémoire les coups joués pendant la partie, les grands verres contenant les billes stockent en mémoire les probabilités de jouer une ou deux allumettes au cours de l'apprentissage.
On peut faire jouer quelques parties à la machine contre des humain·es. On verra qu'elle perd de moins en moins souvent et qu'elle devient relativement bonne au bout de dix à quinze parties, excellente au bout de vingt. Afin d'éviter le souci de machines qui n'auraient pas appris au bout de 10-15 parties, on peut mettre en commun toutes les machines à la fin pour discussion.
Remarque : au bout de quelques parties, il se peut qu'un verre se vide. Dans ce cas, on le réinitialise en remettant deux billes de chaque couleur dedans.
Nous discuterons plus précisément des avantages et inconvénients de cette technique d'apprentissage dans la section suivante.
3. Analyse de l'activité
3.1 Stratégie gagnante
Tout d'abord, analysons le jeu. Ce jeu est un jeu à deux, à information complète (on connaît à tout moment les coups possibles présents et futurs des deux joueur·ses), sans hasard, se terminant en un nombre fini de coups (chaque coup présentant lui-même un nombre fini de possibilités), avec victoire d'un·e des deux joueur·ses à la fin (il n'y pas de partie nulle). Pour un tel jeu, un·e des deux joueur·ses (que nous appellerons maintenant J1 et J2) a une stratégie gagnante, c'est-à-dire qu'iel peut jouer une série de coups (dépendant de ceux de son adversaire) qui, quoique fasse son adversaire, le·la mènera à la victoire.
En effet, soit J1 a une stratégie gagnante, ce qui signifie qu'il existe un coup pour J1 tel que, quoique fasse J2, il existe un coup pour J1 tel que, etc. à la fin, J1 gagne. Si ce n'est pas le cas, cela signifie que quel que soit le premier coup de J1, J2 a un coup pour contrer, c'est-à-dire un coup tel que quoique fasse J1, il existe un coup tel que, etc., à la fin J2 gagne. En d'autres termes, si J1 n'a pas de stratégie gagnante, c'est que J2 en a une.
Dans le cas du jeu des allumettes avec les règles ci-dessus, la stratégie gagnante n'est pas difficile à trouver et à expliciter. Il suffit de laisser toujours un multiple de trois allumettes à son adversaire. En effet, si on laisse 3n allumettes à son adversaire, il en restera après son coup 3n-1 (s'iel en retire une) ou 3n-2 (s'iel en retire deux). On peut alors se débrouiller pour lui en laisser 3n-3 (autre multiple de 3) en en retirant deux dans le premier cas, une dans le second. Ainsi, on peut s'assurer de toujours laisser un multiple de trois allumettes à son adversaire. Quand il ne lui en reste plus que trois, iel nous en laissera une ou deux après son coup et on pourra prendre la dernière.
Si on démarre avec huit allumettes, c'est donc J1 qui a une stratégie gagnante. C'est d'ailleurs la raison pour laquelle faire jouer la machine en deuxième est risqué : si l'adversaire commence et joue bien, iel gagnera à tous les coups et la machine ne fera qu'être punie.
Ouverture / questions : déterminer quel·le joueur·se a la stratégie gagnante en fonction du nombre d'allumettes de départ ; que se passe-t-il si on peut maintenant retirer une, deux ou trois allumettes ?
3.2 Programmation standard
Comme on connaît la stratégie gagnante pour ce jeu, il serait extrêmement efficace de programmer notre machine directement pour qu'elle gagne dès que possible. Il suffirait de ne mettre dans les verres :
- numéro 1 : que des billes jaunes
- numéro 2 : que des billes rouges
- numéro 3 : un mélange de rouges et de jaunes (peu importe ce qu'elle joue, la machine est dans une situation perdante)
- numéro 4 : que des billes jaunes
- numéro 5 : que des billes rouges
- numéro 6 : un mélange de rouges et de jaunes (peu importe ce qu'elle joue, la machine est dans une situation perdante)
- numéro 7 : que des billes jaunes
- numéro 8 : que des billes rouges
C'est l'implémentation débranchée d'un algorithme donnant la stratégie gagnante. Bien entendu, quand l'humain·e connaît la stratégie gagnante et est capable de la décrire et de la décomposer en étapes élémentaires (comme c'est le cas ici), c'est le plus efficace pour construire une machine/un programme qui gagne : c'est de la programmation classique.
3.3 Exploration d'arbre
Parfois, nous ne sommes pas capables de décrire la stratégie gagnante (même si nous savons qu'elle existe, voir le jeu de ChocoChomp qui sera décrit dans l'article suivant, pour un tel exemple de jeu). Dans ce cas, on peut demander au programme de parcourir tout l'arbre de jeu. Voyons comment cela fonctionne sur le jeu de Nim dans la version proposée.
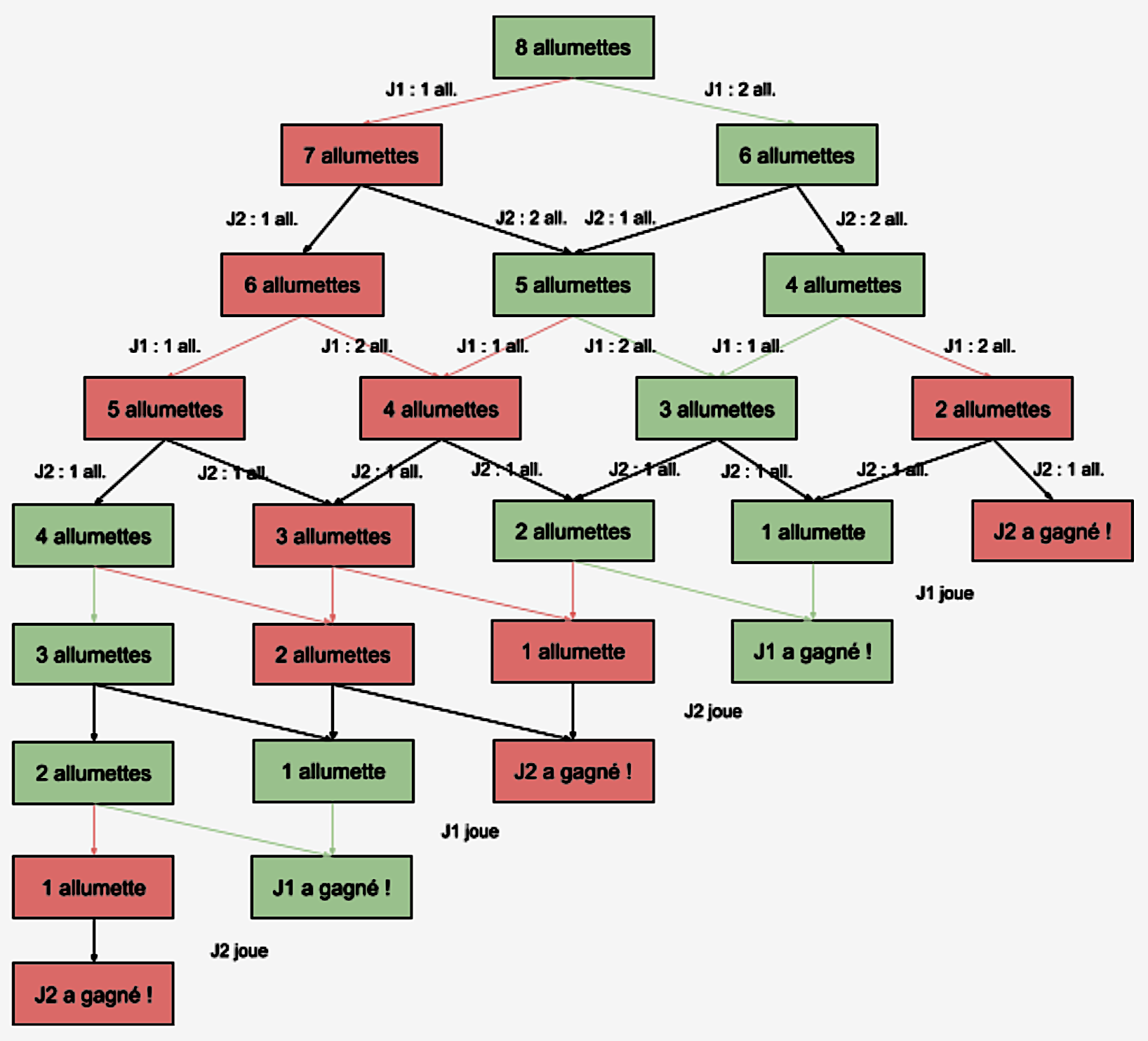
L'idée d'un arbre de jeu est de regarder l'ensemble des parties possibles et de tout explorer pour voir les issues des différentes parties possibles. Dessinons cet arbre :
Figure 5. Arbre du jeu de Nim |
Il y a deux joueur·ses : J1 et J2. Comment lire et utiliser un tel arbre de jeu qui liste toutes les parties possibles ? Il se lit de préférence à l'envers, on va remonter l'arbre depuis les feuilles (en bas) jusqu'à la racine (en haut). Toutes les cases où un·e joueur·se a gagné sont coloriées, en rouge si c'est J2 qui gagne, en vert si c'est J1. Ensuite, en remontant les étages, à chaque fois que c'est à J1 de jouer, si toutes les positions où iel peut aller sont rouges (i.e. victorieuses pour J2), on colorie la case en rouge : c'est une position perdante pour elle·lui. Par contre, si une des cases où iel peut aller est verte, cette position devient verte. En remontant ainsi l'arbre, on peut colorier toutes les positions, gagnantes pour l'un·e des deux joueur·ses. On remarque que, quand il reste trois ou six allumettes, la case est coloriée en vert (gagnante pour J1) si c'est à J2 de jouer ensuite, en rouge si c'est à J1 de jouer. Cela correspond bien à la stratégie trouvée dans la sous-section précédente.
Cet arbre donne le·la joueur·se qui a une stratégie gagnante mais il donne aussi la marche à suivre : ici pour J1 ne suivre que les flèches vertes.
On peut implémenter un algorithme qui utilise l'arbre de jeu avec la machine décrite ci-dessus. Il suffit de placer une bille de chaque couleur dans chaque verre. À chaque partie jouée, si la machine a gagné, on ne fait rien. Si la machine a perdu, on enlève la dernière bille jouée et on remet les autres dans les verres. Une fois qu'un verre est vide, on le retourne et si, dans une partie ultérieure, la machine arrive sur cette position, elle abandonne et on enlève la dernière bille jouée. C'est donc une exploration de l'arbre. Bien sûr, la machine finira par ne garder que les coups gagnants mais elle ne saisira pas les opportunités de victoire en cas d'erreur de l'adversaire (puisqu'elle abandonnera dès qu'elle se retrouvera dans une situation perdante, ce qui ne peut arriver que lorsqu'elle ne commence pas). Cette version, proposée par exemple par Marie Duflot [4], n'est pas de l'apprentissage par renforcement.
Si l'exploration de l'arbre est bien sûr très rapide pour le jeu ci-dessus, c'est parce que l'arbre est très petit (il tient complètement dans une demi-page A4). Dès que l'arbre devient plus grand, cette exhaustion de l'arbre est impossible à mener, même avec un ordinateur, pour des questions de temps de calcul et même pour des questions de stockage. Par exemple, le nombre de positions possibles au jeu d'échecs est d'environ 1046 et au jeu de Go d'environ 10170 alors que le nombre d'atomes dans l'univers est estimé à 1080. Et encore, on ne parle pas du nombre de parties possibles, encore plus gigantesque.
3.4 Apprentissage par renforcement
L'algorithme mis en place dans l'activité est un véritable algorithme d'apprentissage par renforcement, dans une version simplissime. Le principe de l'apprentissage par renforcement est le suivant : un agent fait des actions au hasard dépendant de l'état d'un environnement (éventuellement aléatoire d'ailleurs) et, en fonction du résultat obtenu, les choix sont récompensés ou punis, c'est-à-dire que les probabilités de faire lesdites actions dans le même état de l'environnement sont augmentées ou diminuées.
L'avantage de cet apprentissage provient de la non-nécessité pour le·la programmeur·se de connaître la stratégie optimale mais également de la non-nécessité de parcourir un arbre qui peut être immense. De plus, même si l'agent continuera à « jouer » au hasard, il apprendra rapidement à avoir un bon comportement et à le renforcer.
L'inconvénient provient du paramétrage (voir ci-dessous) et de la tendance d'un tel programme à s'enfermer dans un chemin efficace (trouvé par hasard, renforcé donc utilisé plus souvent donc renforcé donc etc.) même s'il en existe un plus efficace ailleurs. Des techniques sont disponibles pour contrer cet effet d'enfermement : on peut ainsi imposer au programme un peu d'exploration au hasard. La dose d'exploration est un choix et plus on en met, plus ça explore mais moins ça apprend vite.
3.5 Les paramètres du renforcement
Tout d'abord, il convient de remarquer que la machine n'apprend pas toute seule. L'algorithme d'apprentissage est un algorithme comme un autre. Et il y a plein de choix humains dans cet algorithme.
Premièrement, les récompenses et les punitions sont à la discrétion du·de la programmeur·se. Par exemple, ici, nous avons fait le choix d'initialiser avec deux billes de chaque couleur mais nous aurions pu en mettre trois, quatre ou plus. Cela changerait le degré de punition et de renforcement des premières parties. Nous pourrions également imaginer renforcer ou punir plus les coups de la fin que ceux du début. Nous pourrions aussi récompenser beaucoup plus (en ajoutant deux ou trois billes des couleurs jouées).
Deuxièmement, il faut fixer les objectifs et savoir ce qu'on punit et ce qu'on récompense. Dans un jeu, les choses sont assez claires, l'environnement est simple. On récompense les victoires, on punit les défaites. Mais, par exemple, s'il y a possibilité de match nul, est-ce qu'on le punit ou est-ce qu'on le récompense ? Si le match nul est un bon résultat (parce qu'il n'y a pas de stratégie gagnante, comme au morpion), il faut le récompenser. Mais s'il y a possibilité de victoire, existence d'une stratégie gagnante, il vaut mieux ne pas trop le récompenser, voire le punir. Et tout ceci est affaire d'essais et d'erreurs mais aussi de savoir-faire. Si on sort des jeux, les problèmes peuvent devenir encore plus compliqués : imaginons qu'on veuille faire prendre des décisions à une voiture autonome, à quels degrés punit-on et renforce-t-on les divers résultats ?
Enfin, dans l'activité ci-dessus, on peut se poser la question de l'adversaire. Vaut-il mieux jouer au hasard contre la machine ou jouer en connaissant la stratégie gagnante (mode expert) ? L'apprentissage s'en ressent. Il se trouve que c'est beaucoup plus efficace contre un·e adversaire qui connaît la stratégie gagnante.
Pour tester ces divers modes d'apprentissage et jouer avec tous ces paramètres, on pourra utiliser l'application développée par Éric Duchêne [5].
3.6 Et sans humain·e ?
On pourrait penser que nous sommes arrivés à une contradiction. D'un côté, l'apprentissage est efficace contre un·e expert·e. De l'autre, le grand intérêt de l'apprentissage par renforcement vient quand on ne connaît pas la stratégie optimale, donc quand il n'y a pas d'expert·e. Comment s'en sortir ?
Heureusement, il y a une solution : faire jouer la machine contre elle-même. Il n'y a que des avantages : plus besoin d'humain·e (pour jouer) donc gain de temps, plus besoin de connaître la stratégie a priori, une vitesse d'apprentissage très bonne.
Qu'entend-on par faire jouer la machine contre elle-même ? Soit on construit deux machines qui jouent l'une contre l'autre et sont punies ou récompensées de la même manière que dans la situation ci-dessus : celle qui gagne est récompensée, l'autre est punie. On peut alterner (ou pas) la machine qui commence. Soit, encore mieux car les situations de jeu et les coups possibles sont les mêmes pour les deux joueur·ses, on peut faire jouer les deux joueur·ses par la même machine. Il suffira de bien se souvenir quels sont les gobelets qui ont servi aux coups du·de la joueur·se 1 et quels sont ceux qui ont servi pour les coups du·de la joueur·se 2. A la fin de la partie, on récompense le côté qui a gagné et on punit le côté qui a perdu.
Avec un ordinateur, évidemment, cela est très pratique, et même absolument nécessaire quand on veut utiliser l'apprentissage par renforcement pour des jeux plus compliqués et qui demandent donc plus de parties.
Prenons un exemple :
- J1 joue : on pioche jaune dans verre 8, iel enlève une allumette.
- J2 joue : on est au verre 7, on pioche rouge, J2 enlève deux allumettes.
- J1 joue : on est au verre 5, on pioche rouge, J1 enlève deux allumettes.
- J2 joue : on est au verre 3, on pioche jaune, J2 enlève une allumette.
- J1 joue : on est au verre 2, on pioche rouge, J1 gagne.
On a donc la partie suivante :
- Verre 8 : jaune (J1)
- Verre 7 : rouge (J2)
- Verre 5 : rouge (J1)
- Verre 3 : jaune (J2)
- Verre 2 : rouge (J1)
Comme c'est J1 aui a gagné, on va punir les coups de J2 en enlevant les billes rouges jouées des verres 7 et 3 (on les met dans la réserve). Par contre, on va récompenser les coups des verres 8, 5 et 2 en remettant les billes dans les verres et en en ajoutant une de la même couleur prise dans la réserve.
3.7 Des variantes à foison
Avec la machine, il peut être intéressant de changer les règles du jeu et en particulier d'adopter des règles pour lesquelles la stratégie optimale n'est pas évidente. Ainsi faire jouer la machine contre elle-même permettra de dessiner cette stratégie optimale puisque la machine va s'en approcher. On peut alors dans un second temps discuter de cette stratégie optimale, voire démontrer rigoureusement qu'elle l'est ou comprendre pourquoi elle l'est.
Décrivons-en une. On part avec dix allumettes mais chaque joueur·se, à son tour, a le droit d'enlever une, trois ou quatre allumettes mais pas deux. Pour construire la machine, il faudra une troisième couleur de billes et, en prenant le code jaune = 1, rouge = 3, bleu = 4, initialiser la machine comme suit :
- verre 1 : que des jaunes (la machine ne peut prendre qu'une allumette)
- verre 2 : que des jaunes (la machine ne peut prendre qu'une allumette puisqu'elle n'a pas le droit d'en prendre deux)
- verre 3 : des jaunes et des rouges.
- verres 4 et suivants : des jaunes, des rouges, des bleues.
Dans chaque verre, l'initialisation se fait en mettant autant de billes de chaque couleur admissible. On peut ensuite lancer l'apprentissage, soit contre un·e humaine, soit, encore mieux, en faisant jouer la machine contre elle-même. Au bout de qinze à vingt parties, on devrait se retrouver avec :
- dans le verre 1, que des jaunes.
- dans le verre 2, que des jaunes.
- dans le verre 3, un mélange de jaunes et de rouges.
- dans le verre 4, une majorité de bleues.
- dans le verre 5, une majorité de rouges.
- dans le verre 6, une majorité de bleues.
- dans le verre 7, un mélange.
- dans le verre 8, une majorité de jaunes.
- dans le verre 9, un mélange.
- dans le verre 10, un mélange de jaunes et de rouges.
Pour simuler cette situation, on pourra aussi utiliser l'application Machine de Nim [5].
Série de 2 articles sur Intelligence artificielle et jeu de Nim
Article suivant 2/2 : « Intelligence artificielle et jeu de Nim (2/2) - Codage et applications ».
Références
[1] Alphago, documentaire de Greg Kohs, 2017, Deep Mind.
[2] Jouer au jeu de Nim contre une machine, vidéo de la MMI.
[3] Jeu de Nim et IA, déroulé d'atelier, MMI.
[4] Le jeu de Nim, déroulé d'activité, Marie Duflot.
[5] Machine Nim, application d'Eric Duchêne.
Pour citer cet article :
Intelligence artificielle et jeu de Nim (1/2) - Fonctionnement de l'apprentissage par renforcement, Olivier Druet, février 2023. CultureSciences Physique - ISSN 2554-876X, https://culturesciencesphysique.ens-lyon.fr/ressource/IA-Nim-1.xml