Activer le mode zen
Ressource au format PDF
Classification
Comment expliquer la formation des ondulations sur une feuille d'aluminium, autour d'un point d'impact de deux boules d'acier venant percuter la feuille en sandwich ?
04/02/2026
Travail réalisé dans le cadre des Olympiades de Physique, encadré par les enseignants Jean-Brice Meyer, Tristan Clément et Aurélie Elie.
Table des matières
Introduction
Lorsque l'on cogne deux boules de pétanque sur une feuille d'aluminium, des ondulations apparaissent autour du point d'impact. Nous avons voulu comprendre comment ces ondulations se forment.
L'idée de travailler sur ce projet nous est venue en regardant une vidéo (https://www.youtube.com/watch?v=I4cVADCfHQY) dans laquelle nous pouvions observer ces motifs. Comme nous voulions justement trouver un projet nous permettant de réfléchir à un phénomène facilement observable dans la vie de tous les jours, ce sujet répondait alors parfaitement à notre souhait.
En effet, nombreuses sont les questions que nous pouvons nous poser autour du phénomène observé : Est-ce que ces ondulations se forment pour des raisons mécaniques ? Est-ce que la feuille d'aluminium garde d'autres séquelles de l'impact ? Qu'observe-t-on avec des feuilles d'autres matériaux ? Autant de questions qui ont nécessité d'imaginer une démarche d'investigation au cours de laquelle nous avons dû explorer plusieurs pistes. C'est une partie de cette démarche que nous présentons dans cet article pour répondre à la problématique suivante :
Comment expliquer la formation des ondulations sur une feuille d'aluminium, autour d'un point d'impact de deux boules d'acier venant percuter la feuille en sandwich ?
L'intégralité de notre mémoire peut être rerouvé sur le site du concours des Olympiades de physique sous le titre « Tu tires ou tu pointes ? ».
1. Que voit-on si on fait varier la vitesse des billes lors de l'impact ?
1.1 Choix des matériaux
Nous avons pu découvrir ce phénomène dans une vidéo sur internet [1]. Bien entendu, aucune explication n'était donnée (sinon, cela aurait enlevé tout l'intérêt de faire ce projet).
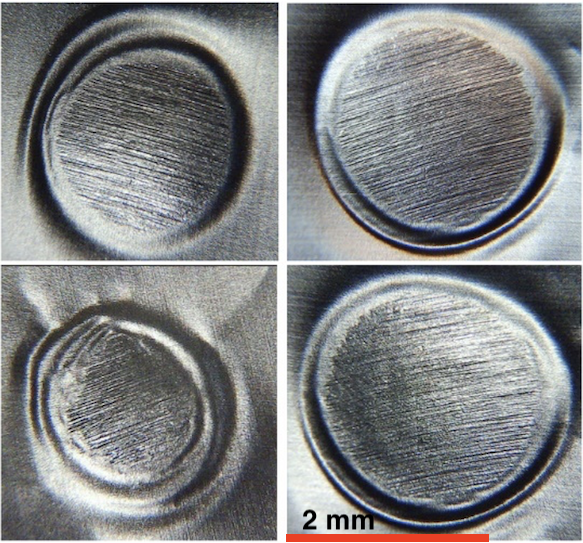
Nous avons alors décidé de reproduire le phénomène à l'aide de boules de pétanque, que nous avons simplement cognées l'une contre l'autre en intercalant du papier d'aluminium entre les deux. Le résultat est présenté sur la figure 1 : on observe quelques cercles concentriques.
|
Figure 1. Motifs obtenus sur une feuille d'aluminium après le choc entre deux boules de pétanque Pour toutes les images, l'échelle est donnée en bas de la figure : la barre rouge représente 2 mm Source : Geay, Nadaud, Xu, Jarrousse, Bouygues, Fauconnet, Chabasse, Durupt. |
On remarque que la zone de contact entre les deux boules est loin d'être ponctuelle. Il s'agit de la zone centrale, dans laquelle aucune vague n'apparaît. Cela nous a semblé étrange puisque les boules de pétanque étant sphériques, on s'attendait à avoir une surface de contact quasi ponctuelle. Mais en réalité, en regardant la boule de pétanque après l'impact, il s'avère que celle-ci s'est aplatie de manière irréversible lors du choc.
Dès lors, nous nous sommes dit qu'il serait intéressant que le contact soit plus ponctuel pour voir si l'on obtenait plus d'ondulations. Pour cela, nous avons recherché des boules de plus petit diamètre que les boules de pétanque, et avec des duretés plus grandes.
Nos boules de pétanque ont un diamètre de 7,3 cm, et des recherches nous ont appris que la dureté des boules de pétanque était de l'ordre de 35 HRC [2], ce qui correspond à 110 kg/mm2.
Dureté Rockwell
La dureté d'un matérieu peut être testée à l'aide d'un protocole appelé dureté Rockwell. Les essais sont réalisés en enfonçant une pointe conique en diamant ou une bille en acier trempé polie dans le matériau étudié. Pour obtenir une valeur de dureté Rockwell, on mesure la pénétration rémanente et donc la contrainte irréversible (le matériau ne retrouve pas sa forme originelle : on n'est plus dans le domaine élastique, mais dans le domaine plastique).
En cherchant sur internet, nous avons vu que les billes utilisées dans les roulements à billes pouvaient avoir des duretés nettement plus grandes, entre 60 et 64 HRC, soit pratiquement deux fois plus que celle des boules de pétanque. Nous en avons alors acheté quatre, qui sont des billes de 4 cm de diamètre (venant de roulements à billes utilisés généralement pour des camions). Il s'agit de billes en acier au chrome (AISI 52100) dont voici les caractéristiques :
|
Module d'élasticité |
190-210 GPa |
|
Coefficient de Poisson |
0,27-0,30 |
|
Dureté Rockwell C |
62 |
|
Densité |
7,81 |
|
Coefficient de dilatation thermique à 23-280°C |
11,9 µm/m°C |
|
Conductivité thermique (acier typique) |
46,6 W/mK |
Une fois reçues, nous les avons cognées, et effectivement, suite à l'impact, aucune trace, même pas une rayure n'est constatée sur la surface de la boule.
Et lorsque nous les cognons en intercalant une feuille de papier aluminium entre les deux, voici ce que nous obtenons, figure 2.
|
Source : Geay, Nadaud, Xu, Jarrousse, Bouygues, Fauconnet, Chabasse, Durupt. |
Alors plusieurs questions se posent : en particulier sur les ondulations obtenues. Leur nombre ainsi que les rayons ou leurs amplitudes varient-ils en fonction de la vitesse à laquelle les boules se cognent ?
Des premières expériences très qualitatives nous ont montré que plus l'on cogne les boules avec une grande vitesse, et plus on observe des vagues concentriques. Alors, pour étudier cela quantitativement, il a fallu construire un dispositif expérimental adapté, permettant de contrôler la vitesse au moment de l'impact.
1.2 Dispositif expérimental et premières observations en fonction de la vitesse
1.2.1 Dispositif expérimental
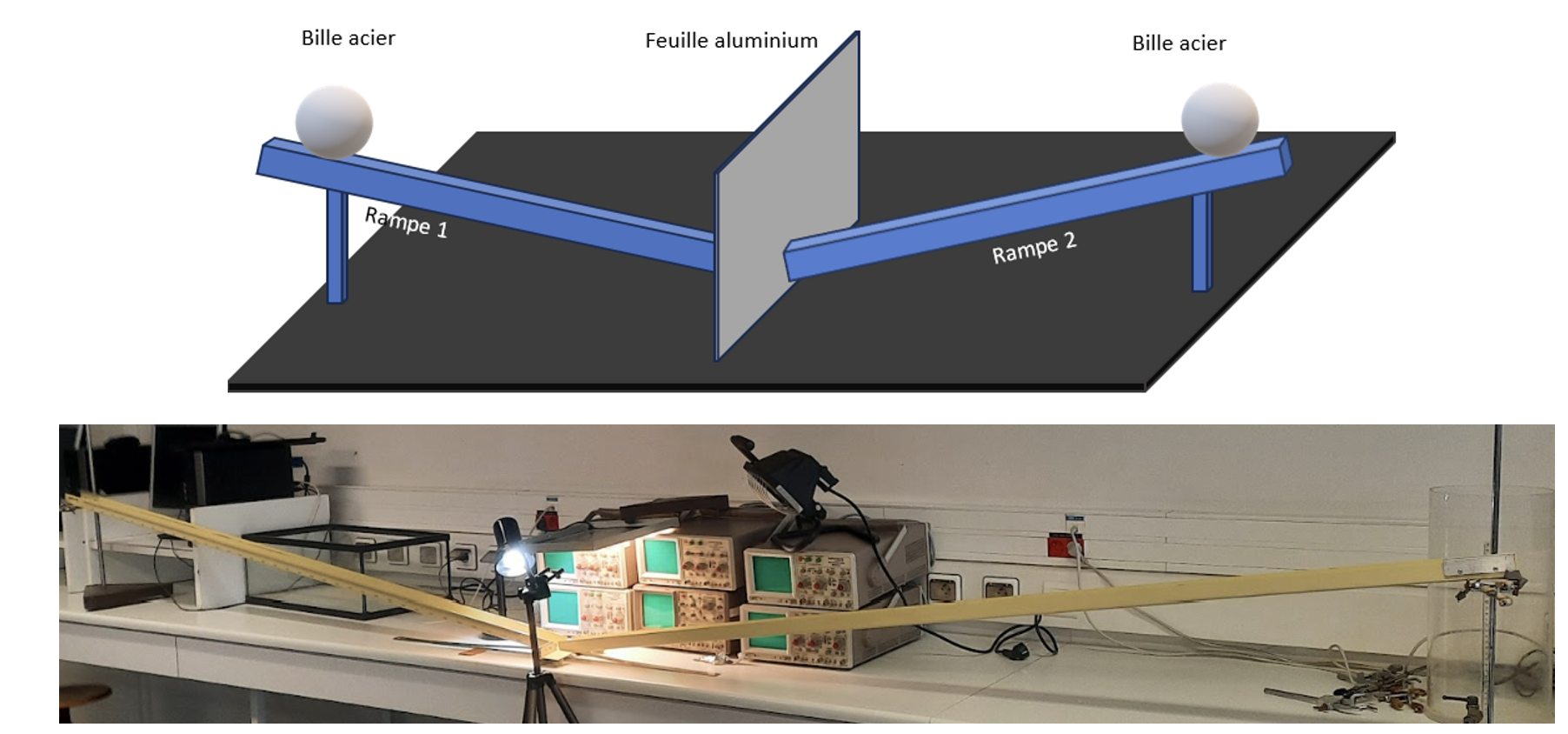
Notre premier dispositif était composé de deux rampes permettant de guider les billes jusqu'à leur contact, figure 3.
|
Figure 3. Schéma et photo du premier dispositif expérimental Source : Geay, Nadaud, Xu, Jarrousse, Bouygues, Fauconnet, Chabasse, Durupt. |
Ce dispositif présentait néanmoins deux problèmes :
- Les billes étaient lâchées à la main et il fallait alors de la réussite pour que le choc se passe exactement à l'endroit voulu, c'est-à-dire à l'endroit où était disposée la feuille d'aluminium.
- D'autre part, le choc entre les billes n'était pas frontal. Une fois que les billes se cognaient, elles avaient du mal à repartir en arrière. Or nous comptions faire des études énergétiques dans le but de connaître la quantité d'énergie que les billes perdaient lors du choc.
Nous avons alors choisi de confectionner un autre dispositif expérimental.
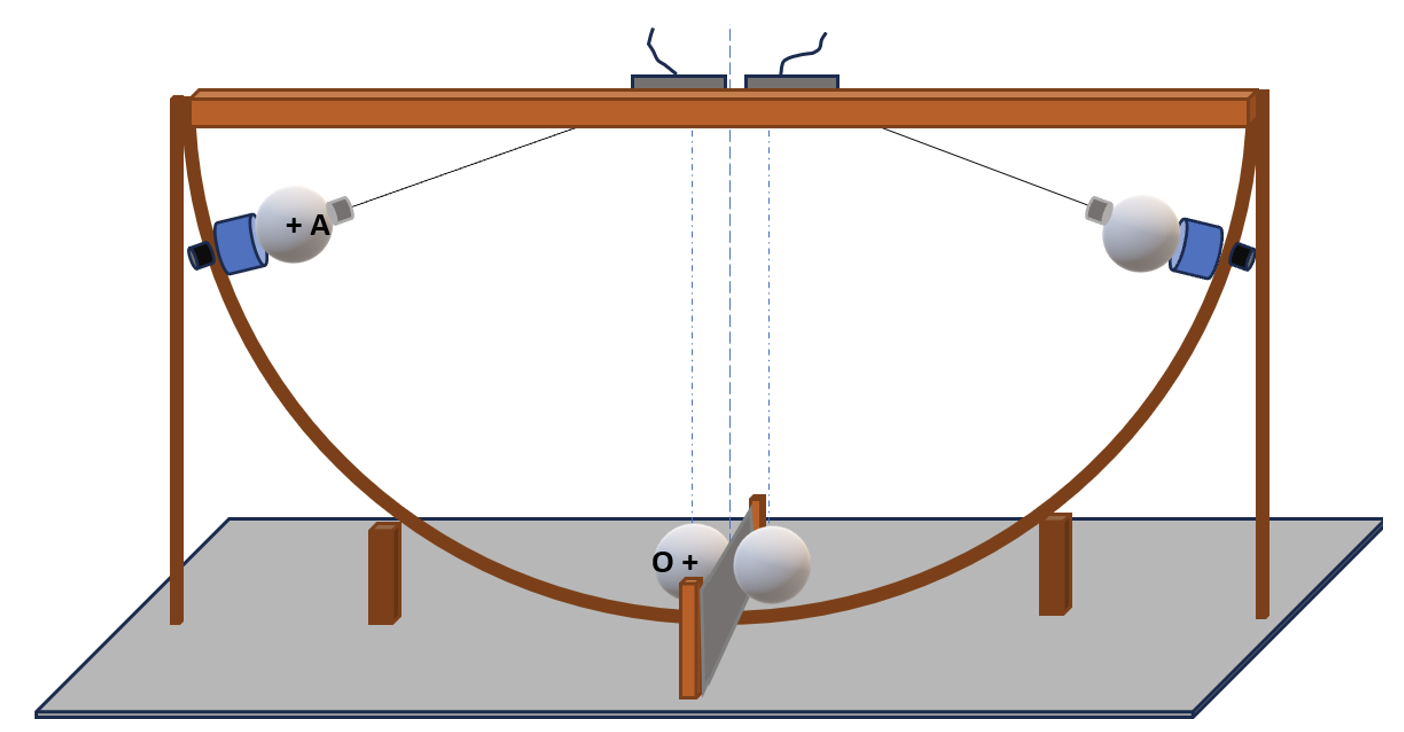
Dans ce dispositif, figure 4, les boules sont maintenues par deux électroaimants contrôlés par le même circuit électrique, ce qui permet de lâcher les billes en même temps. Nous pouvons faire varier la hauteur des électroaimants de façon à faire varier la vitesse des billes au moment de l'impact.
|
Figure 4. Schéma du second dispositif expérimental Source : Geay, Nadaud, Xu, Jarrousse, Bouygues, Fauconnet, Chabasse, Durupt. |
Comme la planche arrondie est un arc de cercle, nous avons dû faire en sorte que la longueur des fils maintenant les billes soit ajustable. Les deux éléments en gris en haut du dispositif permettent également d'ajuster le point de fixation des deux fils par rapport à la direction horizontale, de sorte que lors du choc, les fils soient dans des directions verticales (comme le montrent les lignes en pointillés sur la figure 4). Enfin, le papier d'aluminium est maintenu grâce à deux morceaux de bois dans lesquels nous avons fait une incision pour y glisser la feuille.
Les premiers lâchers que nous avons filmés ont pu mettre en évidence que le choc sur le papier d'aluminium se faisait le plus souvent à l'endroit prévu, mais pas toujours. Le problème vient en particulier de l'attache du fil au niveau des billes. Comme il n'a pas été possible de percer la bille (c'est l'inconvénient d'avoir choisi de travailler avec une grande dureté), nous avons collé un élément métallique sur la bille, doté d'un pas de vis dans lequel nous avons vissé un crochet. C'est à ce crochet qu'est attaché le fil.
Nous avons alors remarqué que parfois, la bille arrivait de telle sorte que l'axe du crochet n'était pas selon la direction du fil, ce qui engendrait alors un retard d'une bille par rapport à l'autre. Nous avons alors dû, lors de nos mesures tenir compte de cela pour ne prendre en compte que les chocs qui se faisaient dans le plan médian.
Nous réfléchissons en parallèle à modifier l'attache des fils pour ne plus être gênés par cela.
Maintenant que nous avons un dispositif expérimental qui nous paraît satisfaisant (même s'il est perfectible), nous pouvons l'exploiter.
1.2.2 Influence de la vitesse sur la figure obtenue
Voyons en particulier ce que nous observons sur le papier d'aluminium lorsqu'on modifie la vitesse des billes lors de l'impact. La vitesse des billes lors de l'impact est connue en appliquant simplement la conservation de l'énergie mécanique, en supposant que les frottements fluides sont négligeables, figure 4.
$$ E_m\big(O\big) = E_m\big(A\big) $$
$$ \Leftrightarrow E_c\big(O\big) + E_p\big(O\big) = E_c\big(A\big) + E_p\big(A\big) $$
$$ \Leftrightarrow \frac{1}{2} m v_o^2 + 0 = 0 + m g h_A $$
$$ \Leftrightarrow v_o = \sqrt{2 g h_A} $$
Voici ce que nous observons pour différentes vitesses des billes au moment du choc, figure 5.
|
Pour toutes les images, l'échelle est donnée en haut de la figure : la barre rouge représente 1 mm. Source : Geay, Nadaud, Xu, Jarrousse, Bouygues, Fauconnet, Chabasse, Durupt. |
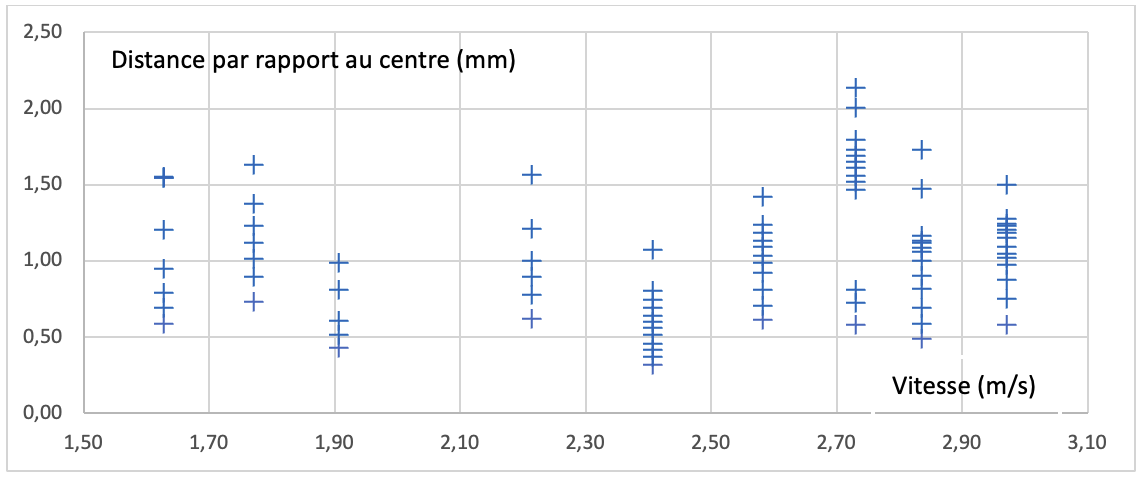
Nous avons relevé les rayons des différentes ondulations pour chacune des vitesses des billes au moment de l'impact, figure 6.
|
Source : Geay, Nadaud, Xu, Jarrousse, Bouygues, Fauconnet, Chabasse, Durupt. |
En essayant de tirer des conclusions générales à partir de ce graphique, nous ne trouvons aucune évolution logique à formuler. Ce qui nous intriguait était aussi le fait que visuellement, nous observions bien moins d'ondulations à l'œil nu qu'au microscope. Finalement, en cherchant à comprendre cette différence d'observation, nous nous sommes rendus compte que cela était dû à l'éclairage de la feuille lors de l'observation au microscope. Nous avions un éclairage en incidence frontale : la lumière était réfléchie aussi bien par le sommet de l'ondulation que par le creux. Cela donnait l'impression d'observer plus d'ondulations, à tort. Nous avons alors par la suite éclairé les figures avec un éclairage non frontal.
Ces premières observations soulevaient déjà des questions, telles que :
- Y a-t-il un rapport entre l'énergie communiquée au papier d'aluminium et la figure obtenue ? Pour cela, il nous fallait mesurer l'énergie transmise au papier d'aluminium lors de l'impact.
- Peut-on évaluer la force de pression subie par l'aluminium lors du choc pour évaluer la déformation engendrée ?
Par ailleurs, comme nos clichés manquaient de régularité dans les ondulations, nous nous sommes dits que nous pouvions réaliser de nouveaux impacts en contrôlant davantage les conditions expérimentales. Nous en avons profité pour faire différentes mesures quantitatives, le plus précisément possible. Les réglages demandaient vraiment une attention très minutieuse et chronophage. Nous avons alors réalisé l'expérience avec quatre hauteurs de lâcher différentes. Voici, figure 7, quelques clichés obtenus, l'étalon en rouge mesure 1 mm.
|
Source : Geay, Nadaud, Xu, Jarrousse, Bouygues, Fauconnet, Chabasse, Durupt. |
2. Étude mécanique
2.1 Compression de l'aluminium
Lors du choc par les billes, le papier d'aluminium subit localement une grande pression, qui pourrait alors le déformer et révéler ces cercles. Il s'aplatirait alors à l'endroit du choc, et comme le volume de la matière resterait malgré tout constant, l'épaisseur de la feuille d'aluminium diminuerait lors de l'impact, ce qui augmenterait la surface. On pourrait modéliser cela de la façon suivante : à l'endroit de l'impact, on passerait d'un cylindre de caractéristiques géométriques e, h, à e', h', tel que le montre le schéma figure 8.
|
Source : Geay, Nadaud, Xu, Jarrousse, Bouygues, Fauconnet, Chabasse, Durupt. |
Cette augmentation de surface pousserait alors le papier aluminium sur le côté, et pourquoi pas, conduirait à son plissement sous forme de vagues concentriques. Et d'autre part, la compression temporaire pourrait être élastique. On pourrait alors avoir une oscillation de la géométrie de l'aluminium, qui pourrait être à l'origine d'ondes qui se propageraient depuis le point d'impact vers la périphérie.
Alors voyons maintenant si ces hypothèses sont possibles, en évaluant la déformation subie par le papier d'aluminium lors du choc.
On peut calculer la force exercée par une bille sur le papier d'aluminium
|
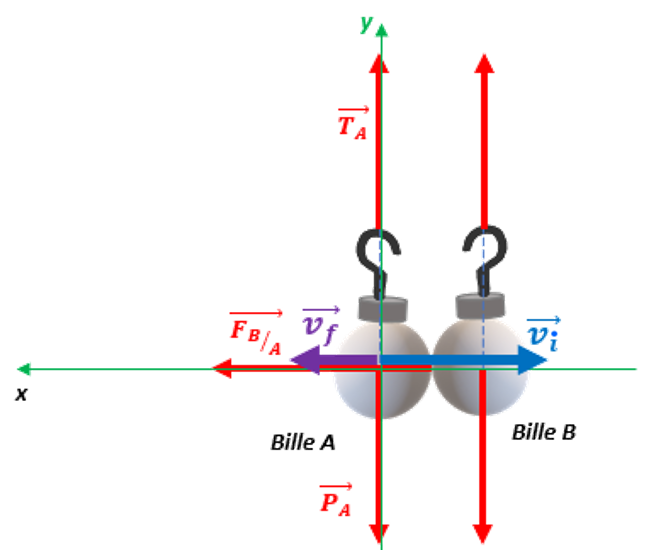
Figure 9. Schéma représentatif des forces appliquées et des vitesses de la bille A avant et après l'impact Source : Geay, Nadaud, Xu, Jarrousse, Bouygues, Fauconnet, Chabasse, Durupt. |
D'après la deuxième loi de Newton appliquée à la bille A, la bille passe d'une vitesse \( \overrightarrow{v_i}\) immédiatement avant le choc , à une vitesse \( \overrightarrow{v_f}\) immédiatement après le choc, durant la durée du choc \(\Delta t\), figure 9.
L'accélération de la bille lors du choc est donc
$$ \overrightarrow{a} = \frac{\Delta \overrightarrow{v}}{\Delta t} = \frac{\overrightarrow{v_f} - \overrightarrow{v_i}}{\Delta t} $$
Projetée sur l'axe (Ox), on a : \( a_x = \frac{v_f +v_i}{\Delta t} \)
En appelant \( \overrightarrow{P} \) la force de pesanteur appliquée à la bille, et \( \overrightarrow{F} \) la force exercée par le papier aluminium sur la bille et \(\overrightarrow{T}\) la tension exercée par le fil,
$$ \overrightarrow{P}+\overrightarrow{F}+\overrightarrow{T} = m \overrightarrow{a} $$
Comme \( P_x = 0, T_x = 0\), on en déduit que
$$ F_x = m \frac{v_f + v_i}{\Delta t} $$
Du fait de la présence des deux billes, on peut donc dire que la feuille d'aluminium subit une force égale à deux fois \( F_x \) c'est-à-dire \( F = 2 m \frac{v_f +v_i}{\Delta t} \)
Les vitesses \(v_f\) et \(v_i\) peuvent être déterminées en mesurant la hauteur \(h\) de laquelle s'élance la boule de départ, et en notant la hauteur \(h'\) à laquelle elle remonte. En effet, en appliquant la conservation de l'énergie cinétique dans un premier temps avant le choc :
$$ E_c = \frac{1}{2} mv_i^2 = mgh \Longleftrightarrow v_i = \sqrt{2 gh} $$
De même, après le choc : \( v_f = \sqrt{2 g h'} \)
Donc :
$$ F=2m \frac{\sqrt{2gh'}+ \sqrt{2 gh}}{\Delta t} $$
Nous connaissons déjà les hauteurs \(h\) et \(h'\), mais qu'en est-il de la durée du choc ?
En filmant le choc avec une caméra à 1000 images par seconde, nous n'arrivons pas à avoir une seule image pile au moment de l'impact. Le choc dure donc un temps sûrement très inférieur à 1 ms.
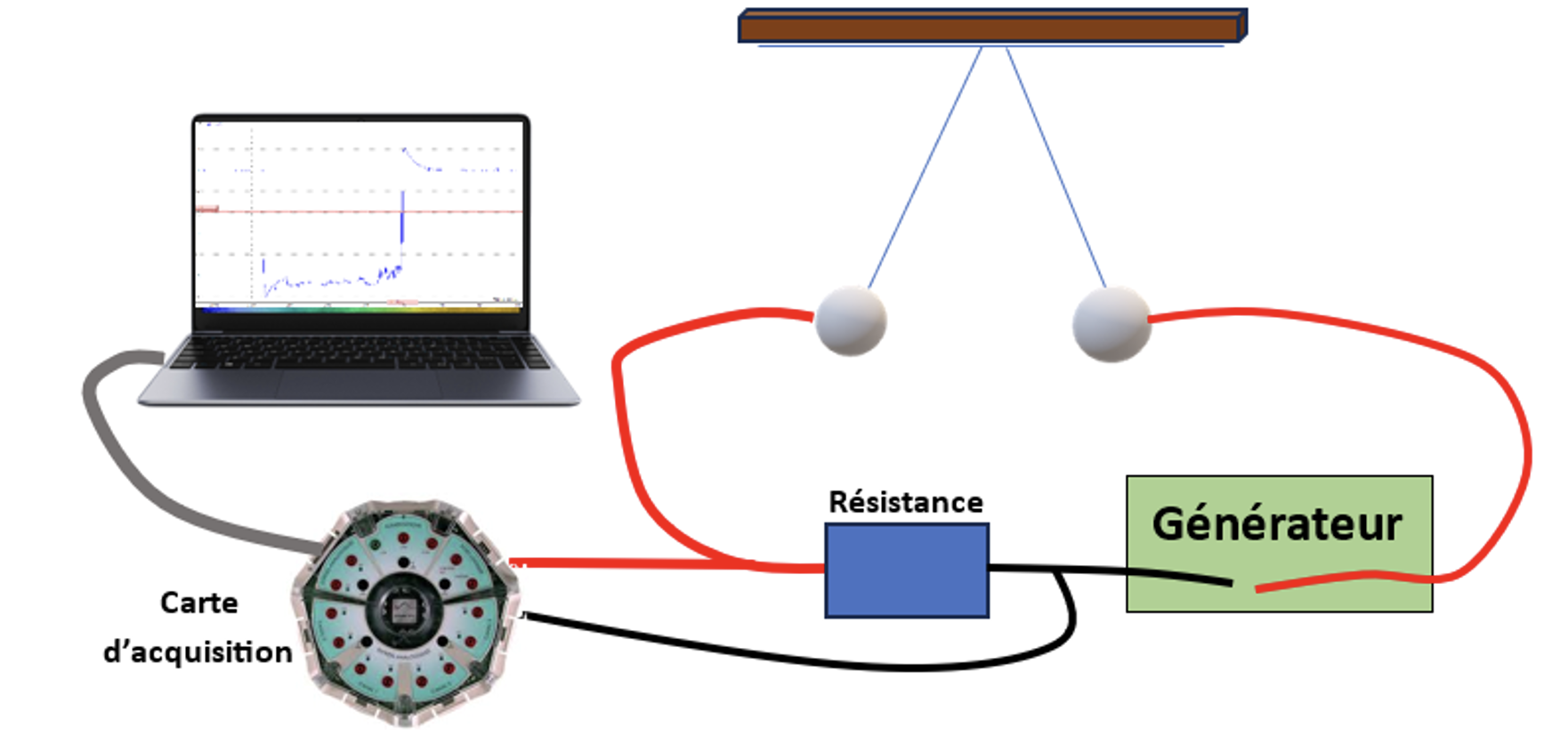
Pour mesurer cette durée, nous avons eu l'idée de faire un circuit électrique qui se ferme lorsque les billes se touchent. Le circuit est illustré sur le schéma suivant, figure 10.
|
Figure 10. Schéma du dispositif expérimental utilisé pour mesurer la durée de l'impact des billes Source : Geay, Nadaud, Xu, Jarrousse, Bouygues, Fauconnet, Chabasse, Durupt. |
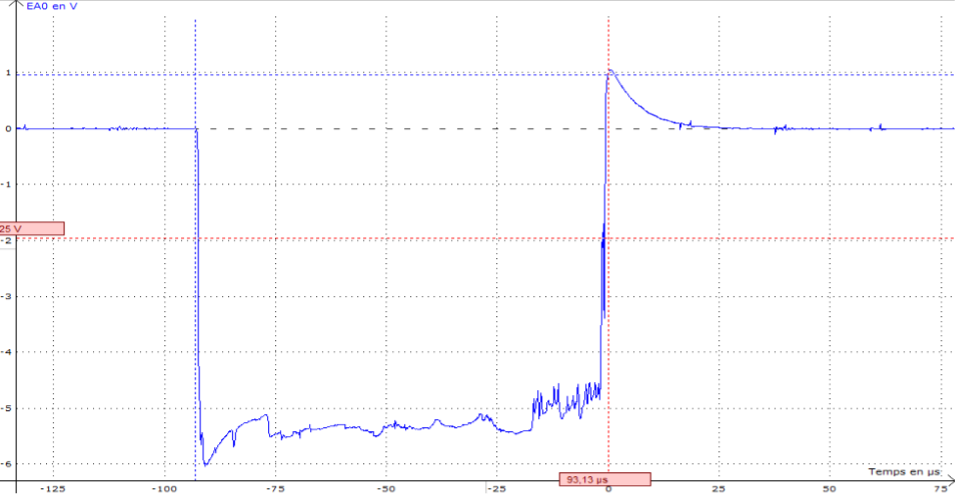
Nous avons alors réalisé la mesure de la durée du contact sans papier d'aluminium entre les boules, et avec papier d'aluminium entre les boules. Un exemple de mesure de la durée du choc avec papier d'aluminium entre les 2 boules est donné figure 11, ici on a trouvé environ 93 \(\mu\)s.
|
Figure 11. Mesure de la durée du choc des billes obtenue sur Latis Pro Source : Geay, Nadaud, Xu, Jarrousse, Bouygues, Fauconnet, Chabasse, Durupt. |
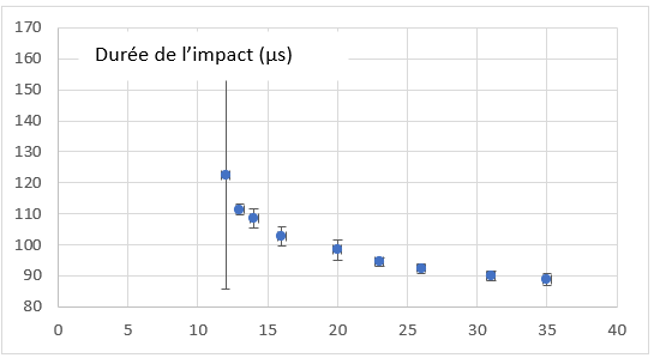
La figure 12 montre comment évolue la durée de contact (en \(\mu\)s) en fonction de la hauteur des billes (en cm) au départ, avec le papier aluminium entre les billes.
|
Source : Geay, Nadaud, Xu, Jarrousse, Bouygues, Fauconnet, Chabasse, Durupt. |
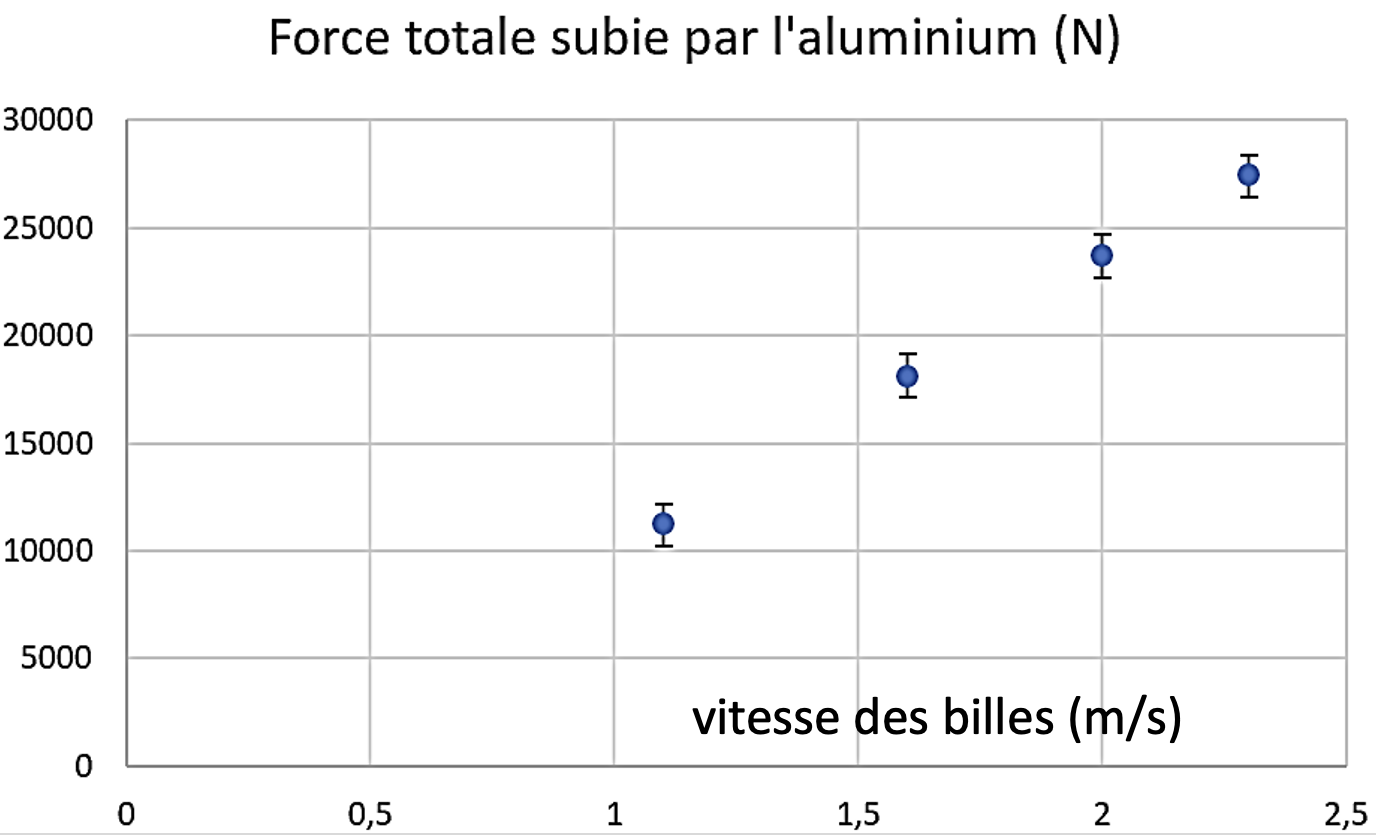
On peut donc tracer la force subie par chaque bille en fonction de la vitesse des billes au point d'impact, figure 13.
|
Figure 13. Évolution de la force subie par l'aluminium en fonction de vitesse des billes lors de l'impact Source : Geay, Nadaud, Xu, Jarrousse, Bouygues, Fauconnet, Chabasse, Durupt. |
2.2 Une onde qui se propage ?
On pourrait imaginer que les déformations se fassent de façon pseudo-périodiques suite à l’impact, ce qui peut alors être à l’origine d’ondes au sein de la feuille d’aluminium conduisant aux ondulations autour de la zone d’impact. Le choc pourrait provoquer l’apparition d’ondes transversales.
La clarté des images obtenues permet de se rendre compte d'une certaine régularité dans la position des vagues concentriques, comme le montre l'image figure 14.
|
Figure 14. Mise en évidence de la régularité des ondulations Source : Geay, Nadaud, Xu, Jarrousse, Bouygues, Fauconnet, Chabasse, Durupt. |
Cette onde transversale serait alors issue de la vibration de l’épaisseur et de la surface de l’aluminium lors de l’impact. Nous avons pu aller plus loin dans l'observation et l'analyse des figures obtenues. En effet, nous avons eu l'occasion de réaliser des observations de nos clichés au SP2MI (Faculté des Sciences Physiques Mathématiques Mécaniques et Informatiques), avec Frédéric Pailloux, chercheur à l'Université de Poitiers.
Un microscope ultra-performant nous a permis d'observer nos images en trois dimensions, par un jeu de focalisation en fonction de l'intensité de la lumière réfléchie, figures 15, 16 et 17.
|
Figure 15. Prise en main du microscope Source : Geay, Nadaud, Xu, Jarrousse, Bouygues, Fauconnet, Chabasse, Durupt. |
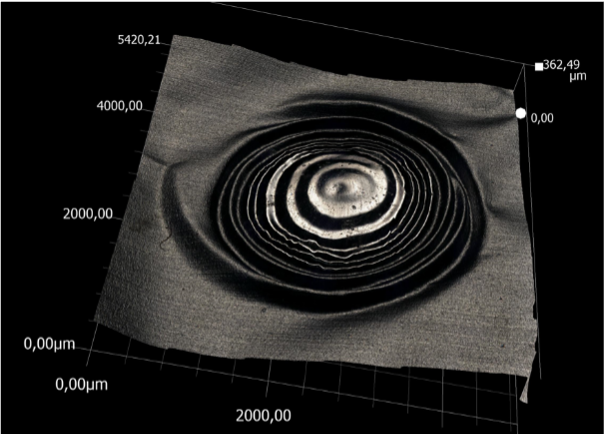
Figure 16. Figure complète en 3D scannée par le microscope Source : Geay, Nadaud, Xu, Jarrousse, Bouygues, Fauconnet, Chabasse, Durupt. |
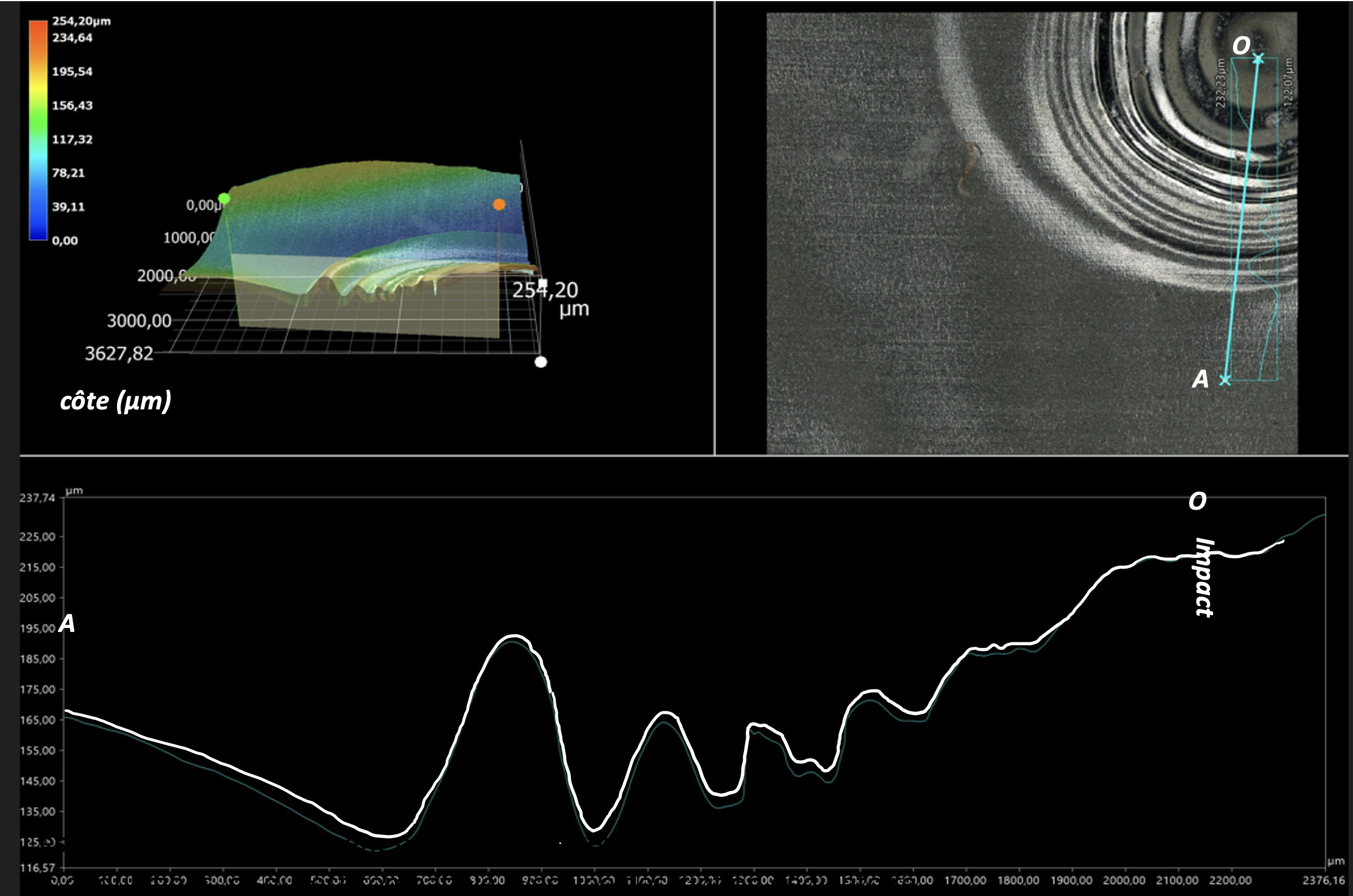
|
Source : Geay, Nadaud, Xu, Jarrousse, Bouygues, Fauconnet, Chabasse, Durupt. |
Nous voyons sur l'image que l'ondulation de plus forte amplitude se trouve la plus éloignée du point d'impact. Or, si on imagine une description ondulatoire, on peut penser que cette ondulation correspond à celle qui s'est formée au moment du choc puis qui s'est propagée vers l'extérieur. La feuille d'aluminium, au niveau du point d'impact, a ainsi pu vibrer au cours du temps, avec une amplitude de plus en plus faible. L'image que nous observons correspondrait alors au moment où la première ondulation, formée immédiatement après le choc, s'est propagée le plus loin, et la dernière ondulation formée après le choc s'est propagée le moins loin, avant que tout ne se fige. Les amplitudes observées sont cohérentes avec une description ondulatoire.
Nous avons voulu pousser l'analyse plus loin et savoir si l'on pouvait faire un lien entre l'augmentation de surface de l'aluminium due à la présence des ondulations, et l'augmentation de la surface de la zone de contact due à la compression de l'aluminium, que nous avions évaluée en amont (de l'ordre de 6% pour les plus grandes vitesses des billes au moment de l'impact). Pour cela, nous avons dû évaluer l'augmentation de la surface de l'aluminium due à la présence des ondulations.
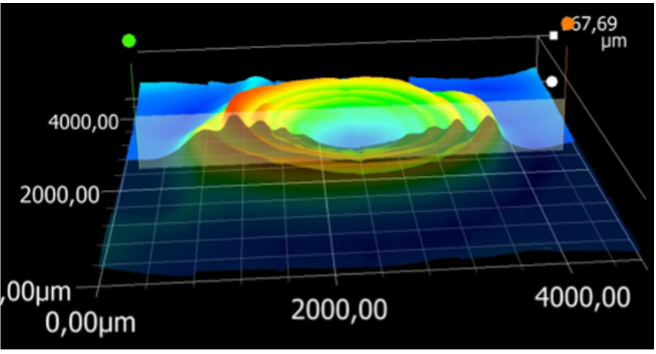
Voici la démarche que nous avons suivie pour faire cela en prenant exemple sur cette figure 18.
|
Source : Geay, Nadaud, Xu, Jarrousse, Bouygues, Fauconnet, Chabasse, Durupt. |
Nous avons découpé la figure obtenue en un ensemble de cônes tronqués, figure 19. Cela était d'autant plus facile à faire que nous possédions les coordonnées précises de la feuille d'aluminium en 3D.
|
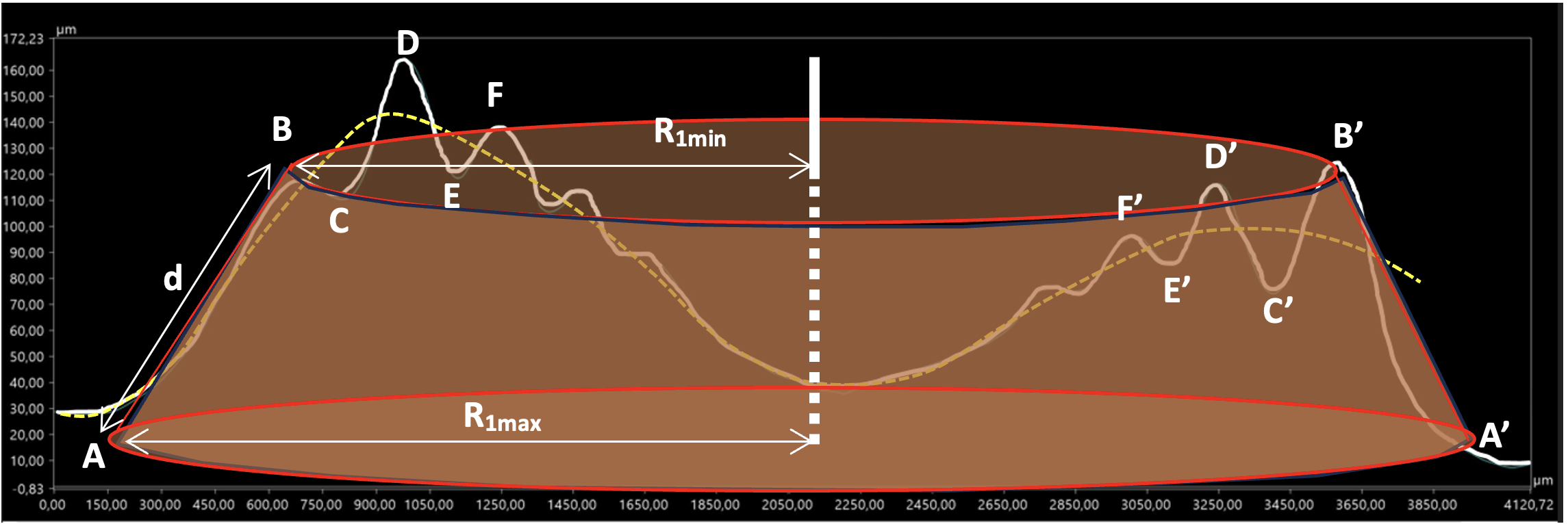
Figure 19. Découpe du profil des ondulations en un ensemble de cônes tronqués Source : Geay, Nadaud, Xu, Jarrousse, Bouygues, Fauconnet, Chabasse, Durupt. |
Connaissant les coordonnées des extrémums (A, B, C, etc.) de la courbe blanche montrant les ondulations en coupe, nous avons modélisé les ondulations par un ensemble de cônes tronqués. Par exemple, sur la figure 19, nous avons représenté un premier cône tronqué (en rouge) s'appuyant sur les segments [AB] et [A'B'].
Nous avons fait de même en représentant un cône tronqué s'appuyant sur les segments [BC] et [B'C'], etc. Comme on peut voir que BC et B'C' ne sont pas symétriques par rapport à un axe vertical passant par le centre de la figure, nous avons pris les valeurs moyennes des coordonnées de B et B' et de C et C' pour représenter le cône en question.
Chaque cône \(i\) a alors une surface égale à \( S_i = \pi \times d_i \times (Ri_{max} +Ri_{min}) \)
La surface totale de la figure est donc : \( S_{totale} = \sum_i \pi \times d_i \times (Ri_{max} +Ri_{min} ) \)
Le modèle d'une compression élastique est-il possible ?
Le point le plus important que nous avons mis en doute est celui qui consistait à dire que le choc des billes avec la feuille d'aluminium provoquait une compression élastique, et donc une élongation élastique de la surface de l'aluminium. En effet, nous avons supposé que la compression de l'aluminium lors de l'impact était élastique, cela suppose alors que l'épaisseur de l'aluminium après l'impact retrouve sa valeur initiale. Et si tel est le cas, comment expliquer l'augmentation de surface après l'impact ? Pour y voir plus clair, nous avons voulu savoir si oui ou non l'épaisseur de l'aluminium est modifiée après l'impact.
Pour cela, nous avons à nouveau fait dix impacts sur dix feuilles d'aluminium. Nous avons alors découpé l'aluminium autour des impacts et nous avons mis ces bandes d'aluminium dans de la résine. Une fois la résine durcie, nous avons pu découper l'aluminium au milieu de la figure des ondulations. Nous avons alors pu observer la tranche de l'aluminium pour chacun des dix impacts au microscope. Une des images obtenues est présentée figure 20.
|
Figure 20. Observation au microscope des ondulations selon la tranche Source : Geay, Nadaud, Xu, Jarrousse, Bouygues, Fauconnet, Chabasse, Durupt. |
Nous n'observons aucune diminution permantente de l'épaisseur. Donc si le choc a diminué l'épaisseur, cela n'a été que temporaire et il semble donc bien que la compression et donc l'élongation de l'aluminium soit élastique. Autrement dit, les ondulations ont dû se former sans augmentation de surface de l'aluminium. Cela signifie, de fait, que l'aluminium à l'extérieur a été attiré vers la zone de l'impact. Il faudrait que nous puissions mettre des jauges de contrainte sur l'aluminium, ou des repères pour constater cela expérimentalement. Mais cela s'avère compliqué à réaliser expérimentalement au lycée et nous devons chercher si un laboratoire pourrait nous aider dans cette tâche, car nous avons calculé qu'une variation de 6% de la surface s'accompagne d'une variation de seulement 3% du rayon de la figure, soit une valeur trop faible pour que nous puissions l'observer à l'aide de repères que nous ferions sur l'aluminium. Quoi qu'il en soit, les mesures montrent qu'une description ondulatoire est tout à fait possible, car la déformation élastique pourrait se traduire par une certaine oscillation de l'épaisseur de l'aluminium, conduisant à des ondulations transversales d'amplitudes de plus en plus faibles.
Etude à l'aide d'une simulation : une onde qui naît d'une antisymétrie…
Par ailleurs, nous avons rencontré Thibault de Rességuier, directeur de recherche à l'ENSMA, spécialisé dans la physique des chocs.
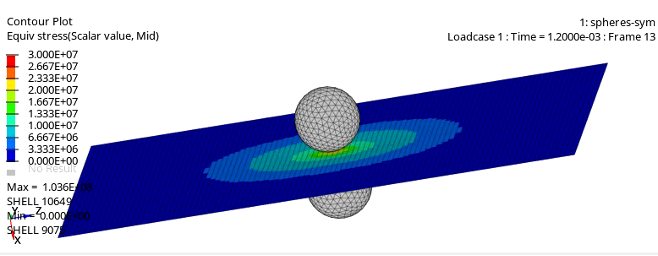
Lors de notre échange, il a été intéressant de discuter de certaines similitudes entre les figures obtenues avec le papier d'aluminium, et de figures issues par exemple de chocs entre une météorite et le sol terrestre. Très intéressé par notre projet, Thibault de Rességuier a réalisé des simulations pour voir ce que peut engendrer le choc de billes d'acier sur l'aluminium. Ces simulations ont montré que si le choc est parfaitement symétrique de part et d'autre de la feuille, les contraintes engendrées restent dans le plan de la feuille, sans provoquer l'apparition d'ondes transversales, figure 21.
|
Source : Geay, Nadaud, Xu, Jarrousse, Bouygues, Fauconnet, Chabasse, Durupt. |
Par contre, si le choc n'est pas parfaitement symétrique, et c'est forcément le cas dans nos expériences car on ne peut pas régler le dispositif au dixième de millimètre près, la simulation montre effectivement qu'une onde transversale doit apparaître et se propager sur la feuille. Monsieur de Rességuier nous a proposé de travailler avec lui pour poursuivre cette simulation, afin que les paramètres soient au plus proche de nos expériences, ce que nous ne manquerons pas de faire.
Après tant d'indices, a-t-on moyen de vérifier expérimentalement que le phénomène a une origine ondulatoire ?
Cela nous a semblé possible de reproduire l'expérience non pas sur une feuille d'aluminium, mais sur des feuilles d'autres matériaux tels que des feuilles de cuivre, d'acier et de laiton de différentes épaisseurs, que nous avons pu nous procurer. Pour une épaisseur donnée, nous nous attendons à observer des ondulations intercalées de distances différentes d'un matériau à l'autre. En effet, comme la célérité des ondes dépend du milieu dans lequel l'onde se propage, des matériaux différents pourraient conduire à des longueurs d'onde différentes.
Un résultat obtenu avec une feuille de cuivre est visible sur la figure 22.
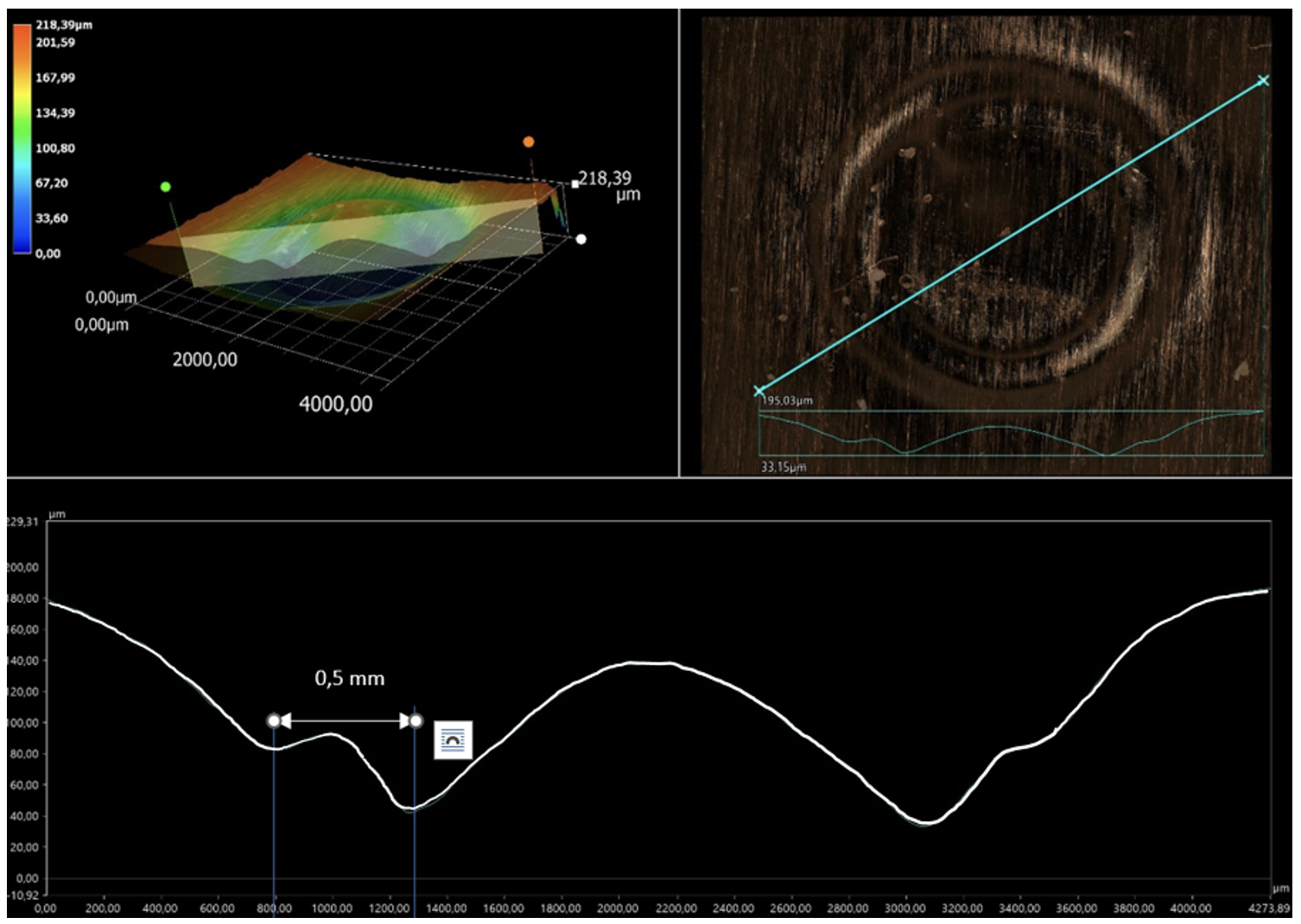
|
Figure 22. Image au microscope et profil des ondulations sur une feuille de cuivre Source : Geay, Nadaud, Xu, Jarrousse, Bouygues, Fauconnet, Chabasse, Durupt. |
Avec la feuille de cuivre, nous observons bien moins d'ondulations qu'avec l'aluminium, et si on s'en tient à une description ondulatoire, il semblerait que la longueur d'onde doit être de l'ordre de 0,5 mm, au lieu des 0,2 mm observés en moyenne sur les feuilles d'aluminium.
On pourrait se réjouir d’observer une différence, mais ce n’est pas le cas. En effet, nous avons recherché quelle devrait être la célérité des ondes transversales dans l'aluminium et le cuivre et il s'avère que la célérité de ces ondes dans l'aluminium est plus grande que dans le cuivre, ce qui devrait conduire à une longueur d’onde plus grande dans l'aluminium que dans le cuivre (\( \lambda = c T \)).
Pour compléter la discussion à propos des expériences réalisées avec des feuilles d’autres métaux, les expériences réalisées avec les feuilles d'acier n’ont montré aucune ondulation. Il est même pratiquement impossible d'observer le point d'impact des billes. Quant aux feuilles de laiton, on arrive à observer un point d'impact, mais pas d’ondulation.
En étudiant les caractéristiques de ces différents matériaux, il paraît évident que cela est dû à leur différentes limites plastiques. Nous avons pu lire que la limite plastique de l'acier est plus élevée que celles de l'aluminium et du cuivre. Ces valeurs traduisent la capacité qu'a le matériau à se déformer de façon réversible sous l’action d’une contrainte limite. La limite plastique élevée de l'acier peut ainsi permettre aux perturbations de se propager sans déformer irréversiblement l'acier. Mais cela ne répond pas à l'interrogation que nous nous sommes posée sur les valeurs des longueurs d’onde sur les feuilles d’aluminium et de cuivre.
Il y a un autre point qui pose question dans le cadre d’une description ondulatoire : puisque nous observons des ondulations sur la feuille d’aluminium alors qu'au début, elle était plate, il y a eu une augmentation de la surface de la feuille et cette augmentation de surface est permanente puisque les ondulations restent figées. Si elles restent figées, c’est que la limite plastique de l’aluminium a été dépassée. Mais comme la première vibration (c’est-à-dire celle qui s’est propagée le plus loin avant que tout ne se fige) avait forcément une amplitude plus grande lors de sa formation et que son amplitude a diminué lorsque cette ondulation s'est propagée, la limite plastique aurait dû être atteinte dès la première ondulation créée. Or ce n’est pas le cas. Une façon d’expliquer cela serait de dire que la température peut en réalité jouer un rôle, en modifiant la limite plastique de l’aluminium. Il est possible que température plus grande au moment du choc augmente la capacité de l'aluminium à se déformer de façon réversible.
Mais suite à des discussions, nous nous sommes intéressés à une autre hypothèse : est-ce qu’il peut s'agir de flambage ?
2.3 Un phénomène appelé « flambage »
Nous ne connaissions pas ce terme. Il s'avère que notre projet passionne des chercheurs de différentes branches de l'Université de Poitiers et de l'ENSMA. Nous avons alors été mis en relation avec Christophe Coupeau, Professeur des Universités, directeur de l'Ecole doctorale MIMME, spécialisé dans le flambage des films. C'est en observant nos images qu'il a pensé au phénomène possible de flambage pour expliquer nos observations.
Le flambage [3] est un phénomène d'instabilité mécanique qui survient lorsqu'un élément structurel mince et élancé, soumis à une charge de compression, se déforme latéralement de manière soudaine et perpendiculaire à la direction de la charge. On peut voir sur cette vidéo le phénomène de flambage : https://youtu.be/YP_UBNwEoGs?t=296
Ce qui est particulièrement intéressant dans cette vidéo est de constater la régularité des ondulations provoquées par la contrainte appliquée perpendiculairement à la déformation observée.
Alors pourquoi le flambage peut-il aussi être le phénomène à l'origine des ondulations observées dans le cas de la feuille d'aluminium ? Plusieurs raisons :
- On observe des ondulations réparties assez régulièrement, comme dans le cas de la cannette.
- Les amplitudes des ondulations sont plus grandes pour les ondulations les plus éloignées du point d'impact.
Finalement, ce sont les mêmes observations qui nous ont conduits à supposer que le phénomène avait une origine ondulatoire. Mais pourquoi, alors que la vidéo montre des amplitudes qui semblent identiques, pouvons-nous penser à du flambage lors de nos expériences avec le papier d'aluminium alors que dans ce cas-là, les amplitudes des ondulations sont plus faibles lorsqu'on se rapproche du point d'impact ? Ou, autre façon de poser la question, pourquoi, si cela est du flambage, les amplitudes des ondulations doivent-elles être plus faibles lorsqu'on se rapproche du point d'impact ?
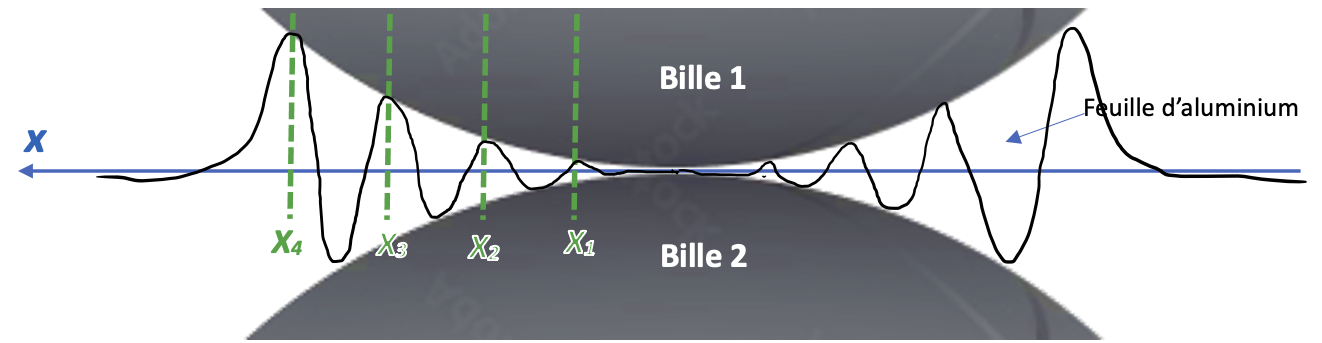
Et bien parce que finalement, les amplitudes des ondulations sont peut-être contraintes par la forme de la bille, comme l'illustre le schéma figure 23.
|
Figure 23. Les amplitudes des ondulations sont-elles imposées par la forme et le rayon des billes ? Source : Geay, Nadaud, Xu, Jarrousse, Bouygues, Fauconnet, Chabasse, Durupt. |
En d'autres termes, les ondulations de l'aluminium auraient pu être de plus grandes amplitudes si la surface de la bille ne les avait pas bloquées selon la direction verticale.
Comment vérifier expérimentalement cette hypothèse ?
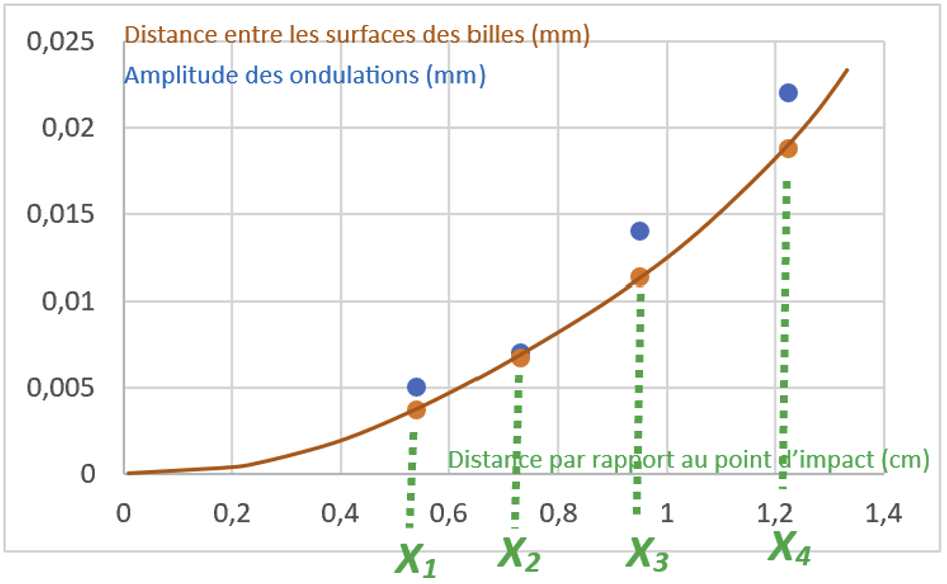
Nous avons tout d'abord voulu savoir si l'évolution des amplitudes des ondulations successives suivait une fonction que l'on pouvait rapprocher de la distance entre les surfaces des billes. Nous avons mené cette réflexion à l'aide des données de la figure 19, en travaillant uniquement sur la partie gauche de la figure, et nous présentons ce que nous obtenons sur la figure 24. En orange, il s'agit de la distance entre les billes, et en bleu, les amplitudes des ondulations successives.
|
Source : Geay, Nadaud, Xu, Jarrousse, Bouygues, Fauconnet, Chabasse, Durupt. |
La comparaison de ces deux évolutions montre effectivement que les amplitudes suivent à peu près la courbure des billes.
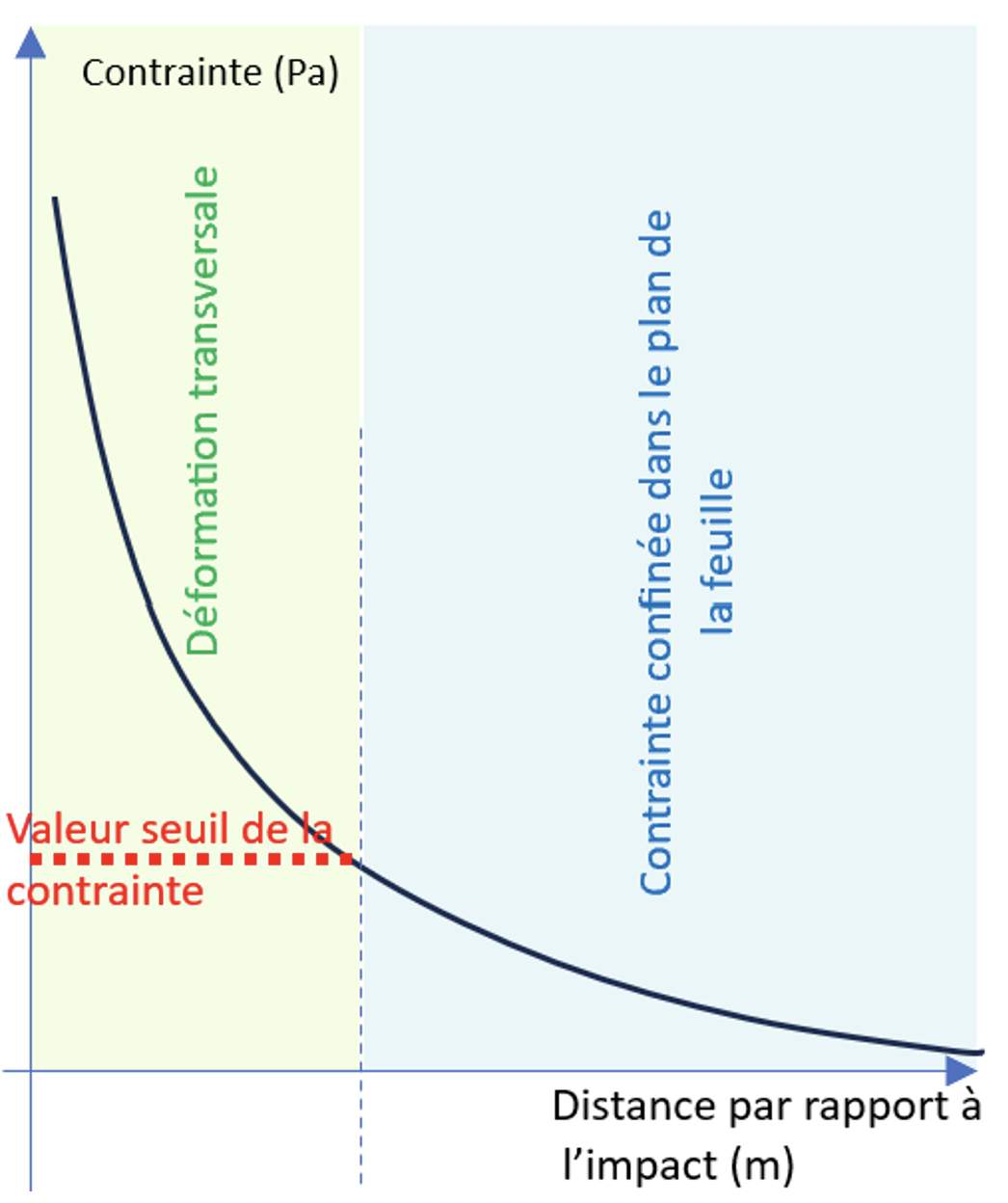
Il y a un autre argument qui permet de supposer que le flambage peut être à l'origine des ondulations observées sur la feuille d'aluminium. En effet, la déformation transversale ne se forme que si la contrainte dans le plan de la feuille dépasse une valeur limite [4]. En dessous de cette valeur, la feuille se comprime sans se déformer transversalement (figure 25). Or, plus on s'éloigne du point d'impact, et plus la contrainte dans le plan de la feuille est de faible amplitude, car la puissance disponible lors de l'impact se répartit sur un cercle de plus en plus grand au fur et à mesure que l'on s'éloigne du point d'impact. À une certaine distance du point d'impact, la contrainte passerait alors en dessous du seuil au-delà duquel la déformation transversale apparaît. Le flambage peut donc expliquer pourquoi les ondulations ne s'observent pas plus loin sur la feuille d'aluminium.
|
Source : Geay, Nadaud, Xu, Jarrousse, Bouygues, Fauconnet, Chabasse, Durupt. |
Ces constats et réflexions nous poussent donc à aller plus loin pour savoir si le flambage est une explication possible du phénomène. Pour cela, nous avons envisagé de tester l'hypothèse du flambage expérimentalement, en faisant des chocs avec des billes de rayons plus petits.
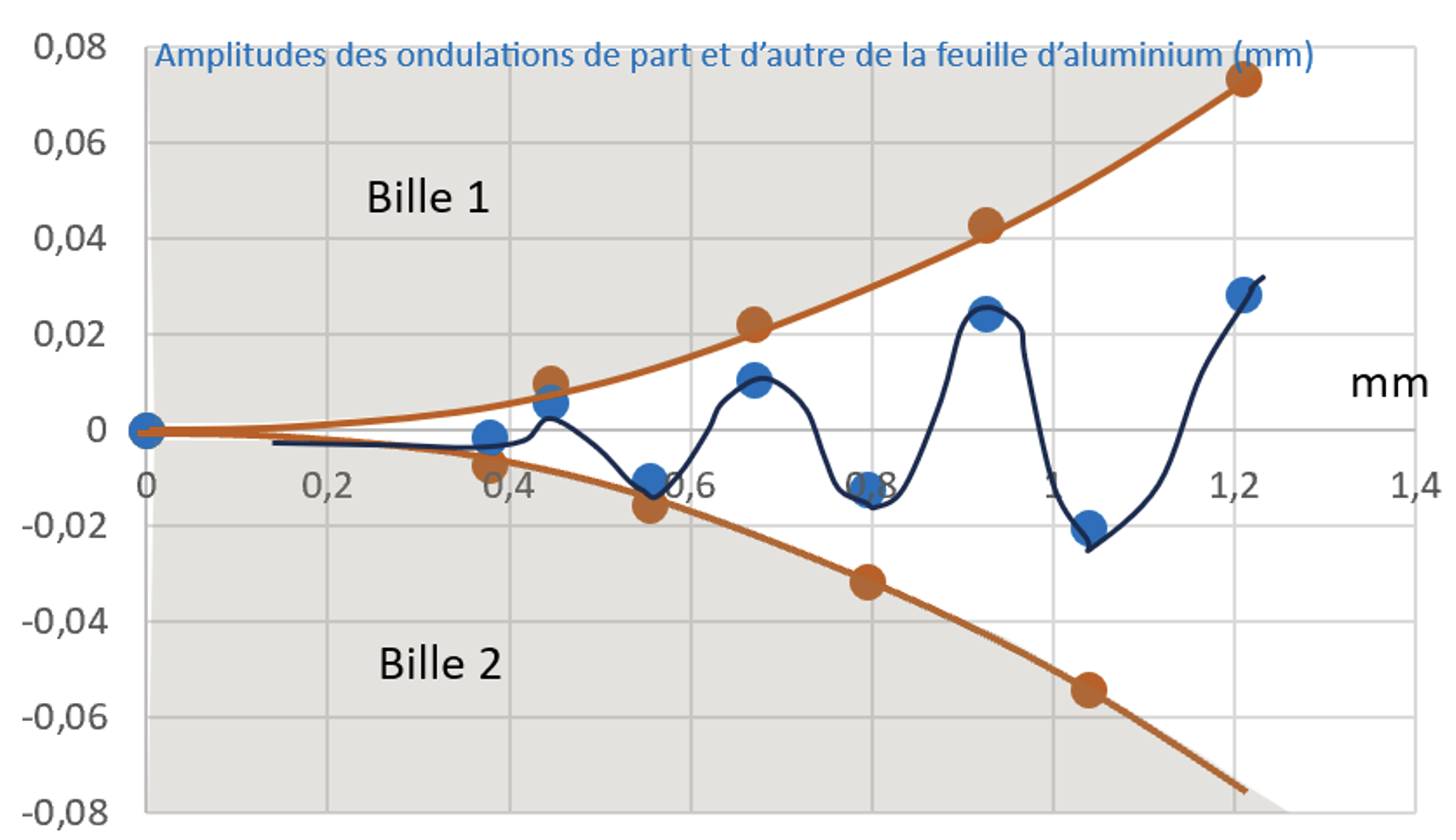
Sur la figure 26, on a représenté l'amplitude des ondulations obtenues (en bleu), comparé à l'espacement entre les billes (en orange) pour des billes de rayon de 1,0 cm.
|
Figure 26. Amplitude des ondulations (en bleu) comparé à la distance entre les deux billes (de rayon de 1,0 cm) Source : Geay, Nadaud, Xu, Jarrousse, Bouygues, Fauconnet, Chabasse, Durupt. |
Les mesures montrent à nouveau que les amplitudes des ondulations semblent contraintes par la courbure des billes. Il est par ailleurs intéressant de voir que, que ce soit les billes de 1 cm ou 2 cm de rayon, le nombre d'ondulations est le même, et l'amplitude et la position de la dernière ondulation sont très voisines.
Finalement, l'hypothèse du flambage semble prendre le dessus pour expliquer la formation des ondulations. Une question se pose tout de même :
Dans le cas du flambage, la contrainte est exercée à l'extrémité d'un système, mais l'autre extrémité est disposée contre un support qui la retient. Ce n'est pas le cas de la feuille d'aluminium, dont les extrémités sont complètement libres. Alors pourquoi observerait-on un ensemble d'oscillations ? À l'heure où l'on écrit le mémoire, nous ne savons pas. Mais nous avons des hypothèses. Par exemple, est-ce que le fait que le choc soit très rapide (de l'ordre de 100 µs) fait que le matériau situé à quelques millimètres du point d'impact se comporte comme un objet fixé qui maintiendrait alors la partie de l'aluminium affectée par le choc ? Nous avons prévu de faire une nouvelle expérience au cours de laquelle nous allons comprimer la feuille d'aluminium, toujours avec les billes d'acier, mais cette fois-ci très progressivement, dans une presse performante. Nous avons hâte de réaliser cette expérience.
D'autre part, nous avons évoqué le fait que la feuille d'aluminium extérieure à la zone affectée par les ondulations était forcément attirée vers la zone d'impact. Nous nous posons alors la question de savoir ce qui se passerait si l'on diminuait drastiquement la surface du papier d'aluminium utilisée lors de l'expérience.
Conclusion
C'est impressionnant de voir à quel point une expérience si simple peut conduire à tant d'interrogations. Pour y répondre, nous avons suivi différentes pistes. Les expériences réalisées permettent de trouver des arguments en faveur aussi bien d'une onde que du flambage. Nous avons déjà fait les démarches pour réaliser de nouvelles expériences qui nous permettront probablement de trouver laquelle de ces explications possibles est correcte (contrainte à appliquer lentement sur l'aluminium, modifier le rayon des billes, modifier la taille de la feuille utilisée,…). Nous avons également commencé à monter un nouveau support pour la feuille d'aluminium pour filmer avec une caméra rapide à 20 000 images par seconde la tranche de l'aluminium. Nous aurions voulu filmer le point d'impact pour voir si une onde se propage ou si les ondulations apparaissent sans propagation d'une onde, mais les billes cachent la zone de l'impact au moment du choc. En attendant, le fait de se lancer dans un sujet sans connaître la réponse, mais en essayant d'être le plus rigoureux possible dans notre démarche d'investigation, nous permet de comprendre pourquoi les chercheurs que nous avons rencontrés sont si passionnés par leur métier. Nous continuerons de travailler avec eux : Romain Bellanger, ingénieur d'études à l'institut Pprime, Florian Moreau, chercheur à l'institut Pprime, Frédéric Pailloux, chercheur au SP2MI, Thibault de Résseguier, directeur de recherche à l'ENSMA, Christophe Coupeau, professeur des universités.
Bibliographie
[1] Smashing Sphere Demo, Educational Innovations.
[2] Dureté des boules de pétanque, Jean-Michel Courty et Édouard Kierlik, Pour la science n°381, 2009.
[3] Définition du flambage, Wikipedia, consulté en 2025.
[4] Influence du substrat sur le phénomène de cloquage, Thèse de Frédéric Foucher, Université de Poitiers, HAL, 2007.
Pour citer cet article :
Comment expliquer la formation des ondulations sur une feuille d'aluminium, autour d'un point d'impact de deux boules d'acier venant percuter lafeuille en sandwich?, Geay, Nadaud, Xu, Jarrousse, Bouygues, Fauconnet, Chabasse, Durupt, février 2026. CultureSciences Physique - ISSN 2554-876X, https://culturesciencesphysique.ens-lyon.fr/ressource/Boules-alu-Olympiades.xml