Activer le mode zen
Ressource au format PDF
Mots-clés
- physique du sport
- vitesse
- frottement
- roulement
- trajectoire
Classification
Quelle rotation peut être acquise par une balle de tennis de table qui arrive obliquement sur une table, sans rotation initiale ?
30/09/2024
Table des matières
Introduction
Au tennis de table, une meilleure compréhension de l'interaction entre la balle et la surface de jeu peut s'avérer essentielle pour les joueurs, notamment en ce qui concerne la vitesse de rotation qu'elle peut atteindre. Cela aura un impact sur la manière dont les joueurs contrôlent la balle et donc influence directement leur façon de jouer.
Dans cet article, nous allons nous intéresser au comportement dynamique d'une sphère creuse (la balle de tennis de table) au contact d'une surface rigide (la table de tennis de table). En particulier, nous allons regarder si nous pouvons prédire la vitesse de rotation en sortie de rebond.
1. Contexte
Dans la perspective des Jeux Olympiques et Paralympiques que la France accueille en 2024, une partie de la communauté scientifique française s'est intéressée à la recherche autour du sport. Dans ce contexte, un programme de recherche nommé « Sciences 2024 » a été initié réunissant 11 grandes écoles ainsi que le CNRS pour accompagner les athlètes français dans leurs quêtes de médailles.
Habituellement, les athlètes progressent de manière empirique en accumulant entraînements, expériences et confrontations répétées avec les meilleurs de la discipline, ce qui peut suffire à atteindre un niveau d'excellence. Cependant, lorsqu'il s'agit de repousser les limites de la performance, quel que soit le sport, il devient nécessaire d'adopter une démarche scientifique pour décortiquer tous les facteurs d'amélioration.
La physique est la science qui consiste à observer et à comprendre les phénomènes qui nous entourent et cherche à les expliquer par des lois générales. Par exemple, la trajectoire d'une balle ou les mécanismes qui régissent les mouvements peuvent être mieux compris et du matériel plus efficace ou plus adapté peut alors être développé en fonction du critère à optimiser. La physique expérimentale met à disposition divers instruments de mesure permettant de quantifier les sensations des sportifs. Nous pouvons caractériser des intuitions, mesurer des propriétés non accessibles autrement.
2. Dispositif expérimental de caractérisation du rebond de la balle
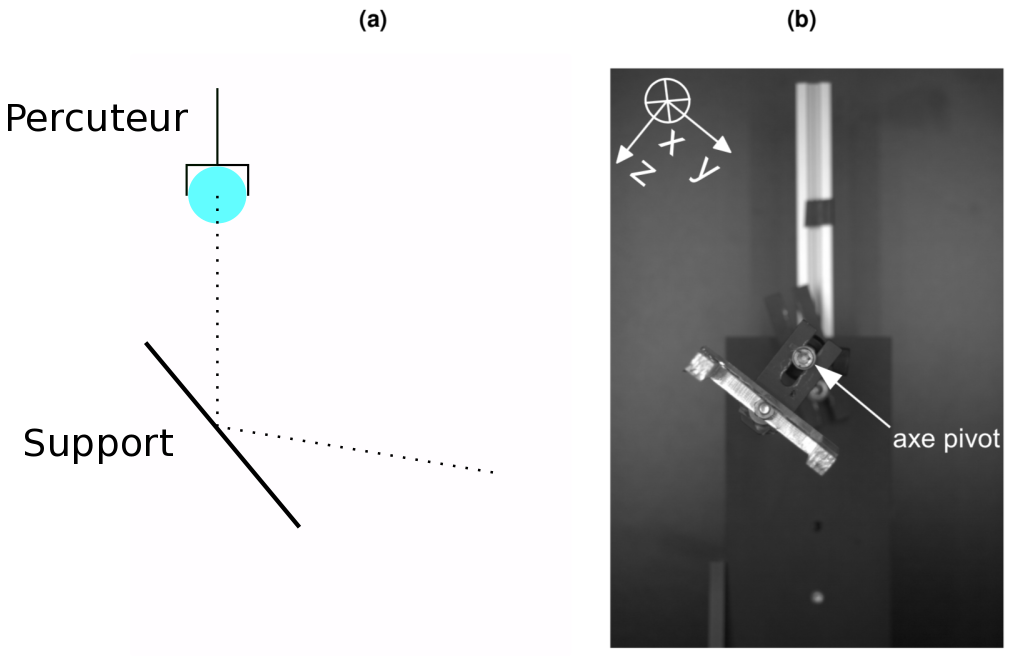
Nous avons conçu un dispositif expérimental, au sein du laboratoire, pour étudier l'interaction de la balle de tennis de table avec une surface (représentant la table de tennis de table), dans un régime dynamique qui se rapproche des conditions de jeu, figure 1.
La balle est mise en mouvement au moyen d'un percuteur mécanique. Elle est lancée à la verticale sur le support et le rebond est filmé avec une caméra rapide. L'impact se fait dans une boîte fermée afin d'assurer la sécurité du manipulateur. Des barres de LEDs puissantes sont placées face au rebond afin d'obtenir un bon contraste sur l'image de la balle (blanche) sur le fond noir de la boîte.
Le support a été choisi transparent en verre, pour d'autres études plus poussées sur le flambage de la balle [1] (études qui ne seront pas présentées dans cet article). La structure qui maintient le support est reliée à une liaison pivot fixée, permettant d'imposer un angle d'incidence.
Figure 1. Schéma et photo du dispositif de mesure du rebond de la balle (a) Schéma du dispositif. (b) Image capturée depuis la caméra, de face. L'axe de la liaison est situé en plein centre de l'image. Source : Théophile Rémond [1]. |
En effet, lors d'un match de tennis de table, la balle arrive rarement dans une direction normale à la raquette. Les joueurs vont constamment incliner leur raquette pour essayer d'accélérer la balle vers l'avant lors d'un coup offensif ou la freiner lors d'un coup défensif. La balle a donc, dans la plupart des cas, également une forte vitesse de rotation qui influencera la manière dont ils la contrôleront et s'y adapteront. Si la balle tourne peu au service par exemple, l'adversaire pourra plus facilement terminer le point. Pareillement, la balle n'arrive jamais normale à la table. Par exemple, si l'on considère que le joueur frappe la balle à une hauteur de 1 m au-dessus de la table, afin de renvoyer la balle sur la table 2 m plus loin, l'angle entre la trajectoire de la balle et la table est d'environ 26°.
Afin de rester dans une situation simple et rapide à mettre en place, nous n'imposerons pas de rotation incidente à la balle. Le problème pourra ainsi être appréhendé plus facilement, avec l'objectif de généraliser, dans un second temps, à un modèle de rebond sur surface rigide.
3. Choix des paramètres et mesures expériementales
3.1 Conditions initiales
Comme nous l'avons évoqué, cette configuration est simple à mettre en place, il suffit d'incliner la surface d'étude sur le précédent dispositif expérimental présenté en figure 1. Cela a l'avantage d'être une configuration simple dans l'objectif de mieux appréhender le problème et nous pouvons aussi effectuer des mesures très précises et répétables sur ce dispositif. La balle arrive donc verticalement sur la surface solide inclinée d'un angle. Nous avons effectué des rebonds en faisant varier \(\theta_i \) entre 0° et 60° et des vitesses incidentes de la balle \(v_i \) entre 2 m.s-1 et 13 m.s-1.
3.2 Mesures
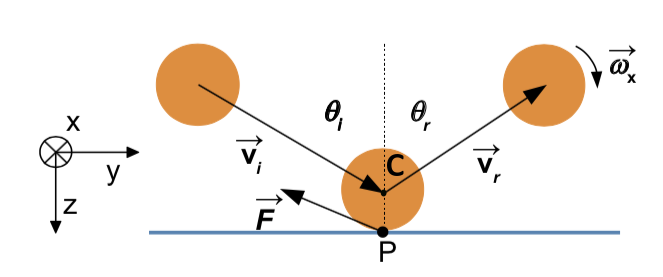
La balle atteint la surface solide avec la vitesse incidente \(\overrightarrow{v_i} \) formant un angle \(\theta_i \) avec la normale à la surface, figure 2. Sous l'effet de la force de contact \(\overrightarrow{F} \) pendant la collision, la balle commence à tourner. Elle quitte la surface avec la vitesse réfléchie \(\overrightarrow{v_r} \) et tourne avec la vitesse angulaire \(\overrightarrow{\omega_{x}} \) autour de l'axe \(\overrightarrow{x} \). Nous notons \(\theta_r \) l'angle réfléchi entre la normale à la surface et la vitesse \(\overrightarrow{v_r} \). En faisant ce choix, nous avons \(\theta_r = \theta_i \) si la balle rebondit symétriquement par rapport à la normale à la surface.
Figure 2. Schéma du rebond d'une sphère sur une surface solide indéformable La balle atteint la surface solide avec la vitesse incidente \(\overrightarrow{v_i} \) formant un angle \(\theta_i \) avec la normale à la surface (et sans rotation initiale). Après le rebond, sous l'action de la force de contact \(\overrightarrow{F} \) pendant la collision, la balle est mise en rotation à la vitesse angulaire \(\overrightarrow{\omega_{x}} \) et la vitesse réfléchie \(\overrightarrow{v_r} \) de la balle forme un angle \(\theta_r \) avec la normale à la surface. Source : Théophile Rémond. |
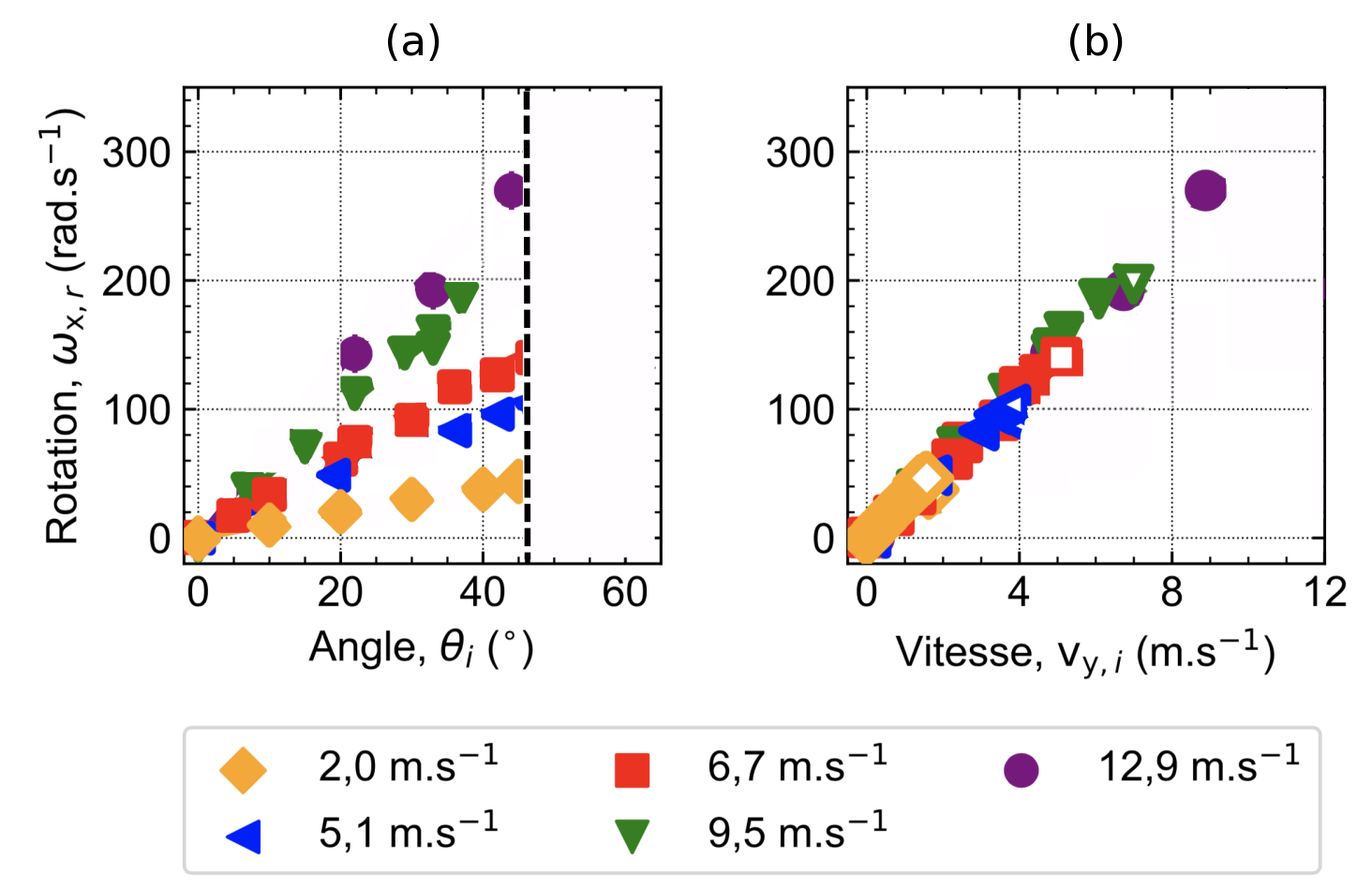
Nous reportons sur la figure 3a, l'évolution de la vitesse angulaire \(\omega_{x} \) en fonction de l'angle d'incidence \(\theta_i \) pour différentes vitesses incidentes \(v_i \) (marqueurs de couleur). Dans un premier temps, on se limite à un angle d'incidence maximal de 45°. Nous observons qualitativement que \(\omega_{x} \) augmente à partir de zéro avec l'angle d'incidence \(\theta_i \). Rappelons que \(\theta_i =\) 0° correspond à l'incidence normale, et donc la rotation de la balle reste nulle. Il est particulièrement intéressant de noter sur la figure 3b qu'en dessous de 45° et pour toutes les vitesses incidentes couvertes, \(\omega_{x} \) est simplement proportionnelle à la vitesse tangentielle incidente \(v_{y,i} = v_i \sin \big(\theta_i\big) \).
En (a), on observe que \(\omega_{x} \) augmente avec \(\theta_i \), En (b), on observe que \(\omega_{x} \) est simplement proportionnel à \(v_{y,i}\), quelle que soit la norme de la vitesse incidente \(v_{i}\). Source : Théophile Rémond [1]. |
4. Résolution analytique
Nous avons observé expérimentalement que pour des angles d'incidence inférieurs à 45°, la vitesse de rotation après rebond, \(\omega_{x} \), est proportionnelle à la composante tangentielle de la vitesse incidente \(v_{y,i}\), indépendamment de la valeur de la vitesse incidente \(v_{i}\). Nous proposons un modèle mécanique basé sur des hypothèses très simples pour expliquer complètement le comportement de la balle.
On peut considérer, par souci de simplicité, qu'une coque sphérique entre en contact avec un support solide et qu'aucun des solides ne se déforme lors de la collision. Le substrat exerce donc une force \(\overrightarrow{F}\) sur la balle en un unique point de contact P, figure 4.
Également, la balle sphérique gardant sa rotation autour d'un axe de symétrie \(\Delta\), son moment cinétique, \(\overrightarrow{\sigma}\), peut donc s'exprimer comme le produit de son moment d'inertie \(I_{\Delta}\) et de sa vitesse angulaire \(\overrightarrow{\omega} \),
$$ \overrightarrow{\sigma} = I_{\Delta} \overrightarrow{\omega} $$
En particulier, dans le cas d'une sphère creuse de rayon \(R\) et de masse \(m\), son moment d'inertie s'écrit : \( I_{\Delta} =\frac{2}{3} m R^2 \).
D'après le théorème du moment cinétique, la force \(\overrightarrow{F}\) exerçant un moment sur la balle, nous pouvons écrire pendant la durée du contact \(\tau\),
$$ I_{\Delta} (\overrightarrow{\omega_r} - \overrightarrow{\omega_i} ) = \int_{0}^{\tau} (\overrightarrow{CP} \wedge \overrightarrow{F}) ~ dt $$
où C correspond au centre de la balle et P le point de contact.
La balle atteint la surface solide avec la vitesse incidente \(\overrightarrow{v_i} \) formant un angle \(\theta_i \) avec la normale à la surface (et sans rotation initiale). Après le rebond, sous l'action de la force de contact \(\overrightarrow{F} \) pendant la collision, la balle est mise en rotation à la vitesse angulaire \(\overrightarrow{\omega_{x}} \) et la vitesse réfléchie \(\overrightarrow{v_r} \) de la balle forme un angle \(\theta_r \) avec la normale à la surface. Source : Théophile Rémond. |
L'origine du temps est prise afin de coïncider avec le début du contact. Nous rappelons ici que la vitesse angulaire incidente est nulle. Ainsi, d'après le théorème de la quantité de mouvement, en dénotant \(\overrightarrow{v_{i}}\) et \(\overrightarrow{v_{r}}\), les vitesses respectivement avant et après le rebond, on peut écrire en négligeant l'accélération due à la gravité :
$$ m ~(\overrightarrow{v_r} - \overrightarrow{v_i} ) = \int_{0}^{\tau} \overrightarrow{F} dt $$
Par ailleurs, en notant que \( \overrightarrow{CP} = R \overrightarrow{z} \) est perpendiculaire à la surface du solide, nous pouvons écrire \( \overrightarrow{CP} \wedge \overrightarrow{F} = -(RF_y) \overrightarrow{x} \), où \(F_y\) est la composante tangentielle de la force \(\overrightarrow{F}\).
L'équation peut alors être réécrite en projection le long de l'axe \(\overrightarrow{x}\), et dans notre configuration :
$$ I_{\Delta} \omega_x = -R \int_{0}^{\tau} F_y ~dt $$
En combinant ces deux dernières équations, en projection le long de l'axe \(\overrightarrow{y}\) :
$$ m ~(v_{y,r} - v_{y,i} ) = \int_{0}^{\tau} F_y ~dt = - \frac{I_{\Delta} \omega_x}{R} ~~~~~~~~\color{blue}{(eq A)} $$
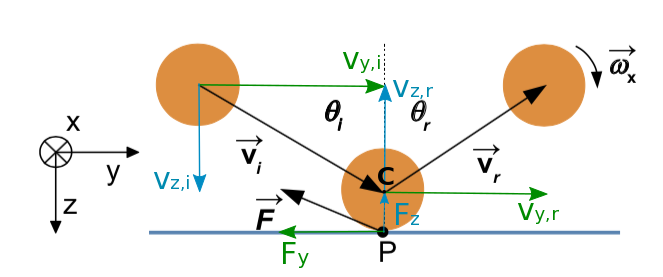
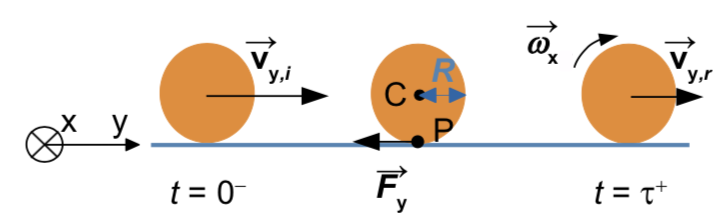
Cette équation projetée selon \(\overrightarrow{y}\) est illustrée par la figure 5. La balle arrive avec la vitesse \(v_{y,i}\) (et sans vitesse de rotation initiale). Lors du contact, une force \(\overrightarrow{F_y}\) s'applique au point de contact \(P\) à un rayon \(R\) du centre de la balle, une force qui va freiner le mouvement tangentiel et exercer un moment de rotation. La balle quitte donc la surface au temps \(\tau\) avec une vitesse réduite \(v_{y,r}\) et une vitesse de rotation \(\omega_x\).
Pendant le contact, la balle va donc initialement glisser et \(\overrightarrow{F_y}\) est une force de friction qui s'oppose à son mouvement.
Figure 5. Schéma de la configuration considérée pour le rebond de la balle La balle arrive avec une vitesse tangentielle \(\overrightarrow{v_{y,i}}\) sans rotation initiale sur une surface rigide. Une force de friction \(\overrightarrow{F_{y}}\) s'applique sur la balle au point de contact, ce qui va la freiner linéairement et exercer un moment de rotation à la balle. Source : Théophile Rémond [1]. |
4.1 Cas où la balle glisse et n'atteint pas le roulement
Pour une vitesse d'incidence donnée, une augmentation de l'angle d'incidence \( \theta_i \) provoque simultanément l'augmentation de la vitesse tangentielle \( v_{y,i} \) et la diminution de la vitesse normale. En conséquence, si par exemple la composante tangentielle (\( F_y \)) de la force \(\overrightarrow{F}\) est due au frottement solide, elle est directement proportionnelle à la force normale et elle sera de moins en moins capable de freiner la vitesse tangentielle de la balle et donc d'arrêter le glissement initial du contact.
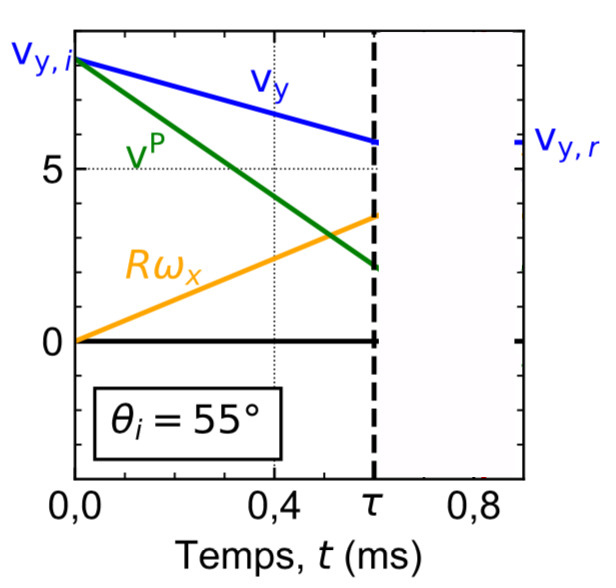
C'est ce qui est représenté sur la figure 6, en augmentant l'angle d'incidence \( \theta_i \), nous augmentons également \( v_{y,i} \), tout en baissant la force normale, \( F_{z} \), se traduisant par une décroissance de \( v_{y} \) (pente bleue).
Source : Théophile Rémond [1]. | Source : Théophile Rémond. |
Ainsi, en supposant un temps de contact \( \tau \) indépendant des conditions initiales de la balle, nous pouvons penser qu'il y aura une transition entre deux régimes où le système ne sera plus capable d'assurer les conditions de roulement sans glissement. Autrement dit, la balle quitte la surface au temps \( \tau \) en glissant encore. La vitesse du point de contact s'écrit \(v^P = v_y - R \omega_x \).
D'une part, afin de rendre compte de la transition, certes de manière simpliste, nous considérons que la composante tangentielle de la force, \( F_y \), est due à la friction et nous écrivons simplement \( F_y = - \mu \vert F_z \vert \) (à condition que \( v_y > 0 \)), où \( \mu \) est le coefficient de friction entre la surface solide et la balle.
D'autre part, en considérant la dynamique le long de la normale au support du rebond, à tout moment il y a, \( F_z = m \frac{d v_z}{dt} \).
D'où, en considérant la dynamique dans le plan du support, on a \( m \frac{d v_y}{dt} = - \mu \vert F_z \vert \), tel que, intégré dans le temps :
$$ v_{y,r} ~- v_{y,i} = \mu ~(v_{z,r} ~- v_{z,i}) ~~~~~~~\color{blue}{(eq B)} $$
En effet, à partir du seuil de glissement, la force tangentielle ne s'annule plus avant le temps de contact et donc nous avons bien la relation \( F_y = - \mu \vert F_z \vert \) vraie sur tout le temps de contact \( \tau \), ce qui nous permet d'intégrer. De plus, d'après l'équation (eq A), nous avons \( R \omega_x = - \frac{3}{2} (v_{y,r} - v_{y,i}) \). En combinant avec l'équation (eq B), nous arrivons finalement à la relation, dans le cas où la balle glisse pendant tout le contact :
$$ - \frac{2}{3} ~R \omega_x = \mu ~\big( v_{z,r} - v_{z,i} \big) $$
En désignant par \( \epsilon_z \) la restitution de vitesse le long de la normale à la surface, \( \epsilon_z = \) \( v_{z,r}\) / \(v_{z,i} \), on obtient :
$$ R \omega_x = \frac{3}{2} \mu ~\big( 1 + \epsilon_z \big) ~ v_{z,i} $$
Cette relation nous indique que lorsque la balle glisse en sortie de rebond, la vitesse de rotation \( \omega_x \) baisse avec la vitesse tangentielle de la balle \( v_{z,i} \) ou encore l'angle d'incidence \( \theta_i \).
En effet, la vitesse normale s'écrit : \( v_{z,i} = \sqrt{v_i^2 - v_{y,i}^2} = v_i \sqrt{1- \sin^2(\theta_i)}\)
4.2 Cas où la balle atteint le roulement
Supposons maintenant que la balle arrête de glisser et se met à rouler en quittant la surface. Dans ce cas, la vitesse du point de contact \(P\) devient nulle (plus de glissement) et la friction s’exerçant au point \(P\), \(\overrightarrow{F_y}\), s’annule aussi.
La vitesse du point de contact est \(v^P = v_y - R \omega_x \) et donc la balle roule en sortie de rebond si \( R \omega_x = v_{y,r} \).
Cela est possible si la force \(\overrightarrow{F_y}\) est suffisante pour donner assez de rotation \(\omega_x\) tout en baissant \( v_{y,r} \), et donc que la force normale \(\overrightarrow{F_z}\) soit assez élevée (angle de rebond faible).
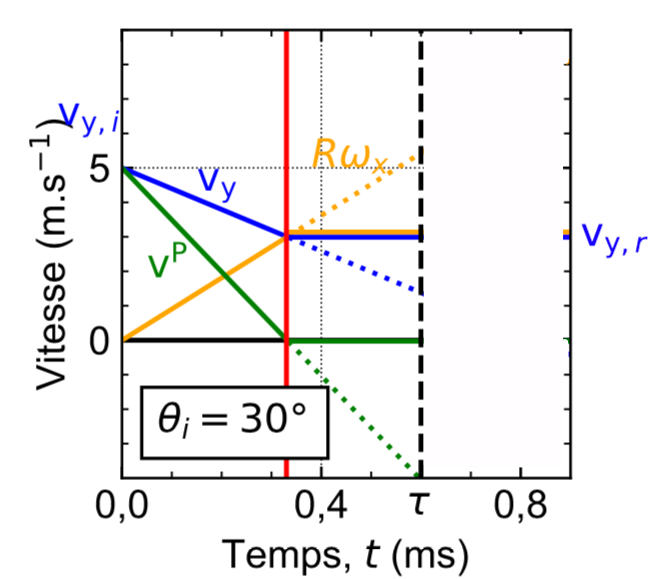
C'est ce qui est représenté sur la figure 8 où la force freine la vitesse \( v_{y} \) tout en augmentant \( R \omega_x \), et lorsque les deux valeurs s'égalisent ( \(v^P =0 \), annoté sur la figure par une ligne rouge), la balle commence à rouler avec plus aucune force tangentielle \(\overrightarrow{F_y}\) agissant sur elle.
Source : Théophile Rémond [1]. | Source : Théophile Rémond. |
En injectant la condition de roulement \( R \omega_x = v_{y,r} \) dans l'équation (eq A), et avec la valeur du moment d'inertie \(I_\Delta\) pour une coque sphérique (\(I_\Delta = \) 2/3 \( m R^2 \) ), on obtient :
$$ m ~R \omega_x - m ~v_{y,i} = - \frac{2}{3} \frac{m R^2}{R} \omega_x $$
D'où :
$$ R \omega_x = \frac{3}{5} v_{y,i} $$
La vitesse angulaire réfléchie est ici proportionnelle à la composante tangentielle de la vitesse incidente \( v_{y,i} \), indépendamment de la valeur de la vitesse incidente \( v_{i} \), dans le cas où l'hypothèse d'une balle en roulement sans glissement est vérifiée. La relation ne dépend d'aucune propriété de contact entre la balle et la surface.
Pour aller plus loin, nous remarquons que \( v_{y,r} =\frac{3}{5} v_{y,i} \) permet l'estimation de l'angle de réflexion \( \theta_r \). En effet, \( \tan\big(\theta_r \big) =\) \(v_{y,r}\) / \(v_{z,r} \).
Avec \( \epsilon_z \) la restitution de vitesse le long de la normale à la surface, \( \epsilon_z = \) \( v_{z,r}\) / \(v_{z,i} \), on obtient :
$$ \tan \big( \theta_r \big) = \frac{3}{5 \epsilon_z} \tan \big( \theta_i \big) $$
En supposant que les pertes de vitesse selon la normale \(z\) sont limitées (surface rigide) et que \( \epsilon_z \) est supérieure à 3/5, cette relation nous montre que la balle se cabre lors de son rebond, \( \theta_r \) est inférieur à \( \theta_i \).
Maintenant, nous pouvons nous pencher sur la valeur du seuil entre les régimes de glissement et roulement, et s'interroger sur la valeur de l'angle critique à partir duquel la balle glisse totalement.
Reprenons l'illustration figure 8 sur laquelle la ligne verticale rouge représente le moment auquel la balle commence à rouler et donc la force tangentielle \( F_y \) s'annule. Pour des grands angles d'incidence, lorsque la balle va glisser pendant tout le temps de contact, cette ligne est située après le temps \( \tau \). La force tangentielle s'annulera donc lors de la séparation de la balle et la surface, au temps \( \tau \), en même temps que la force normale. L'angle critique correspond à l'angle où cette ligne rouge est confondue avec \( \tau \).
En tenant compte que la condition de roulement est toujours valable au seuil et impose donc \( v_{y,r} = - \frac{3}{5} v_{y,i} \), et avec l'angle d'incidence \( \theta_i \) (\( v_{z,i} = v_i \cos (\theta_i) \) et \( v_{y,i} = v_i \sin (\theta_i) \)), nous obtenons à partir de l'équation (eq B) l'angle critique \( \theta_i^c \) sous la forme :
$$ \tan \big( \theta_i^c \big) = 5 \frac{1 + \epsilon_z}{2} \mu $$
Cet angle d'incidence critique est régi par le temps de collision (que l'on peut considérer constant) et le frottement entre la balle et le support du rebond.
Enfin, pour aller plus loin, ayant accès à toute la cinématique de la balle, de façon analogue nous pouvons remonter à la valeur de l'angle de rebond \( \theta_r \). On a :
$$ \tan \big( \theta_r \big) = \frac{1}{\epsilon_z} \tan \big( \theta_i \big) - \mu \frac{1 + \epsilon_z}{\epsilon_z} $$
4.3 Comparaison avec les données expérimentales
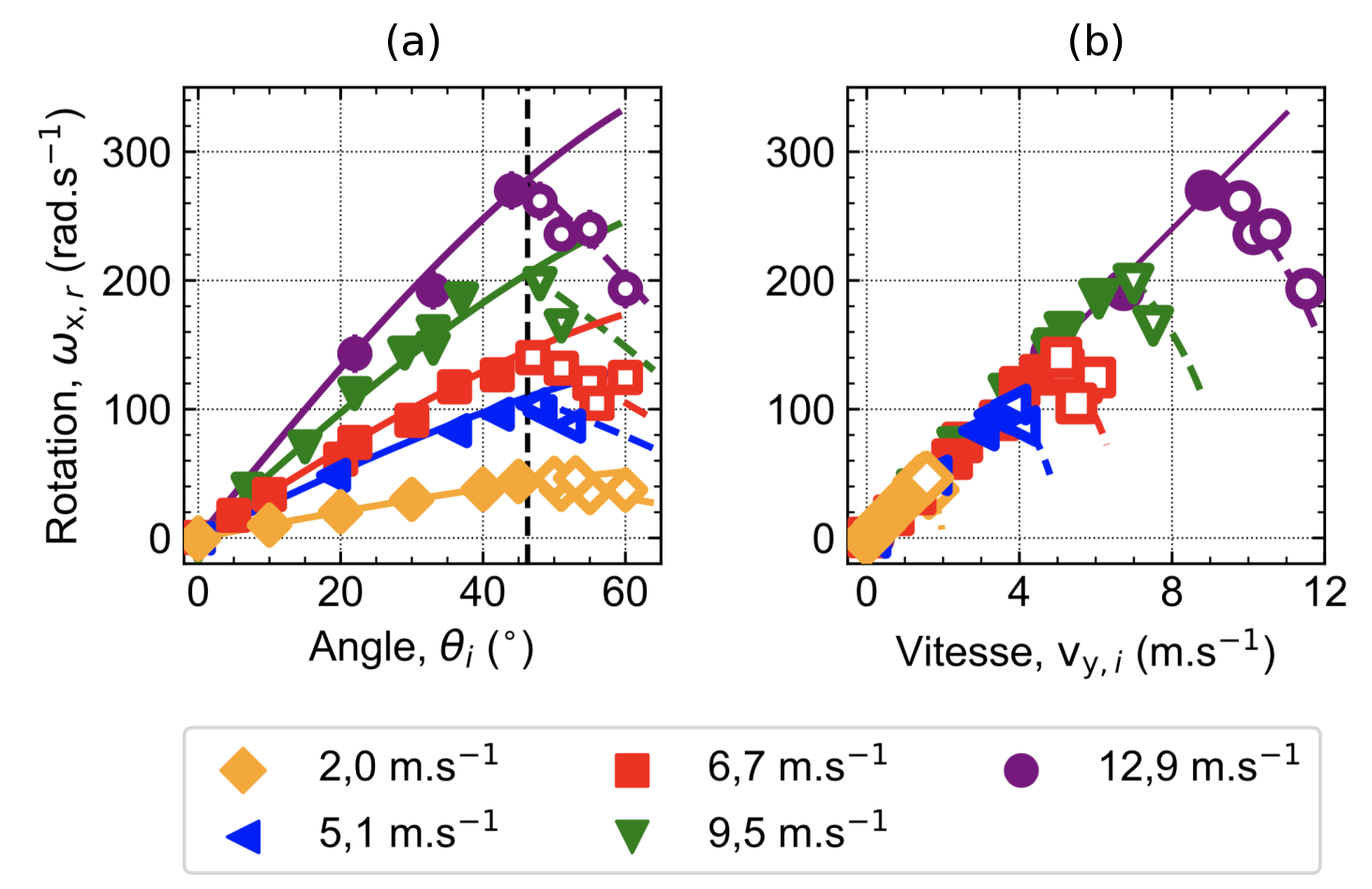
Nous reportons sur la figure 10a, par dessus les données expérimentales (marqueurs), l’évolution de la vitesse angulaire \( \omega_x \) en fonction de l’angle d’incidence \( \theta_i \) pour différentes vitesses incidentes \( v_i \), calculée à l'aide de notre modèle, en lignes pleines et lignes pointillées.
En (a), on observe les deux régimes : en dessous de typiquement 45°, \(\omega_{x} \) augmente avec \(\theta_i \), et au-delà, la vitesse angulaire \(\omega_{x} \) chute. En (b), on observe qu'en dessous de la transition, \(\omega_{x} \) est simplement proportionnel à \(v_{y,i}\), quelle que soit la norme de la vitesse incidente \(v_{i}\). Source : Théophile Rémond [1]. |
Les lignes pleines sont la prédiction de l’équation :
$$ R \omega_x = \frac{3}{5} v_{y,i} ~~~~~~~~ \color{blue}{(eq C)}$$
qui suppose que la coque sphérique roule sans glisser lorsqu’elle quitte le support du rebond.
Le modèle théorique s’avère parfaitement prédire les données expérimentales. Ainsi, on en conclut que pour des angles modérés, la balle roule parfaitement en quittant le support. Le résultat le plus frappant obtenu à partir de cette modélisation simple, est que la relation ne dépend d’aucun paramètre expérimental, à l’exception du fait que la balle est une coque sphérique à paroi mince, ce qui détermine la valeur du moment d’inertie \(I_\Delta\) et donc la constante 3/5 dans l’équation (eq C).
À partir de la valeur expérimentale de \(\theta_i^c \approx\) 45°, en tenant compte du fait que \(\epsilon_z\) est bien constant et proche de 1 (mesures présentées en [1]), nous obtenons une première estimation du coefficient de friction, \(\mu \approx\) 0,2.
Les lignes pointillées sont la prédiction de l’équation :
$$ R \omega_x = \frac{3}{2} \mu ~\big( 1 + \epsilon_z \big) ~ v_{z,i} $$
qui suppose que la coque sphérique est toujours dans une phase de glissement lorsqu’elle quitte le support du rebond (\(\epsilon_{z} = \) 0, 9 et \(\mu = \) 0,22).
Dans ce régime de glissement, toute la cinématique de la balle est bien décrite par le modèle analytique aux hypothèses trés simples, développé ci-dessus. Nous montrons même que ce dernier est généralisable à d’autres conditions de contact, en utilisant d’autres balles par exemple, toujours sur surface solide. Une loi de choc complète, en trois dimensions, incluant des vitesses de rotation incidentes, a pu être développée afin de prédire le rebond d’une balle de tennis de table sur surface rigide [1].
Conclusion
Cette étude a considéré le rebond d'une balle de tennis de table en incidence oblique sans rotation initiale. En considérant un modèle mécanique simple basé sur une balle indéformable, nous arrivons à prédire toute la cinématique de la balle en sortie du rebond. Pour des angles d'incidence modérés, la balle quitte le support de rebond en roulant sans glisser. Tout est bien décrit sans connaissance des propriétés du matériau du support de rebond. Au-delà d'un angle d'incidence critique, qui est gouverné par le temps de collision constant et le frottement entre la balle et le substrat, le point de contact ne fait que glisser. Dans ce cas, les vitesses de translation et angulaire après rebond peuvent être prédites à condition de connaître le coefficient de friction \( \mu \). Le modèle présenté est solide et s'accorde parfaitement avec les résultats expérimentaux dans le cas d'une balle de tennis de table standard qui impacte une plaque de verre.
De plus, ce modèle est facilement transposable au cas où la balle possède une rotation initiale. Pour cet aspect, on pourra se repporter aux travaux de thèse dont cet article est issu [1].
Références
[1] Physique du rebond : Application à la balle de tennis de table, Thèse de doctorat de Théophile Rémond, 2023, ENS de Lyon.
Pour citer cet article :
Quelle rotation peut être acquise par une balle de tennis de table qui arrive obliquement sur une table, sans rotation initiale ?, Rémond, septembre 2024. CultureSciences Physique - ISSN 2554-876X, https://culturesciencesphysique.ens-lyon.fr/ressource/rebond-tennis-de-table.xml