Activer le mode zen
Ressource au format PDF
Mots-clés
Classification
Quelle est la hauteur maximale à laquelle un hélicoptère de secourisme peut voler ?
15/09/2025
Résumé
Une résolution de problème pour proposer "à main levée" une estimation de la hauteur maximale de vol d'un hélicoptère.
Table des matières
Lors de notre année de Licence 3 en Sciences de la matière à l'ENS de Lyon, dans le cadre de notre cursus nous avons pu participer au module « Résolution de problème ». Nous avons choisi ce problème que nous vous soumettons dans cet article.
1. Position du problème
Voici le problème et l'affiche correspondante :
2. Résolution
Attention - Nous indiquons ici, que l'intérêt de l'exercice repose sur une estimation des ordres de grandeurs. Nous ne cherchons pas à réaliser une analyse fine de la question. L'idée est qu'à l'aide des connaissances en physique, on soit capable de déterminer « à main levée » une estimation de la hauteur maximale de vol d'un hélicoptère.
On cherche l'altitude maximale à laquelle un hélicoptère peut voler. Le vol d'un hélicoptère est dû la force de portance qui s'exerce sur ses pales, qui rencontrent un vent relatif du fait de leur rotation dans l'air. Pour que son altitude augmente, il faut que cette force de portance soit supérieure en norme au poids de l'hélicoptère. Or, à mesure que l'on monte, l'air voit sa masse volumique diminuer, et la force de portance avec elle. On cherche donc à quelle altitude la force de portance est tout juste égale au poids de l'hélicoptère.
Ce problème demande donc de calculer la norme de la force de portance qui s'exerce sur les pales de l'hélicoptère, et d'être capable de décrire l'évolution de la masse volumique de l'air en fonction de l'altitude.
2.1 Hypothèses
Pour résoudre ce problème, nous ferons différentes hypothèses :
- L'atmosphère est supposée isotherme ;
- L'air est assimilé à un gaz parfait ;
- L'accélération de pesanteur est supposée constante en fonction de l'altitude ;
- Les seules forces que subit l'hélicoptère sont son propre poids et la force de portance de l'air sur les pales (\(F_Z\)). Nous éliminons donc tous les frottements, d'éventuels vents latéraux ;
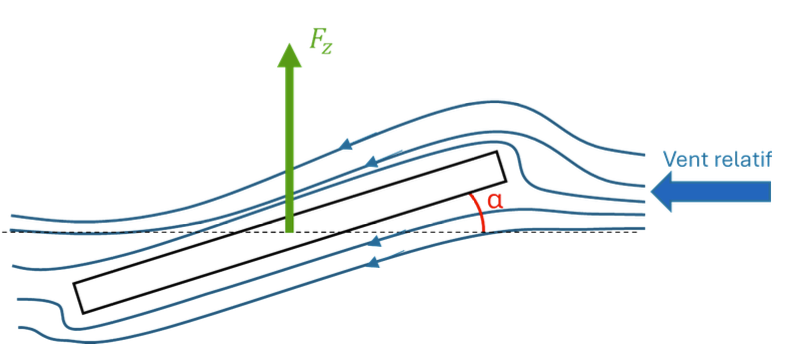
- Une pale est un parallélépipède rectangle de longueur \(R_p\), de largeur \(l_p\) et d'épaisseur négligeable. Elle est inclinée d'un angle \(\alpha\) par rapport à l'horizontale. La figure 2 présente un schéma de coupe latérale.
|
Figure 2. Schéma en coupe d'une pale d'hélicoptère |
2.2 Choix des valeurs des paramètres
Nous prenons les valeurs suivantes pour la modélisation de l'air :
- Constante des gaz parfait : \(R\) = 8,314 J.mol-1.K-1
- Masse molaire de l'air : \(M_{air}\) = 29 g.mol-1
- Masse volumique de l'air au niveau de la mer : \(\rho_0\) = 1,3 kg.m-3
- Température au niveau de la mer : \(T_{0}\) = 300 K
- Température au niveau du sommet de l'Everest : \(T_{Everest}\) = 250 K
- Altitude de l'Everest : \(H_{Everest}\) = 8 km
- Célérité du son dans l'air ambiant : \(c_{son}\) = 340 m.s-1
Pour la modélisation des pales de l'hélicoptère, nous choisissons les données correspondant au modèle H145 d'Airbus.
- Longueur des pales : \(R_{p}\) = 5 m
- Largeur des pales : \(l_{p}\) = 0,2 m
- Nombre de pales : \(N_p\) = 4
- Inclinaison des pales : \(\alpha\) = 20°
- Vitesse de rotation : \(U = \omega R_p = \frac{2}{3} c_{son}\)
- Coefficient de portance : \(C_{z}\)(20°C) = 1,6
- Masse de l'hélicoptère : \(M\) = 3.103 kg
2.3 Modélisation des pales et force de portance
On considère les pales comme décrites par des parallélépidèdes rectangles, qui sont en rotation à une vitesse angulaire \(\omega\). Cela crée un vent relatif (de vitesse \(U\)) dans le référentiel des pales, et donc une force de portance, dans un régime à haut nombre de Reynolds.
On rappelle que le nombre de Reynolds est défini comme le rapport entre les forces d'inertie et les forces visqueuses. Ici, on a :
$$ R_e = \frac{U l_p \rho_{air}}{\eta_{air}} $$
On trouve un ordre de grandeur de \(R_e \approx\) 106.
La force de portance est dans un permier temps calculée sur une seule pale. Elle évolue de manière quadratique avec la vitesse. La vitesse n'étant pas constante sur toute la longueur de la pale (en effet, proche du rotor elle est beaucoup plus faible que de la vitesse d'un point en bout de pale), on calcule alors une vitesse moyenne sur la longueur de la pale.
Pour un élément infinitésimal de surface \(dS = ldr\), à une altitude \(z\) donnée, on a : :
$$ dF(z) = \frac{1}{2} \rho(z) \omega^2 r^2 l C_z(\alpha) dr $$
On en déduit, en intégrant pour r allant de 0 à \(Rp\), la norme de la force de portance moyenne qui s’exerce sur une pale pour une altitude \(z\) :
$$ F(z) = \frac{1}{6} \rho(z) \omega^2 R_p^3 l_{p} C_z(\alpha) ~~~~~~~~~~\big(Eq1\big)$$
Avec \(\rho (z)\) la masse volumique de l'air qui dépend de l'altitude de l'hélicoptère.
2.4 Hypothèse de l'atmosphère isotherme
On a maintenant besoin de connaître la dépendance de la masse volumique de l'air en fonction de l'altitude \(\rho (z)\) pour évaluer l'altitude à laquelle la force de portance ne compense plus le poids l'hélicoptère.
La relation fondamentale de la statique des fluides s'écrit :
$$ \frac{dP(z)}{dz} = - \rho(z) ~ g ~~~~~~~~~~\big(Eq2\big)$$
Nous considérons que l'atmosphère est isotherme à la température \(T_0\) et supposons que l'air est un gaz parfait. La relation des gaz parfaits pour un volume \(V\) donne :
$$ P(z) V = n(z) R T_0 $$
soit
$$ P(z) = \frac{R T_0}{M_{air}} \rho(z) $$
En dérivant selon \(z\) et en utilisant (Eq2), on obtient :
$$ - \rho(z) g = \frac{R T_0}{M_{air}} \frac{d\rho(z)}{dz} $$
En posant \(H = \frac{R T_0 }{M_{air} g} \) on obtient :
$$ \frac{d\rho(z)}{dz} + \frac{1}{H} \rho(z) = 0 $$
On en déduit finalement :
$$ \rho(z) = \rho_0 \exp{ \left( \frac{-z}{H} \right)} $$
où \(\rho_0\) correspond à la masse volumique de l'air au niveau de la mer.
2.5 Altitude maximale
En utilisant (Eq1) et en appliquant le principe fondamental de la dynamique à l'hélicoptère à l'équilibre (pour \(z_c\)), on a la force de portance qui égale le poids de l'hélicoptère :
$$ F(z_c) = M g $$
Soit :
$$ \frac{n_{pales}}{6} \rho_0 \exp{ \left( \frac{-z_c}{H} \right)} \omega^2 R_p^3 l_p C_z (\alpha) = M g $$
Ce qui donne l'altitude critique \(z_c\) :
$$ z_c = H \ln \Biggl( \frac{n_{pales}\rho_0 \big(\frac{2}{3} c_{son}\big)^2 R_p^3 l_p C_z (\alpha)}{6 M g} \Biggl) $$
À l'aide des valeurs numériques données plus haut, on trouve : \(z_c \approx\) 7 073 m
3. Discussion des résultats
Tout d'abord, notons que l'on trouve un résultat du même ordre de grandeur que ce qui est observé en réalité. En effet, de tels hélicoptères sont capables de monter jusqu'à 6 000 m d'altitude d'après leurs constructeurs. Cependant, quelques remarques sont à faire :
- La formule trouvée pour \(z_c\) induit une forte dépendance par rapport aux paramètres choisis, et une légère variation de la vitesse des pales ou de \(C_z\) par exemple, amène à une différence notable pour la valeur de \(z_c\), qui parfois s'éloigne fortement de la réalité, bien que l'ordre de grandeur de quelques kilomètres soit toujours respecté.
- L'hypothèse de l'atmosphère isotherme est réaliste. La température en haut de l'Everest est plus faible d'environ 50 K par rapport à celle au niveau de la mer, ce qui ne change pas significativement le résultat.
- On a considéré le coefficient de portance \(C_z\) comme uniquement dépendant de \(\alpha\), et comme seul paramètre influencé par \(\alpha\). Ce choix est à discuter puisque \(C_z\) est un paramètre central dans la dynamique de l'air sur les pales.
- La géométrie des pales a été fortement simplifiée pour limiter la complexité des calculs. En réalité, le profil des pales est plus hélicoïdal, d'épaisseur et de surface d'attaque variables.
- Enfin, l'air qui arrive sur une pale a été perturbé par la pale précédente, et n'est donc pas au repos à l'infini. Le nombre de pales n'a donc pas que pour effet d'augmenter la portance mais influe sur la recirculation de l'air également. Il n'est donc, a priori, pas possible de simplement augmenter le nombre de pales pour monter plus haut.
Pour citer cet article :
Quelle est la hauteur maximale à laquelle un hélicoptère de secourisme peut voler?, Romain Bothéreau, Sidoine Terme, Martin Trebosc, septembre 2025. CultureSciences Physique - ISSN 2554-876X, https://culturesciencesphysique.ens-lyon.fr/ressource/helicoptere.xml