Activer le mode zen
Ressource au format PDF
Classification
Simulations du phénomène de diffraction
14/12/2020
Résumé
Cet article propose des simulations, animations et illustrations sur le phénomène de diffraction. Il est inspiré de la vidéo de la Physique animée « La diffraction ».
Table des matières
1. Introduction
Les premiers textes que l'on retrouve sur la diffraction sont ceux du Père Francesco Grimaldi (1618 – 1663) [1] qui s’intéresse en premier de manière détaillée au phénomène de diffraction dès 1650. Mais ses écrits ne seront connus que plus tard, cités par Honoré Fabri ou encore Isaac Newton. Plus d'un siècle plus tard, en 1818, Augustin Fresnel (1788 - 1827), propose une interprétation simple du phénomène, permettant de comprendre les figures de diffraction observées à grande distance des obstacles. Il s'appuie notamment sur la théorie ondulatoire de la lumière proposée par Christian Huygens (1629 – 1695) publiée en 1690. Depuis l’avènement de la théorie de l’électromagnétisme de Maxwell (1831 - 1879), la diffraction apparaît comme une conséquence directe des équations de Maxwell.
 Source : Wikimedia. |
On peut observer le phénomène de diffraction lorsqu’une onde, qu’elle soit électromagnétique ou mécanique, rencontre un obstacle qui masque une partie du front d’onde.
La diffraction est perceptible dès que les dimensions caractéristiques de l'obstacle ne sont pas grandes vis–à-vis de la longueur d’onde.
Nous proposons, ici, des simulations et animations pour mettre en évidence ce phénomène.
2. Propagation d'une onde - Principe de Christian Huygens
Christian Huygens émit l’hypothèse de la nature ondulatoire de la lumière. Sa modélisation de la propagation de la lumière est la suivante : chaque point d’une surface d’onde peut être considéré comme une source secondaire, et la surface d’onde à un instant postérieur est l’enveloppe des surfaces d’onde provenant de cette infinité de sources secondaires, figure 2.
Source - © 2020 CultureSciences Physique |
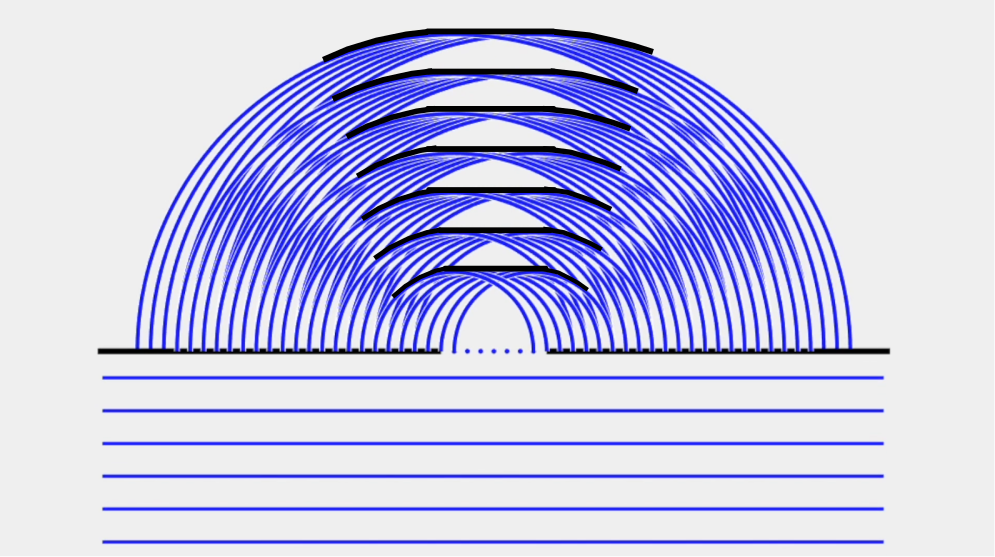
Nous allons maintenant nous intéresser à la propagation d'une onde dans l'espace. En se basant sur le principe d'Huygens, il faudrait une infinité de sources secondaires pour représenter une onde plane.
Sur la figure 3, nous n'avons représenté seulement qu'une vingtaine de sources ponctuelles, l'onde ne rencontre pas d'obstacle. Le front d'onde résultant est surligné en noir, à droite, figure 4.
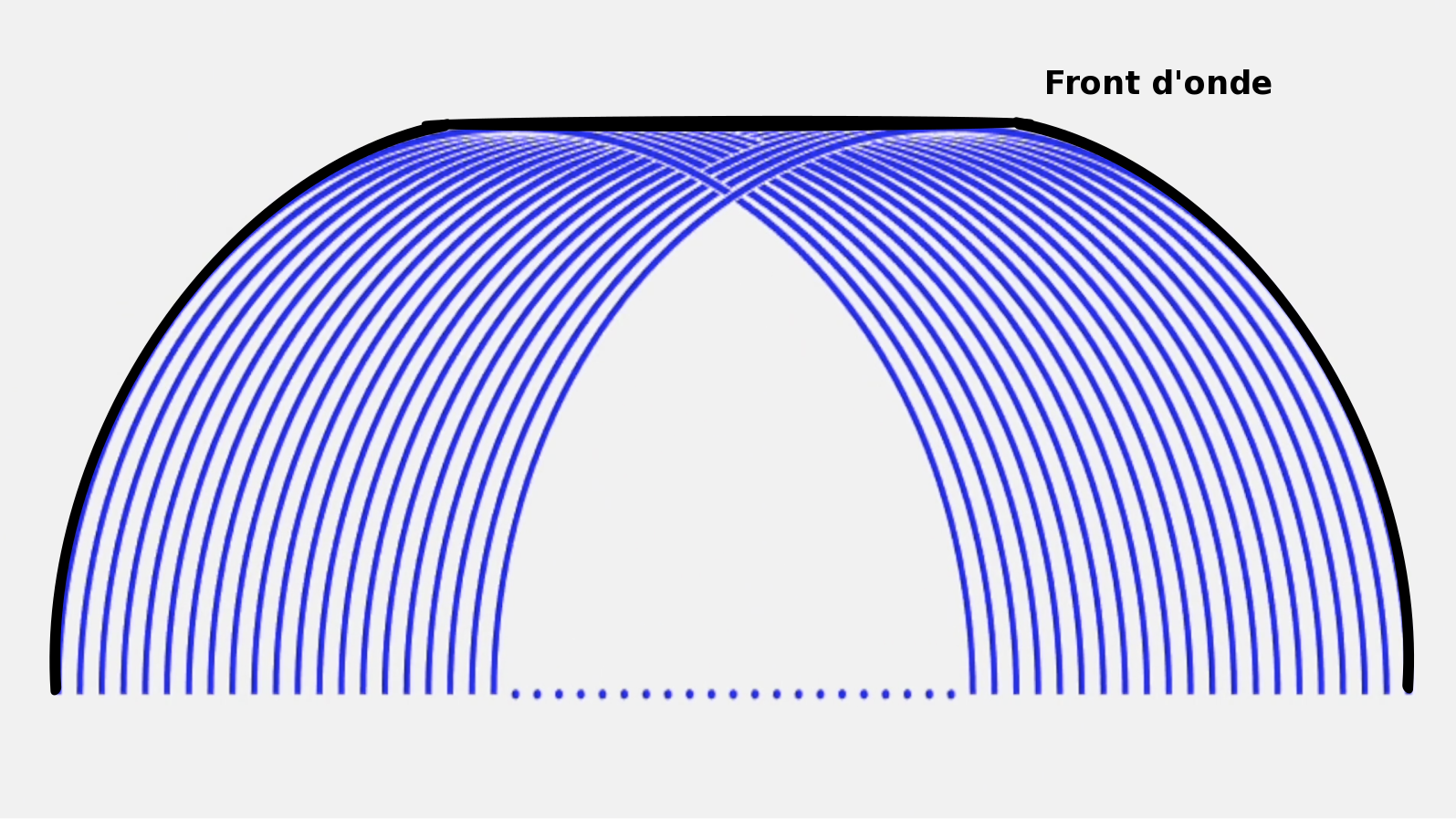 . |
3. Diffraction d'une onde par une fente
Maintenant, que va-t-il se passer en présence d'un obstacle comme une fente ?
On peut ainsi comprendre qualitativement le phénomène de diffraction : quand l'onde plane arrive sur une ouverture de largeur d, une partie des sources secondaires est supprimée.
Si la taille de l’ouverture est grande devant la longueur d’onde, l’onde plane est finalement peu perturbée devant l'ouverture, figures 5 et 6.
Source - © 2020 CultureSciences Physique |
Par contre, si la largeur de l'ouverture se rapproche de la longueur d’onde, seules quelques sources secondaires passent et l’onde résultante sera essentiellement sphérique en aval de l’ouverture, figure 7.
Source - © 2020 CultureSciences Physique |
4. Diffraction d'une onde par un obstacle plan
De la même manière, une partie des sources secondaires sera arrêtée au contact d’une paroi, conduisant ainsi à la propagation d’ondes sphériques générées au contact de celle-ci, figure 8.
Source - © 2020 CultureSciences Physique |
5. Répartition de l'intensité
Jusqu'à présent nous ne nous sommes intéressés qu'au front d'onde. La diffraction modifie aussi la répartition de l'énergie de l'onde résultante. C’est Augustin Fresnel qui en donna l’explication : toutes les sources secondaires qui se retrouvent en aval de l’ouverture ou de la paroi vont interférer entre elles et conduirent, ainsi, à des zones de forte lumière ou, au contraire, à des zones d’obscurité. Le phénomène de diffraction apparaît alors comme un phénomène d’interférences multiples entre ces sources secondaires.
En guise d'illustration, la figure 9 montre l'intensité codée en fausses couleurs de l'onde résultante de deux sources secondaires côte-à-côte. Sur le front d'onde, on trouve des zones avec peu d'énergie et des zones beaucoup plus contrastées. La figure 10 permet de mieux reprérer les minima et maxima, à l'aide d'une visualisation en 3 dimensions.
Simulation réalisée en modifiant le code initial de Praveen Ranganath (2020). 2D Interfering waves, MATLAB Central File Exchange. |
6. Résultats expérimentaux
On retrouve ces résultats dans les expériences classiques utilisant la cuve à onde. En modifiant la disposition des obstacles, on retrouve les différentes formes d'onde en fonction de la largeur de l'ouverture par rapport à la longueur d'onde, figure 11.
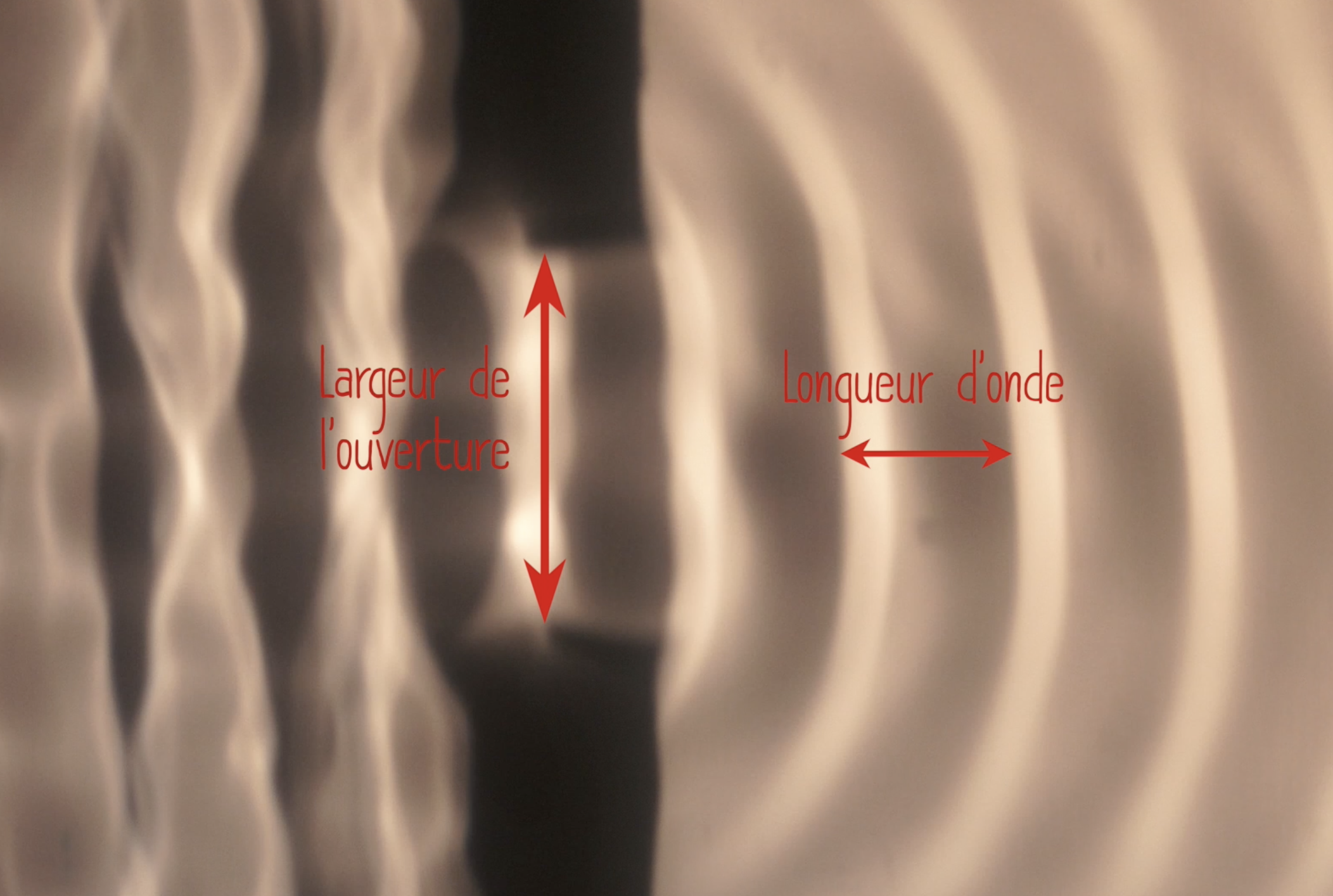 Figure 11. Longueur d'onde et largeur de l'ouverture |
Figure 12, lorsque l’ouverture est grande devant la longueur d'onde, on retrouve une propagation d’onde quasi-plane simplement limitée par la largeur de l’ouverture. L’intensité de l’onde est maximale en face de l’ouverture et diminue lorqu’on s’en écarte.
Figure 13, lorsque l'ouverture est petite devant la longueur d'onde, la forme de l'onde résultante est très modifiée. Au passage de l’obstacle l’onde n’est plus plane mais devient circulaire.
La longueur d’onde n’est pas affectée par le passage de l’obstacle.
Il est difficile de bien percevoir le contraste donc la répartition de l'énergie des ondes sur les photos précédentes. Remplaçons la fente par un obstacle, figure 14. L’onde vient intercepter les deux bords, c’est comme si l’on avait créé deux ouvertures. On remarque que les ondes se propagent derrière l’obstacle.
Maintenant il est plus facile d'observer, derrière l'obstacle, des zones claires et sombres, correspondant aux extrema d'amplitude des ondes et des zones peu contrastées, mettant en évidence des interférences entres les ondes donnant des résultantes nulles, c’est à dire sans modification de la hauteur d’eau localement dans le temps.
De la même manière, en optique, lorsqu'on place un obstacle, ici un fil, sur le faisceau lumineux d'un laser, on retrouve la répartition d'intensité lumineuse dans les taches de diffraction, figures 15 et 16.
 Figure 15. Fil placé devant un faisceau lumineux |
7. La diffraction dans la nature
Les manifestations du phénomène de diffraction se retrouvent de manière courante dans notre quotidien. Par exemple, lorsque nous observons la modification de la forme des vagues ici sur une côte à Chypre, figure 17. La photo permet de visualiser de manière spectaculaire la transformation de la forme d’onde des vagues avant et après le passage des brises vagues.
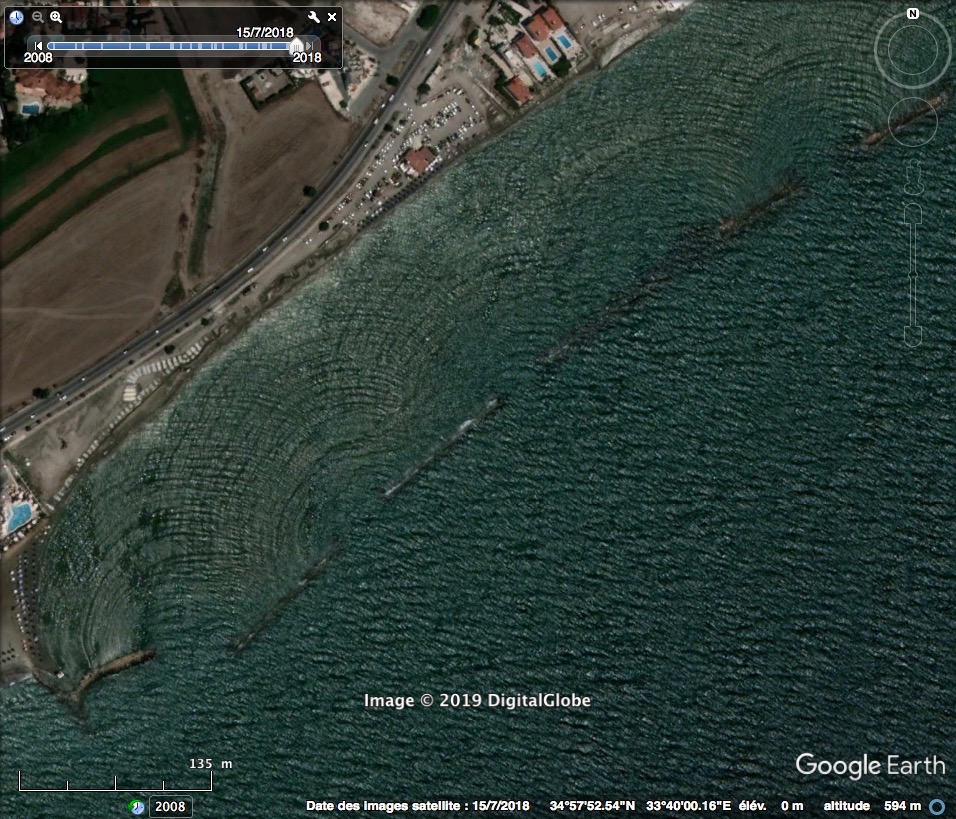 Source : Google Earth. Figure 17. Chypre, 34°57'52.44"N |
La photographie, figure 18, a été prise sur la côte sud-africaine. Cette fois, deux jetées viennent au devant de la mer. On voit clairement les vagues s’enrouler autour de la plus longue jetée pour finalement laisser un port où règne un calme plat. C’est comme si le bout de la jetée se comportait comme une source ponctuelle.
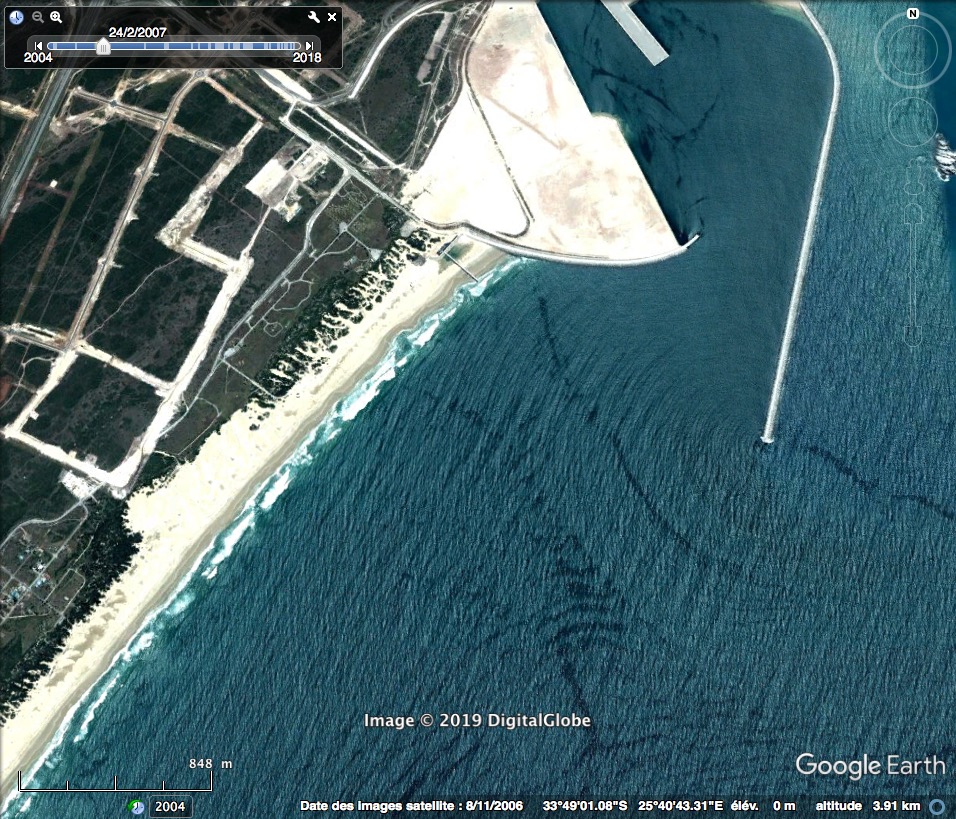 Source : Google Earth. Figure 18. Afrique du Sud, 33°49'01.88"S |
La photographie, figure 19, a aussi été prise sur la côte sud-africaine. Cette fois, une seule jetée referme le port. Les vagues s’enroulent autour d'elle, les ondes sont visibles à l'intérieur du port comme on l'a vu dans la simulation plus haut, lorsque l'obstacle était une paroi.
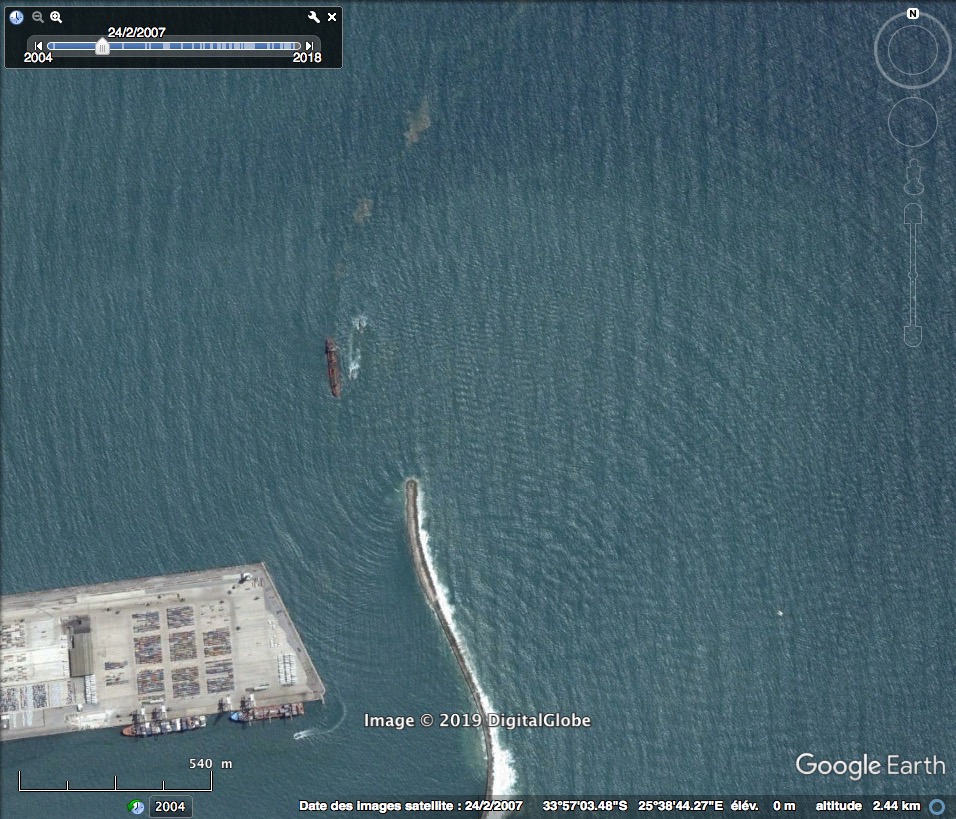 Source : Google Earth. Figure 19. Afrique du Sud, 33°57'03.48"S |
Visionner la vidéo de la physique animée sur « La diffraction ».
Pour citer cet article :
Simulations du phénomène de diffraction, Chareyron, Granier, Taberlet, décembre 2020. CultureSciences Physique - ISSN 2554-876X, https://culturesciencesphysique.ens-lyon.fr/ressource/simu-diffraction.xml