Étude énergétique du saut à la perche

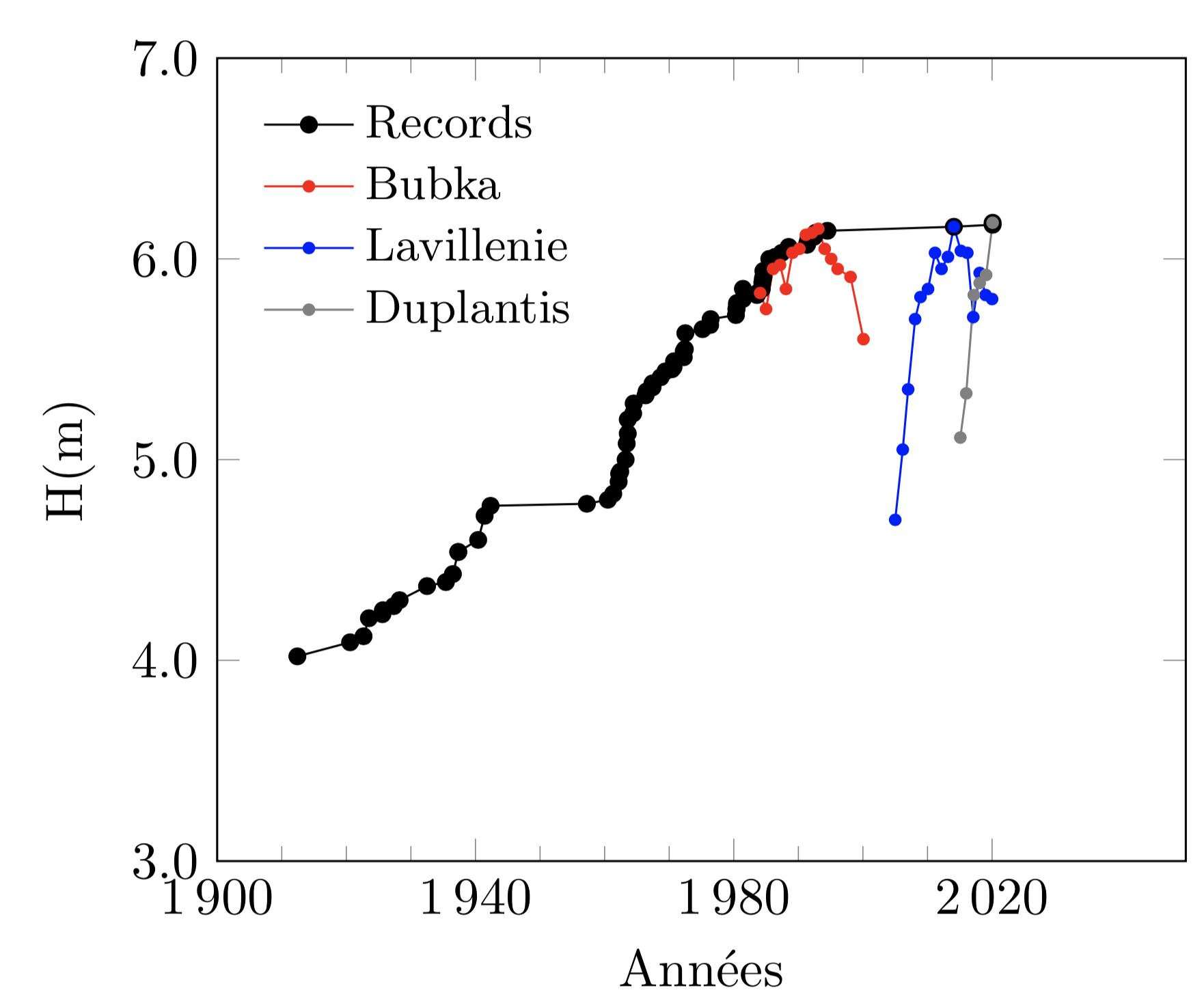
Le saut à la perche a pris ses racines dans la Grèce Antique où des perches rigides en bois étaient utilisées afin de franchir des ruisseaux ou des haies de faibles hauteurs. Sport rendu Olympique en 1896 par Pierre de Coubertin, les hauteurs franchies n’ont depuis cessé d’augmenter grâce aux évolutions du matériel et des techniques de saut, passant ainsi de 3,30 m à 6,18 m en un peu plus de 100 ans (record détenu par le suédois Armand Duplantis [ref1] depuis 2020, figure 1).

Pourtant, à y regarder de plus près, seuls vingt-six athlètes ont franchi la barre mythique des 6 m en 37 ans et uniquement trois ont passé les 6,10 m. En outre, un titre mondial ou olympique se gagne le plus souvent en sautant une barre inférieure à 6 m. Que justifie un tel écart de performances ? Nous avons cherché des éléments de réponse à cette question en travaillant sur les échanges énergétiques pendant la phase de vol.

Figure 1.  Evolution des records du monde du saut à la perche et des meilleures performances annuelles des 3 meilleurs performeurs masculins

Un concours de saut à la perche, consiste à franchir la barre la plus haute possible avec pour seul outil une perche pouvant être de longueur, de diamètre et de constitution variable (en pratique les perches utilisées par les hommes de haut niveau mesurent entre 4,90 m et 5,30 m, ont une masse d’environ 2 kg et un diamètre de typiquement 30 mm). Au-delà de « l’effet tunnel »^[1] lié à la déformation du corps du sauteur [ref2] l’énergie potentielle du centre de masse de l’athlète est un bon indicateur de la performance d’un saut. D’un point de vue énergétique, l’athlète se doit d’accumuler le plus d’énergie cinétique puis potentielle possible afin d’amener son centre de masse le plus haut possible. Mais pourquoi donc utiliser une perche ?

Prenons comme exemple un athlète de 80 kg ayant un centre de masse initialement situé à 1 m du sol. Afin d’atteindre la hauteur légendaire des 6 m, il doit accumuler une énergie potentielle \( E_p = m g \Delta z \) = 4 000 J, où \( \Delta z\) = 5 m est le gain de hauteur du centre de masse. Pour ce faire, il essaye simplement dans un premier temps de sauter à pieds joints.

Le temps caractéristique dont il dispose pour accumuler cette énergie est de l’ordre 0,3 s (temps entre la position basse en squat et le décollage des pieds). Afin d’atteindre l’objectif fixé, il est donc censé produire une puissance moyenne de 13,3 kW, tandis que les puissances maximales que sont capables de générer les plus grands sportifs ne dépassent pas les 1,8 kW (soit un gain en hauteur de \( \Delta z = \frac{0,3 \times 1800}{80 \times 10 }\approx\) 70 cm cm). Cette première tentative se solde donc par un échec.

Cet athlète aux jambes robustes se rend très vite compte que le moyen le plus efficace d’accumuler une telle quantité d’énergie n’est ni plus ni moins qu’une bonne course d’élan, permettant d’augmenter son capital énergétique quadratiquement avec sa vitesse : \( E_c = \frac{1}{2} mv^2\).

Afin d’obtenir les 4 000 J évoqués plus haut, il doit ainsi atteindre la vitesse moyenne de 10 m/s (36 km/h), valeur élevée mais néanmoins atteignable par notre athlète de haut niveau aux capacités exceptionnelles (le « Tsar » Serguei Bubka [ref3] (1,83 m pour 80 kg) avait une vitesse de course d'élan, perche en main mesurée à 10,02 m/s).

A priori, en supposant une conservation énergétique totale, courir deux fois plus vite permettrait de sauter quatre fois plus haut. Cependant, alors que notre athlète « file comme le vent » et atteint la vitesse adéquate à la réussite de son saut, un nouveau problème se pose à lui : comment transférer efficacement son impulsion horizontale en impulsion verticale ?

En témoigne le record de saut en hauteur (2,45 m établi par le cubain Javier Sotomayor en 1993 [ref4]), une simple impulsion verticale en fin de prise d’élan ne permet qu’une conversion énergétique à rendement faible (inférieure à 30%). Après avoir augmenté le temps d’accumulation de son capital énergétique grâce à la course d’élan, il doit désormais augmenter le temps de conversion énergétique afin de mieux conserver l'énergie accumulée.

C’est à ce moment que notre athlète décide d’employer une perche de saut en matériau composite capable de stocker de l’énergie en se déformant puis de la restituer en revenant à son état initial, et ce avec très peu de pertes. L’athlète stocke ainsi temporairement dans sa perche une partie de l’énergie mécanique accumulée durant la prise d’élan, puis tâche de faire en sorte que cette dernière lui restitue cette énergie en le renvoyant le plus verticalement possible. Le temps de flexion/dépliement d’une perche lors d’un saut est de l’ordre de 1 s, tandis que le temps caractéristique d’une impulsion est de 0,1 s. Notre athlète a donc multiplié par 10 le temps de conversion énergétique. Mais qu’en est-il du rendement ?

Ici nous faisons l’hypothèse que tout est dans le temps du transfert. Une autre hypothèse possible consiste à raisonner sur les variations d’impulsion par unité de temps c’est à dire sur les forces :

Afin de quantifier ce rendement, nous avons cherché à accéder aux énergies de l’athlète et de sa perche au cours du saut. Il nous fallait pour cela obtenir la cinématique du saut tout en restant le moins intrusif possible pour l’athlète.

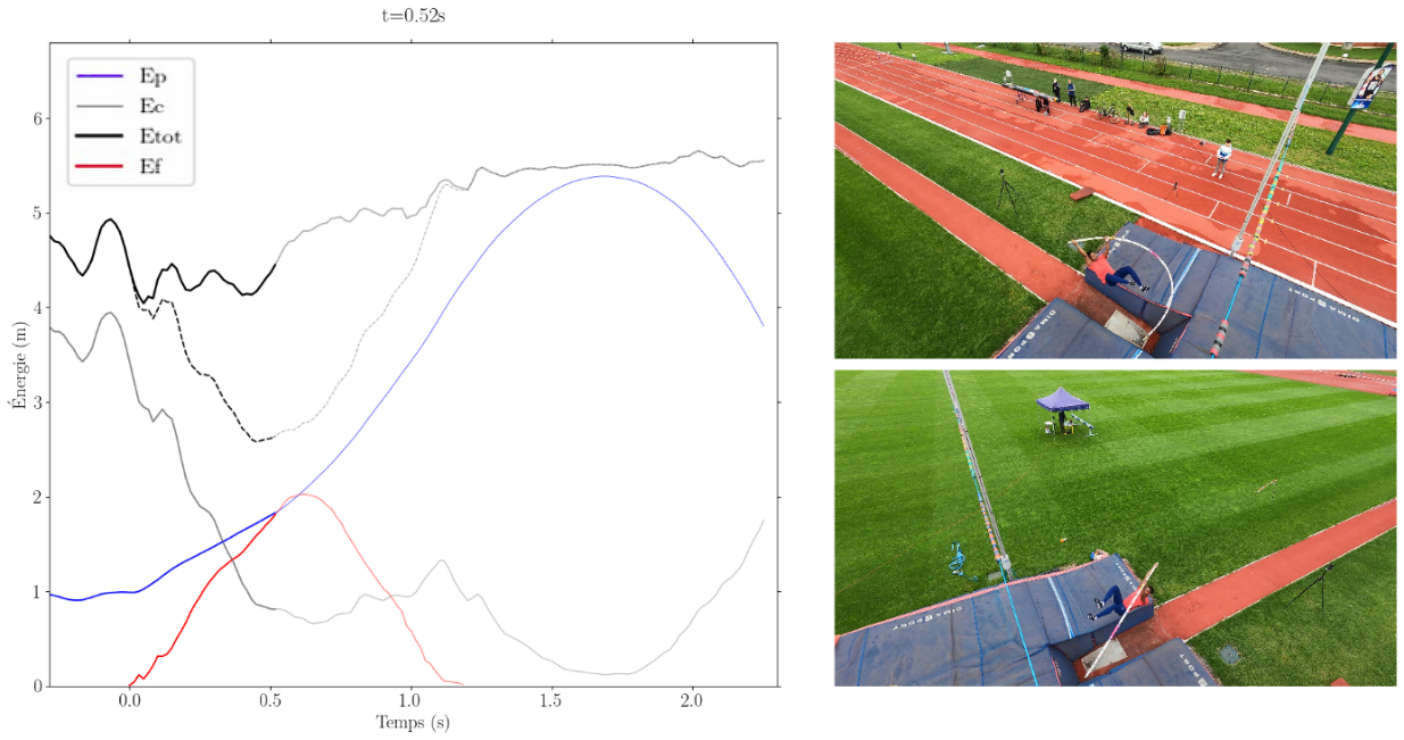
Nous avons donc mis en place une méthode de reconstruction tridimensionnelle consistant à trianguler la scène à l’aide de deux caméras fixées au sommet des poteaux du butoir, figure 2.

Figure 2.  Vue des caméras

Figure 3.  Scène d'un saut reconstruite en 3D

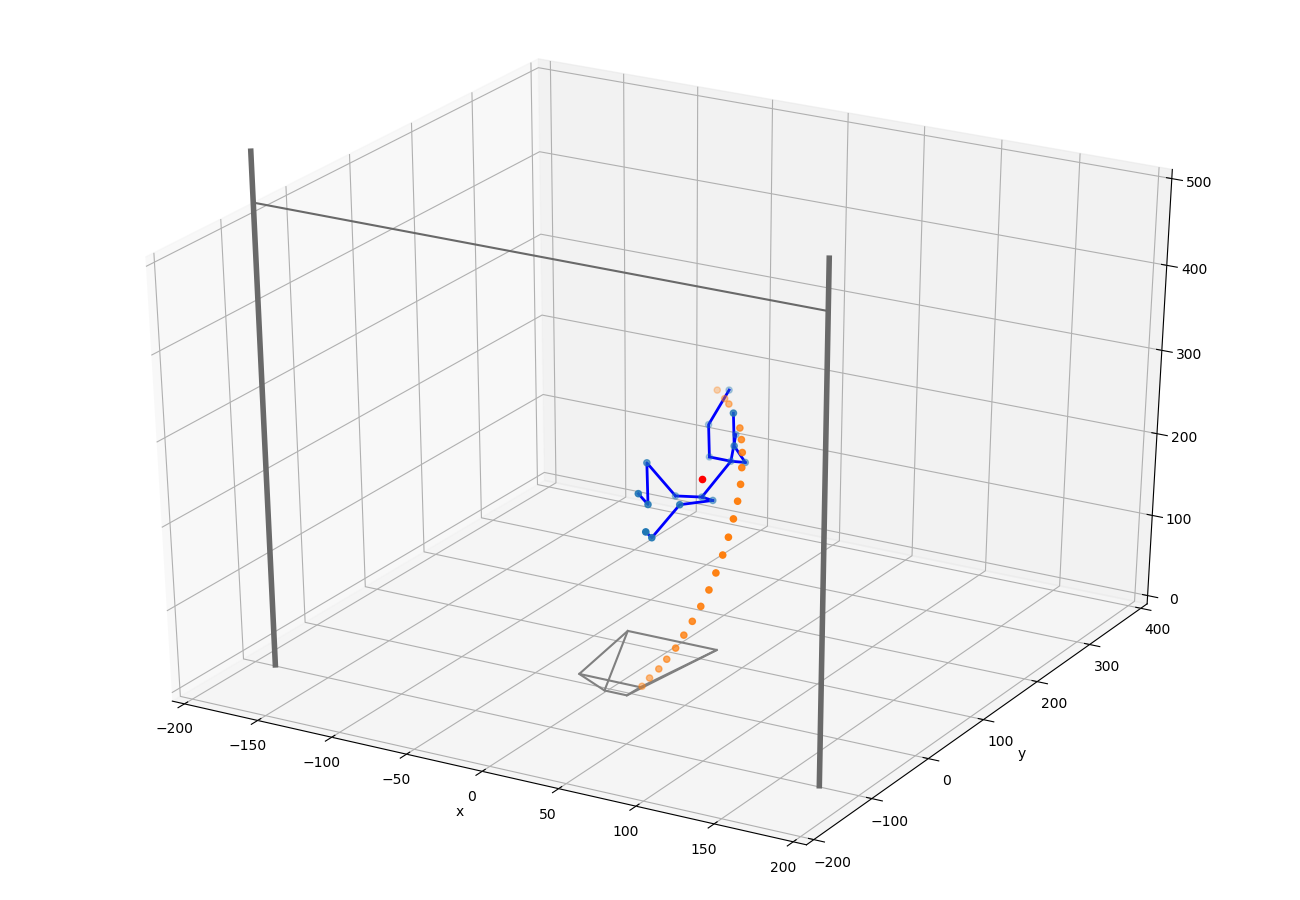
Le centre de masse de l’athlète est repéré grâce aux tables de pondérations de DeLeva [ref5] ce qui permet de réduire l’analyse du corps humain en l’étude de segments rigides (les bras, les avant-bras, le tronc, etc) dont la masse et le centre de gravité sont tabulés. Ces segments sont repérés dans les images par leurs extrémités (les coudes, les mains, les épaules, etc). La connaissance de la position de ces segments dans l’espace 3D réel et donc de la position de leur centre de masse permet de remonter à la position du point rouge visible figure 3 correspondant au centre de masse global de l’athlète.

Figure 4.  Rubans adhésifs repérés par les deux caméras

La cinématique de la perche est quant à elle repérée par des repères disposés au préalable sur tout son long (figure 4). C’est au total une vingtaine de points (en orange sur la figure 3) qui permettent, après une régression polynomiale dans l’espace réel, de capturer la déformation de la perche.

Les enregistrements ont été réalisés sur le perchiste Alioune Sène (25 ans) qui porte son record personnel à 5,74 m depuis février 2022 [ref6].

Sur la figure 5, nous pouvons retrouver le mouvement du perchiste du perchiste Alioune Sène, à l'aide de la modélisation du corps humain en segments rigides, pour un saut réalisé à 5,40 m.

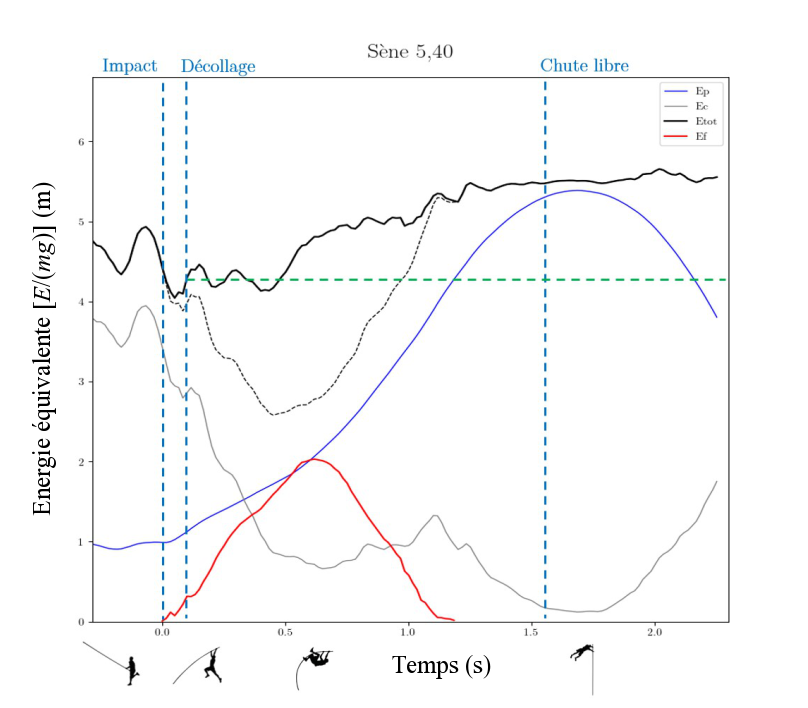
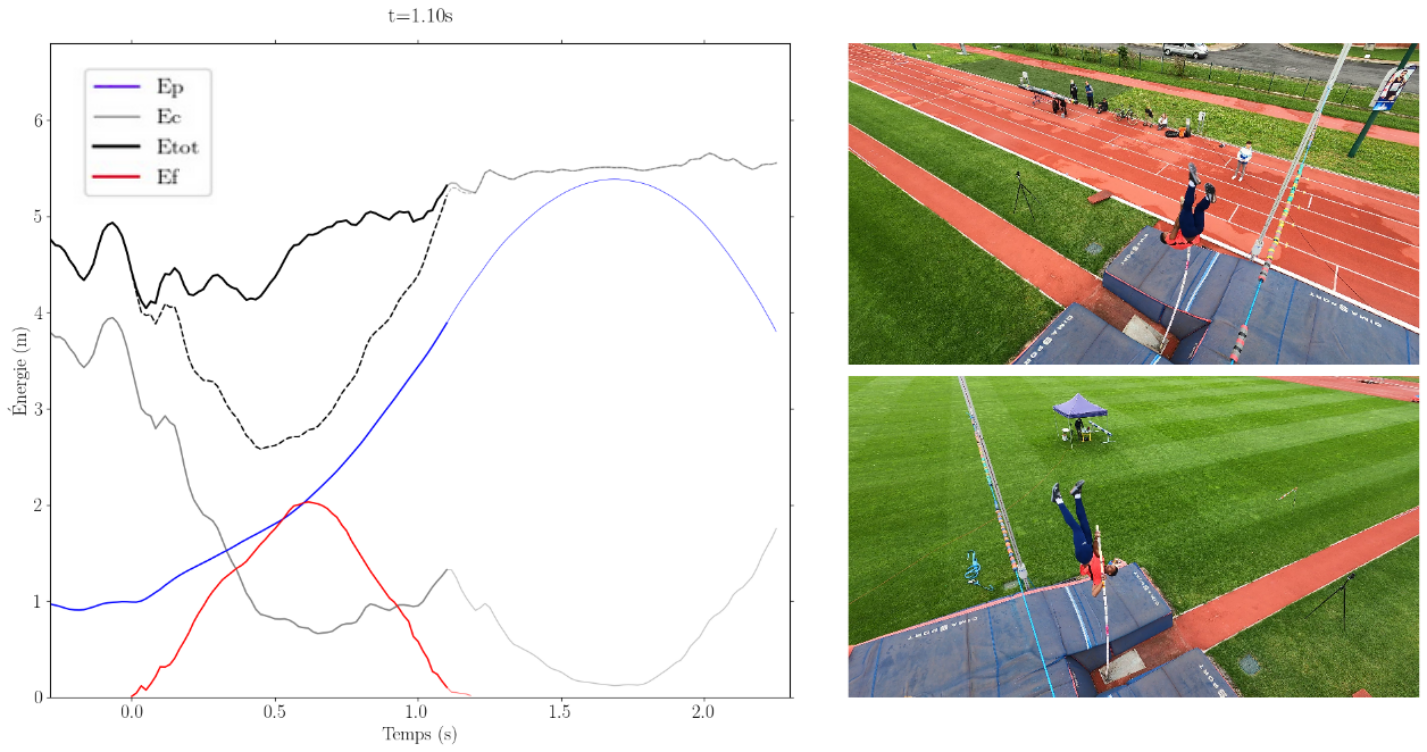
Nous proposons maintenant de décomposer le mouvement et de représenter les différentes énergies en jeu (potentielle, cinétique, de flexion et totale) au cours du temps, figure 7.

Figure 7.  Évolution des différentes énergies lors d'un saut en fonction du temps L'énergie potentielle est représentée en bleu, l'énergie cinétique en gris, l'énergie de flexion de la perche en rouge et l'énergie totale en noir. En pointillés est représentée l'énergie mécanique du perchiste (énergie potentielle + énergie cinétique).

Prenons comme système d’étude le perchiste et sa perche. Comme évoqué précédemment, ce système est composé de deux corps qui échangent de l’énergie durant le saut. Faisons dans un premier temps l’hypothèse que le corps humain est rigide et inactif durant la phase de vol, et appliquons un bilan énergétique à notre système :

$$ \Delta E_{tot} = \Delta(E_c + E_p +E_f) = - W_{pertes} $$

Avec \( W_{pertes} > 0 \)

\( E_c \) est l'énergie cinétique de l'athlète (en gris), \( E_p \) est l'énergie potentielle de l'athlète (en bleu), \( E_c \) est l'énergie de flexion de la perche (en rouge, figure 6).

Le terme de perte énergétique est principalement lié au choc de la perche dans la butée qui donne naissance à des ondes se propageant au sein du matériau, ainsi qu’à de l’absorption musculaire.

D’après cette relation, l’énergie totale ne pourrait que diminuer après le décollage, ce qui est contraire à la croissance de la courbe noire observée en figure 7. En effet, le sauteur est encore capable d’accroître son capital énergétique durant la phase de vol en travaillant sur ses bras, ses abdos, etc.

Considérons donc l’athlète comme un corps actif capable d’injecter de l’énergie durant la phase aérienne. (Au passage, on note que l'énergie cinétique de la course est aussi injectée par l'athlète, mais ici nous noterons les contributions uniquement aériennes de l'athlète dans le terme \( W_{athlète} \)). Le bilan énergétique total du système {perchiste actif + perche} est donné par la relation :

$$ \Delta E_{totale} = \Delta(E_c + E_p +E_f) = W_{athlète} - W_{pertes} $$

Prenons néanmoins garde au signe de \( W_{athlète} \) qui peut être positif ou négatif. Pour s’en convaincre, imaginons un sauteur sur un trampoline. S’il est rigide, inactif et que l’on néglige les pertes, l’énergie totale du système {sauteur + perche} se conserve et le sauteur remontera toujours à la même altitude. Si en revanche il décide de redonner une impulsion avec ses jambes en phase avec la remontée du trampoline, \( W_{athlète} \) est alors positif puisque l’énergie dépensée permet d’augmenter l’énergie totale du système. Cependant, s’il décide de replier ses jambes lors de la phase de remontée du trampoline, l’énergie dépensée ira à l’encontre de la restitution énergétique du trampoline vers l’athlète, impliquant ainsi une baisse de l’énergie totale, \( W_{athlète} \) est donc négatif. Faire preuve de non-rigidité peut donc être un avantage tout comme un inconvénient du point de vue de la conservation globale. Dans le cas du saut à la perche, si l’athlète laisse filer sa perche lors de la phase de restitution sans être totalement gainé, il perdra l’énergie emmagasinée jusqu’alors.

On semble par ailleurs systématiquement observer sur la courbe de l’énergie totale la présence de plateaux à des temps très similaires. Il existe donc deux phases principales d’injection d’énergie durant la phase aérienne : le retournement au cours duquel l’athlète force sur ses abdos (figure 8), puis le redressement lorsqu’il s’étend verticalement (figure 9).

Figure 8.  Phase de retournement - Alioune Scène, saut à 5,40 m

Figure 9.  Phase de redressement - Alioune Scène, saut à 5,40 m

Réjouissons-nous car le saut à la perche n’a pas fini de nous étonner. Bien que l’humain soit limité en vitesse lors de la course d’élan, d’autant plus lorsqu’il tient une perche à bout de bras, il peut encore accumuler de l’énergie après le décollage afin d’atteindre des altitudes toujours plus élevées. Cette étude a mis en évidence l’importance de deux phases négligées en introduction qui sont les pertes à l’impact que l’on veut minimiser et l’activité aérienne du perchiste que l’on veut maximiser. Outre un sprint rondement mené, l’athlète se doit d’optimiser ces deux aspects afin de tutoyer les sommets. Autrement dit, il faut à la fois courir vite et savoir injecter de l’énergie à point !

Les données récoltées pour cette étude sont gracieusement mises à disposition. Il est ainsi possible de travailler sur des données réelles en classe.

Télécharger le fichier comprenant les données énergétiques en fonction du temps :