Energie et référentiels

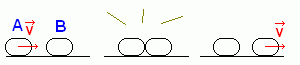
On a considéré deux palets A et B identiques de masse m, B étant immobile, et A glissant sans frottement vers lui à la vitesse v. Les deux palets entrent en collision via un choc élastique. On sait que, dans ce cas-là, après le choc, la vitesse de A va être nulle : il l'aura communiquée entièrement à B qui se déplacera désormais à la vitesse v.

Gabrielle Bonnet

A gauche, les deux palets avant le choc, au milieu, pendant le choc et à droite, après.

Figure 1. Variations d'énergie cinétique de deux palets A et B de masses identiques

Les variations d'énergie cinétique de A et de B sont faciles à calculer : l'énergie cinétique de A vaut E = 1/2 m v² avant le choc, et elle est nulle après le choc, d'où une variation d'énergie cinétique égale à - E. Celle de B vaut 0 avant le choc et E après, d'où une variation d'énergie cinétique qui vaut + E.

Si l'on se place à présent dans le référentiel dans lequel A est immobile avant le choc, tandis que B va à la vitesse - v, après le choc, A ira à la vitesse - v et B sera immobile. Dans ce cas, l'énergie cinétique de A est zéro avant le choc, E après, ce qui fait une variation d'énergie + E, tandis que B passe de E à 0, ce qui fait une variation d'énergie - E.

Le choc, élastique dans un référentiel le reste bien dans le deuxième (variation totale d'énergie cinétique nulle), mais ni les énergie cinétiques des palets, ni même les variations de ces énergies ne sont identiques.

Ainsi, la conception d'une énergie cinétique, ou même d'une variation d'énergie cinétique "absolue", indépendante du référentiel, ne semble pas avoir de sens.

Considérons un système composé des points matériels M_i, de masse m_i, et de vitesse, dans le référentiel galiléen R, v_i à l'instant t, v'_i à l'instant t'.

Dans un deuxième référentiel galiléen R*, les vitesses des points matériels sont v_i - V à l'instant t, v'_i - V à l'instant t'.

La variation d'énergie cinétique du système, entre les instants t et t', vaut, dans le référentiel R, Δ E = ∑ m_i v'_i² - ∑ m_i v_i²

De même, on calcule la variation d'énergie cinétique dans le référentiel R* et on montre qu'elle vaut :

Δ E* = Δ E + ∑ m_i (v'_i - v_i) . V

soit

Δ E* = Δ E + ΔP . V

ΔP est la variation d'impulsion totale du système, qui est aussi la variation d'impulsion du centre de gravité du système. On trouve donc que, si le système est isolé, l'énergie cinétique du système dépend du référentiel considéré, mais ses variations au cours du temps n'en dépendent pas (variation d'impulsion totale du système nulle), mais, dans le cas général, la variation d'énergie cinétique du système au cours du temps n'est pas la même dans tous les référentiels.

Nous avons l'habitude de considérer l'énergie potentielle avec "précaution" : plus exactement, nous savons que, par exemple, l'énergie potentielle de pesanteur près de la surface du globe est définie "à une constante près", nous savons donc que cette énergie potentielle-là, en soi, est un outil utile, mais que sa valeur n'a pas de "sens absolu" : ce qui a un sens physique, ce sont les variations d'énergie potentielle du système.

D'autre part, lorsque plusieurs objets sont en interaction, nous ne pouvons généralement pas définir l'énergie potentielle "d'un seul d'entre eux", puisqu'il s'agit d'une énergie potentielle d'interaction, associée au système de tous les objets en présence et non à un seul (le cas d'un objet en interaction gravitationnelle avec une planète de masse très grande devant celle de l'objet est cependant un peu particulier puisque, dans ce cas, du point de vue mathématique, on peut tout à fait considérer le système "objet" seul comme le système "objet + planète"...).

Nous avons moins l'habitude cependant de prendre autant de précautions avec l'énergie cinétique... Un simple changement de référentiel, pourtant, fait ressortir le fait que la vitesse, et donc l'énergie cinétique, sont eux aussi relatifs à un choix conventionnel, celui du référentiel dans lequel on se place.

De fait, même les variations d'énergie cinétique d'un système non isolé ne sont pas indépendantes du référentiel considéré... Cela ne pose pas de problème pour utiliser les lois et théorèmes de la mécanique (qui restent valable même lorsqu'on passe d'un référentiel galiléen à un autre), mais jette seulement un éclairage peut-être un peu inhabituel sur la notion d'énergie cinétique.