Quelle surface de toile de parachute faut-il prévoir pour éviter que le sauteur ne se casse la jambe à l'atterrissage ?

On s'intéresse ici à ce que signifie concrètement « se casser la jambe » et comment le traduire d'un point de vue physique. Il s'agit d'estimer une contrainte limite à partir de laquelle l'os se casse. Nous faisons l'hypothèse qu'il y aurait rupture si l'os subit une déformation de sa taille de plus de quelques pourcents lors de la réception. Prenons 1% : \(\mathbf{\varepsilon_{seuil}} \approx \) 0,01.

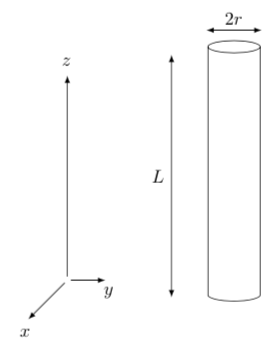
Nous modéliserons le tibia comme un cylindre de longueur \(L\) et de rayon \(r\), figure 2.

Figure 2.  Modélisation du tibia

Il nous faut maintenant déterminer la condition sur la vitesse finale à partir de laquelle la contrainte sur la déformation de l'os est dépassée ou non.

Nous faisons l'hypothèse que la totalité de l'énergie correspondant au choc avec le sol est "absorbée" par le tibia.

On note \(v_f\) la vitesse de la personne à la fin de la chute, son énergie cinétique juste avant le contact avec le sol est donnée par :

$$ \mathcal{E_f} = \frac{1}{2} m v_f^2 $$

L'énergie reçue par l'os à l'impact est donc \(\mathcal{E_f}\), elle correspond au travail de la force \(F\) appliquée sur l'os pour une compression \(\Delta L \).

$$ \mathcal{E_f} = F . \Delta L $$

D'où :

$$ F = \frac{\mathcal{E_f}}{\Delta L} $$

La contrainte appliquée sur l'os s'exprime sous la forme du rapport entre la force appliquée sur l'aire de la section de l'os :

$$ \sigma = \frac{F}{s} = \frac{\mathcal{E_f}}{s \Delta L} = \frac{\mathcal{m v_f^2}}{ 2 s \Delta L} $$

D'après la loi de Hooke, la contrainte \(\sigma\) s'écrit comme le produit du module d'Young, noté \(E\), par la déformation. On a : \(\sigma = E \varepsilon \). Ainsi :

$$ E \varepsilon = \frac{m v_f^2}{2 s \Delta L} $$

Finalement, avec \(\Delta L = \varepsilon L \) :

$$ v_f = \sqrt{\frac{2 s \varepsilon^2 L E}{m}} $$

Si l'on impose comme condition pour ne pas se blesser que la déformation \(\varepsilon \) doit être inférieure à \(\varepsilon_{seuil} \), on obtient la vitesse seuil \(v_{seuil} \) au dessus de laquelle la personne se blesse :

$$ v_f < v_{seuil} = \sqrt{\frac{2 s \varepsilon^2_{seuil} L E}{m}} $$

Pour l'application numérique, nous prendrons : la longueur de l'os \(L\) = 0,5 m, sa section \(s = \pi r^2 \) avec \(r\) = 4 cm, la masse de la personne \(m\) = 80 kg et la déformation seuil \(\varepsilon_{seuil}\) = 0,01. Pour le module d'Young de l'os, nous pouvons raisonnablement prendre une valeur un peu plus élevée que celle correspondant au bois (environ 10 GPa) et largement plus faible que celle correspondant au métal (autour de 150 GPa ). Nous ferons l'application numérique avec \(E\) = 20 GPa.

Le calcul mène alors \(\mathbf{v_{seuil} \approx} \) 11 m.s^-1 donc une vitesse d'impact de l'ordre d'une dizaine de mètre par seconde.

On aurait aussi pu estimer cette vitesse seuil à l'impact en prenant le cas d'une chute libre.

La valeur seuil trouvée précédemment, de l'ordre d'une dizaine de mètres par seconde semble en effet raisonnable ; elle correspond à une chute libre d'une hauteur d'un peu plus de 5 m.

Maintenant que nous avons établi la vitesse limite pour arriver au sol sans se blesser, il faut regarder quelle est la superficie du parachute correspondant à cette vitesse d'impact.

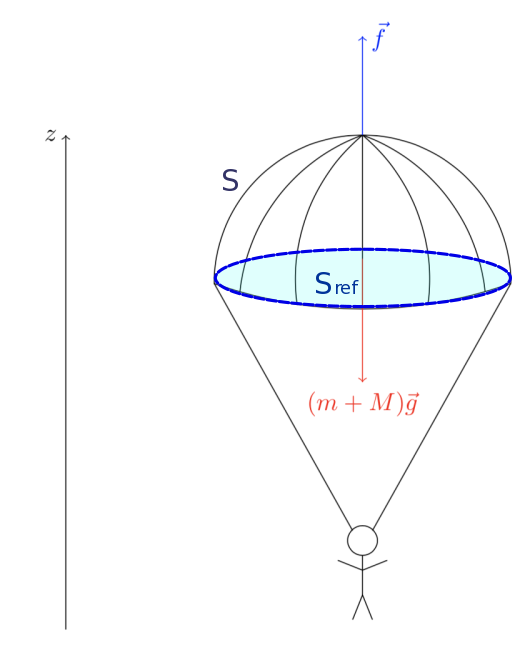
Pour simplifier le modèle, nous allons considérer une toile de parachute demi-sphérique de rayon \( R \).

Figure 3.  Bilan des forces sur le parachute

Dans ce modèle simplifié nous allons considérer les forces suivantes :

Écrivons maintenant le théorème de la résultante dynamique au barycentre de l'ensemble {Personne + Parachute} :

$$ M_T \overrightarrow{a} = \overrightarrow{P} + \overrightarrow{f} $$

On considère le régime stationnaire atteint :

$$ M_T g = \frac{1}{2} \rho S_{ref} C_x v^2 $$

D'où :

$$ S_{ref} = \frac{2 M_T g}{\rho ~C_x ~v^2} $$

La surface réelle du parachute (assimillée à une demi-sphère), est égale à 2 fois la surface de référence, d'où : \(S = 2 S_{ref}\)

Il s'agit maintenant d'obtenir une condition sur la surface du parachute à l'aide de la la vitesse \( v_{seuil} \) précédemment déterminée. On obtient :

$$ S > S_{min} = \frac{4 M_T g}{\rho ~C_x ~v^2_{seuil}} $$

Pour l'application numérique, on prend : \(M_T \approx\) 90 kg, cela représente une personne de 80 kg, et on estime que le poids de la toile, transportée généralement en sac à dos, est d'environ 10 kg. On a : \(g \approx\) 10 m.s^-2, \(C_x \) = 1,4 et \( \rho \approx\) 1 kg.m^-3. Dans la première partie on avait obtenu une vitesse \( v_{seuil} \approx \) 10 m.s^-1.

Le calcul mène alors à la valeur de la surface minimale de toile : \( \mathbf{S_{min} \approx} \) 25 m².