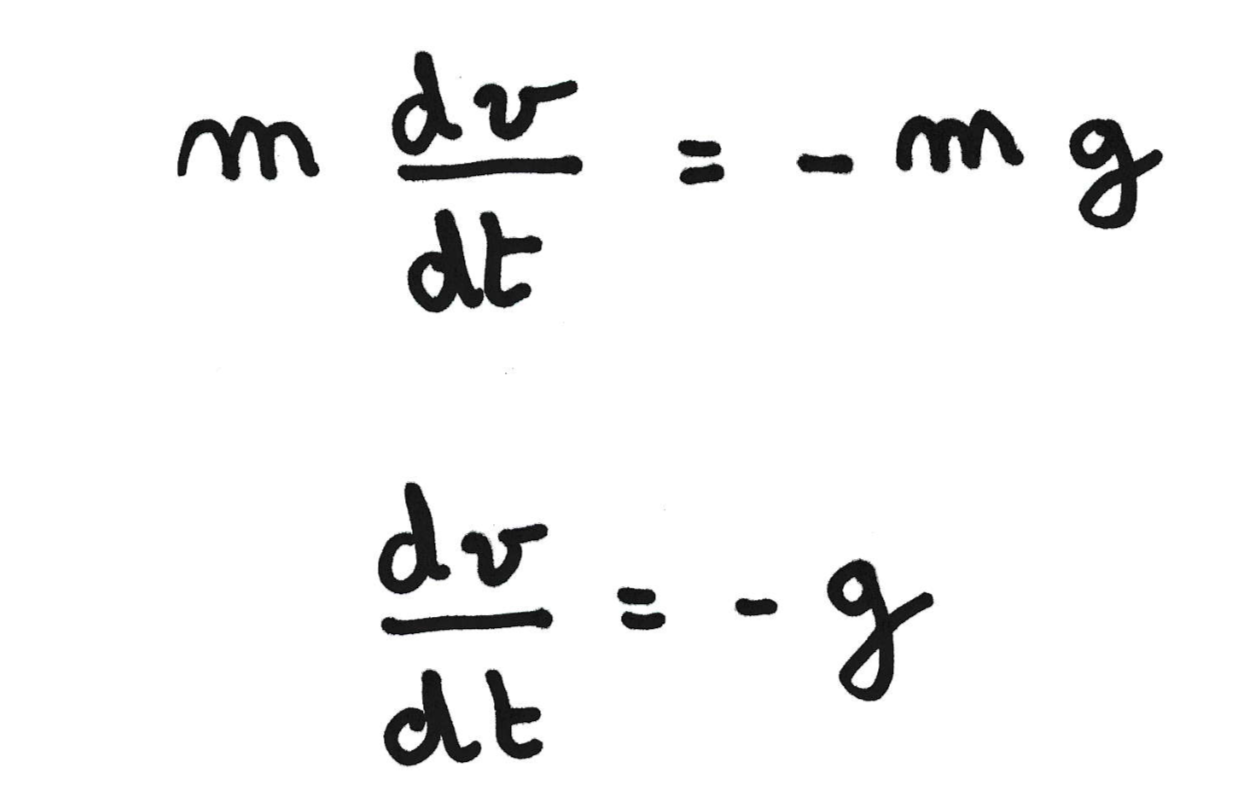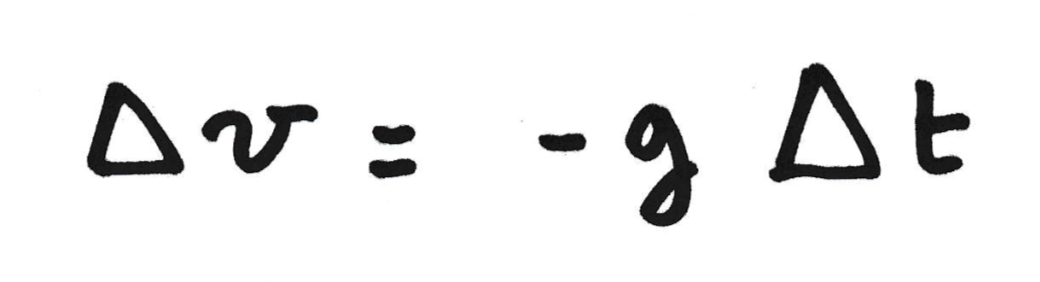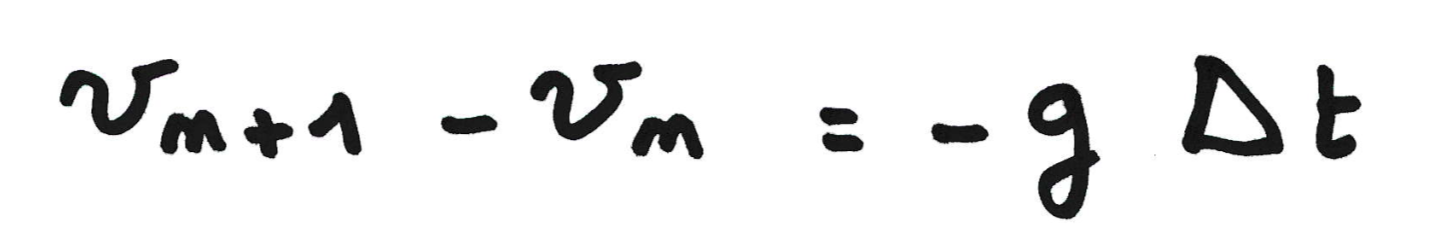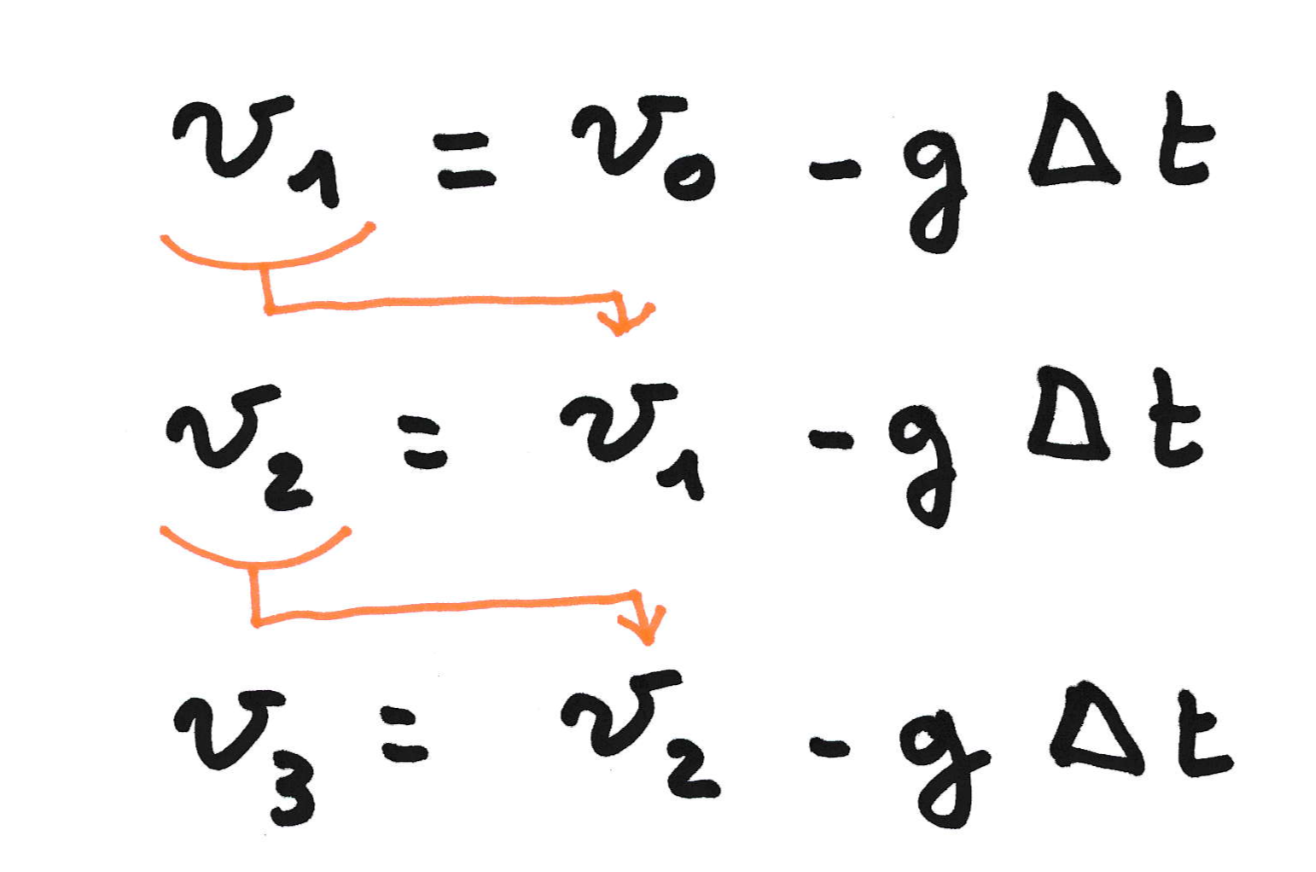Résolution numérique en langage python : la chute libre - 1

Nous lâchons une balle d'une hauteur donnée. Une fois que la balle a quitté la main, la seule force qui s'applique sur elle est la force de gravité (nous négligeons les frottements).

On peut alors écrire le principe fondamental de la dynamique :

En projettant sur l'axe vertical, on obtient :

La masse de l'objet n'intervient pas dans la vitesse de chute.

Nous allons maintenant calculer à chaque instant la position et la vitesse de la balle à l'aide d'une méthode numérique de résolution de l'équation différentielle basée sur le schéma d'Euler, décrit ci-dessous.

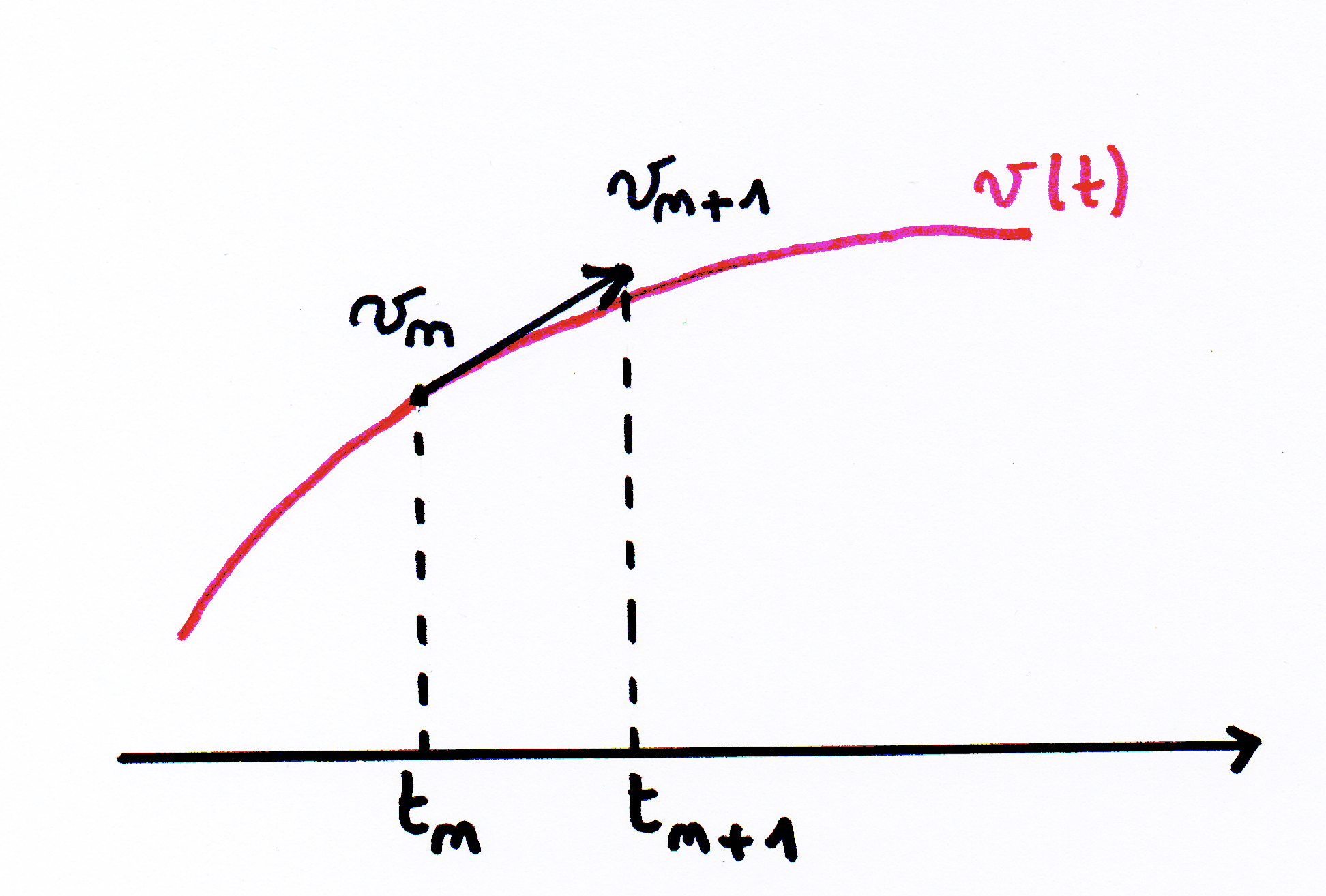
À partir de la connaissance d'une valeur de la vitesse à un instant (v_n à l'instant t_n), on calcule la valeur suivante (v_n+1 à l'instant t_n+1) à l'aide de l'approximation de la dérivée :

Cela se traduit géométriquement par le calcul du coefficient directeur de la tangente à la courbe.

Principe de la méthode d'Euler. Le cas présenté correspond à la méthode d'Euler explicite : le calcul se fait par approximation sur la tangente au point initial (vn).

On remplace donc la dérivée par la valeur de la pente. Une telle approximation n'est raisonnable que si la variation entre les deux instants est toute petite.

Ainsi on peut écrire :

D'où :

On peut maintenant décomposer la variation ∆ entre les deux vitesses correspondant à l'intervalle de temps ∆t :

On a alors :

Ce qui peut s'écrire :

Finalement, il suffit de répéter l'itération afin de connaitre à chaque instant la valeur de la vitesse le long de la chute :

Dans un premier temps, on importe les bibliothèques python nécessaires au traitement des données et à l'affichage des graphiques, figure 1.

Figure 1.  Importation des bibliothèques python utilisées

On renseigne les valeurs de constante (gravitation), paramètre (pas de temps) et données (rayon de la balle de tennis, hauteur du lâché, vitesse initiale), figure 2.

Figure 2.  Initialisation des grandeurs

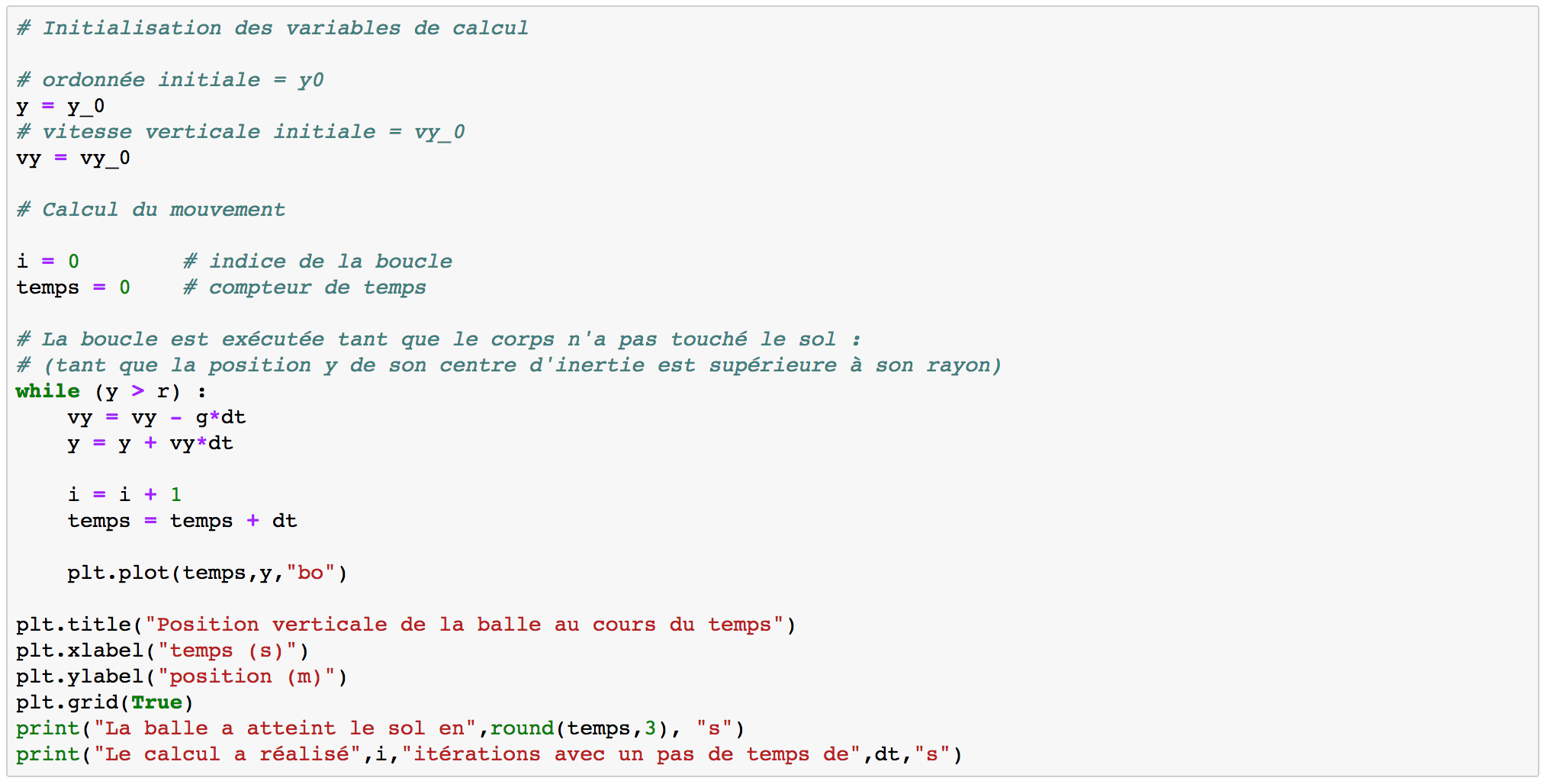
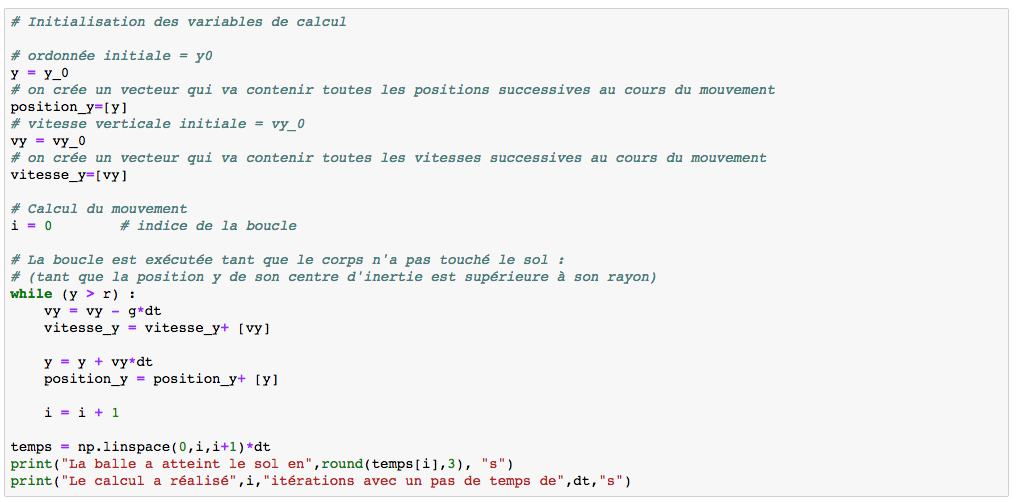
Maintenant, nous appliquons la méthode d'Euler pour coder le mouvement, figure 3.

Figure 3.  Résolution numérique du mouvement de la balle au cours du temps

Dans un premier temps, on initialise la position initiale de la balle à la valeur donnée précédemment (y = y_0) et sa vitesse initiale (vy = vy_0).

Nous introduisons la variable "i" pour compter le nombre d'itérations du calcul le long de la trajectoire. La variable "temps" va nous permettre de mesurer le temps de chute.

Dans cet exemple on s'intéresse à la trajectoire de la balle jusqu'à ce qu'elle touche le sol, on choisit alors d'utiliser une boucle while de la manière suivante :

Tant que le centre d'inertie de la balle est plus haut que son rayon (y > r) (la balle n'a pas touché le sol), on calcule, pour chaque itération, sa vitesse et sa position, on incrémente le compteur i de 1 et le compteur temps d'un pas de temps. On trace un nouveau point y de la trajectoire.

Boucle while

Attention !

• Lorsqu'on introduit la boucle while, ne pas oublier le signe ":" après la condition.
• Les instructions répétées dans la boucle doivent être indentées (tabulation).

Dans cet exemple, seules les instructions suivantes sont répétées à chaque itération.

Lorsque l'on sort de la boucle, figure 3, (les dernières instructions ne sont pas indentées sur la boucle while), on ajoute à la représentation graphique : un titre, les grandeurs et unités des axes, et un quadrillage.

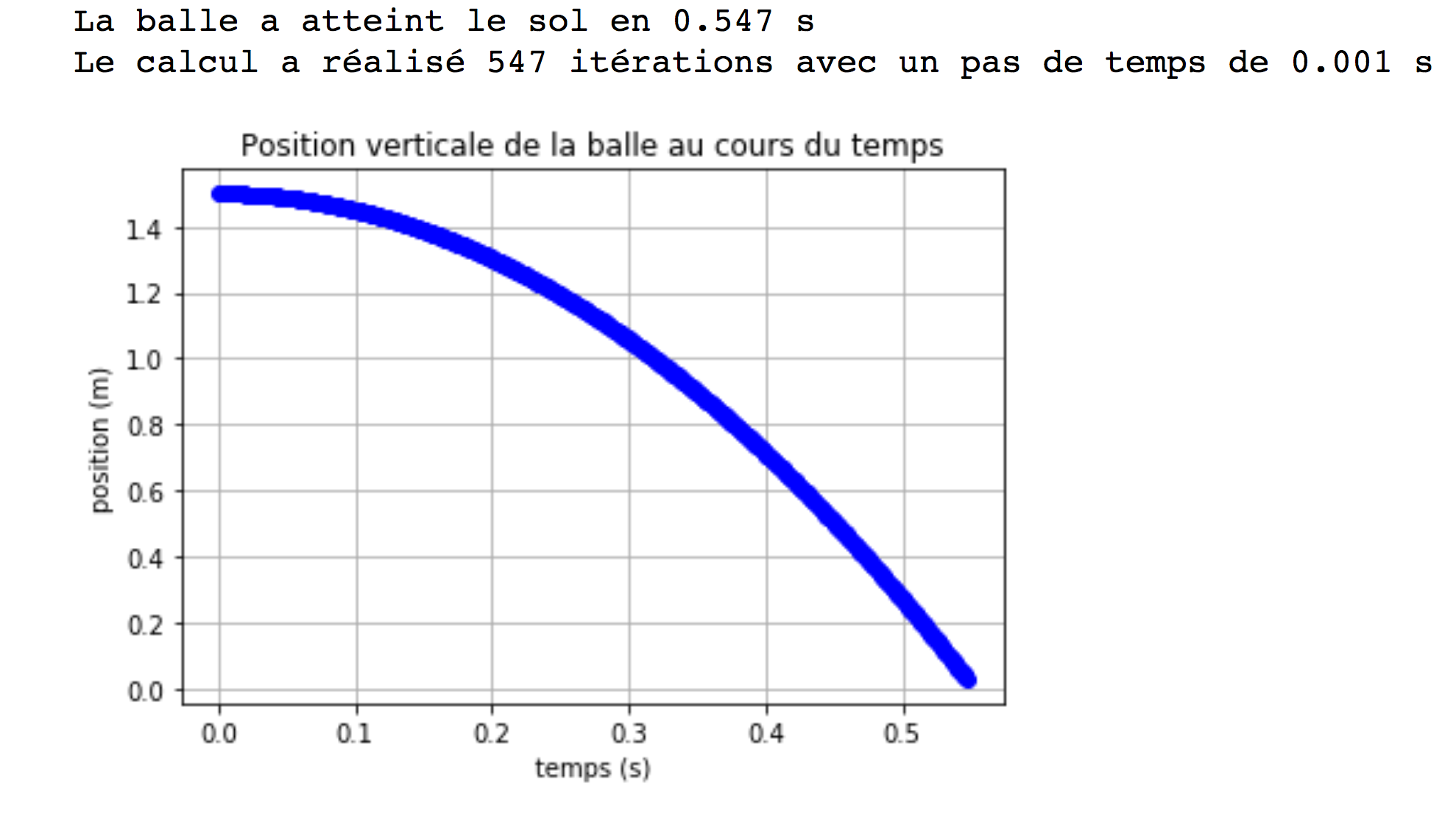
À l'aide de la fonction print, on affiche le temps de chute de la balle. La fonction round(x,3) renvoie la valeur de x arrondie à 3 décimales. On affiche de nombre d'itérations du calcul et le pas de temps.

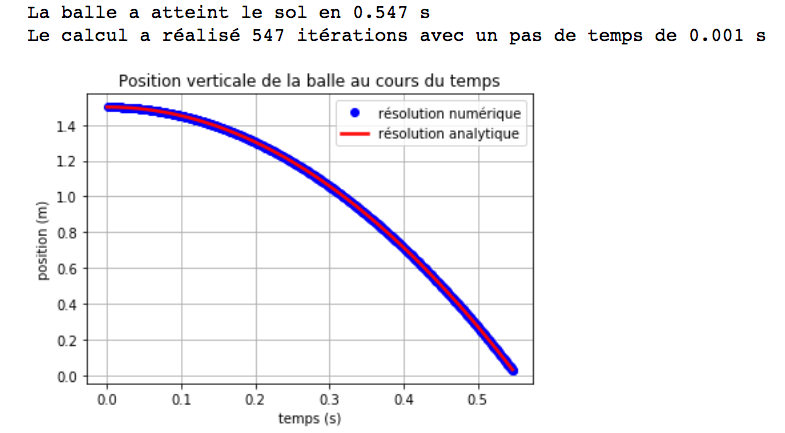
Le code renvoie le graphique et les éléments suivants, figure 4.

Figure 4.  Représentation graphique de la trajectoire de la balle au cours du temps

L'hypothèse de départ de cette modélisation est de confondre une dérivée avec un ∆. Cela signifie que, pour être au plus juste, il est nécessaire de choisir un pas de temps très petit, de telle façon qu'entre deux pas, il n'y ait qu'une toute petite variation des grandeurs.

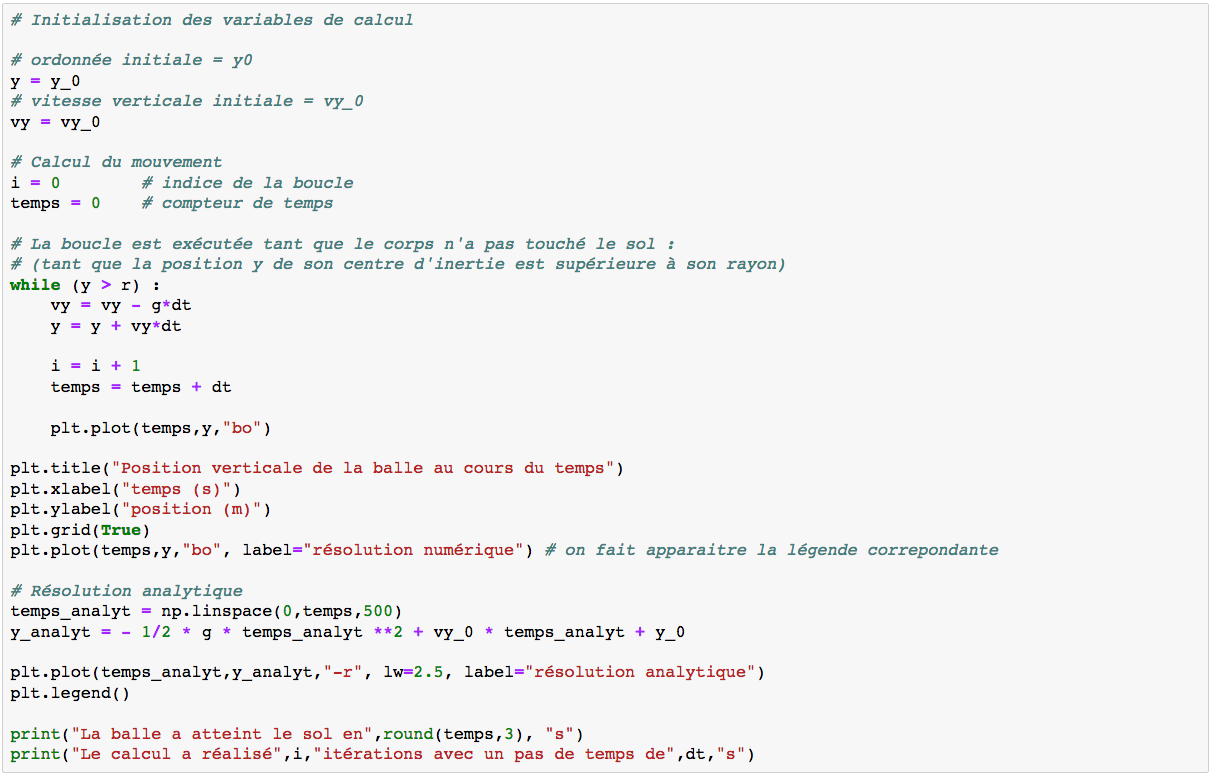
Pour tester notre méthode de résolution numérique, on propose de tracer sur le même graphe, le résultat analytique du problème : y(t) = 1/2gt² + vy₀t + y₀

Nous avons besoin de créer deux vecteurs : "temps_analyt" correspondant aux abcsisses et "y_analyt" correspondant aux ordonnées. La création du vecteur est réalisée à l'aide de la fonction linspace, de la manière suivante :

Définition d'un vecteur (linspace) partant de la valeur de temps minimum (0), à la valeur maximum (temps), contenant 500 points (500).

Le vecteur correspondant à la trajectoire "y_analyt" est donné par l'équation de la trajectoire.

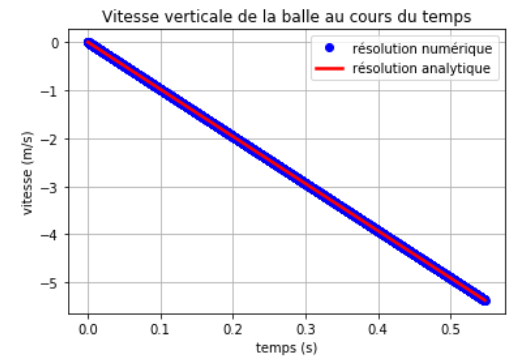
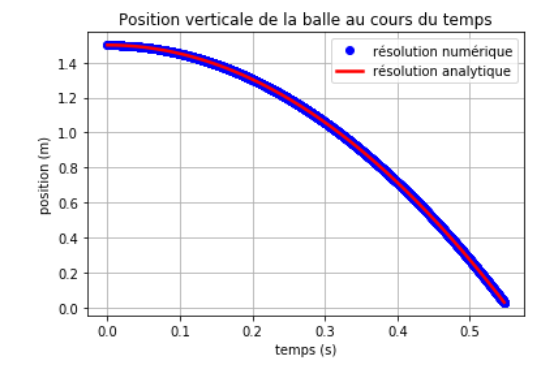
On trace le résultat analytique avec une ligne rouge (-r) assez épaisse (lw=2.5). On ajoute une légende (label) pour chaque courbe, l'affichage est géré par la fonction plt.legend(), figure 5.

Figure 5.  Code python du calcul de la trajectoire de la balle en chute libre

Le programme affiche le graphique, figure 6.

Figure 6.  Représentation graphique du calcul numérique (bleu) et du résultat analytique (rouge) de la trajectoire de la balle en chute libre

Le calcul de la trajectoire par la méthode numérique suit complètement le résultat analytique.

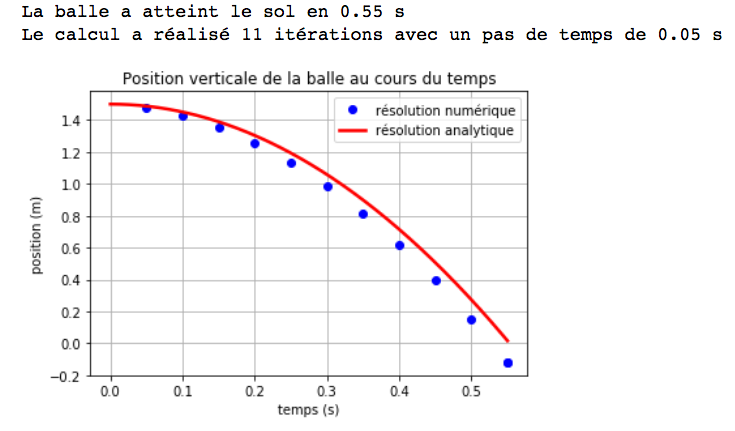
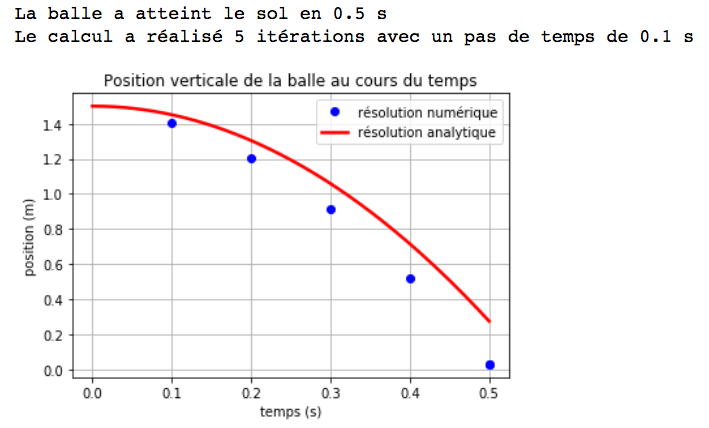
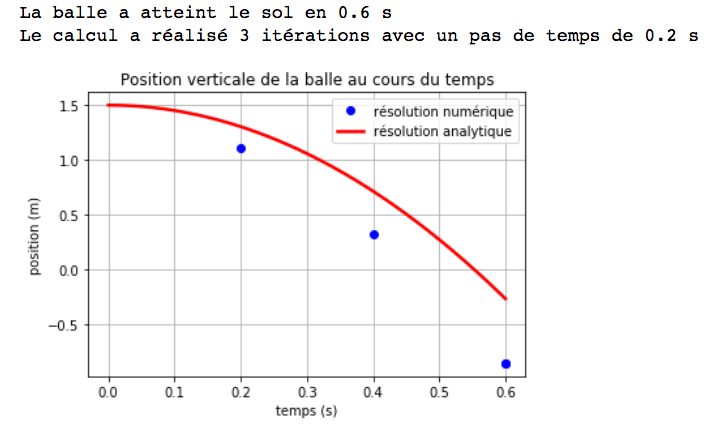
Maintenant, observons les effets du choix du pas de temps sur la méthode de résolution, tableau 1.

Nous augmentons successivement la valeur du pas de temps à 10 ms; 50 ms; 100 ms et 200 ms.

Tableau 1.  Mise en évidence de la précision du calcul lors de la résolution numérique

Pas de temps dt = 0,01 s	Pas de temps dt = 0,05 s
Pas de temps dt = 0,1 s	Pas de temps dt = 0,2 s

On constate que le modèle s'écarte de plus en plus de la trajectoire réelle. Dans certains cas, le programme renvoie une position y négative de la balle. Les pas de temps sont effectivement trop grands et ne respectent plus la condition initiale de toutes petites variations.

Nous avons pu vérifier qu'il est donc nécessaire de choisir un pas de temps très petit, de façon à pouvoir remplacer une dérivée avec un ∆.