Activer le mode zen
Ressource au format PDF
Mots-clés
Classification
La Terre est « ronde »
13/03/2019
Résumé
Cet article répond à la question : Pourquoi la Terre est sphérique (parce que les montagnes ne peuvent pas être trop hautes) et donne la définition du rayon critique de sphéricité des astres. Il traite aussi de sismologie et met en évidence la sphéricité des enveloppes internes de la Terre.
Table des matières
Transcription par Daphné Lemasquerier et Frédéric Chambat de la présentation de Frédéric Chambat du 14 septembre 2015 à l'ENS de Lyon, donnée dans le cadre du cours pluridisciplinaire des écoles doctorales EPIC, PHAST et INFOMATH intitulé La Terre, sa forme, sa rotation, ses marées - Morceaux choisis mathématiques, géophysiques et historiques.
1. Hauteur maximale des montagnes
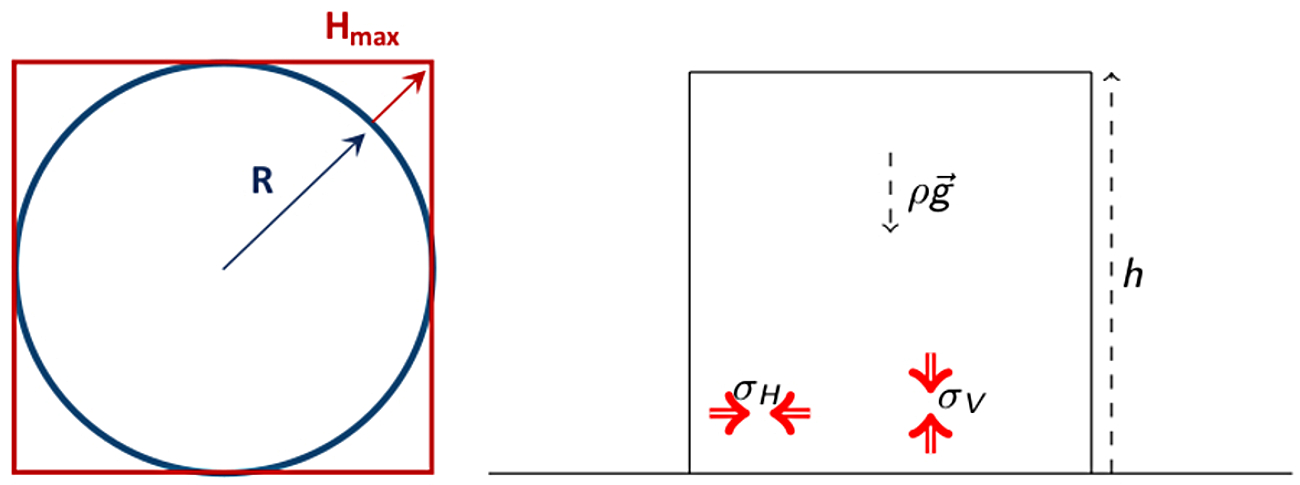
Qu'est-ce qu'une planète qui ne serait pas sphérique ? Une réponse pourrait être : ce serait une sphère avec de très grosses montagnes. Un cube par exemple, comme sur la figure 1 (gauche). On peut alors définir un critère de rotondité : on dit que la planète est sphérique si la hauteur maximale des montagnes hmax est petite devant le rayon de la planète R.
Le questionnement à propos de la rotondité de la Terre peut être reformulé de la manière suivante : pourquoi et par quoi la taille des montagnes sur Terre est-elle limitée ?
Pour répondre à cette question, faisons appel à la mécanique des milieux continus, et plus particulièrement à la notion de contraintes dans un matériau donné. Une contrainte représente une force par unité de surface, en dimension elle est donc assimilable à une pression, mais elle est plus générale que la pression : sur un élément de surface dans un matériau, une contrainte s'exerce à priori dans n'importe quelle direction de l'espace (et non pas forcément perpendiculairement comme la pression). De plus, la contrainte dépend de la direction de la surface considérée.
Dans le cas d'une montagne (très) simple de hauteur h (figure 1, à droite) soumise à son poids (force volumique ), on peut considérer qu'il existe une contrainte qui s'exerce verticalement (sur les éléments de surface horizontaux) et une autre qui s'exerce horizontalement (sur les éléments de surface verticaux). La première, par intégration sur une colonne, vaut σV = ρgh, alors que la seconde est nulle : σH = 0, puisque celle-ci correspond à la pression exercée par l'atmosphère sur les côtés, qui est négligeable.
Le déviateur des contraintes, qui mesure les différences entre les contraintes principales, s'exprime alors simplement comme τ = σV − σH = ρgh.
Figure 1. Planète et montagne À gauche : une planète sphérique de rayon R et une planète non-sphérique. Nous appelons ici “montagne” la différence entre les deux. La hauteur maximale des montagnes est notée hmax. À droite : schéma d'une montagne de hauteur h, la gravité est notée , et les contraintes horizontales σH et verticales σV. |
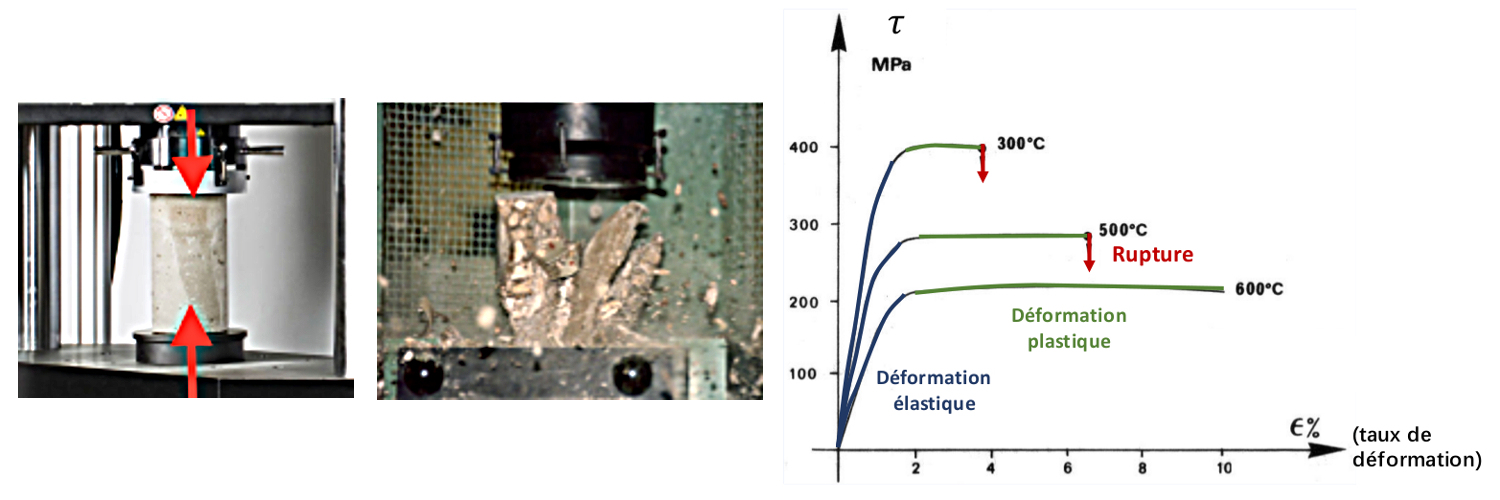
Ces contraintes dans la montagne sont celles qui règnent dans une carotte de roche soumise à une contrainte σV sur les deux bords opposés. Il en résulte, au fur et à mesure que la contrainte augmente, une déformation d'abord élastique, puis “ductile”, résultant de processus de fluage, puis une déformation cassante (figure 2).
Figure 2. Exemple de réponse d'un matériau naturel à une contrainte On voit à la fois une déformation ductile (pli) et cassante (faille). Il s'agit ici du pli-faille de Saint-Rambert en Bugey. |
La figure 3 montre les résultats d'expériences de confinement de carottes de roches visant à mesurer cette relation entre la contrainte appliquée et la déformation résultante.
Figure 3. Expérience de compression d'une carotte de roche À gauche : déformation élastique. Au milieu : rupture. À droite : contrainte τ en fonction du taux de déformation ε. Dans le domaine élastique, la contrainte est proportionnelle à la déformation. Dans le domaine plastique, pour une contrainte maintenue constante, la déformation se poursuit jusqu'à fracture. Les seuils dépendent de la température. En deçà d'une certaine température, le domaine plastique disparaît. Les plis observés en surface n'ont pas pu se former à température “ambiante”, ils résultent de contraintes subies anciennement en profondeur et à plus haute température. |
Ces expériences montrent que la rupture des roches classiques de la croûte intervient entre 100 et 500 MPa (Fossen, 2010 [2]). Pour mener un calcul d'ordre de grandeur, prenons une contrainte maximale égale à τmax = 300 MPa. Or la contrainte à la base d'une montagne augmente avec sa hauteur. La hauteur d'une montagne est donc limitée et son maximum, qu'on notera hmax, est donné par la contrainte de rupture, c'est-à-dire par la relation τmax = ρghmax. En prenant ρ = 3000 kg.m−3 (ordre de grandeur de la masse volumique de la croûte terrestre continentale) et g = 10 ms−2, il vient hmax = 10 km. Cet ordre de grandeur correspond bien à ce qu'on observe sur Terre : la hauteur d'Hawaï, plus haute montagne isolée, est de 9 km (5 km immergés et 4 km émergés).
Pour Mars, où la gravité est de g = 3,6 ms−2, on obtient ainsi une hauteur maximale des montagnes de 28 km, ce qui correspond là encore aux observations, le Mont Olympe (Olympus Mons) a 27 km d'altitude. Pour ces deux planètes, et pour celles où la gravité est suffisante, la hauteur des montagnes est donc une toute petite fraction de leur rayon : on peut considérer qu'elles sont sphériques.
2. Rayon critique pour qu'une planète soit sphérique
Lorsque la gravité est plus faible, c'est-à-dire pour une plus petite planète, la hauteur maximale des montagnes est plus grande, et peut théoriquement devenir comparable au rayon. Déterminons donc un rayon critique correspondant.
En notant G la constante de gravitation universelle, M la masse du corps considéré, sa densité moyenne, R son rayon, la gravité est, en ordre de grandeur :
- .
Prenons par exemple comme critère de sphéricité hmax ≤ R/4, et notons Rc le rayon critique pour lequel l'égalité τmax = ρghmax est satisfaite. Avec l'expression de g précedente, on trouve alors :
- .
Pour les petits corps, , si bien que Rc ≈ 700 km. On en conclut qu'au-delà de quelques centaines de kilomètres, un corps céleste auto-gravitant, non tournant, est (approximativement) sphérique.
En dessous de quelques centaines de kilomètres on ne peut rien dire : les corps peuvent être quelconques (dont sphériques). Ce résultat est cohérent avec quelques formes d'astéroïdes connus (figure 4) : le plus gros d'entre eux est sphérique alors que les autres ont parfois des formes éloignées de la sphère.
Figure 4. Exemples d'astéroïdes de formes et de tailles variées En haut à gauche, Cérès, le plus gros des astéroïdes, a un rayon de quasiment 500 km et est donc proche de la sphéricité. Pour cette raison, selon la nouvelle nomenclature astronomique, il n'est plus qualifié d'astéroïde mais de planète naine. À droite, le petit astéroïde Éros a une forme irrégulière. Au milieu, le cas intermédiaire de Vesta, plus irrégulier que Cérès mais moins qu'Éros. En bas, Camilla, l'un des plus gros astéroïde. Il n'a pas été survolé de près, c'est pourquoi sa forme est peu précisément connue. Elle est déduite des mesures de luminosité depuis la Terre. On voit toutefois que Camilla n'est probablement pas sphérique. |
3. L'intérieur de la Terre est-il sphérique ?
3.1 Une symétrie sphérique interne
Nous avons expliqué pourquoi la surface de la Terre est sphérique, qu'en est-il de ses couches internes ?
On peut commencer par répondre à cette question de façon théorique. En écrivant les équations de la mécanique et en faisant quelques hypothèses, on montre qu’à une interface entre deux couches, le saut de contrainte généré par ce relief est proportionnel à la gravité, à la hauteur de la topographie, et au saut de densité́ entre les deux couches. On a alors [τ] = [σV − σH] = [ρ]gh, en notant entre crochets [] les sauts à l'interface. À partir de là, il est facile de montrer que la hauteur des reliefs est limitée. L'intérieur de la Terre devrait donc aussi être à symétrie sphérique. Voyons ce que les observations nous en disent.
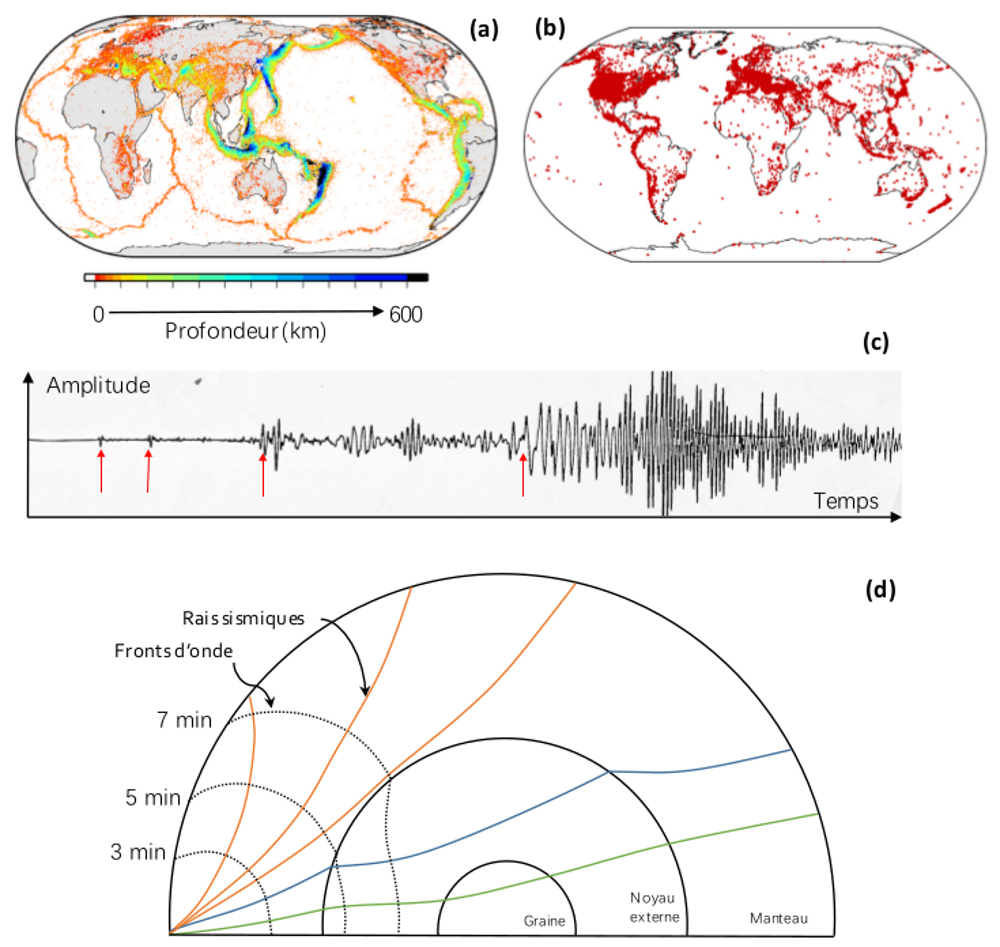
Les nombreuses données de la sismologie sont de précieux outils pour étudier la structure interne de la Terre (figure 5). On peut par exemple mesurer le temps de propagation des ondes sismiques du foyer à une station sismique.
Figure 5. Séismes, stations sismiques et propagation des ondes sismiques (a) Hypocentres des séismes enregistrés par l'International Seismological Centre (ISC) de 1960 à 2015 colorés suivant leur profondeur (de rouge pour les plus superficiels à bleu et noir pour les plus profonds. (b) Les 22 000 stations sismiques de l'ISC. (c) Sismogramme enregistré par une station du réseau geoscope lors d'un important séisme de 1989 (ici déplacement longitudinal). Les flèches rouges indiquent l'arrivée de différents types d'ondes (ondes de volume P puis S et ondes de surface). (d) Représentation schématique de la propagation d'ondes sismiques P dans la Terre. |
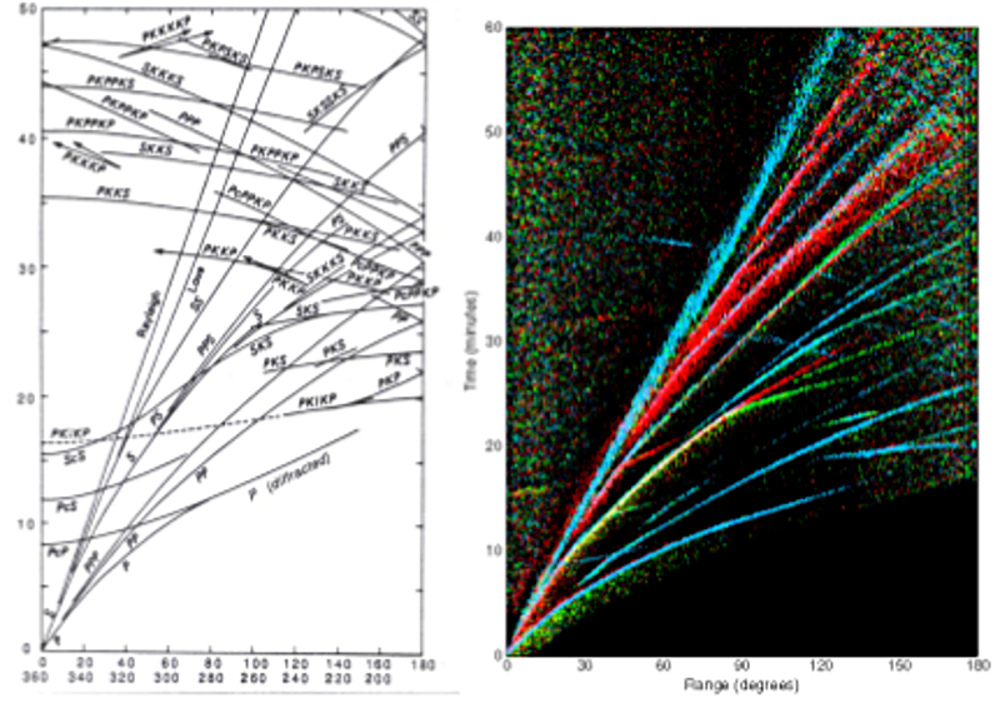
En combinant l'ensemble des mesures obtenues sur Terre, et en les reportant en fonction de la distance épicentrale (on appelle ces graphiques des hodochrones), on obtient la figure 6 (à droite). Pour un même type d'onde, les points d'une hodochrone forment une courbe fine et non une ligne très épaisse, ce qui signifie que tous les couples séisme-station à une distance donnée voient un sous-sol identique où qu'ils soient. C'est d'ailleurs le cas sur la figure 6 de gauche obtenue, justement, en modélisant la propagation des ondes sismiques en supposant la sphéricité. L'observation synthétisée dans la figure de droite atteste donc de la sphéricité interne de la Terre.
Figure 6. Hodochrones théoriques et réelles montrant la sphéricité des interfaces internes de la Terre À gauche, hodochrones théoriques (temps d'arrivée en fonction des distances épicentrales) obtenues à partir d'un modèle de Terre à symétrie sphérique. Les différents sigles désignent différents types d'onde selon le trajet qu'elles ont parcouru (on distingue les ondes qui ont traversé le noyau ou non, celles qui sont engendrées par réfraction, celles qui se sont réfléchies). À droite, hodochrones obtenues à partir de données réelles : combinaison des données de 33 000 sismogrammes enregistrés lors de séismes de magnitude supérieure à 5. Chaque point est un temps de parcours mesuré. Sont représentées les composantes verticale (bleu), longitudinale (vert) et transverse (rouge) du déplacement (Astiz et al., 1996 [1]). |
3.2 Exemples de mesures d'écart à la sphéricité (tomographie sismique)
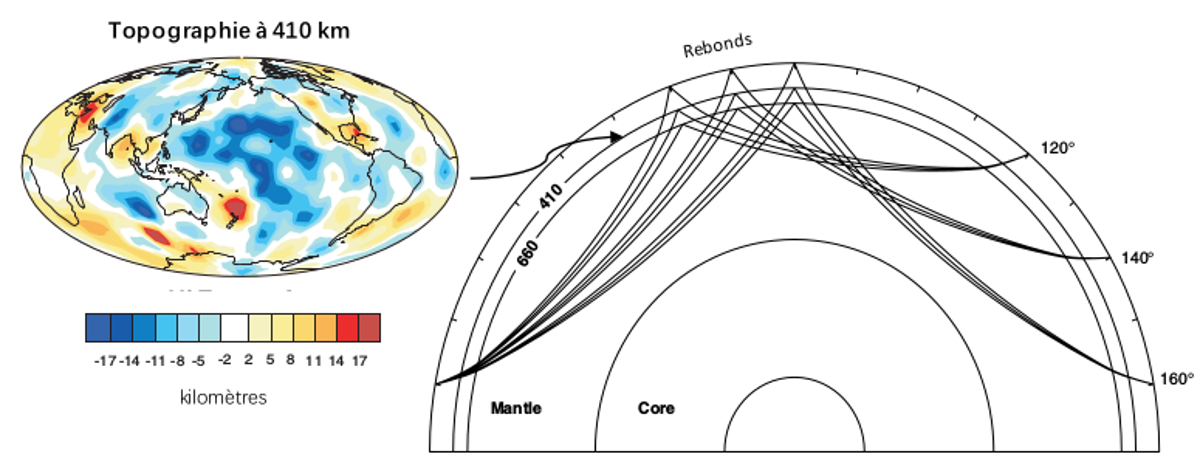
Sphéricité d'interfaces. En étudiant cette fois les temps d'arrivée des ondes sismiques dans l'épaisseur du trait de la figure 6 (droite), on peut établir des cartes de la topographie d'une interface en profondeur. En mesurant la différence de temps d'arrivée entre l'onde réfléchie à la surface et l'onde réfléchie à la discontinuité (par exemple figure 7), on peut en déduire la distance entre la surface et cette discontinuité, et donc sa topographie. Par exemple, Houser et al. (2008 [3]) ont déterminé la topographie de l'interface située autour de 410 km de profondeur (surface supérieure de la zone dite de transition). On voit sur la carte obtenue un faible écart à la sphéricité (écarts inférieurs à 20 km).
Source - © 2008 D'après Houser et al. [3] À gauche : topographie de l'interface située à une profondeur de 410 km. Les variations sont de ±20 km. À droite : schéma de principe des mesures. On fait la différence entre les temps des parcours des ondes qui ont rebondi à la surface de la Terre et celles qui ont rebondi sous l'interface étudiée. |
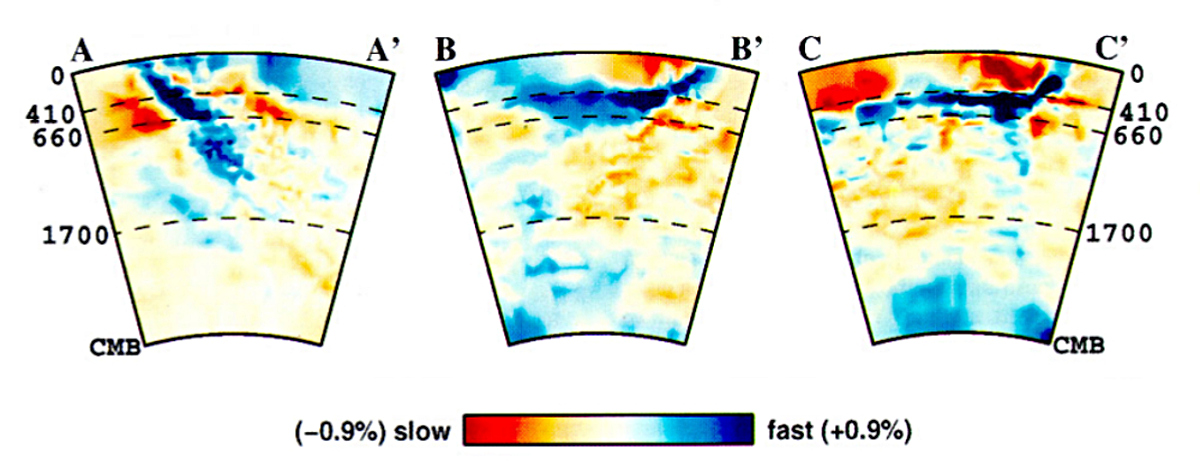
Entre deux interfaces. La sismologie permet également de quantifier les variations latérales de vitesses sismiques entre deux interfaces. Cette méthode consiste à analyser les variations de temps d'arrivée des ondes pour en déduire où elles sont accélérées ou ralenties, et éventuellement interpréter cela en terme de densité et de température des zones traversées par les ondes. À partir de multiples mesures, on peut ainsi reconstituer un profil de variation de vitesse des ondes sismiques au sein du manteau. On voit par exemple sur les profils de la figure 8 que ces variations latérales relatives de vitesses sont de l'ordre de 1 %, ce qui est faible.
Source - © 2000 D'après Kárason et van der Hilst [4] Profils au niveau, de gauche à droite, (AA') de la mer d'Égée, (BB') des îles Kouriles, (CC') de la fosse d'Izu-Bonin. Ces trois profils sont localisés au niveau de zones de subduction, et montrent des anomalies de vitesse rapides associées aux plaques plongeantes. Dans la première coupe, la plaque subduite traverse la zone de transition, alors que dans les deux autres elle y stagne. |
4. Conclusion : modèle moyen de Terre
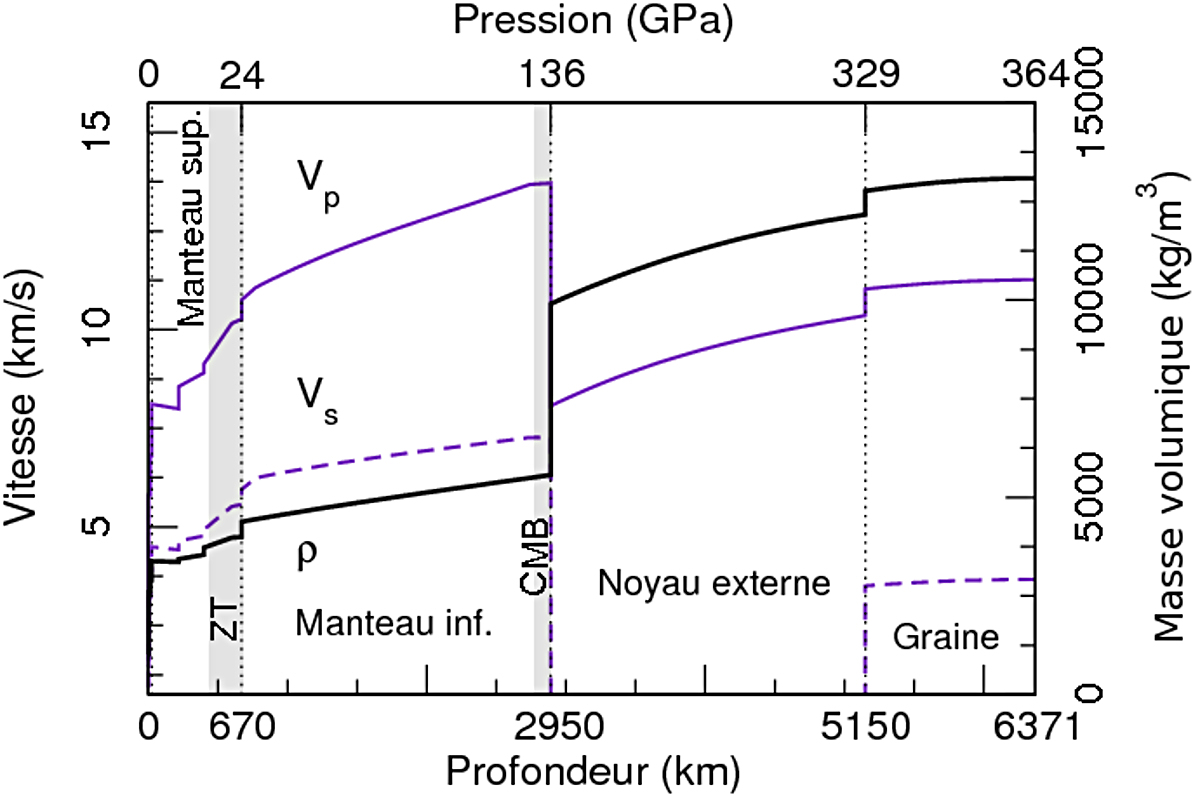
Ainsi, en première approximation, à l'ordre du pour cent près, la Terre est à symétrie sphérique, en surface et à l'intérieur. La sismologie a permis de proposer des modèles sphériques de Terre, qui la représentent en couches concentriques où la vitesse des ondes et la densité varient de manière lisse, séparées par des discontinuités de ces paramètres. L'un de ces modèles est PREM (Preliminary Reference Earth Model, figure 9).
Mais, en seconde approximation, la Terre n'est pas parfaitement ronde. Ce modèle est déformé sous la forme d'un ellipsoïde un peu aplati aux pôles, ce sera l'objet du prochain article La Terre est un peu aplatie : comment Newton calcule l'aplatissement « sans sortir de chez lui ».
Figure 9. Modèle PREM de structure interne sphérique de la Terre Variations des vitesses des ondes sismiques P et S, et de la densité en fonction de la profondeur. Entre deux interfaces, les paramètres sont supposés varier de façon lisse. |
5. Pistes d'exploitation
6. Les autres articles du dossier La Terre, sa forme, sa taille, sa rotation :
- La Terre est ronde ! Ératosthène et la mesure du rayon terrestre
- Les mesures de méridien vont-elles confirmer la théorie de Newton ?
- La Terre ellipsoïde ? Les mesures de la gravité au XVIIIème siècle
- Clairaut et sa bande, l'expédition de Clairaut et Maupertuis en Laponie
- La Terre tourne... Le gyroscope de Foucault
- Les machines de lord Kelvin
- Les marées depuis Newton
- La Terre est un peu aplatie : comment Newton calcule l’aplatissement « sans sortir de chez lui »
Bibliographie
L. Astiz, P. Earle, P. Shearer, 1996. Global stacking of broadband seismograms, Seismological Research Letters, 67, 4, 8-18
H. Fossen, 2010. Structural geology, Cambridge University Press, 480p
C. Houser, G. Masters, M. Flanagan, P. Shearer, 2008. Determination and analysis of long-wavelength transition zone structure using SS precursors, Geophysical Journal International, 174, 1, 178-194 [pdf]
H. Kárason, R.D. van der Hilst, 2000. Constraints on mantle convection from seismic tomography, in The history and dynamics of global plate motions, Geophysical Monograph, 121, 277–288
Pour citer cet article :
La Terre est “ronde”, Frédéric Chambat, Daphné Lemasquerier, mars 2019. CultureSciences Physique - ISSN 2554-876X, https://culturesciencesphysique.ens-lyon.fr/ressource/Terre-spherique.xml