Activer le mode zen
Ressource au format PDF
Mots-clés
Classification
Force de marée et déformation de la Terre
06/04/2015
Résumé
Ordre de grandeur et profil d'équilibre de la déformation due à la force de marée pour une Terre homogène.
Table des matières
Ordre de grandeur de la déformation terrestre
Une fois la force de marée calculée, comment déterminer la déformation de la Terre ? Une première approche est de chercher un ordre de grandeur. Pour cela, on suppose la Terre sphérique et on commence par remarquer que la force de marée a la dimension d'une pesanteur. Le problème compte cinq variables : le rayon de la Terre , la distance Terre-Lune , le déplacement de la surface au plus haut du bourrelet sous l'effet combinée de la force de marée et de la gravité de la Terre sphérique. Ces variables comptent deux dimensions : les distances et la pesanteur. Il y a donc trois nombres sans dimensions indépendants, par exemple, , et , et l'équation physique qui exprime le lien entre les variables peut s'écrire :
- .
Cette méthode, dimensionnelle, est formalisée sous le nom de théorème Π ou théorème de Vaschy-Buckingham[1].
Pour aller plus loin, on peut se placer dans le cadre d'une théorie linéaire de la déformation, élastique ou fluide. Cela exprime le fait que la déformation est proportionnelle à la force appliquée (d'ailleurs, on ne voit pas en quoi la distance interviendrait autrement que dans la force de marée). Au final on a donc un ordre de grandeur :
- ,
où est un autre nombre sans dimension[2] :
- .[3]
Avec , d=384 000 km, , on trouve et . Avec le même raisonnement pour le Soleil et avec des notations évidentes : , ; on trouve alors c'est-à-dire et . L'influence solaire n'est pas négligeable quoique inférieure à celle de la Lune. Lorsque les trois astres sont alignés (tous les 14,75 jours) les forces de marées lunaire et solaire s'ajoutent, on a alors de grandes marées qu'on appelle vives-eaux ; quand les astres sont en quadrature les marées sont faibles, ce sont les mortes-eaux.
Un profil d'équilibre oblong
Quel est le profil de la Terre déformée ?
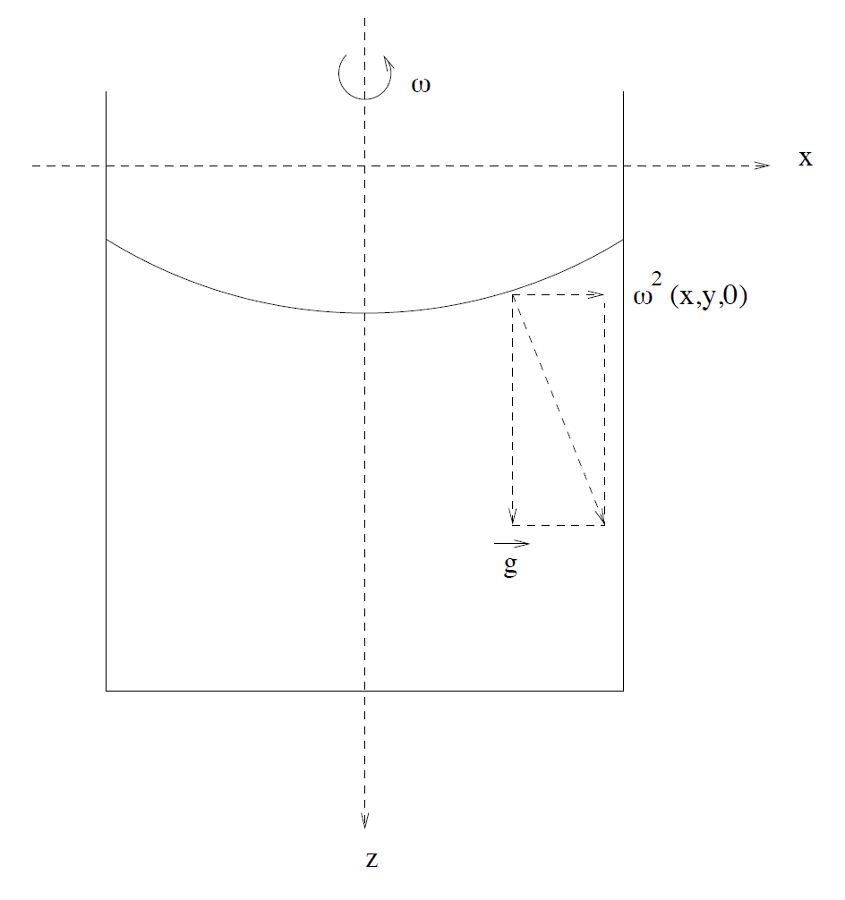
Rappelons-nous l'expérience du récipient rempli d'un fluide parfait. Au repos, la surface du fluide est plane et horizontale : elle est perpendiculaire à la pesanteur . Lorsqu'on le fait tourner à vitesse angulaire constante autour de son axe (cf. figure ci-dessous) et qu'on suppose que le fluide tourne d'un seul bloc, la surface prend une forme parabolique. En effet, la surface est perpendiculaire, cette fois, à la somme des deux forces, de pesanteur et centrifuge, c'est-à-dire à . Pour poursuivre le calcul, le physicien dispose alors d'un outil redoutable : le potentiel. En effet cette force "dérive" d'un potentiel, c'est-à-dire qu'elle s'écrit . Le gradient étant perpendiculaire au potentiel, les surfaces perpendiculaires à la force sont donc des surfaces équipotentielles. La surface libre du liquide a donc pour équation .
Figure 1. Récipient de liquide tournant autour de son axe à vitesse ω
La forme de la surface du liquide en rotation est une parabole.
Procédons au même raisonnement pour la surface de la Terre et supposons que la surface est un fluide parfait qui tourne en bloc autour de l'axe des pôles. La surface du fluide est alors celle pour laquelle la somme de la pesanteur et de l'accélération de marée est perpendiculaire à la surface. C'est donc aussi, comme pour l'exemple du récipient, la surface pour laquelle la somme du potentiel de pesanteur et du potentiel de marée est constante. On trouve alors que le potentiel de pesanteur aplatit la Terre aux pôles, avec une différence des rayons équatoriaux et polaires de 21 km[4]. Le potentiel de marée (, voir la définition du potentiel de marée dans le chapitre précédent) allonge lui la Terre dans la direction de la Lune mais d'une quantité beaucoup plus petite. On trouve en effet que cet allongement s'exprime par :
- ,
avec le maximum, dans la direction Terre-Lune, qui vaut :
- ,
et , l'angle entre TM et TL.
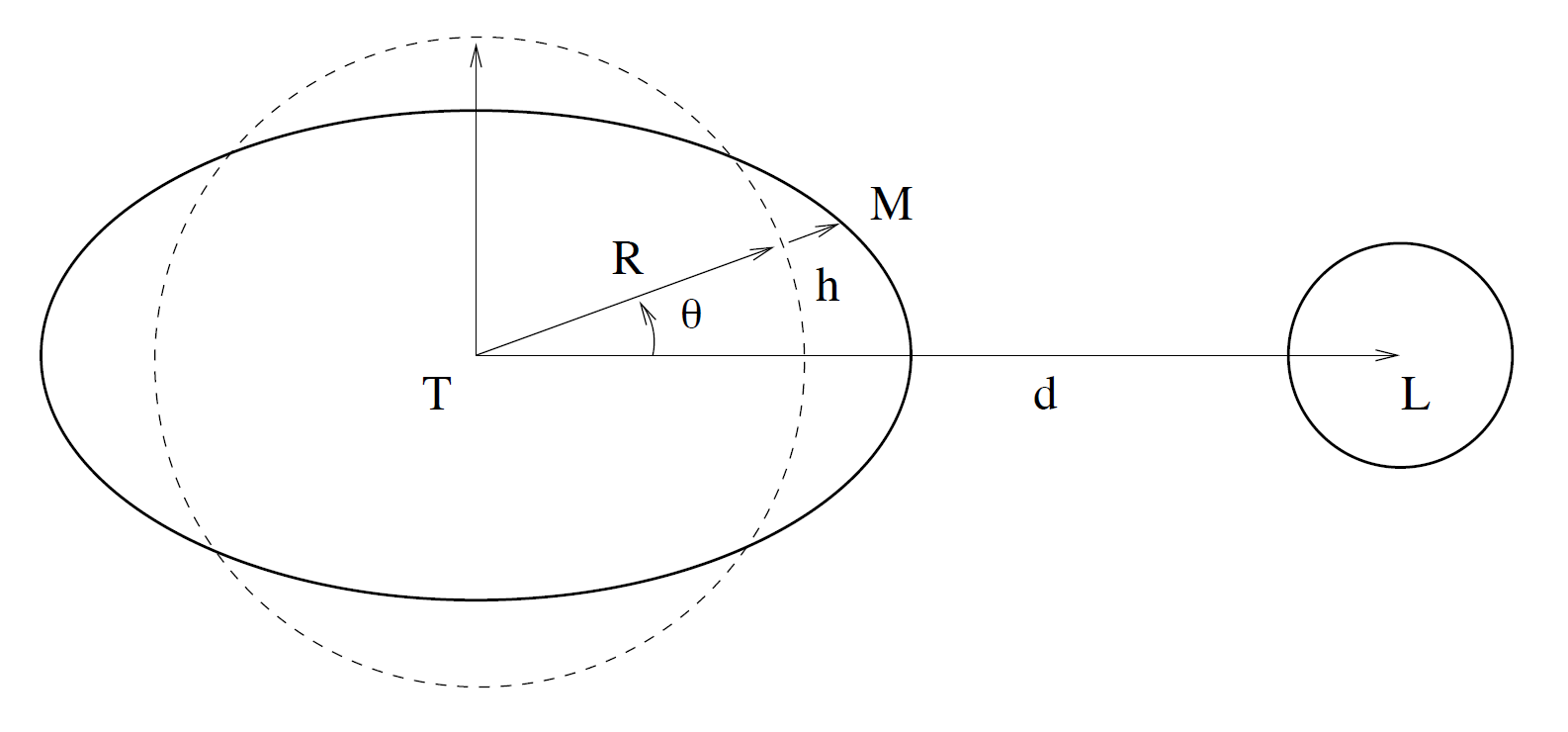
Suivant cette théorie, la Terre fluide se soulève de 36 cm dans la direction de la Lune () et s'abaisse de 18 cm dans le plan perpendiculaire passant par le centre de la Terre (). La forme générale est ce que les mathématiciens appellent un ellipsoïde allongé, ou oblong, dans la direction de la Lune, une sorte de ballon de rugby en moins pointu (cf. figure ci-dessous).
Figure 2. Forme oblongue de l'équipotentielle de marée
La forme de l'équipotentielle est donnée par l'équation polaire :.
Dans la réalité, on observe en fait que le déplacement moyen des continents est de l'ordre de 30 cm, alors qu'il est très variable dans les océans, de 0 à 1 mètre en plein océan, et jusqu'à plusieurs mètres sur certaines côtes. De plus, si la déformation des continents prend bien la forme du ballon de rugby, celle des océans est beaucoup plus complexe. La suite de cet exposé nous permettra de comprendre les raisons de ces différences. Pour cela nous allons commencer par parler des marées de la Terre solide, les plus simples, puis nous en viendrons aux marées océaniques.
Plan de l'exposé
Cinq notes constituent cet exposé sur les marées :
Une partie de cet ensemble de notes sur les marées reprend des articles rédigés avec Étienne Ghys pour le site internet des Mathématiques pour la Terre – 2013.
Pour citer cet article :
Force de marée et déformation de la Terre, Frédéric Chambat, avril 2015. CultureSciences Physique - ISSN 2554-876X, https://culturesciencesphysique.ens-lyon.fr/ressource/maree-deformation.xml