Activer le mode zen
Ressource au format PDF
Mots-clés
Classification
La Terre ellipsoïde ? Les mesures de la gravité au XVIIIe siècle
01/06/2018
Résumé
Les mesures de pesanteur et de distances qui ont permis d'attester l'aplatissement de la Terre selon son axe de rotation (Terre ellipsoïdale aplatie aux pôles).
Table des matières
Transcription par Cyril Langlois de la présentation d'Hugues Chabot du 28 septembre 2015 à l'ENS de Lyon, donnée dans le cadre du cours pluridisciplinaire des écoles doctorales EPIC, PHAST et INFOMATH intitulé La Terre, sa forme, sa rotation, ses marées - Morceaux choisis mathématiques, géophysiques et historiques.
1. Les mesures de l'arc de méridien Paris-Amiens
La théorie de la gravitation de Newton n'a été acceptée qu'avec des réserves par les communautés scientifiques occidentales. En France, c'est grâce à la traduction des Principia mathematica (1687) de Newton par Madame du Châtelet (1706 – 1749) et sa promotion par Voltaire et Maupertuis qu'elle commence à être considérée. On cherche à vérifier cette théorie en testant ses implications pour la forme de la Terre, qu'elle prédit aplatie selon l'axe de rotation.
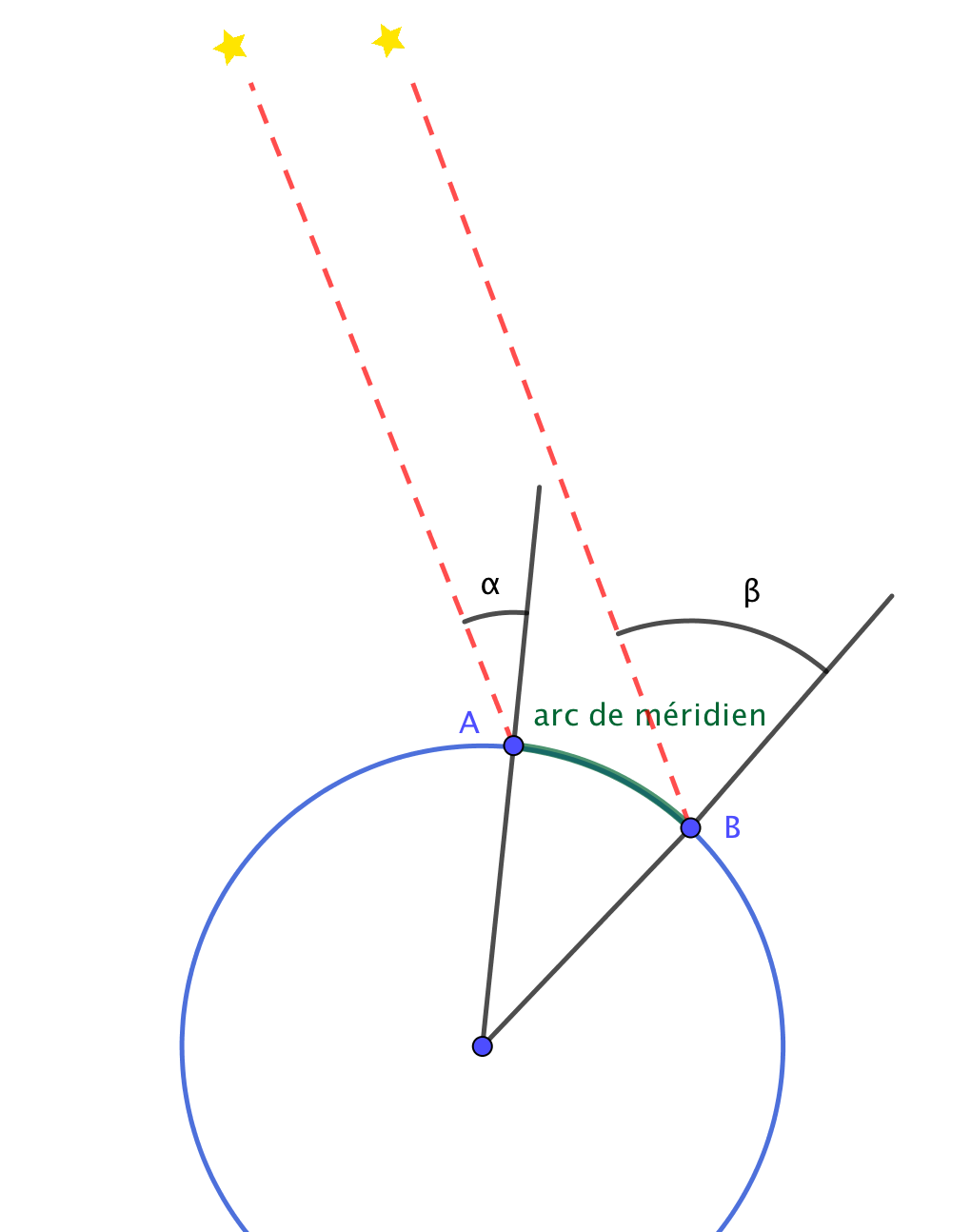
Figure 1. Mesure de distance au XVIIIe siècle, par visée Principe de mesure d'une distance angulaire méridienne par visée d'une étoile lointaine (pour une représentation plus aisée, l'étoile pointée est représentée deux fois alors que c'est le même objet mais très éloigné de la Terre). Mesurer un arc de méridien revient à mesurer la distance parcourue sur le méridien pour faire basculer la verticale du lieu d'une valeur déterminée. Sur une Terre ellipsoïde de révolution, et donc sur un méridien elliptique, la "bascule" de la verticale est plus "rapide" vers le côté allongé et plus "lente" vers la partie aplatie : l'arc de méridien est plus court quand on se rapproche du grand axe, donc de l'équateur si on suit Newton, et des pôles si Cassini a raison. |
En France, cet objectif s'inscrit plus largement dans le travail de cartographie du pays et de mesure des distances. L'abbé Jean-Félix Picard (1620 – 1682) avait ainsi mesuré par triangulation l'arc reliant Paris à Amiens, toutes deux alignées sur le méridien de Paris. Ayant préalablement défini une toise-étalon[1], il avait obtenu en 1671 une valeur de 57 060 toises pour 1° d'arc de méridien (soit 111,096 km).
Ce résultat est cependant remis en question quelques décennies plus tard. Les expéditions de Laponie et du Pérou de Maupertuis et la Condamine viennent confirmer la théorie newtonienne dès 1737.
La polémique sur la forme de la Terre découlait des mesures effectuées sur le méridien de Paris par Jacques Cassini (Cassini II, 1677 – 1756) à l'aide d'une toise étalon probablement identique à celle de Picard. En 1738, César-François Cassini[2] (1714 – 1784) et Pierre Charles Le Monnier (1715– 1799) sont ainsi chargés de vérifier les mesures de l'abbé Picard. En association avec Maupertuis, revenu de Laponie, Le Monnier obtient une valeur de 57 183 toises (soit 111,335 km) en reprenant les mesures astronomiques tout en conservant comme référence des longueurs la toise de Picard.
En association avec Cassini III, l'abbé Nicolas Louis de La Caille (1713 – 1762) réexamine à son tour cet arc de méridien en 1740, mais en utilisant une nouvelle référence, la toise du Châtelet, étalonnée en 1735. Les mesures qu'il réalise, à l'aide de bâtons de quatre toises, entre Juvisy et Villejuif, pour établir la base de sa triangulation (le premier côté de sa série de triangles) montrent une différence faible mais systématique avec celles de Picard.
Tableau 1. Comparaison des résultats des mesures de Picard et de La Caille dans leur évaluation de la base de Juvisy (en toises)
Picard (1671) | 2512,25 | 1971,79 | 1179,00 | 5663,04 |
La Caille (1740) | 2509,65 | 1969,78 | 1177,86 | 5657,29 |
Ces mesures à presque 70 ans d'écart des mêmes longueurs de référence de la base de Juvisy montrent un écart systématique, les mesures de Picard sont plus longues de l'ordre de 1‰.
Source - © ~1740 La Caille / Observatoire de Paris
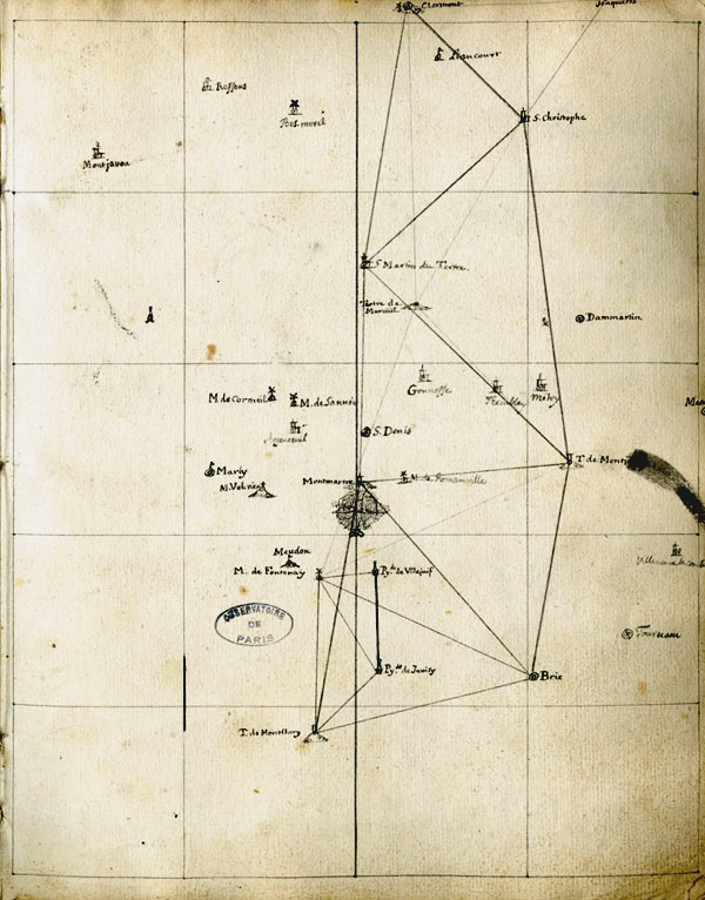
Figure 2. Mesure de distance au XVIIIe siècle, par triangulation
Dessin de La Caille montrant la triangulation effectuée de la Tour de Montlhéry à Clermont de l'Oise et la base réalisée entre Villejuif et Juvisy.
La Caille attribue cet écart à la toise de Picard, ce que soupçonne également Pierre Bouguer (1698 – 1758), pour qui cette toise serait d'un millième plus courte que celle du Châtelet. De plus, pour Charles-Marie de La Condamine (1701 – 1774), chef de l'expédition de mesure du degré de méridien au Pérou, le pendule à secondes utilisé par La Caille aurait lui aussi été ré-étalonné avec la toise du Châtelet par rapport à celui employé par Picard[3].
À Paris, Picard avait mesuré la longueur du pendule battant la seconde à 440,5 lignes (99,37 cm). Mais en 1735, avec les nouvelles toises-étalon, Jean-Jacques Dortous de Mairan (1678 – 1771) la réévalue à 440 lignes et 17 trentièmes de ligne (440,57), soit un écart d'un quinzième (soit seulement 0,15 mm). Par ailleurs, l'abbé Picard écrit que « la longueur de la toise de Paris et celle du pendule seront soigneusement conservées dans le magnifique observatoire que Sa Majesté fait bâtir pour l'avancement de l'astronomie » mais ces étalons n'y ont jamais été retrouvés, si tant est qu'ils y aient effectivement été déposés.
Source - © 1762 Anne-Louise Le Jeuneux / Wikimedia
2. Les mesures de la pesanteur
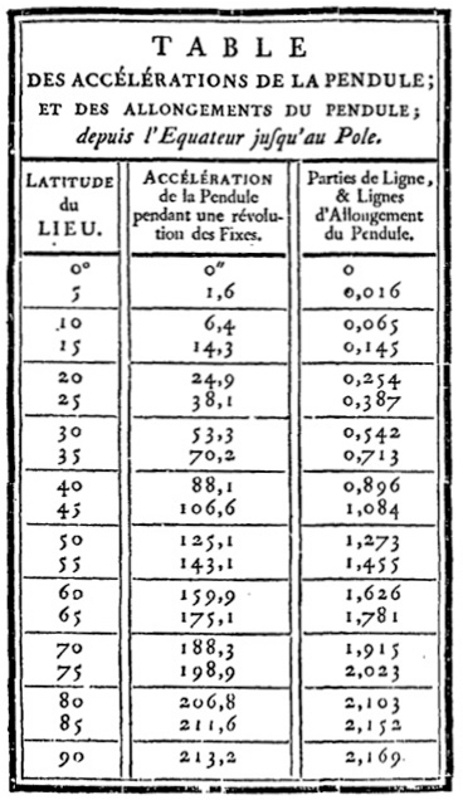
Ainsi, au cours de son expédition en Laponie, Maupertuis observe à Pello (66°48'N) que son horloge à pendule, réglée à Paris, avance sur l'heure parisienne de 59,1 s au bout d'une journée. La pesanteur à Pello est donc supérieure à celle de Paris de 0,001369. Maupertuis en déduit la longueur du pendule à seconde à Pello, soit 440,57 × 1,001369 = 441,17 lignes. Il publie également, en 1738, dans La figure de la Terre déterminée par les observations, une table des valeurs relatives de g (par rapport à la pesanteur à Paris) à différentes latitudes (à Pello, à Paris, à Cayenne, etc.), valeurs calculées par proportionnalité sur la base de ses résultats à Pello.
Source - © 1738 Maupertuis et al., in La figure de la Terre..., p.181
Sur le même sujet, on pourra consulter l'article « La découverte historique de la variation de la pesanteur avec la latitude » de Vincent Deparis.
3. Les alternatives à la gravité newtonienne
Une trentaine d'années plus tard se développe en France une controverse entre les partisans de la physique de Newton, axée sur les mathématiques, et des physiciens plus tournés vers l'observation. L'étrangeté de la théorie newtonienne tient à ce qu'elle se dispense de chercher une matérialité physique à la force d'attraction gravitationnelle, comme l'écrit Newton lui-même :
« Mais je n'ai pas encore pu découvrir à partir des phénomènes la raison de ces propriétés de la gravitation et je n'imagine pas d'hypothèse. Eh bien, ce qu'on ne déduit pas des phénomènes doit être appelé hypothèse, et les hypothèses, métaphysiques, physiques de qualités occultes ou mécaniques, n'ont pas leur place dans la philosophie expérimentale [...] Et il suffit que la gravité existe de fait et agisse selon les lois exposées par tous les mouvements des corps célestes et de notre mer. »
Ces physiciens publient ainsi, dans des journaux "alternatifs", des résultats contradictoires avec la théorie de la gravitation de Newton, notamment une augmentation de la pesanteur avec l'altitude. On en trouve indirectement la trace dans les écrits de D'Alembert, qui étudie l'effet gravitationnel des montagnes pour tenter d'expliquer ces résultats. En réalité, il semble que ces expériences et ces physiciens expérimentateurs n'aient jamais existé ! L'identité de l'auteur (ou des auteurs) de cette mystification reste inconnue, même si certains l'attribuent à Joseph Étienne Berthier (1702 – 1783).
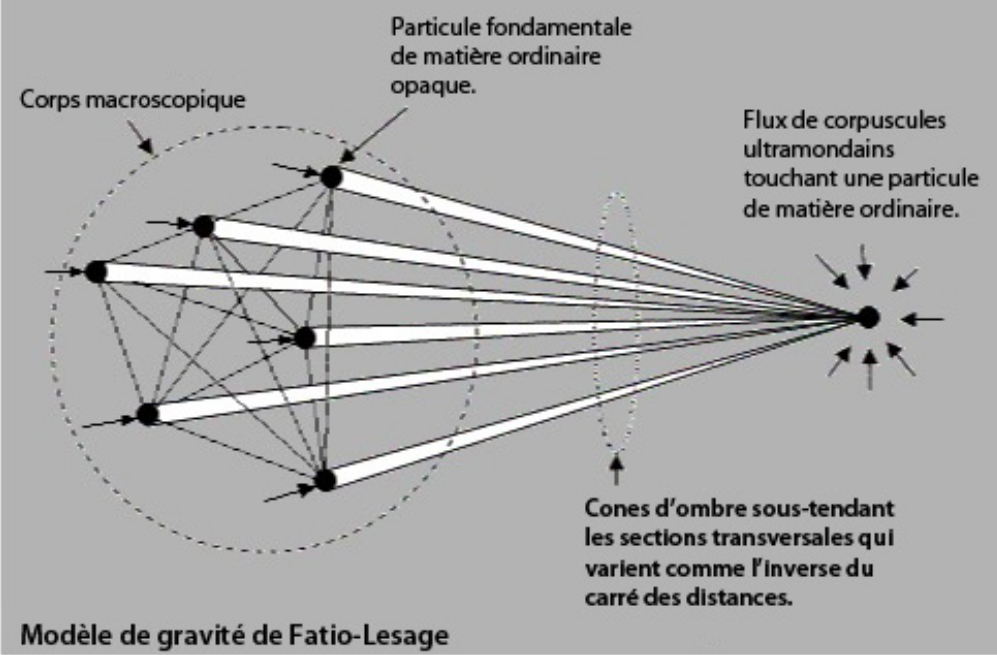
Cette supercherie fut dévoilée par le physicien suisse Georges-Louis Lesage (1724 – 1803), qui tenta, lui, d'avancer une explication matérialiste à la gravitation. Lesage propose d'expliquer les propriétés de la gravitation par l'action de particules matérielles, qu'il nomme « corpuscules gravifiques ultramondains ». La loi du carré inverse s'expliquerait alors par un raisonnement géométrique : les corpuscules qui traversent un corps se concentrent, en le pénétrant, dans des sphères de plus en plus petites ; la surface de ces sphères étant proportionnelle au carré de leur rayon, l'effet des corpuscules ainsi concentrés augmenterait en proportion (figure 6) :
« Si donc, une Particule de Matière (beaucoup trop petite pour que nos sens puissent la distinguer, mais beaucoup plus grande cependant qu'un Corpuscule Ultramondain) ; occupe [un] point de l'Espace ; & arrête par conséquent, tous les Corpuscules qui s'étoient avancés vers ce Point, de sorte qu'il n'y en ait plus qui en reviennent : On pourra concevoir ceux qui y vont comme traversant successivement diverses surfaces sphériques, concentriques à cette Particule. Et comme les Corpuscules qui traversent une de ces surfaces, sont exactement les mêmes que ceux qui ont traversé tout autre d'entr'elles, plus éloignés ; ils y seront d'autant plus serrés, que celle-là sera moins étendue que celle-ci. Or, les surfaces des Sphères, sont quadruples de celles de leurs grands Cercles respectifs : Et celles-ci sont entr'elles comme les quarrés de leur diamètre ; & par conséquent, de leurs demi-diamètres ; qui sont ici, les Distances de ces surfaces à la Particule. »
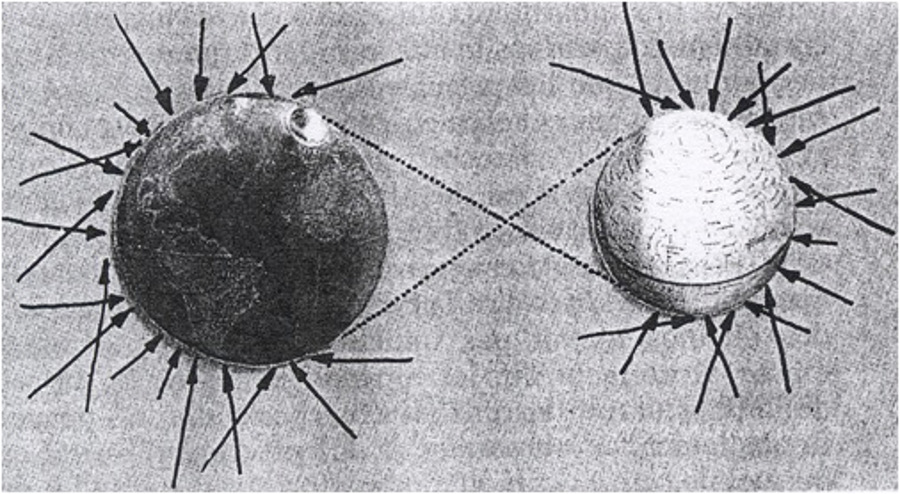
Quant à l'attraction entre deux corps, elle s'expliquerait, pour Lesage, par une différence de fréquence des interactions corps - corpuscules en dehors et à l'intérieur de l'espace séparant les deux objets, qui seraient ainsi « poussés » l'un vers l'autre (figure 5). Cette théorie, si elle échoua à expliquer la gravité, inspira cependant William Thomson (lord Kelvin, 1824 – 1907) pour élaborer sa théorie cinétique des gaz.
Source - © --- In J.-M. Lévy-Leblond Aux contraires, L’exercice de la pensée et la pratique de la science, Gallimard, 1996, ISBN:9782070745340
Lesage alla plus loin en tentant d'expliquer la proportionnalité de la force d'attraction gravitationnelle avec la masse des objets et non avec leur surface. Cette observation semblait invalider toute les explications de la gravité par l'effet d'un « fluide gravifique », comme le proposait Descartes dans son modèle des « tourbillons ». Lesage postule donc que les corps pesants doivent être fondamentalement poreux, leur interaction avec les corpuscules ultramondains devenant ainsi proportionnelle à leur volume et donc à leur masse (figure 7) :
« Des Corpuscules Isolés, très subtils, qui se meuvent en ligne droite, dans un grand nombre de sens différens, & qui rencontrent des Corps fort Poreux. Voilà donc la seule façon dont peut exister la Cause matérielle des Attractions ». (Lesage, 1761)
Source - © .... Traduit d'après K. Brown sur MathPages Figure 6. Les corpuscules ultramondains, éléments de la théorie de l'attraction gravitationnelle de Lesage Schéma conceptuel de la loi du carré inverse de l'attraction gravitationnelle selon les conceptions de Lesage. | Source - © 1758 G.-L. Lesage, in Essai de chymie méchanique, p.44 Figure 7. Les corps « très poreux », éléments de la théorie de l'attraction gravitationnelle de Lesage Les corps « très poreux » sont envisagés par Lesage pour expliquer la proportionnalité de la gravité avec la masse plutôt que la surface des corps. |
4. Pistes d'exploitation
5. Les autres articles du dossier La Terre, sa forme, sa taille, sa rotation :
- La Terre est ronde ! Ératosthène et la mesure du rayon terrestre
- Les mesures de méridien vont-elles confirmer la théorie de Newton ?
- Clairaut et sa bande, l'expédition de Clairaut et Maupertuis en Laponie
- La Terre tourne... Le gyroscope de Foucault
- Les machines de lord Kelvin
- Les marées depuis Newton
[1] 1 toise Picard = 1,947 m.
[2] César-François Cassini dit Cassini de Thury ou Cassini III, fils de Jacques Cassini.
[3] Rappelons que la période des oscillations T d'un pendule est liée à sa longueur l et à la pesanteur g par T = 2π ·√ (l/g). La longueur d'un pendule de période T fixée (de demi-période 1s au XVIIIe siècle) est donc proportionnelle à g.
Pour citer cet article :
La Terre ellipsoïde ? Les mesures de la gravité au XVIIIe siècle, juin 2018. CultureSciences Physique - ISSN 2554-876X, https://culturesciencesphysique.ens-lyon.fr/ressource/Terre-ellipsoide-gravite.xml