La Terre est ronde ! Ératosthène et la mesure du rayon terrestre

Les images spatiales disponibles depuis les années 1960 nous ont rendu familière la forme de la Terre. Pour comprendre comment l'homme a pu deviner sa forme par le passé, on commencera par remonter à la période de l'Antiquité qu'au milieu du XIX^e siècle l'historien Ernest Renan a qualifiée de « miracle grec ».

Source - © 20-07-1969 D'après NASA - Apollo 11, modifié

La Terre vue de la Lune par la mission Apollo 11

À partir du V^e siècle avant J.-C. environ, sur le pourtour de la mer Égée, dans les villes de la Grèce continentale, des îles du Dodécanèse et d'Ionie (sur la côte occidentale de la Turquie), puis plus tard à Alexandrie, l'explication des phénomènes naturels cesse de faire appel à l'intervention directe de divinités, et la « philosophie de la nature » commence à se constituer en science.

Ce « miracle » est en réalité tributaire d'une histoire antérieure entamée en Mésopotamie et en Égypte, mais qui reste trop peu connue : la majorité des sources disponibles nous viennent de l'Antiquité grecque. Depuis Alexandrie, cette tradition scientifique a été reprise et complétée par les Arabes, dans les grands centres culturels comme Bagdad, Damas, Le Caire puis Cordoue, d'où elle se propagea vers l'Occident à la faveur des contacts entre Arabes et Occidentaux aux XII^e et XIII^e siècles.

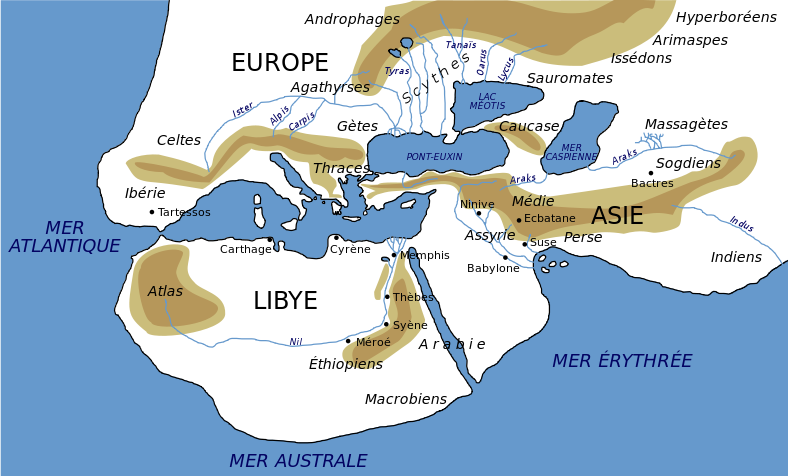
Source :Herodotus_world_map. Figure 1. Reconstruction du monde décrit par Hérodote dans son Enquête (Ve siècle av. J.-C.)

Source - © 2018 Jean-Benoît Bouron, ENS de Lyon/DGESCO Figure 2. Carte du bassin Méditerranéen et du monde arabo-musulman (VIIIe siècle ap. J.-C.)

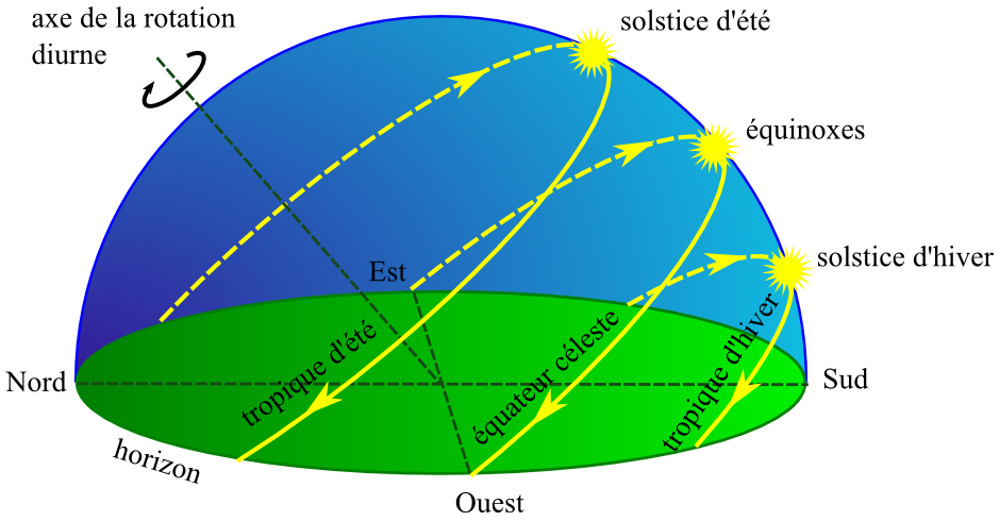
La Grèce hérite des connaissances astronomiques des Babyloniens, parmi lesquelles la connaissance des équinoxes et des solstices, figure 3, ainsi que de l'obliquité de l'écliptique : le Soleil au zénith indique la direction de midi, donc méridienne, Nord-Sud ; par contre, le Soleil n'indique précisément l'Est et l'Ouest que deux fois par an, à son lever et à son coucher aux équinoxes.

De plus, dès 600 avant J.-C., les observations des marins phéniciens naviguant autour des côtes africaines appuient également l'idée d'une courbure de la Terre (les marins observent les sommets des montagnes avant les côtes, ou la lumière du phare d'Alexandrie avant les lumières de la ville). Elle est aussi envisagée à partir des observations astronomiques : la rotation des astres autour d'un « pôle céleste » (rotation de la Terre) et la variation d'inclinaison de ce pôle en fonction du lieu (détermination de la latitude), ou encore l'interprétation des éclipses de Lune (l'ombre de la Terre sur la Lune est toujours arrondie), par exemple.

Source - © 2017 Vincent Deparis Figure 3. Le trajet du Soleil sur la voûte céleste (hémisphère Nord) La structure du Monde (1/3) - Du cosmos des mythologies au géocentrisme

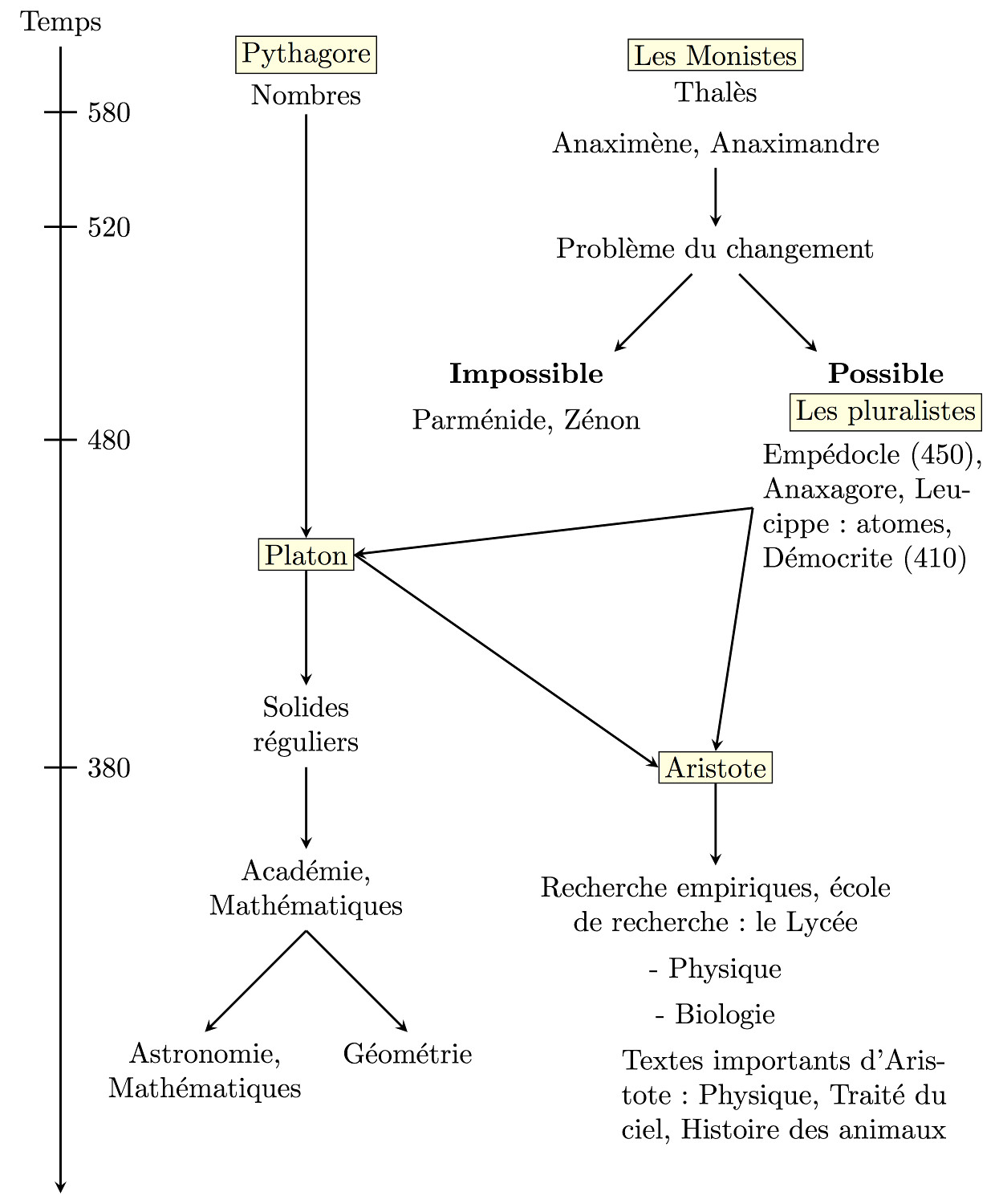
La science grecque se développe d'abord sur les côtes ioniennes. Le premier nom qui nous soit parvenu est celui de Thalès (625 – 547 av. J.-C.), habitant de la riche cité marchande de Milet. Lui-même commerçant autant qu'ingénieur et politicien, Thalès applique ses connaissances mathématiques à des problèmes techniques de navigation et de génie civil. Il conçoit la Terre comme un disque ou un cylindre flottant. L'un de ses élèves supposés, Anaximandre, dresse les premières cartes du ciel et introduit dans l'astronomie grecque l'usage du gnomon, (section 3) probablement d'origine babylonienne.

Pour les héritiers de la pensée de Thalès, une question centrale est celle du changement, désigné alors par le terme de « mouvement », qui a, à l'époque, un sens beaucoup plus large que celui de la physique moderne : pourrissement, vieillissement, transformation ou déplacement sont tous "mouvement".

Parallèlement à l'école ionienne de Thalès s'épanouit, depuis Crotone en Calabre, celle de Pythagore, fondée sur les nombres et la géométrie, figure 4. L'école pythagoricienne affirme par principe la sphéricité de la Terre : la sphère représentant la plus parfaite des formes géométriques, la Terre ne peut avoir d'autre forme que sphérique. C'est à cet héritage que l'on peut faire remonter l'omniprésence de la sphère dans toute l'imagerie astronomique.

Source - © 2016 Cyril Langlois Figure 4. Repères chronologiques et intellectuels dans la pensée antique

C'est dans la continuité de ces connaissances qu'Aristote (384 – 322 av. J.-C.) soutient lui aussi que la Terre est ronde. À la différence de Platon, dont il a fréquenté l'Académie à Athènes vers 367 av. J.-C., Aristote refuse de ne décrire la nature qu'en termes mathématiques, sans recherche empirique. On trouve ainsi dans son Traité du ciel (II, 14) : « D'après la manière dont les astres se montrent à nous, il est prouvé que non seulement la Terre est ronde, mais même qu'elle n'est pas très grande, car il nous suffit de faire un léger déplacement, vers le Sud ou vers l'Ourse, pour que le cercle de l'horizon devienne évidemment tout autre ».

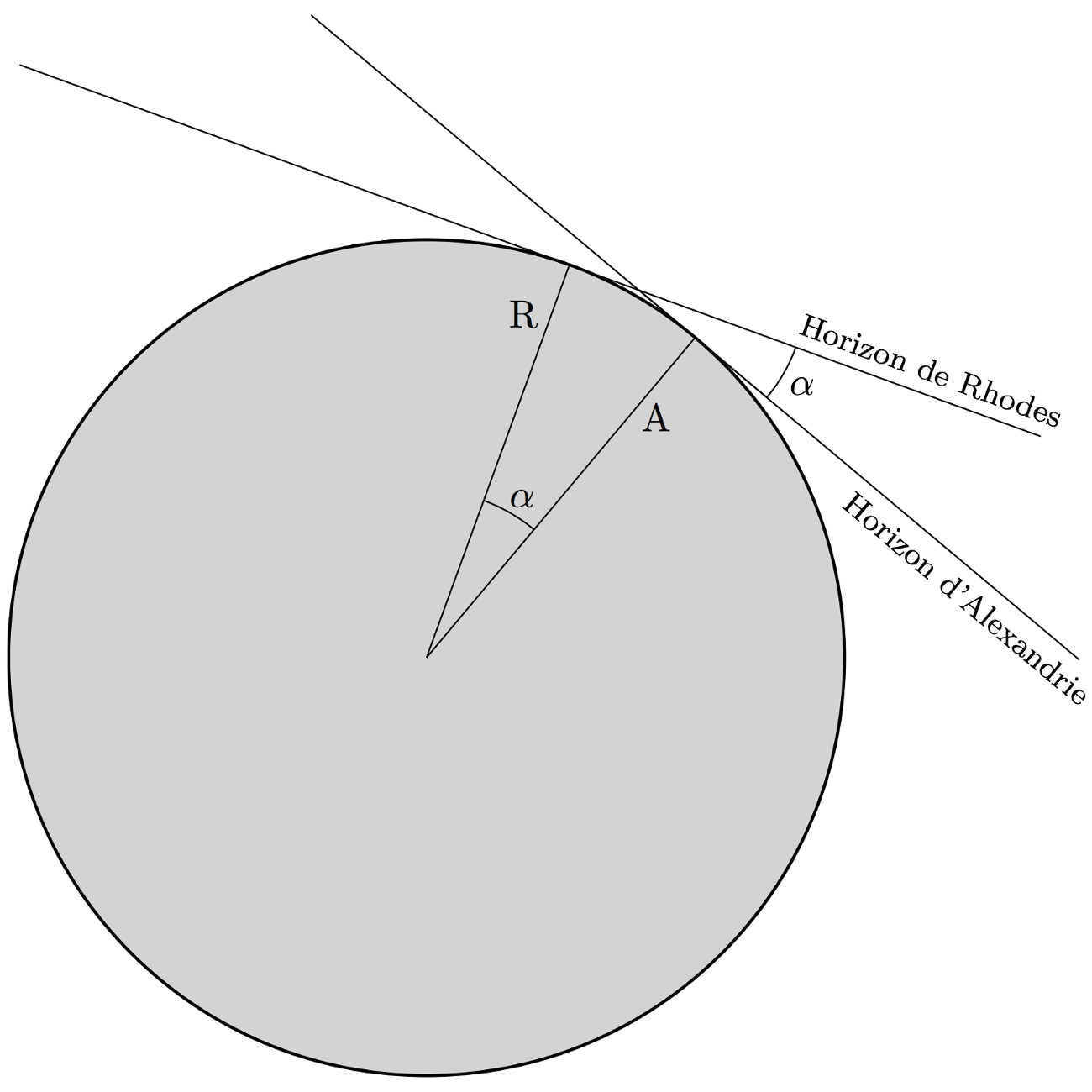
L'estimation de la taille de la Terre est effectivement tentée par les grecs en observant l'heure de lever des étoiles dans deux lieux supposés sur le même méridien, Rhodes (36°10'00''N, 28°0'0''E) et Alexandrie (31°11'53''N, 29°55'9''E), figure 5. L'étoile Canopus se prête particulièrement bien à ce calcul. Lorsqu'elle culmine à 0° à Rhodes (brève apparition et disparition sur le même point de l'horizon), elle culmine alors à 7,5° à Alexandrie à cette même date. Les deux cités sont donc séparées par 1/48^e (7,5/360) de circonférence terrestre. Ce calcul basé sur l'observation de Canopus est attribué au stoïcien Posidonius d'Apamée (135 – 51 av. J.-C.) par un autre philosophe stoïcien, Cléomède.

Source - © 2016 Cyril Langlois Figure 5. Principe de la mesure de la circonférence de la Terre par Posidonius

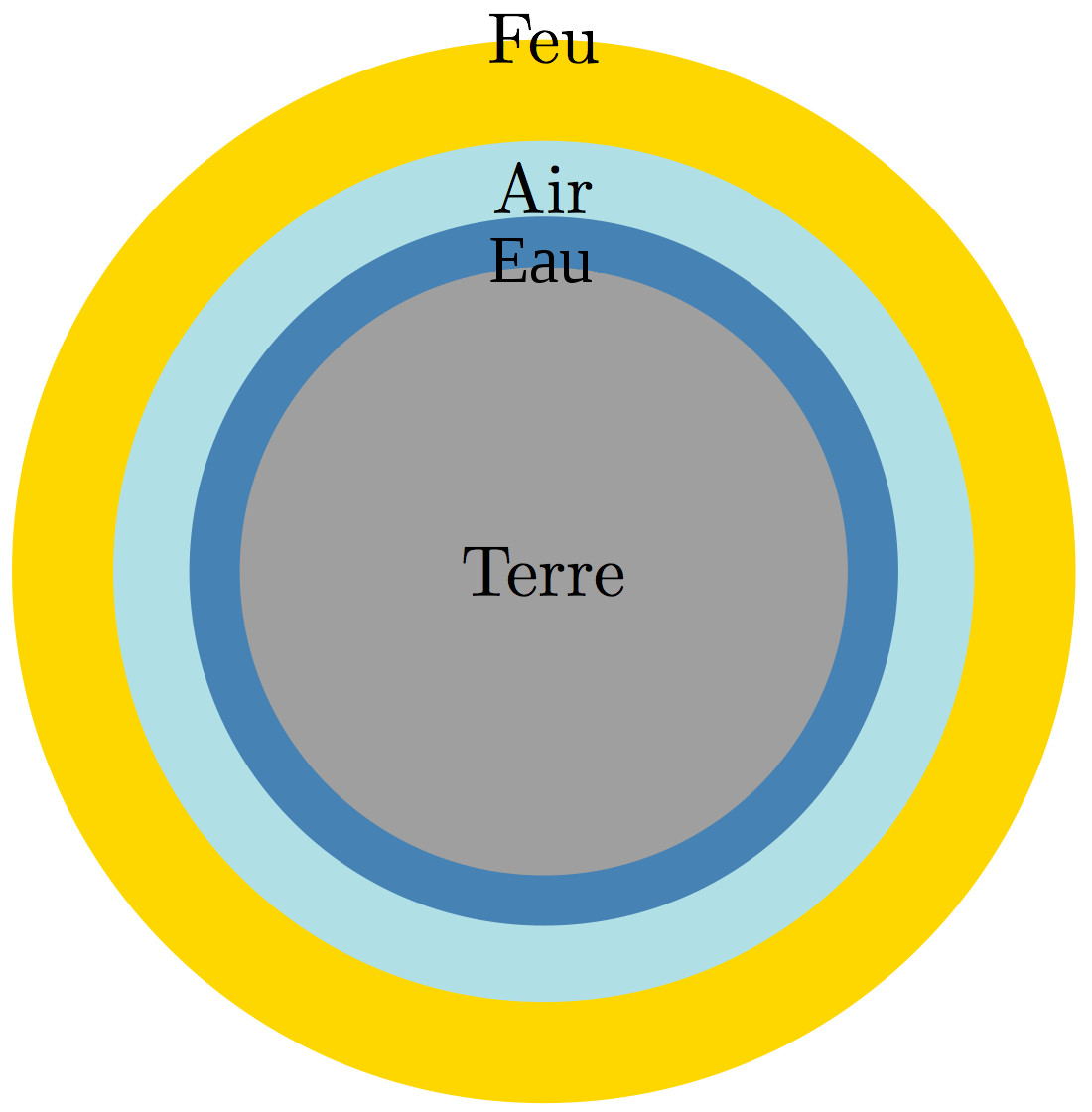
Par ailleurs, la science antique se divise nettement en deux branches : la physique, qui étudie la Terre, et l'astronomie, elle-même dérivée des mathématiques et consacrée au ciel. Selon Aristote et son école, le Lycée d'Athènes^[1] (dont les idées seront reprises au Moyen-Âge car plus compatibles avec la doctrine chrétienne), cette dichotomie entre le ciel, monde idéal situé au-delà de l'orbite de la Lune, et le « monde sublunaire », s'ajoute à une anisotropie fondamentale du domaine terrestre. Ce dernier se hiérarchise en quatre régions emboitées : terre, eau, air et feu, figure 6.

Le comportement de tous les objets matériels s'interprète par leur affinité avec l'un ou l'autre de ces domaines : la chute des corps solides s'explique par leur appétence pour la terre, située au centre ; la montée des flammes par leur « tendance » spontanée à rejoindre le domaine igné, le plus externe. Dans le monde terrestre aristotélicien, tout objet est donc nécessairement en « mouvement », qu'il se déplace dans l'espace ou qu'il évolue dans le temps et tout changement a un objectif, une fin : l'étude du mouvement est nécessairement téléologique (du grec "teleo" : fin, but). Au contraire, le ciel parfait est immuable ; par conséquent, il ne peut montrer d'autres changements que cycliques et ne peut pas être formé de la même matière que le monde terrestre : les cieux sont constitués d'un milieu spécifique, l'éther.

Source - © 2016 Cyril Langlois Figure 6. L'organisation anisotrope du monde d'Aristote

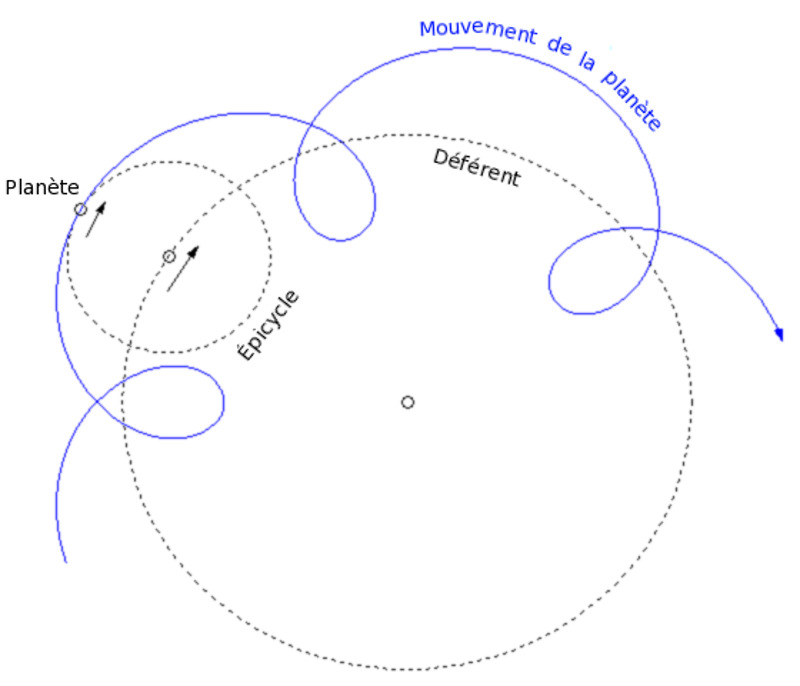
Le travail des astronomes est donc d'expliquer, par des mouvements cycliques, le comportement hétérodoxe de certains astres, les planètes (πλανήτης ἀστήρ, "astre errant" en grec) : Mercure, Vénus, le Soleil, Mars, Jupiter, Saturne et la Lune. Apollonius de Perga (v. 240 – 190 av. J.-C.) puis Ptolémée (v. 100 – 170 ap. J.-C.) y parviendront en combinant deux mouvements circulaires pour chaque planète, déférent et épicycle (figure 7), « sauvant ainsi les apparences », selon l'expression de Ptolémée lui-même.

Source - © 2005 Dhenry - CC BY 1.0 Figure 7. Déplacement schématique d'une planète selon la théorie des épicycles d'Apollonius

Au contraire des phénomènes célestes, les mouvements du monde terrestre sont rectilignes, finis et imposés par une « cause finale », liée à leur nature. Leur étude ne passe pas par les mathématiques, mais par la seule observation. Par ailleurs, le mouvement naturel des objets, régi par le système d'Aristote, est également distingué du mouvement créé par l'Homme, considéré comme « forcé », « contre nature ». La physique grecque se divise ainsi entre la connaissance fondée sur l'observation des phénomènes naturels, l'épistèmê, et l'obtention des règles pour agir sur les objets, la technê.

Au cours de l'histoire, le foyer principal de la science grecque se déplace de la mer Égée au delta du Nil. À l'époque hellénistique^[2]. Sous l'impulsion de la dynastie des Ptolémée, qui gouverne l'Égypte au début du III^e siècle avant J.-C., la ville d'Alexandrie, fondée en -331 par Alexandre, devient le principal centre scientifique de la Méditerranée. Sa bibliothèque, le Musée, recueille – ou copie – les textes majeurs du monde antique : les bateaux accostant dans le port de la ville et transportant des livres dignes d'intérêt sont sommés de les confier aux scribes d'Alexandrie qui les recopient et en déposent un exemplaire au Musée. Celui-ci attire ainsi les savants. Euclide et Archimède y auraient travaillé, bien que l'on ne sache pas précisément qui des penseurs grecs dont le nom nous est resté l'ont réellement fréquenté.

L'importance des travaux d'Archimède (287 – 212 av. J.-C.) tient à ce que, en raisonnant en ingénieur pour développer des mathématiques appliquées à des problèmes pratiques, il a pu s'affranchir de la distinction épistèmê / technê et de l'interdiction tacite d'user des mathématiques pour expliquer les phénomènes naturels. Archimède est notamment l'un des savants qui proposent une valeur à la circonférence de la Terre, qu'il estime à 300 000 stades (soit 47 250 km en se basant sur le stade égyptien de 157,5 m). Ses manuscrits seront édités par Ératosthène (v. 276 – v. 194 av. J.-C.), figure 8, précepteur du roi Ptolémée IV et conservateur de la bibliothèque d'Alexandrie à l'âge de 40 ans.

Source - © - Repris de philipkay, modifié Figure 8. Buste d'Ératosthène

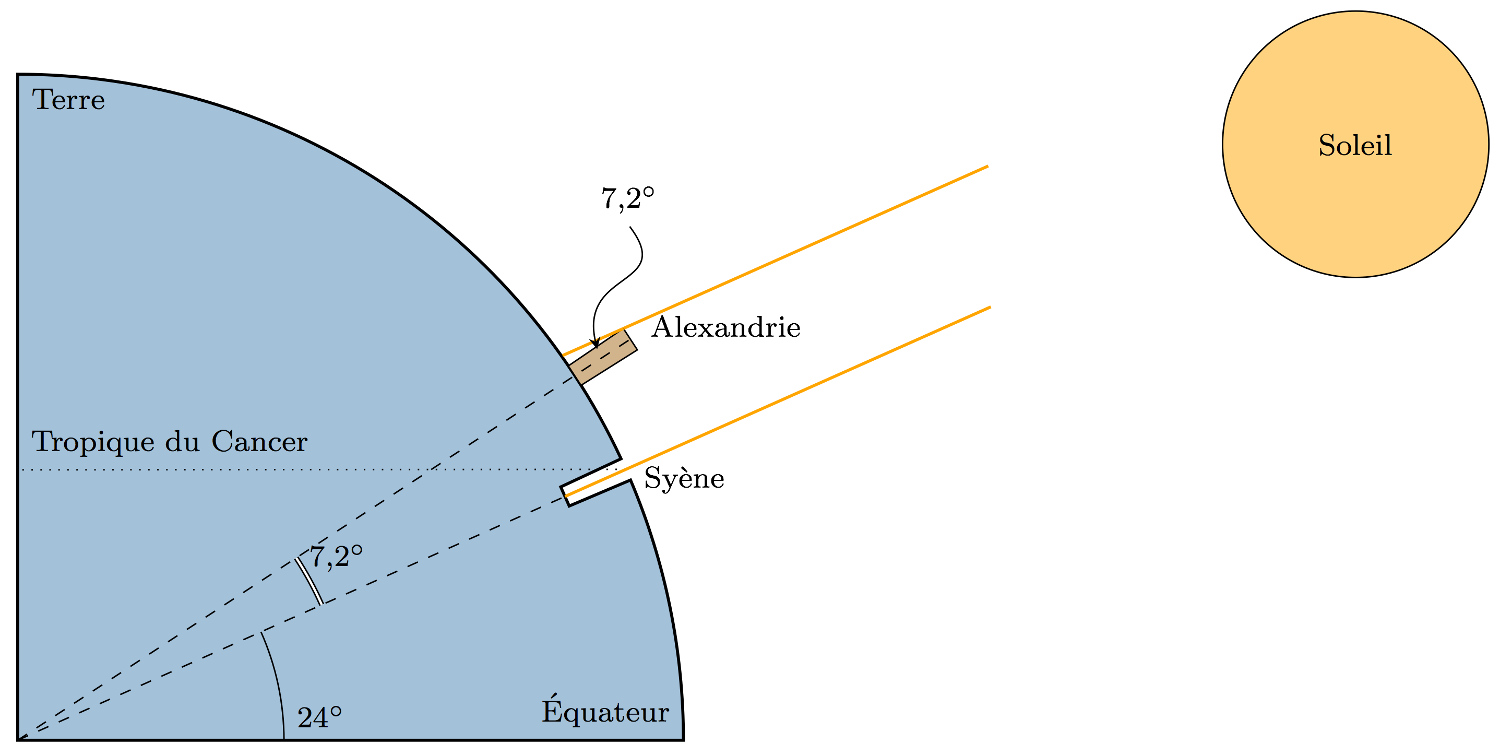
Bien que l'on ne connaisse que quelques fragments de l'œuvre scientifique d'Ératosthène, il serait l'initiateur de la division du globe par un système de lignes méridiennes et latitudinales^[3]. C'est surtout à lui que l'on attribue, à la suite de Cléomède, le calcul d'une valeur correcte de la circonférence terrestre, par le raisonnement et la mesure résumés sur la figure 9.

Ce raisonnement est le suivant :

Source - © 2016 Cyril Langlois Figure 9. Calcul de la circonférence terrestre par Ératosthène Au solstice d'été à Syène (actuelle Assouan, Égypte), à midi, le Soleil éclaire le fond d'un puits. À Alexandrie (côte égyptienne), un obélisque projette une ombre. Ératosthène en déduit l'angle du Soleil avec la verticale du lieu, angle sous lequel on voit l'arc Syène-Alexandrie depuis le centre de la Terre. Avec la distance Alexandrie-Syène, il calcule la circonférence et le rayon terrestre.

Les incertitudes sur le résultat proviennent surtout de la distance estimée pour l'arc Syène-Alexandrie, plus que de celle de l'angle, de 7°12'0'' selon Cléomède. Ératosthène évalue cette distance à 5000 stades, mais la longueur du stade qu'il utilise reste discutée. S'il emploie le stade égyptien, estimé à un peu moins de 160 m (157,5 m), la valeur obtenue pour la circonférence terrestre est proche des 40 000 km admis aujourd'hui. Par ailleurs, le Soleil apparait au zénith à Syène sur un rayon d'environ 50 km, soit 300 stades, d'où une incertitude supplémentaire de 6%.

Soulignons, pour conclure, que ces premières estimations des dimensions terrestres reposaient sur l'utilisation d'un instrument particulier, le gnomon (voir figures 10 et 11). Son invention est généralement attribuée à Aristarque de Samos (310 – 230 av. J.-C.), mais, là encore, un instrument similaire était déjà employé par les Babyloniens, sous la forme d'une bille suspendue, dont l'ombre reproduisait le mouvement du Soleil sur la sphère céleste.

Source - © 2015 Jean-Paul Cornec (réalisation et photographie) Figure 10. Reproduction d'un gnomon à bille ou gnomon babylonien

Source - © 2010 Hartmann Linge sur wikimedia, CC BY-SA 3.0 Figure 11. Exemples de gnomon classique, à bâton Pièce exposée au Clemens Sels Museum de Neuss (Rhénanie du Nord - Westphalie, Allemagne)