Les machines de lord Kelvin

Le physicien William Thomson, devenu baron (lord) Kelvin en 1892, s'intéressa à de nombreux domaines de la physique, notamment la thermodynamique (degré Kelvin, effet Joule-Thomson...). Il occupa une position éminente dans la science britannique (notamment comme président de la Royal Society de 1885 à 1890), corédigea un traité de physique mathématique de référence (Treatise on Natural Philosophy, 1867), et compta également parmi les opposants les plus sérieux à la théorie darwinienne, avançant des arguments physiques à l'encontre des idées de Darwin et du géologue Charles Lyell^[1].

Cette situation en vue et l'abondance de ses publications l'amenèrent à quelques affirmations abondamment citées depuis par ses critiques, comme : “In science there is only physics; all the rest is stamp collecting”^[2][3].

Thomson eut une approche de la physique nettement orientée vers la pratique et l'expérimentation (“I can never satisfy myself until I can make a mechanical model of a thing”^[4] -1884), ce qui le conduisit à divers travaux d'ingénieur. Il participa notamment à la pose d'un câble sous-marin transatlantique en 1865–1866 et, ce qui nous intéresse ici, conçut plusieurs instruments dédiés à l'étude des marées. Ces appareils venaient répondre aux trois problèmes posés à l'ingénieur par les marées : comment les mesurer, comment les analyser et comment les prévoir ?

Source - © ~1885 wikimedia

Figure 1. Lord Kelvin (1824-1907) vers 1885

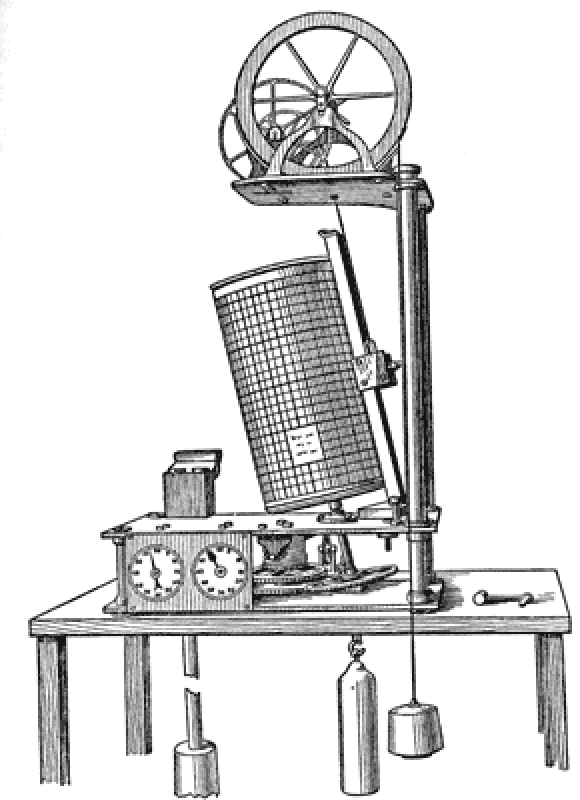
La mesure des marées s'effectuait à l'époque de Thomson à l'aide d'un marégraphe (en anglais, tide gauge). Thomson en conçoit un, représenté ci-dessous sur la figure 2, qu'il décrit, avec ses deux autres appareils, dans un article et une conférence de 1882 ; les variations de hauteur de l'eau, transmises par un flotteur de cuivre suspendu à une roue de platine, sont enregistrées par un stylet sur un tambour incliné, tournant régulièrement sur lui-même en 24 heures.

Source - © 1882 , Sir W. Thomson (Lord Kelvin), in "Evening Lecture to the British Association at the Southampton Meeting, Friday, August 25th, 1882", source 1, source 2 Figure 2. Schéma du marégraphe élaboré par Thomson
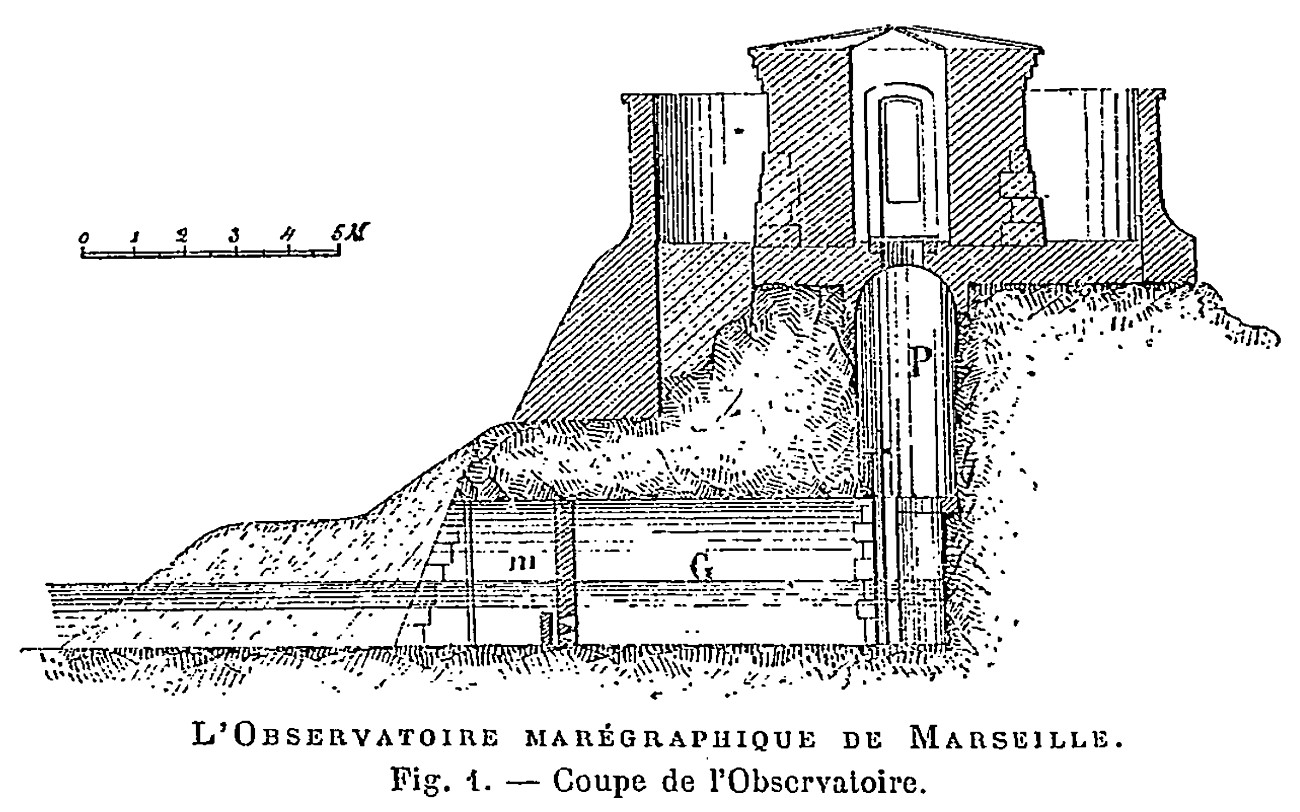
Source - © 2016 AB Associés -Géomètres experts Figure 3. La station marégraphique de Marseille, état actuel	Source - © 1890 L'observatoire marégraphique de Marseille. La science illustrée, VI, 146, 247-250, 13/09/1890 Figure 4. La station marégraphique de Marseille, vue en coupe

En France, c'est l'appareil installé à Marseille (figure 3 et 4) qui définit l'altitude zéro des cartes géographiques et géologiques.

Mais la contribution majeure de Kelvin porta sur deux autres appareils, l'analyseur et le prédicteur de marées, qui reposaient l'un comme l'autre sur le principe de la décomposition de l'onde de marée en une somme de fonctions sinusoïdales.

La marée en un lieu est une somme de fonctions sinusoïdales d'amplitudes et de déphasages distincts, dont les fréquences sont déterminées par les effets des différentes planètes et du Soleil.

Si les fréquences ω_j sont bien connues, les amplitudes (α_j, β_j) et les phases, elles, varient d'un endroit à l'autre et doivent être déterminés à partir de la mesure de la marée u(t). L'appareil conçu par William Thomson, l'analyseur harmonique, décompose mécaniquement l'enregistrement marégraphique en une série d'harmoniques. Thomson décrit cet instrument dans un article de 1878^[5].

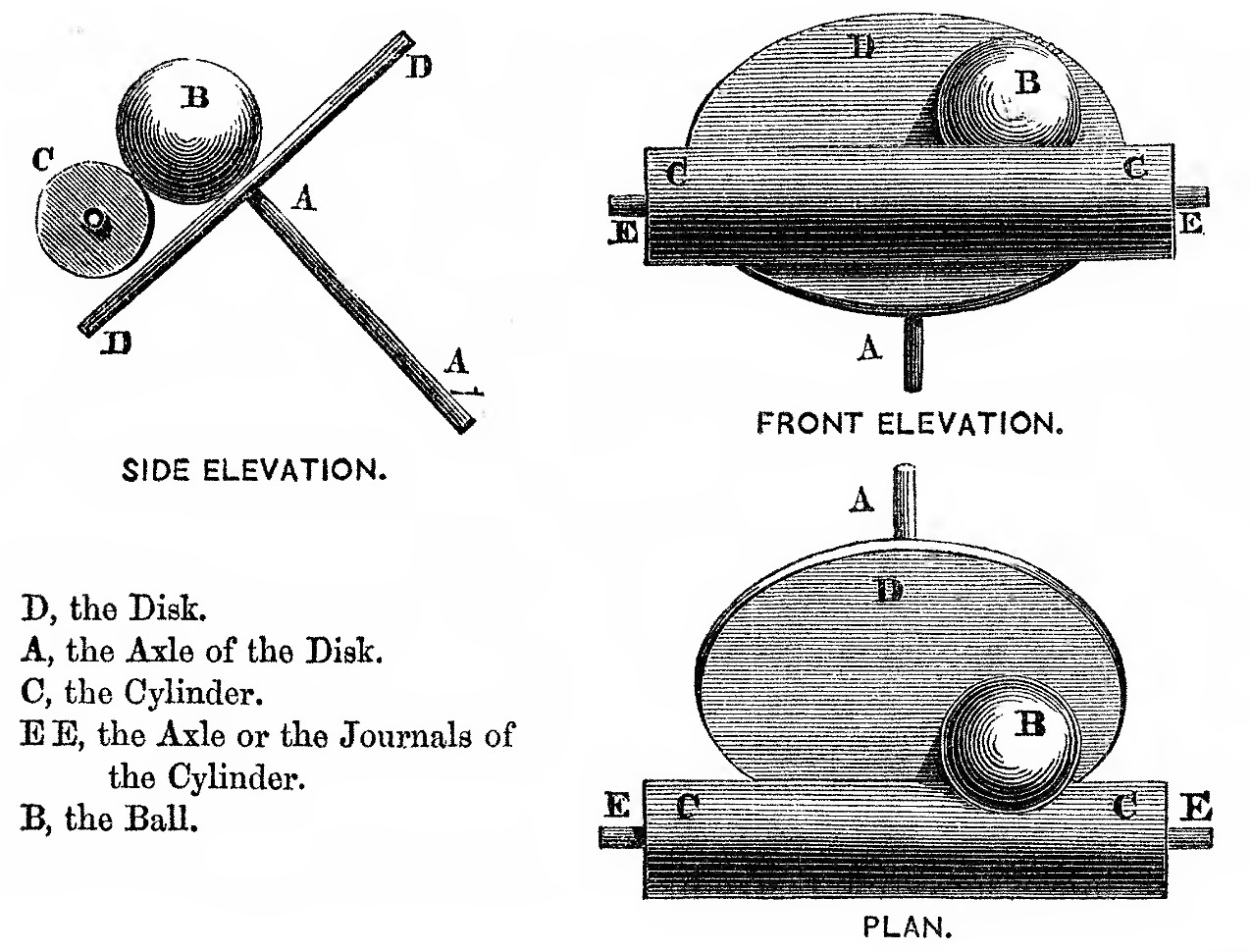
L'appareil utilise un mécanisme conçu par James Thomson, le frère de William, le système disque-sphère-cylindre, par lequel le mouvement de rotation d'un disque vertical ou incliné est transmis à un cylindre horizontal par l'intermédiaire d'une boule roulant sur le disque et en contact avec le cylindre (figure 5) : plus la boule est éloignée du centre du plateau, plus la rotation qu'elle imprime au cylindre horizontal est rapide. Si la rotation du plateau est une fonction g(t) et le déplacement rectiligne de la boule par rapport au centre du disque une fonction f(t), la rotation effectuée sur une durée ∆t par la surface de la boule, et donc par le cylindre, correspond à $\underset{0}{\overset{\mathit{\Delta t}}{\int }}f(t)\cdot g(t)\cdot \mathit{dt}$

Le signal de la marée est enregistré sur un tambour en rotation. Le mouvement vertical de l'eau u(t) est converti en un mouvement horizontal des cardans auxquels sont suspendues les boules : f(t) = u(t). La rotation du tambour sur lequel est enregistré u(t) entraîne quant à lui les disques de l'appareil, chacun avec une vitesse en cos(ω_jt) ou sin(ω_jt)^[6].

Ainsi, pour un disque tournant à la vitesseω_j, la boule effectue, par rapport au disque, le mouvement u(t), et la rotation du cylindre correspond à $\underset{0}{\overset{\mathit{\Delta t}}{\int }}u(t)\cdot \cos ({\omega }_{j}t)\cdot \mathit{dt}$, c'est-à-dire aux coefficients α_j multipliés par ∆t. Chaque cylindre fournit ainsi l'un des coefficients de Fourier du signal.

Source - © 1875 D'après J. Thomson "On an Integrating Machine Having a New Kinematic Principle", Proc. of the royal Society of London, 24, 262-265 (version traduite par M.-J. D.-R. Figure 5. Dessins descriptif du mécanisme de l'analyseur harmonique de Kelvin	Source - © 2008 Andy Dingley sur wikimedia, CC BY 3.0 Figure 6. Détail de deux plateaux de l'analyseur harmonique de Kelvin
Source - © 2008 Andy Dingley sur wikimedia, CC BY 3.0 Une animation de la transmission du mouvement est présentée sur cette vidéo : Friction ball variator (https://www.youtube.com/watch?v=VhTWbcQPMY4). Contrairement à l'analyseur harmonique de Kelvin, le mouvement est ici transmis du cylindre vers le disque. Figure 7. Analyseur harmonique de Kelvin de 1878

Une fois obtenus les coefficients de Fourier de la marée locale, la troisième machine de Thomson, lui, permet de reconstituer le signal, donc de prédire la marée. Le signal de marée est décrit comme une série infinie de cosinus.

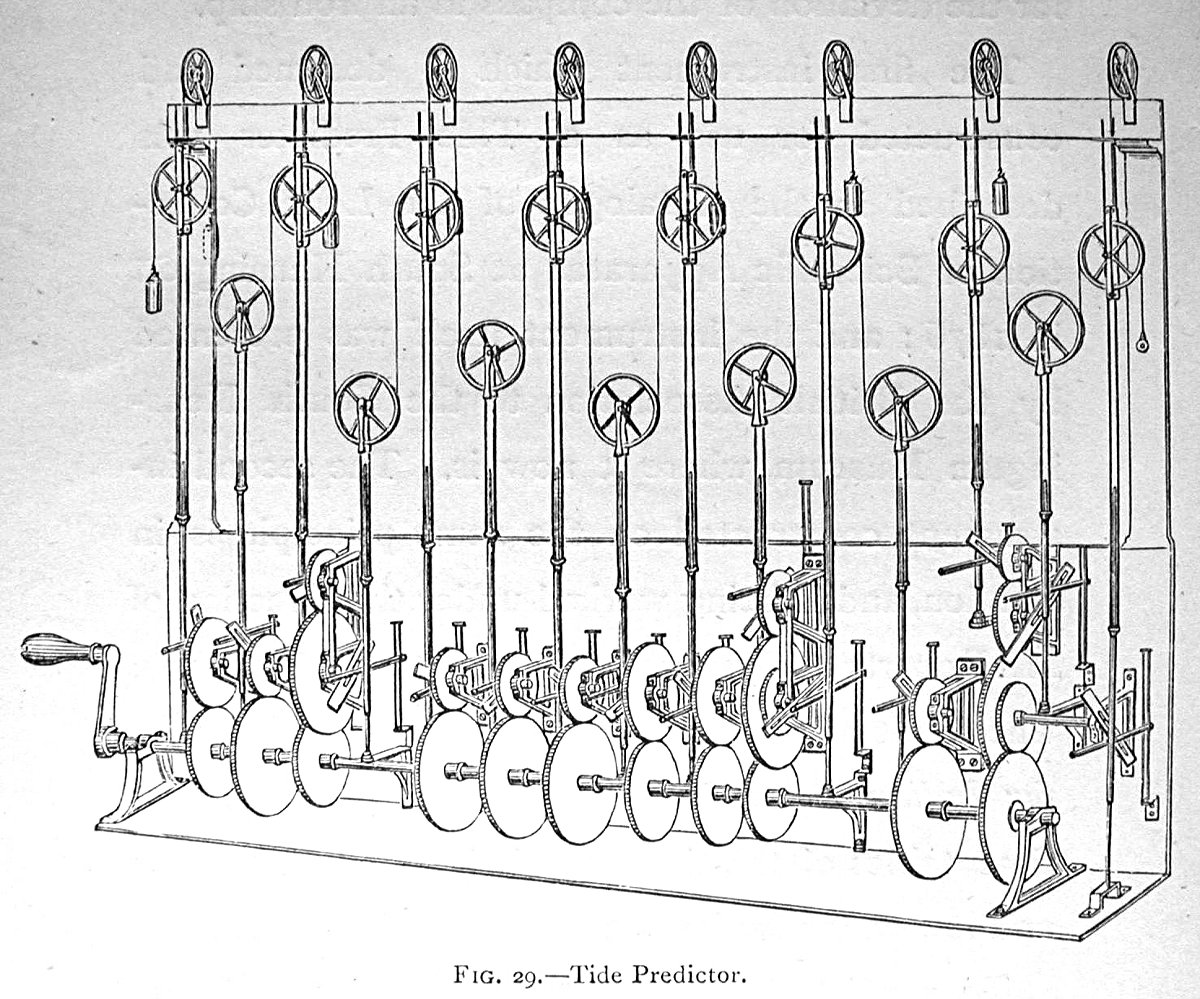
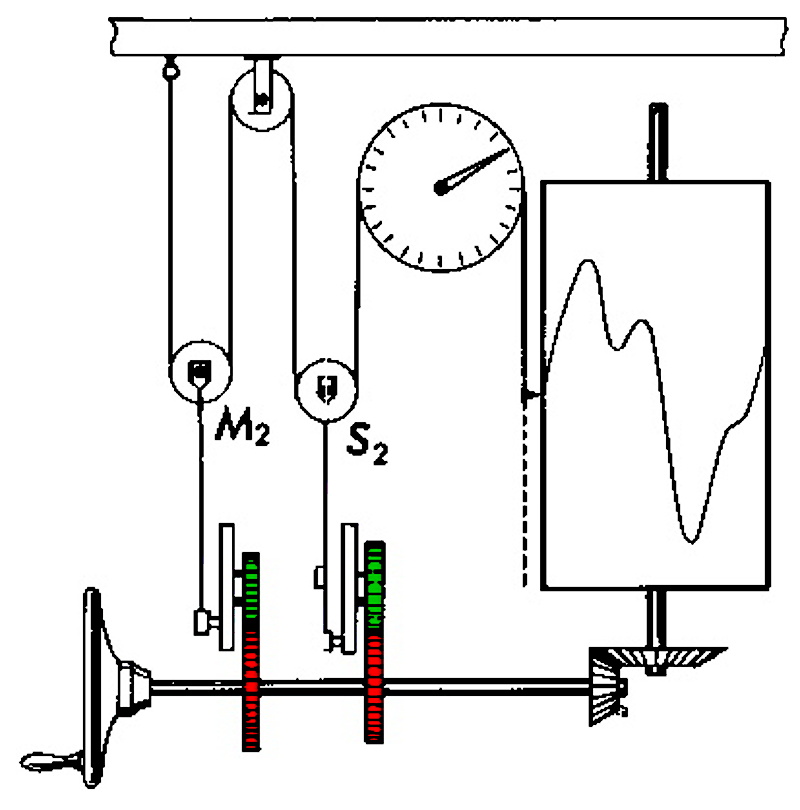
L'appareil de Kelvin, représenté sur les figures 8 et 9, convertit le mouvement rotatif des pignons fixés à la manivelle en un mouvement vertical sinusoïdal, grâce au mécanisme schématisé sur la figure 10. L'éloignement du taquet inséré dans la gouge horizontale par rapport au centre de l'engrenage en rotation spécifie l'amplitude α_j ; la position de ce taquet au démarrage du mécanisme fixe la phase φ_j et la vitesse de rotation de l'engrenage correspond à ω_j. Les mouvements verticaux sont finalement combinés sur l'enregistrement qui s'inscrit sur un tambour lui aussi mis en rotation par la manivelle, dont un tour représente 24 h (figure 11)^[7].

Source - © 1911 d'après "The tidal gauge, tidal harmonic analyser, and tide predicter", in "Kelvin, Mathematical and Physical Papers", source Figure 8. Dessin d'ensemble du prédicteur de marées conçu par Kelvin en 1878-79	Source - © année Science Museum, CC BY-NC-SA 4.0 Figure 9. Prédicteur de marées de Kelvin à 10 composantes Cet exemplaire a été construit en 1876 par A. Légé & Co.
Source - © 1912 E.G. Fischer, in The Coast and Geodetic Survey Tide Predicting Machine No. 2 (Popular Astronomy, 20, 269-285) Figure 10. Mécanisme de conversion du mouvement rotatoire des engrenages en mouvement vertical sinusoïdal	Source - © 1962 Matthias Tomczak, adapté de W.S. von Arx, in "An introduction to physical oceanography" Figure 11. Exemple de tracé par l'appareil de la composition de deux coefficients

Ces systèmes purement mécaniques resteront en usage jusque dans les années 1960, avant d'être définitivement remplacés par les calculateurs numériques puis les ordinateurs. C'est désormais dans les musées consacrés aux instruments scientifiques que l'on peut encore contempler quelques-unes de ces ingénieuses machines (figure 9).