Activer le mode zen
Ressource au format PDF
Classification
La structure du Monde - Du cosmos des mythologies au géocentrisme (1/3)
07/06/2017
Résumé
D'un monde mythologique à un monde intelligible par l'homme.
Table des matières
Articles de la série « La structure du Monde » :
De quoi est fait le Monde ? Comment fonctionne-t-il ? Quelle est son architecture ? Quelle est la place de la Terre ? Jusqu'où s'étend le Ciel ? Dans lemonde occidental, ces questions sont posées "scientifiquement" pour la première fois au tout début du VIe siècle av. J.-C. par des philosophes grecs. Elles inaugurent une toute nouvelle manière d'appréhender le Monde. Dans ce premier article de notre série sur la structure du Monde, nous allons préciser l'audace des savants grecs, qui est double. D'une part, ils dépassent la description mythologique du Monde pour affirmer que la nature est intelligible, qu'elle n'est pas soumise au pouvoir arbitraire des divinités mais qu'elle obéit à des lois qu'il est possible de découvrir. D'autre part, ils intègrent les réflexions astronomiques dans une conception nouvelle de l'espace. Le cosmos qu'ils inventent n'est plus attaché à un contexte social et culturel mais il est perçu d'une manière purement positive et rationnelle. Il devient un espace mathématique, possédant trois dimensions identiques. Il n'est plus réduit à l'écran du Ciel sur lequel se déroule le spectacle du Monde mais il acquiert une certaine profondeur. Nous donnerons ensuite les étapes qui ont permis d'aboutir au géocentrisme, système de pensée qui rend compte de ce qui est perçu dans le Ciel en affirmant que la Terre est immobile au centre du Monde et que tous les astres tournent autour d'elle selon une combinaison de mouvements circulaires uniformes.
La naissance du cosmos grec[1]
Pour les Grecs du VIIIe siècle av. J.-C., vivant au temps d'Homère et d'Hésiode, la Terre est perçue comme un disque à peu près plat, entouré par un fleuve circulaire nommé Océan, sans origine et sans fin parce qu'il se jette en lui-même. Au-dessus de la Terre, comme un bol renversé dont on ne connaît pas bien la forme, s'élève le Ciel inaltérable et indestructible, qui est le domaine des dieux. La Terre est une assise solide et sûre. Sous elle, des racines dont on ne sait pas jusqu'à où elles vont, garantissent sa stabilité. C'est le monde souterrain du désordre, où toutes les directions de l'espace sont mêlées en un chaos inextricable, non encore orienté.
Cet univers mythique possède deux caractéristiques essentielles. Premièrement, c'est un univers à niveaux, hiérarchisé, où les directions ne sont pas équivalentes. L'espace d'en haut est complètement différent de celui du milieu et de celui d'en bas. Le haut est le domaine des dieux, le milieu le domaine des hommes et le bas le domaine de la mort. On ne peut pas passer d'un étage à l'autre. De même, à la surface de la Terre, les directions de l'espace sont différentes : la droite est faste, la gauche est mauvaise ; l'orient, lieu où les astres se lèvent et l'occident, lieu où les astres se couchent, ont des qualités différentes. L'espace n'est pas uniforme, le bas se distingue du haut, la gauche de la droite. C'est un espace associé à une représentation sociale et culturelle. Deuxièmement, l'univers est restreint. Il s'agit de la Terre et de son pourtour immédiat. Le Ciel touche et repose sur le fleuve Océan. Il ne se distingue pas d'une voûte mal définie, semblable aux nuages. Certes, les astres circulent derrière les nuages mais à quelle distance ? Où se situent, par exemple, les comètes et les étoiles filantes ? Les astres ne se distinguent pas clairement des phénomènes météorologiques. Ils restent dans la proximité de la Terre et se déplacent à la surface d'un espace sans réelle profondeur.
Par un effort de pensée prodigieux, les savants grecs vont s'émanciper de cet univers mythique au cours des VIe et Ve siècles av. J.-C. Deux écoles philosophiques y contribuent. D'abord, les philosophes d'Ionie en Asie Mineure, dans la région de l'actuel Izmir. Il s'agit de Thalès (v. 625 – v. 547 av. J.-C.), Anaximandre (v. 610 – v. 546 av. J.-C.), Anaximène (VIe siècle av. J.-C.) et Anaxagore (v. 500 – v. 428 av. J.-C.). Ils sont concernés par les conceptions physiques et par les phénomènes astronomiques et météorologiques. Ensuite, les Pythagoriciens en Italie du Sud, qui était alors grecque. Il s'agit de Pythagore (v. 560 – v. 480 av. J.-C.) et de ses successeurs. Ils sont tournés vers les considérations mathématiques et vers une description géométrique de l'univers. Pour dégager les caractéristiques essentielles du nouveau cosmos inventé par les Grecs, nous allons donner des citations de quelques auteurs et les commenter. Mais il ne faut pas oublier que cette période est très mal connue et que les informations dont nous disposons ne proviennent que de sources secondaires, parfois contradictoires.
Le cosmos devient un cosmos géométrique
Anaximandre est un élève de Thalès. Il vit pendant la première moitié du VIe siècle à Milet en Ionie. D'après Hippolyte [Tannery, réf10, p.119] : « Il [Anaximandre] a dit que la Terre est isolée sans tenir à rien ; elle reste en place à cause de l'égalité de distance de tous les côtés ; sa forme est arrondie circulairement et semblable à celle d'une assise de colonne ; il y a deux faces planes opposées, sur l'une desquelles nous nous trouvons. Les astres sont des cercles de feu dégagés du feu cosmique et enveloppés d'air ; il y a des évents, sortes de trous allongés en tuyau, ce qui donne l'apparence des astres ; aussi quand ces évents se bouchent, il y a éclipse. La fermeture ou l'ouverture de ces trous fait également paraître la Lune tantôt pleine et tantôt échancrée. Le cercle du Soleil est 27 fois (celui de la Terre) et celui de la Lune (18 fois) ; le Soleil est au plus haut, les cercles des étoiles fixes, au plus bas ».
Pour Anaximandre, la Terre a une certaine forme, un dessus, un dessous, une épaisseur. Elle est regardée dans sa globalité depuis un point de vue extérieur. Elle se maintient en équilibre, sans support matériel, parce qu'elle se trouve à égale distance de tous les points de la circonférence céleste et qu'elle n'a aucune raison d'aller dans une direction plutôt qu'une autre. Les astres sont assimilés à des trous dans des anneaux remplis d'un feu et entourant entièrement la Terre. Ils peuvent passer sous la Terre et recommencer chaque jour leur course céleste sans jamais l'interrompre. Les anneaux se trouvent à différentes distances de la Terre. L'espace d'Anaximandre reste peu étendu mais il possède de nouvelles caractéristiques. C'est un espace géométrisé : la Terre occupe une place définie relativement à la périphérie, il y a des rapports de distance et de position, les directions sont équivalentes.
La formation du cosmos est expliquée à partir des expériences de la vie courante
Anaxagore est né en Ionie vers 500 av. J.-C. Il vient ensuite s'installer à Athènes où il enseigne pendant une trentaine d'années. D'après Hippolyte [Tannery, réf10, p. 306-307] : « L'ordonnance du ciel résulte du mouvement circulaire ; le dense, l'humide, l'obscur, le froid et, en général, tout ce qui est lourd, s'est réuni vers le milieu et s'y est figé, ce qui a formé la Terre ; les contraires, le chaud, le lumineux, le sec, le léger, se sont portés vers le haut de l'éther. La forme de la Terre est plate ; elle reste suspendue par suite de sa grande largeur et parce qu'il n'y a pas de vide ; l'air est dès lors assez fort pour supporter la Terre. (…) Le Soleil, la Lune et tous les astres sont des pierres incandescentes entraînées par la révolution de l'éther. Le Soleil et la Lune sont au-dessous des astres. (…) La Lune est plus basse que le Soleil et plus voisine de nous. Le Soleil surpasse le Péloponèse en grandeur. La Lune n'a pas de lumière propre ; elle est éclairée par le Soleil. Les astres tournent en passant sous la Terre. Les défaillances de la Lune sont dues à l'interposition de la Terre (…) ; le Soleil s'éclipse aux nouvelles lunes, par suite de l'interposition de la Lune. (…) Anaxagore a le premier déterminé ce qui concerne les éclipses et les phases ; il a dit que la Lune est une terre et qu'elle présente des plaines et des précipices ».
Anaxagore explique la formation du cosmos sans aucune préoccupation d'ordre religieux, sans la moindre référence à des divinités ou à des mythes. Il ne s'appuie que sur l'expérience de la vie courante et fait intervenir les notions du lourd et du léger, du froid et du chaud, de l'humide et du sec. Il rend compte de la manière dont le Monde s'est constitué à l'origine à partir d'exemples simples, souvent empruntés à la vie quotidienne, permettant à chacun de faire le raisonnement. Il y a un idéal d'intelligibilité, un effort pour expliquer la structure du Monde d'une manière purement positive et rationnelle. Le cosmos acquiert des propriétés physiques : les astres sont des pierres incandescentes, la Lune a des plaines et des précipices, le Soleil a une taille réelle qui peut être estimée (même si l'estimation proposée est très petite). Le cosmos prend une certaine consistance, il possède un certain volume : la Terre et la Lune, éclairées par le Soleil, projettent leurs ombres dans l'espace, la Lune peut passer devant le Soleil ou derrière la Terre, elle change d'aspect en fonction de sa position relative au Soleil et à la Terre.
Le cosmos acquiert une profondeur
La vie de Philolaos (v. 450 – v. 400 av. J.-C.) n'est pas bien connue. Il est probable que c'est lui qui rende public et qui mette par écrit un certain nombre de connaissances de l'école pythagoricienne, gardées jusque là plus ou moins secrètes. D'après Aétius [in Chaignet, réf3] : « Philolaüs a mis le feu au milieu, au centre : c'est ce qu'il appelle la Hestia du Tout, la maison de Jupiter et la mère des Dieux, l'autel, le lien, la mesure de la nature. En outre il pose encore un second feu, tout-à-fait en haut, et enveloppant le monde. Le centre, dit-il, est par sa nature le premier ; autour de lui les dix corps divers accomplissent leurs choeurs dansants ; ce sont le ciel, les planètes, plus bas le soleil, au-dessous de celui-ci la lune ; plus bas la Terre, et au-dessous de la Terre, l'anti-Terre, et enfin au-dessous de tous ces corps, le feu Hestia, au centre, où il maintient l'ordre. La partie la plus élevée de l'Enveloppant, dans laquelle il prétend que les éléments se trouvent à l'état parfaitement pur, il l'appelle l'Olympe ; l'espace au-dessous du cercle de révolution de l'Olympe, et où sont rangés en ordre les cinq planètes, le soleil et la lune, forme le Monde, Cosmos ; enfin au-dessous de ces derniers corps est la région sublunaire, qui entoure la Terre, et où se trouvent les choses de la génération, amie du changement : c'est le Ciel. L'ordre qui se manifeste dans les phénomènes célestes, est l'objet de la science ; le désordre qui se manifeste dans les choses du devenir est l'objet de la vertu : l'une est parfaite, l'autre imparfaite ».
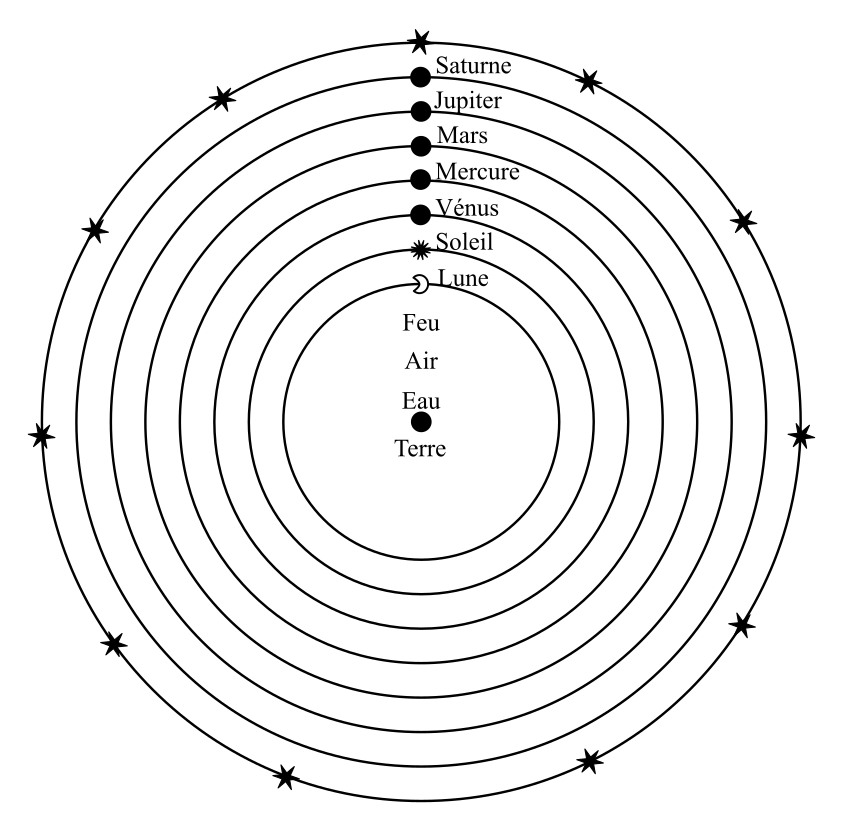
Certains aspects du modèle de Philolaos nous paraissent extravagants, en particulier le feu central et l'anti-Terre, dont on ne perçoit pas bien l'utilité (Figure 1). Mais d'autres aspects sont visionnaires. La Terre, délogée du centre du Monde, est en mouvement au sein d'un espace semblable au nôtre. Certes le corps qui occupe la place centrale de cet espace n'est pas fixé et sera fortement discuté par la suite : le feu pour Philolaos, la Terre pour les partisans du géocentrisme, le Soleil pour les défenseurs de l'héliocentrisme. De même, l'ordre des astres ne paraît pas parfaitement défini. Mais le cadre dans lequel les diverses hypothèses cosmologiques vont pouvoir être proposées est dorénavant posé : le domaine terrestre, situé en deçà de la Lune est nettement séparé du domaine céleste ; les astres sont différenciés ; ils sont situés à différentes distances du centre et tournent en cercle autour de lui. L'espace des mythologies laisse définitivement la place à un cosmos ayant une certaine profondeur.
Figure 1. Représentation schématique du modèle cosmologique de Philolaos
L'ordre des planètes ne parait pas fixé.
Le cosmos a une forme sphérique
Si les philosophes d'Ionie cherchent à rendre compte de la formation physique du cosmos, l'école pythagoricienne s'intéresse plus à sa géométrie. Il semble que ce soit au sein de cette école que les premières conceptions sphériques du Monde sont développées. Parménide (v. 515 – ap. 450 av. J.-C.), qui vit en Italie du Sud au tournant du VIe et du Ve siècle, affirme que la Terre est sphérique et Oenopide (v. 490 – v. 420 av. J.-C.), dont la vie couvre le milieu du Ve siècle, approfondit l'étude mathématique de la sphère céleste. La sphéricité du cosmos apparait également chez Philolaos. Les motivations sont essentiellement d'ordre esthétique et philosophique, la sphère étant la forme la plus belle, la plus parfaite. Ces idées se retrouvent plus tard chez Platon (428 – 348 av. J.-C), qui est un élève de Socrate et un des plus grands philosophes de la Grèce antique. Il avance [Platon, réf7, Timée, 33b, p.414] : « C'est pourquoi le dieu a tourné le monde en forme de sphère, dont les extrémités sont partout à égale distance du centre, cette forme circulaire étant la plus parfaite de toutes et la plus semblable à elle-même, car il pensait que le semblable est infiniment plus beau que le dissemblable ». Ou encore [Platon, réf6, p. 207] : « Ma conviction à moi [c'est Socrate qui parle], c'est en premier lieu, que, si la terre est au centre du monde et avec la forme d'une sphère, elle n'a besoin, pour ne pas tomber, ni de l'air, ni d'aucune autre semblable résistance ; mais il y a assez pour la maintenir, de la similitude, en tous les sens, du monde avec lui-même ».
Platon reprend l'idée d'Anaximandre selon laquelle la Terre se tient en équilibre au centre du Monde par indifférence. Les deux citations données peuvent laisser croire que les arguments avancés restent uniquement d'ordre esthétique. Ce n'est plus le cas. À l'époque de Platon, de nombreux faits d'observation viennent confirmer l'intuition philosophique de la sphéricité du Monde. En effet, si la forme sphérique du Ciel ne peut pas être perçue à partir de la simple vue des phénomènes, elle peut l'être, en revanche, à partir de l'observation du mouvement des astres, en particulier des étoiles circumpolaires (voir la citation de Ptolémée, un savant du IIe siècle ap. J.-C., donnée en fin d'article). Au cours de la nuit, ces dernières décrivent autour du pôle céleste immobile des arcs de cercle d'autant plus grands qu'elles sont plus éloignées du pôle céleste (Figure 2). Les étoiles paraissent toutes appartenir à une même sphère enveloppant la Terre et tournant en bloc. De la même manière, la forme sphérique de la Terre est corroborée par les changements d'aspect du Ciel étoilé qui s'offrent à la vue des voyageurs. Les savants grecs ne peuvent ignorer qu'à Chypre et en Égypte, on voit apparaitre de nouvelles étoiles, invisibles lorsqu'on se trouve à Athènes ou en Thrace ou que d'autres étoiles se lèvent et se couchent, alors que plus au Nord elles sont circumpolaires. Cette variation dans l'apparence du Ciel est la preuve que la Terre est courbée dans la direction Nord-Sud. Il n'existe pas d'observation aussi évidente pour confirmer la courbure Est-Ouest, mais les raisons de symétrie s'imposent.
L'avènement du géocentrisme : Eudoxe et Aristote
Les spéculations cosmologiques du VIe et du Ve siècles av. J.-C. sont disparates et sources de polémiques : quelle est la place de la Terre, quelle est sa forme, a-t-elle un mouvement ? Elles préparent les travaux d'Eudoxe (409 – 356 av. J.-C.) et d'Aristote (384 – 322 av. J.-C.) qui vont trancher parmi les hypothèses proposées et promouvoir le géocentrisme.
Le cosmos géométrique d'Eudoxe
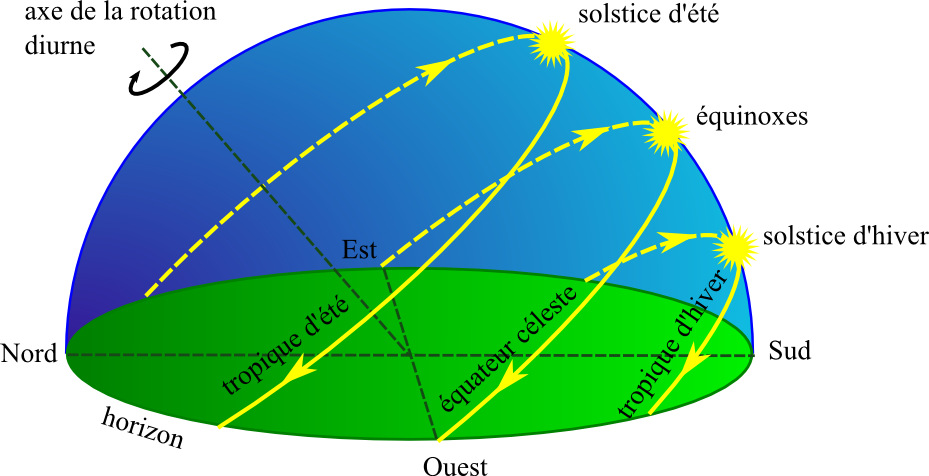
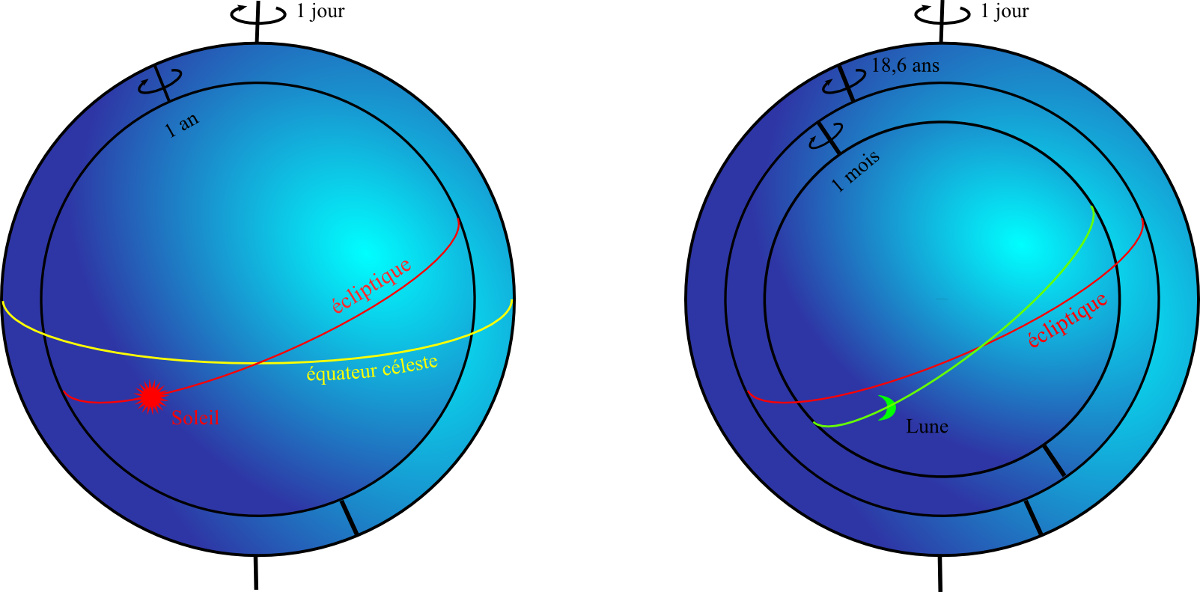
L'assimilation de la Terre et du Ciel à des sphères présente l'énorme avantage d'autoriser un traitement géométrique des problèmes astronomiques. Le premier à en comprendre toute la portée est Eudoxe. Ce dernier vit à une époque intermédiaire entre Platon et Aristote et représente une figure majeure de l'astronomie ancienne. Il propose la première théorie cinématique expliquant le déplacement des astres dans le Ciel. Son idée, sans doute empruntée à Platon, consiste à décomposer le mouvement complexe d'un astre en une somme de mouvements simples. Pour chaque astre, Eudoxe utilise un système indépendant de sphères emboîtées, centrées sur la Terre et solidaires les unes des autres. Chaque sphère tourne uniformément autour de son axe respectif et communique son mouvement à la sphère située immédiatement sous elle ; l'astre étant fixé à la sphère la plus intérieure. Pour le Soleil, deux sphères suffisent. La première tourne sur elle-même d'Ouest en Est en un jour pour reproduire le mouvement diurne, tandis que la deuxième effectue sa révolution en une année dans le sens opposé à la première avec un axe incliné pour reproduire le déplacement du Soleil le long de l'écliptique (Figure 5). Le mouvement résultant du Soleil consiste en une sorte de spirale montante puis descendante, encadrée par les deux tropiques. Pour la Lune, une troisième sphère est nécessaire pour rendre compte de la rotation de l'orbite de la Lune qui tourne autour de l'axe de l'écliptique en 18,6 ans tout en conservant une inclinaison constante de 5° sur l'écliptique. De la même manière, des sous-systèmes indépendants de sphères emboîtées homocentriques permettent d'expliquer le mouvement des planètes, le nombre de sphères requis étant simplement plus important.
Le cosmos physique d'Aristote
L'approche d'Aristote est très différente. Il réfléchit en physicien et critique les diverses opinions cosmologiques émises par ses prédécesseurs en présentant les arguments pour départager le vrai, le vraisemblable et le faux. Il considère qu'il existe une différence fondamentale entre le domaine situé au-delà de l'orbite lunaire (le monde supralunaire - Lune comprise) et le domaine situé en deçà de l'orbite lunaire (le monde sublunaire). Le domaine supralunaire est rempli par l'éther. C'est le domaine des astres, des mouvements cycliques et permanents, immuables et parfaits. Il ne subit aucune altération, aucune variation et est animé uniquement par des mouvements circulaires uniformes, qui ne connaissent ni début, ni fin. Les astres tournent parce que c'est la nature de l'éther de tourner en rond. Au contraire, le domaine sublunaire, constitué à partir des quatre éléments (terre, eau, air et feu) et de leur combinaison, est celui des changements et des transformations continuelles. Il est structuré par l'opposition lourd-léger. Selon Aristote, chacun des quatre éléments a un lieu naturel, dans lequel il peut demeurer en repos dans toute sa perfection : la Terre occupe la position la plus basse, puis vient l'eau, l'air et le feu. Chacun des quatre éléments possède également un mouvement naturel de translation rectiligne par lequel il regagne son lieu naturel lorsqu'il en a été séparé par violence : les lourds (la terre et l'eau) vont vers le centre de la Terre, confondu avec le centre de l'univers ; les légers (l'air et le feu) se dirigent vers la périphérie du monde sublunaire. Les éléments possèdent une qualité intrinsèque qui leur permet de regagner leur lieu pour rétablir à chaque instant la disposition naturelle et l'ordre du Monde.
Aristote affirme que la Terre se tient immobile au centre du Monde car le mouvement naturel des parties de la Terre aussi bien que de la Terre elle-même prise comme un tout tend vers le milieu du Monde. Il rejette donc l'argument d'indifférence d'Anaximandre et de Platon pour promouvoir une raison physique. C'est parce que le centre de la Terre est uni au centre du Monde que l'équilibre de la Terre est vérifié. Pour prouver l'immobilité de la Terre, il avance l'argument suivant [Aristote, réf1, II, 14, 296b, p. 287] : « Il est donc manifeste que la Terre est nécessairement au centre et immobile (…) parce que les projectiles pesants envoyés vers le haut en ligne droite reviennent au même point, et le feraient même si la force les projetait à l'infini ». Si la Terre tournait, un objet lancé verticalement en l'air ne pourrait pas retomber au point de départ mais il devrait retomber bien à l'Ouest du point initial car pendant son trajet aérien le sol se déplacerait vers l'Est rapidement sous lui[2]. Cet argument sera pendant très longtemps opposé aux partisans du mouvement diurne de la Terre jusqu'à ce que Galilée le réfute et explique sa non-validité au début du XVIIe siècle.
Pour prouver la sphéricité de la Terre, Aristote présente un argument physique : la tendance vers le bas de chaque portion de terre amène une agglomération, un tassement et une compression qui imposent que la Terre dans son ensemble ait sensiblement la forme régulière et symétrique de la sphère. Il ajoute également des indices sensibles de la sphéricité (voir la citation d'Aristote donnée en fin d'article) : lors des éclipses de Lune, l'ombre de la Terre projetée sur la Lune a une forme circulaire, ce qui ne peut être le cas que si la Terre est sphérique (cf., par exemple, Éclipse totale de Lune dans la nuit du 20 au 21 décembre 2010...) ; un déplacement même faible vers le Nord ou le Sud à la surface du globe amène un changement dans la configuration du Ciel. Ces indices prouvent également la taille modeste de notre planète relativement à l'Univers : la Terre n'est qu'un point devant les dimensions de la sphère des étoiles fixes et l'observateur, quelque soit sa position à la surface de la Terre, voit toujours les phénomènes célestes comme s'il était placé exactement au centre du Monde (en langage moderne, nous dirions que la parallaxe diurne est insensible).
Autour de la Terre, dans le domaine supralunaire, se trouvent la Lune, le Soleil et les planètes. Aristote discute de leurs places respectives en s'appuyant sur les travaux des astronomes de son temps. Le principe communément accepté est qu'une planète est d'autant plus éloignée de la Terre que sa période sidérale est grande. La place du Soleil, de Mercure et de Vénus reste incertaine mais si l'on suit Platon, l'ordre supposé est le suivant : la Lune, le Soleil, Vénus, Mercure, Mars, Jupiter et Saturne (Figure 6). Pour rendre compte du mouvement des astres, Aristote reprend le système des sphères homocentriques d'Eudoxe avec les améliorations proposées par Callippe (IVe siècle av. J.-C.). Mais pour Aristote, les sphères ne sont pas des simples entités mathématiques, elles ont une existence physique, matérielle. Elles sont réelles, elles portent et entraînent les astres qui y sont fixés. Le système des sphères ne représente pas pour lui une modélisation mathématique du Monde mais une description physique.
Le Cosmos d'Aristote est parfaitement agencé. C'est un espace structuré en couches concentriques selon la théorie des lieux naturels. On peut retenir quatre idées principales :
- la théorie des lieux et des mouvements naturels entérine un clivage essentiel entre la Terre et le Ciel ;
- la Terre sphérique est immobile et coïncide avec le centre du Monde ;
- le Monde est clos et sphérique ;
- les astres sont portés par des sphères matérielles, qui ont naturellement un mouvement de rotation uniforme.
C'est la solidité du soubassement cosmologique, de la conception de l'univers qui assure la validité des conceptions physiques d'Aristote et, en retour, ce sont les principes de la physique qui garantissent la stabilité et l'harmonieuse disposition du Monde. Cosmologie et physique sont parties liées pour proposer une conception unifiée et cohérente du Monde. Cette dernière servira de fondement pendant de longs siècles à toutes les discussions astronomiques et cosmologiques.
Figure 4. Représentation schématique du modèle cosmologique d'Aristote
Les planètes sont rangées selon l'ordre de Platon.
Des modèles cosmologiques alternatifs
Le système géocentrique prôné par Eudoxe et Aristote s'impose au cours du IVe siècle av. J.-C. comme la représentation dominante du Monde. Les discussions sont cependant nombreuses et d'autres modèles cosmologiques sont proposés même s'ils ne remportent pas l'adhésion. Trois points sont discutés. Le premier concerne la rotation journalière du Ciel. Les savants de l'époque sont pleinement conscients de la relativité du mouvement : lorsqu'un objet se déplace relativement à un observateur et qu'aucun point de référence extérieur n'est disponible, on ne peut pas savoir si c'est la chose vue qui se déplace, ou l'observateur ou encore un mélange des deux. Si l'on s'en tient aux apparences, il est impossible de trancher entre, d'une part, un mouvement journalier du Ciel et une Terre fixe et, d'autre part, un mouvement journalier de la Terre et un Ciel fixe. Pour départager les deux situations, il faut recourir à d'autres arguments. Les partisans d'Aristote affirment que l'immobilité de la Terre est prouvée par toute la cosmologie d'Aristote et par le fait que si la Terre tournait alors les mouvements à la surface du globe seraient très perturbés. Les détracteurs pointent certaines contradictions dans le système géocentrique. Si la Terre est supposée immobile, il est nécessaire que les étoiles soient situées à une distance finie pour pouvoir boucler le tour du Ciel en une journée. En effet, si elles étaient à l'infini, elles devraient parcourir des distances infinies à des vitesses complètement déraisonnables. Mais si le Monde est fini et clos, comment contrer l'argument déjà présenté par Archytas de Tarente (428 – 347 av. J.-C.) : le savant arrivé à la limite du Monde, peut-il percer la voûte de son bâton pour atteindre l'extérieur (Figure 7) ? Et si oui, quel extérieur : le vide, le non-être ? Il n'est pas impossible que ce soient ces réflexions qui aient amené Hicétas et Ecphantus, deux pythagoriciens du début du IVe siècle av. J.-C., à affirmer la rotation axiale diurne de la Terre. Dans ce cas, les étoiles sont immobiles et peuvent se situer à l'infini : le Monde n'a plus de limite extérieure. L'idée de la rotation axiale de la Terre est aussi reprise par Héraclide du Pont (v. 388 – v. 315 av. J.-C.), qui est l'exact contemporain d'Aristote.
Source - © 1993 Gravure coloriée par Blandine Lemoine d'après original au Deutsches Museum, Munich coll. Carmen
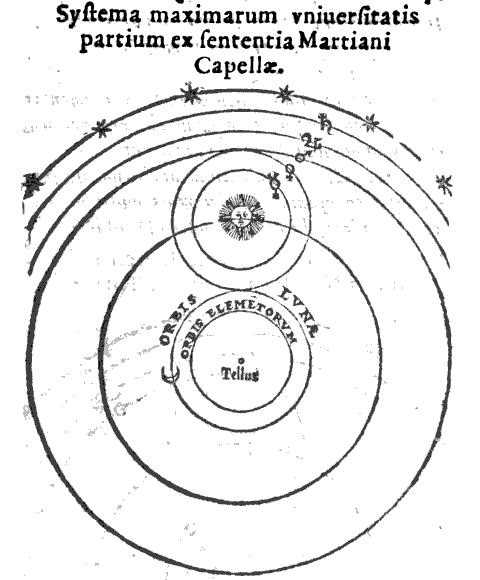
Un deuxième point, discuté également par Héraclide, porte sur le mouvement des planètes. Sept corps se distinguent des étoiles : la Lune, le Soleil et les cinq planètes visibles à l'œil nu (Mercure, Vénus, Mars, Jupiter et Saturne). Mais les cinq planètes n'ont pas un comportement similaire. D'un côté, Mercure et Vénus restent toujours dans la proximité du Soleil. Elles sont visibles soit le matin dans la partie Est du Ciel avant le lever du Soleil, soit le soir dans la partie Ouest du Ciel après le coucher du Soleil. Elles semblent toujours suivre ou précéder le Soleil. D'un autre côté, Mars, Jupiter et Saturne s'écartent du Soleil et peuvent être visibles au milieu de la nuit. Comment expliquer cette différence de comportement ? Héraclide propose une solution étonnante : Vénus et Mercure tournent autour du Soleil, qui est lui-même en orbite avec la Lune, Mars, Jupiter et Saturne autour de la Terre (Figure 8). C'est un système partiellement héliocentrique, qui connait un certain succès. Il n'est jamais mis entièrement de côté et est connu au Moyen-Âge.
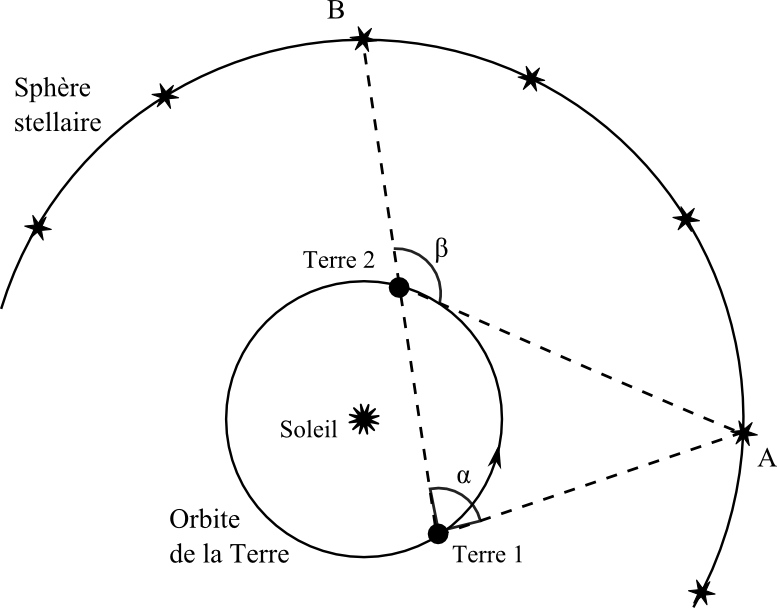
Le dernier point concerne la place de la Terre. Aristarque de Samos (env. 310 – env. 230 av. J.-C.), connu pour avoir estimé la taille de la Lune et du Soleil et leur distance à la Terre à partir d'une très belle analyse géométrique, propose un système héliocentrique. Dix-huit siècles avant Copernic, il avance que la Terre est en rotation sur elle-même en une journée et en révolution autour du Soleil en une année. Pour Aristarque, la Terre n'est donc pas au centre du Monde. Cette option n'a pratiquement rencontré aucun écho avant Copernic car elle se heurte à une difficulté très sérieuse. Si la Terre tourne autour du Soleil, alors deux étoiles distantes l'une de l'autre ne peuvent pas être vues sous le même angle depuis la Terre tout au long de l'année (Figure 9). Il s'agit de ce que nous nommons aujourd'hui la parallaxe annuelle (qui ne sera observée pour la première fois qu'en 1838 par Bessel). Puisque les étoiles conservent des positions fixes les unes par rapport aux autres et qu'aucune déformation périodique des constellations n'est observée, il est certain que la Terre ne se déplace pas relativement aux étoiles. La seule autre alternative est de considérer que les étoiles sont beaucoup plus éloignées qu'on le croit. C'est ce que propose Aristarque mais la solution paraît inadmissible. Il faudrait supposer que ce n'est plus seulement la Terre qui n'est qu'un point relativement à la sphère des étoiles fixes, ce que tout le monde accepte, mais également l'orbite de la Terre autour du Soleil, ce qui parait complètement absurde. L'éloignement des étoiles bien au-delà des planètes est inenvisageable.
Figure 6. Le système partiellement héliocentrique d'Héraclide (par Valentin Naboth, 1573) | Pour que cet effet soit imperceptible, il faut que l'orbite de la Terre soit très petite devant les dimensions de la sphère stellaire, ce qui parait inenvisageable pendant l'Antiquité. |
L'astronomie quantitative d'Hipparque et de Ptolémée
L'astronomie d'Eudoxe et d'Aristote est une astronomie qualitative et explicative. Elle rend compte du mouvement des astres dans le Ciel et de la structure du cosmos sans proposer de calculs. Avec Hipparque (IIe siècle avant J.-C.) et Ptolémée (IIe siècle après J.-C.), qui sont les deux plus grands astronomes de l'Antiquité, l'astronomie grecque, en particulier celle d'Alexandrie dans le cas de Ptolémée, évolue. Elle s'appuie toujours sur les principes cosmologiques d'Aristote (voir les citations de Ptolémée -mouvement du ciel et Terre immobile- données en fin d'article) mais écarte le système des sphères homocentriques d'Eudoxe pour le remplacer par le système des épicycles et des excentriques, peut-être inventé par Apollonios (v. 262 – v. 190 av. J.-C.). Le système d'Eudoxe était ingénieux mais il obligeait les planètes à se déplacer à une distance constante de la Terre. Or la variation d'éclat des planètes montre que leur distance à la Terre est variable. Le système des épicycles et des excentriques autorise une variation des distances et surtout il rend possible une approche quantitative, permettant de prédire la position des astres dans le Ciel.
Les épicycles et les excentriques
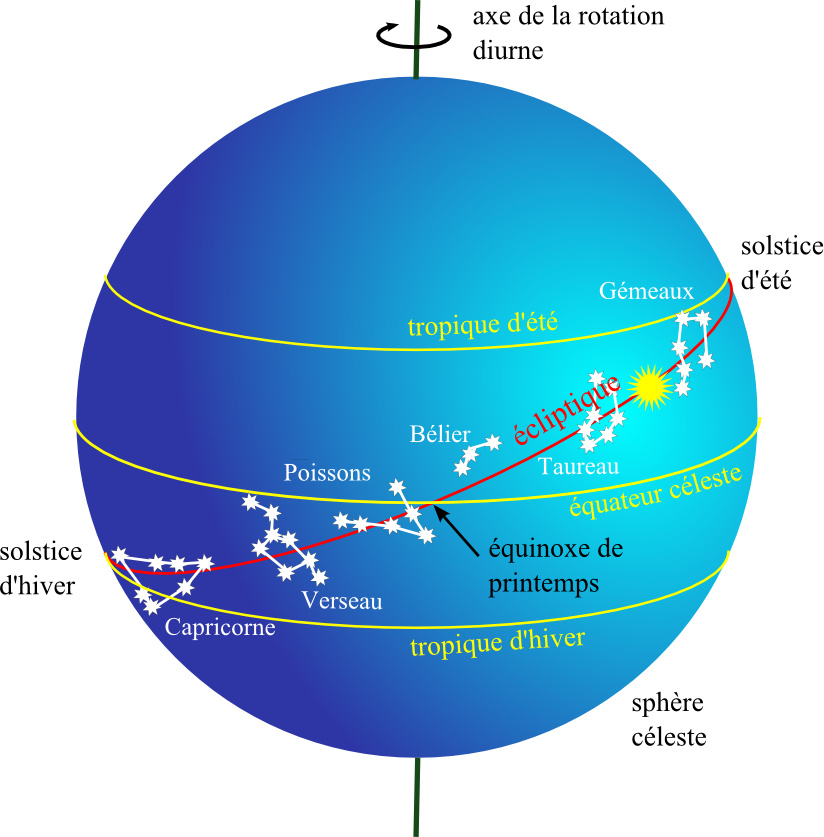
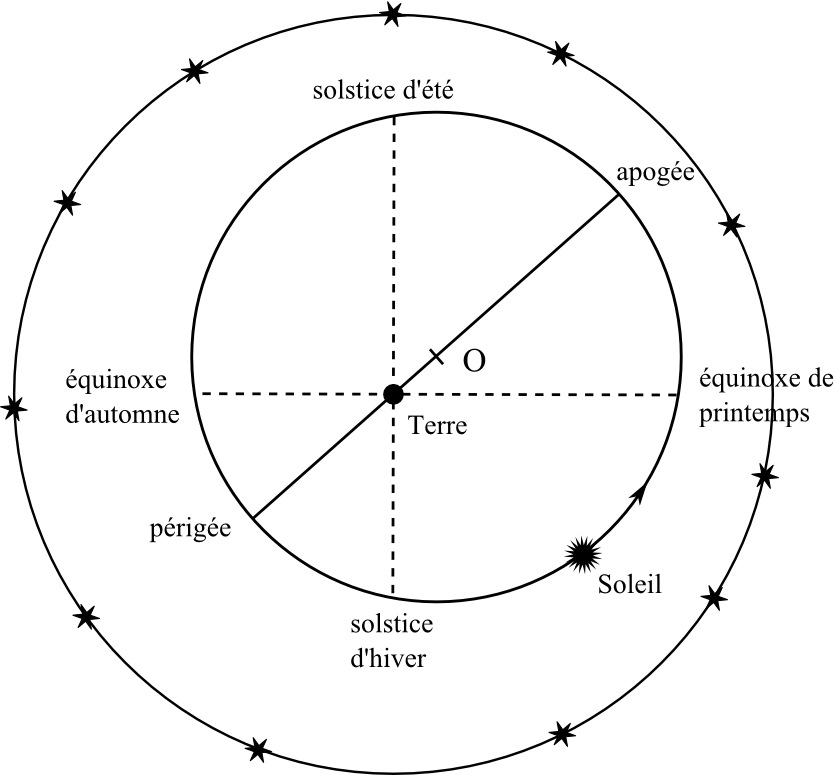
Nous allons montrer l'application du système des épicycles et des excentriques au Soleil et aux planètes. Le but est de rendre compte, non pas du mouvement diurne des astres, mais de leur mouvement additionnel par rapport aux étoiles. Pour le Soleil, le problème est le suivant. Le Soleil décrit l'écliptique en une année et passe par quatre positions remarquables : au moment de l'équinoxe de printemps il est situé dans le plan de l'équateur, au moment du solstice d'été il est au plus haut au-dessus de l'équateur, au moment de l'équinoxe d'automne il est à nouveau dans l'équateur et au moment du solstice d'hiver il est au plus bas au-dessous de l'équateur. Le temps que met le Soleil pour passer d'une position à la suivante définit les saisons astronomiques et à chaque fois, le Soleil a dû tourner de 90° par rapport à la Terre. Or les saisons n'ont pas une durée égale : pendant l'Antiquité, le printemps est la saison la plus longue avec 94,0 jours et l'automne, la saison la plus courte avec 88,6 jours. Cela implique que, vu depuis la Terre, le Soleil se déplace parmi les étoiles avec une vitesse variable ! Comment expliquer ce fait déconcertant ? Une solution simple consiste à supposer que le Soleil décrit un cercle avec une vitesse constante mais que le centre O de ce cercle n'est plus confondu avec la Terre (le centre du Monde). Le Soleil décrit un excentrique (Figure 10). Le décalage optique de la Terre explique que le Soleil tourne autour de la Terre avec une vitesse variable tout en permettant de conserver la contrainte, pour ne pas dire le dogme, du mouvement circulaire uniforme.
Figure 8. Mouvement excentrique du Soleil
La Terre est décalée par rapport au centre O du cercle décrit par le Soleil.
Pour les planètes, le problème est celui de leur rétrogradation. Chaque jour, les planètes font un tour complet du Ciel (mouvement diurne) mais en plus elles se décalent peu à peu par rapport aux étoiles, ce qui permet de les distinguer. La plupart du temps, les planètes se déplacent vers l'Est par rapport aux étoiles comme le Soleil mais de temps en temps, elles changent de sens et se déplacent vers l'Ouest, avant de reprendre un déplacement vers l'Est : elles ont effectué une "boucle" de rétrogradation (Figure 11). D'une manière étonnante, le mouvement des planètes, vu depuis la Terre, est lié au mouvement du Soleil. Le lien est évident pour les planètes inférieures (Mercure et Vénus), qui restent toujours dans la proximité du Soleil. Mais un lien existe également pour les planètes supérieures (Mars, Jupiter et Saturne) : elles effectuent toujours leur rétrogradation lorsqu'elles sont en opposition avec le Soleil (lorsqu'elles rétrogradent, elles se lèvent approximativement lorsque le Soleil se couche). Ces liens ne sont pas pris en considération pendant toute l'Antiquité et ne prendront sens qu'avec la théorie héliocentrique de Copernic.
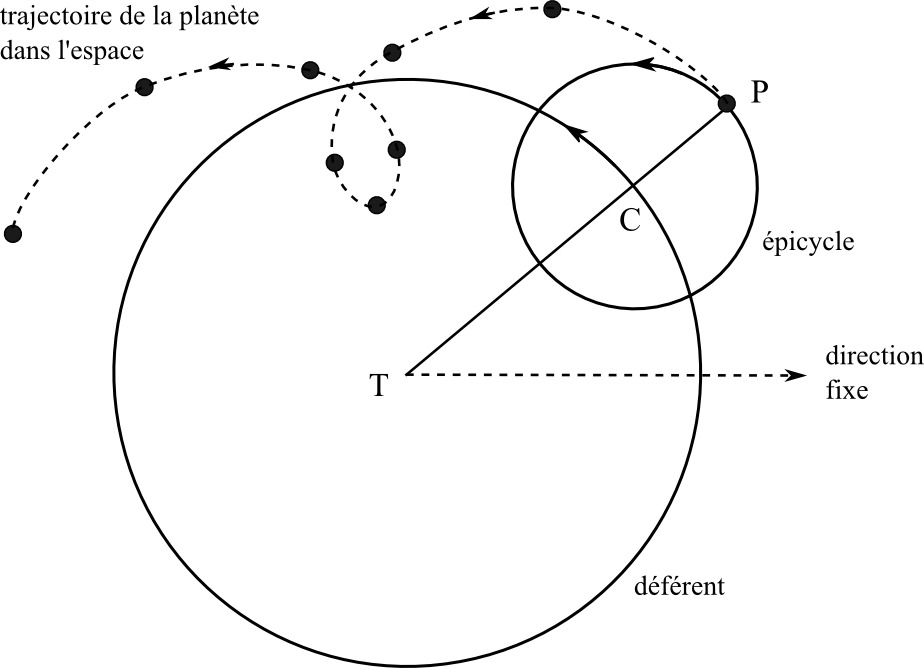
Pour expliquer le mouvement complexe des planètes, un premier modèle peut être proposé : la planète P parcourt avec une vitesse uniforme un petit cercle, l'épicycle, dont le centre C décrit lui-même avec une autre vitesse uniforme un second cercle, le déférent, centré sur la Terre T (Figure 12). Si les rayons de l'épicycle et du déférent ainsi que les vitesses de rotation sont convenablement choisis, la combinaison des deux mouvements uniformes permet d'expliquer les rétrogradations des planètes. Ce premier modèle n'est pas suffisant car il possède un défaut grave : pour une planète donnée, il crée des boucles de rétrogradations qui sont toutes identiques et qui se répètent toutes au bout d'un intervalle de temps constant. Or les rétrogradations ne sont ni régulières en amplitude, ni régulières dans le temps. Ptolémée propose deux aménagements : le déférent est lui même un excentrique (la Terre est décalée par rapport au centre O du déférent) et le centre C de l'épicycle se déplace uniformément, non plus par rapport au centre O du déférent mais par rapport à un point équant E, symétrique de la Terre T par rapport à O (Figure 13). C'est à ce prix que la position des planètes peut être retrouvée d'une manière tout à fait satisfaisante, c'est-à-dire d'une manière cohérente avec la précision des observations de l'époque.
Source - © 2016 J.-M. Vienney, Cahiers Clairaut 156 Figure 9. La rétrogradation de Mars en 2016 Montage photographique réalisé par superposition de 79 images prises d'avril (à droite) à juin 2016 (à gauche). On observe aussi la trajectoire de Saturne sur la gauche du montage. Voir aussi Les boucles de rétrogradation de Mars, par Pierre Causeret (Cahiers Clairaut). | |
Figure 10. Mouvement épicyclique d'une planète La planète P décrit l'épicycle de centre C. Le centre C décrit le déférent dont le centre est la Terre T. | Figure 11. Les théories planétaires de Ptolémée La Terre T est excentrée par rapport au centre O du déférent et le mouvement uniforme du centre C de l'épicycle s'effectue par rapport au point équant E. |
Épicycle et "épicycle"
par Pierre Thomas (ENS de Lyon)
On peut noter que l'introduction des épicycles a été une "astuce" pour ne pas sortir du "dogme" selon lequel « les mouvements des astres sont toujours circulaires et uniformes », même si cette "astuce" a abouti à un modèle physique complexe mathématiquement quantifiable. Le mot "épicycle" prend parfois le sens limité d'"astuce" lorsqu'il s'agit de sauver un modèle de pensée. Il est, en effet, souvent plus facile, intellectuellement parlant, de rajouter des causes de second ordre (comme les épicycles) pour expliquer des données qui sortent légèrement du modèle couramment admis que de changer de modèle. Quand des données nouvelles s'écartent du modèle en vigueur et qu'elles sont bien vérifiées, soit on modifie le modèle, soit on néglige ces données, soit on rajoute ce qui peut être considéré comme l'équivalent d'un épicycle. Cette dernière attitude est assez fréquente chez ceux qu'on pourrait qualifier de scientifiques "conservateurs". Par exemple, quand on a découvert, à la fin des années 1990, que l'expansion de l'Univers s'accélérait au lieu de ralentir comme le voulait le modèle standard, on a rajouté ce qu'on appelle maintenant l'Énergie Sombre. Au moins jusqu'aux résultats du satellite Planck en 2013, certains pensaient que cette Énergie Sombre n'était qu'un "épicycle" pour sauver le modèle standard.
L'interprétation cosmologique
Ptolémée expose le système des épicycles et des excentriques dans son ouvrage, la Syntaxe mathématique, plus connue sous son nom arabisé, l'Almageste. Le point de vue développé est uniquement géométrique et cinématique : le mouvement des planètes est reconstitué à partir de combinaisons d'épicyles et d'excentriques sans interrogation sur la réalité du système. Dans un second traité, Hypothèses sur les planètes, Ptolémée passe de la modélisation mathématique à la modélisation physique. Le but n'est plus de calculer la position des astres mais de proposer une maquette réaliste du Monde.
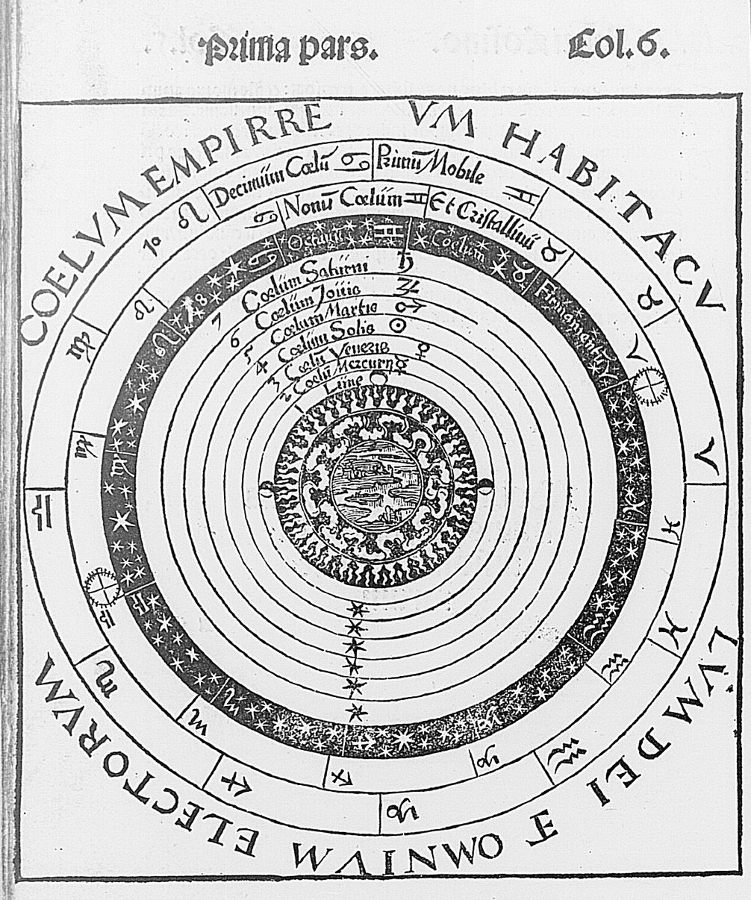
Dans l'Almageste, le système expliquant le mouvement de chaque planète est élaboré indépendamment des autres, le seul lien étant la direction du Soleil. Le rapport entre le rayon du déférent sur le rayon de l'épicycle peut être déterminé pour chaque planète mais il n'est pas possible de connaître la valeur absolue de ces deux rayons. On ne peut donc pas les comparer d'une planète à l'autre. Rien ne permet la détermination ni de l'ordre des planètes, ni de leur distance à la Terre. Dans ses Hypothèses sur les planètes, Ptolémée est obligé de prendre partie pour un certain nombre de propositions arbitraires. Pour l'ordre, Ptolémée propose que la Lune est l'astre le plus proche de la Terre puis vient Mercure, Vénus, le Soleil, Mars, Jupiter et Saturne (Figure 14). Le Soleil sépare les planètes qui toujours l'accompagne (Mercure et Vénus) de celles qui s'en écartent (Mars, Jupiter et Saturne). Pour les distances, il a la conviction que l'univers ne peut comporter aucune espace vide et dépourvu d'utilité et que chaque système planétaire doit suivre immédiatement le précédent. Il divise l'univers en zones concentriques contigües, appelées sphères planétaires. Ces sphères ont une existence matérielle. Elles possèdent une certaine épaisseur permettant aux planètes de se mouvoir en leur sein, entraînées sur leurs excentriques et leurs épicycles par d'autres corps matériels. Les sphères sont limitées par deux surfaces concentriques au Monde. La première, la plus à l'intérieur, correspond à la position de la planète à son périgée ; la seconde, la plus à l'extérieur, à la position de la planète à son apogée. Et puisque le vide n'existe pas, la surface extérieure d'une sphère coïncide avec la surface intérieure de la sphère suivante. Avec ce procédé, Ptolémée estime que le rayon de la sphère des étoiles qui clôt le monde, est de 20 000 rayons terrestres. Comme il considère que la circonférence de la Terre est de 180 000 stades égyptiens et qu'un stade égyptien est d'environ 150 mètres, la taille du cosmos vaut environ 90 millions de kilomètres (pour fixer les idées, rappelons que la distance Terre – Soleil est en réalité de 150 millions de kilomètres).
Source - © 1524 D'après Petrus Apianus, Cosmographicus liber, Gallica, BnF
Figure 12. Le système géocentrique de Ptolémée
Les modèles mathématiques et physiques des savants arabes
L'Almageste de Ptolémée est une œuvre grandiose, qui synthétise l'ensemble des connaissances astronomiques grecques. C'est par elle que l'astronomie grecque est transmise aux savants arabes à la fin du VIIIe siècle puis aux savants latins au XIIe siècle. Ptolémée prétend que son modèle mathématique (qui est performant) est également un modèle physique, qui décrit exactement les mouvements réels de corps réels et qui révèle la structure véritable du cosmos. Les savants arabes prennent cette prétention au sérieux mais mettent en évidence des contradictions importantes dans les modèles de Ptolémée. Ces dernières proviennent principalement du point équant, qui constitue une entorse sévère au principe du mouvement circulaire uniforme. Si les sphères qui portent les planètes sont réelles alors l'équant impose à une sphère de tourner uniformément autour d'un axe qui ne passe pas par son centre, ce qui est physiquement impossible ! Une grande partie du travail des savants arabes consiste à élaborer de nouveaux modèles mathématiques qui restent géocentriques mais qui ne sont pas incohérents avec la réalité physique qu'ils décrivent. Ils déploient une très grande ingéniosité pour mettre au point de nouveaux artifices mathématiques qui ne sont pas en contradiction avec les principes cosmologiques d'Aristote.
Ce n'est qu'à la toute fin de la période faste de l'astronomie arabe, au XVIe siècle, qu'al-Khafrī (mort en 1550) interroge la pertinence de l'adéquation entre la modélisation mathématique et la réalité physique. Saliba présente l'intérêt de son approche [Saliba, réf9, p.339, traduction libre] : « En travaillant sur des modèles mathématiques alternatifs qui pourraient remplacer ceux de Ptolémée et en analysant attentivement le travail de ses prédécesseurs qui tous cherchaient des modèles mathématiques uniques pour décrire d'une manière cohérente les phénomènes physiques, cet astronome réalisa finalement qu'un modèle mathématique ne détenait pas en lui-même une vérité physique et qu'il était simplement un autre langage avec lequel on pouvait décrire la réalité physique observée. Il réalisa également que les phénomènes spécifiques qui étaient décrits par les modèles de Ptolémée n'avaient pas des solutions mathématiques uniques respectant les mêmes contraintes. Au contraire, plusieurs modèles mathématiques pouvaient rendre compte des observations de Ptolémée, conduisant à des résultats prédictifs identiques (c'est-à-dire rendant compte des observations aussi bien que Ptolémée l'avait fait) et respectant encore les critères de cohérence imposés par la cosmologie aristotélicienne ». Au moment où al-Khafrī comprend qu'un modèle mathématique pertinent n'a pas forcément un sens physique, les savants occidentaux bouleversent la représentation du Monde avec la conception héliocentrique, qui est le sujet d'un second article : Du géocentrisme à l'héliocentrisme.
Articles suivants de la série « La structure du Monde » :
Bibliographie citée et complémentaire
Aristote, 2004. Traité du Ciel, trad. C. Dalimier et P. Pellegrin, Paris, Flammarion, 465p.
G. Aujac, 1993. Claude Ptolémée. Astronome, astrologue, géographe, Paris, CTHS, 427p.
A. Chaignet (Éd.), 1874. Pythagore et la philosophie pythagoricienne, Paris, Didier et Cie, 402p., En ligne, le livre et les fragments de Philolaos
J. Gapaillard, 1993. Et pourtant, elle tourne !, Paris, Seuil, 347p.
M.P. Lerner, 2008. Le Monde des Sphères, tome I - Genèse et triomphe d'une rprésentation cosmique, 2nde éd., Paris, Les Belles Lettres, 402p.
Platon, 1950. Apologie de Socrate, Criton, Phédon, trad. L. Robin et M.-J. Moreau, Paris, Gallimard
Platon, 1969. Sophiste, Politique, Philèbe, Timée, Critias, trad. E. Chambry, Paris, Garnier-Flammarion, 512p. (BnF-gallica)
R. Rashed, 1997. Histoire des sciences arabes, tome I, Paris, Seuil, 376p.
G. Saliba, 2000. Arabic versus Greek Astronomy: A Debate over the Foundations of Science, Perspective on Sciences, 8, 4, 328-341
P. Tannery,1887. Pour l'histoire de la science hellène, Paris, Gauthier-Villars (Réédition Paris 1930, J. Gabay, 435p.)
J.-P. Vernant, 1996. Géométrie et astronomie sphérique dans la première cosmologie grecque, inMythe et pensée chez les Grecs. Études de psychologie historique, réédition, Paris, La Découverte/Poche, 202-215
A. Citations
Aristote, Traité du Ciel, Forme et grandeur de la Terre, II, 14, 297b – 298a [réf1 , p.293-295]
« De plus, il y a aussi les phénomènes saisis par la perception. En effet, si la Terre n'était pas sphérique, les éclipses de Lune n'auraient pas ces sortes de sections : de fait dans les figures qu'elle prend tous les mois la Lune présente toutes les divisions (droite, biconvexe, concave), mais au cours des éclipses la ligne, qui limite la Lune est toujours convexe, de sorte que, puisqu'il y a éclipse du fait de l'interposition de la Terre, c'est la circonférence de la Terre qui, étant sphérique, est cause de cette figure. De plus, de par l'apparence des astres il est non seulement manifeste que la Terre est circulaire, mais aussi que sa grandeur n'est pas énorme. En effet, si nous effectuons un petit déplacement en direction du Sud ou vers la Grande Ourse, le cercle de l'horizon devient de toute évidence différent, de sorte que les astres au-dessus de nos têtes subissent un grand changement, et n'apparaissent plus les mêmes à qui se déplace vers la Grande Ourse ou vers le Sud. En effet, certains astres visibles en Égypte et dans la région de Chypre ne sont pas visibles dans les régions du Nord, et ceux des astres qui sont constamment apparents dans les régions du Nord se couchent dans les régions nommées plus haut. De sorte que non seulement cela montre que la forme de la Terre est circulaire, mais aussi que c'est celle d'une sphère qui n'est pas énorme. S'il n'en était pas ainsi, en effet, les effets d'un déplacement aussi court ne seraient pas évidents aussi rapidement. C'est pourquoi ceux qui supposent que la région des colonnes d'Hercule touche à celle de l'Inde, et que de cette manière il n'y a qu'une seule mer, ne semblent pas faire une supposition trop incroyable. Comme preuve ils invoquent aussi les éléphants dont l'espèce se trouve dans ces deux lieux extrêmes, en considérant que c'est du fait que les extrémités se touchent qu'elles partagent cette caractéristique. Et tous les mathématiciens qui s'efforcent de calculer la circonférence de la Terre parviennent au chiffre de quarante myriades de stades [400 000 stades soit près de 74 000 km]. De toutes ces preuves on tire non seulement que la masse de la Terre est nécessairement sphérique, mais aussi que sa grandeur n'est pas importante comparée à celle des autres astres. »
Ptolémée, Syntaxe mathématique, Le Ciel se meut sphériquement, I, 3 [in Aujac, réf2, p.206]
« Les premières idées sur la question sont probablement venues aux Anciens à la suite d'observations de ce type : ils voyaient le soleil, la lune et tous les astres tourner d'Est en Ouest, en suivant toujours des cercles parallèles ; ces astres, venus d'en bas, se levaient en semblant surgir de terre ; ils montaient alors graduellement jusqu'à un point culminant, puis redescendaient de semblable manière, s'abaissant progressivement jusqu'à finalement disparaître, en ayant l'air de tomber en terre ; après avoir disparu un certain temps, comme prenant un nouveau départ, ils recommençaient à se lever et à se coucher, aux mêmes heures et aux mêmes lieux, pour les levers comme pour les couchers, avec dans l'ensemble une grande régularité et beaucoup de similitude dans le retour des mouvements. Ce qui a conduit les Anciens à l'idée de la sphère, c'est surtout la révolution des étoiles toujours visibles, que l'on voit s'accomplir circulairement autour d'un seul et même centre ; ce point était forcément le pôle de la sphère céleste, car les étoiles proches de ce point tournaient sur de petits cercles, les étoiles plus éloignées décrivaient dans leur révolution des cercles de plus en plus grands, à proportion de la distance, et ce jusqu'à un cercle limite au-delà duquel les étoiles commençaient à disparaître ; parmi ces étoiles qui disparaissaient, on constatait que celles situées plus près des étoiles toujours visibles restaient disparues peu de temps, celles situées plus loin le restaient davantage, à proportion de la distance. Des observations de ce genre ont suffi au début pour donner aux Anciens l'idée de la sphère. »
Ptolémée, Syntaxe mathématique, La Terre ne fait aucun mouvement de translation, I, 7 [in Aujac, réf2, p.219-220]
« D'autres gens aussi avancent des théories qui leur semble plus plausibles. (…) Ils prétendent que rien n'empêche de supposer par exemple que le ciel est immobile et que la Terre tourne autour de son axe d'Ouest en Est, avec une rotation à peu près complète en un jour. (…) Il n'y a qu'une chose qui leur échappe : même si, du point de vue des phénomènes célestes, rien à la rigueur n'empêcherait que, pour plus de simplicité, il en soit ainsi, en revanche, du point de vue de ce qui se passe autour de nous et dans l'atmosphère, une telle opinion serait, à l'évidence, parfaitement ridicule. (…) Il leur faudrait bien reconnaître que la rotation de la Terre serait le plus impétueux de tous les mouvements que l'on constate autour d'elle ; la Terre en effet, en un temps fort bref, accomplirait une révolution si considérable que tous les objets qui ne s'appuieraient pas sur elle paraîtraient se mouvoir toujours dans le même sens, inverse de celui de la Terre ; pas un nuage ne paraîtrait aller vers l'orient, pas un oiseau en vol, pas un projectile n'irait vers l'Est, car la terre les prendrait toujours tous de vitesse, et les précéderait dans son mouvement vers l'orient, si bien que, la Terre excepté, tout le reste semblerait faire marche arrière en direction de l'occident. »
Pour citer cet article :
La structure du Monde - Du cosmos des mythologies au géocentrisme (1/3), Deparis, juin 2017. CultureSciences Physique - ISSN 2554-876X, https://culturesciencesphysique.ens-lyon.fr/ressource/cosmos-geocentrisme.xml