Les composants électriques et leurs analogues en hydraulique - Résistance et condensateur

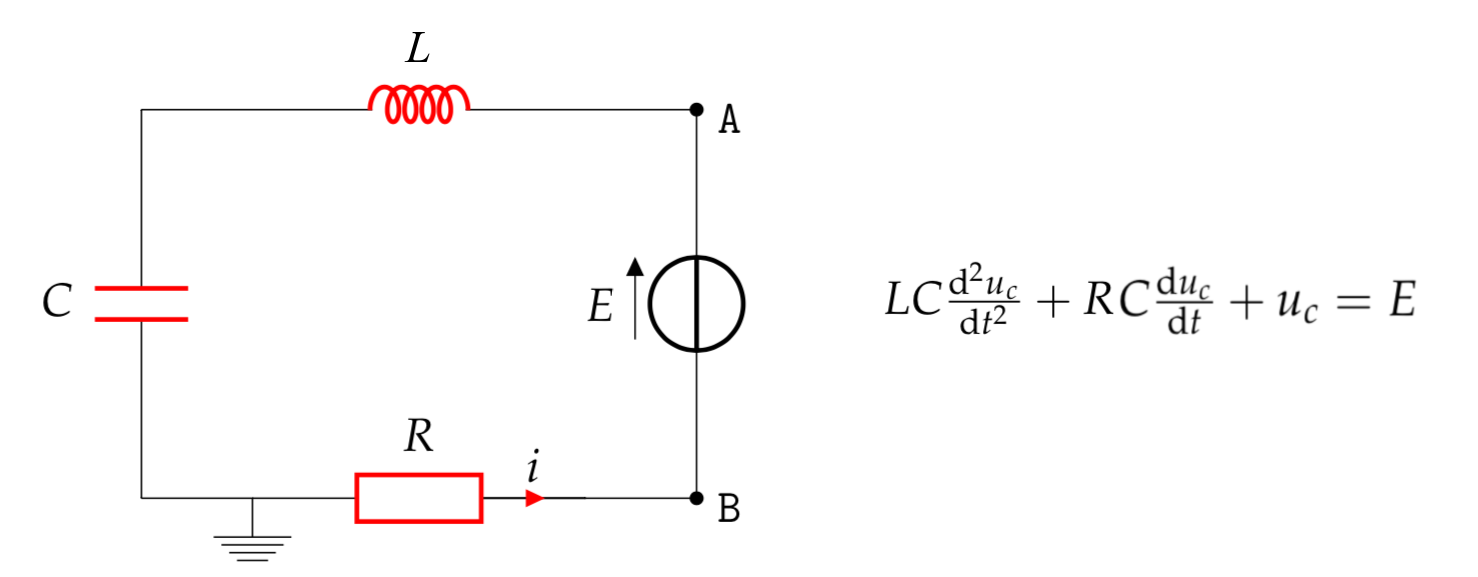
Nous allons nous intéresser à l'étude d'un circuit électrique composé d’une résistance, d'un condensateur et d'une bobine en série.

Figure 1.  Schéma d'un circuit RLC et application de la loi des mailles Remarque : Dans l'équation présenté nous n'avons pas tenu compte de la résistance des fils et des résistances internes de la bobine et du condensateur.

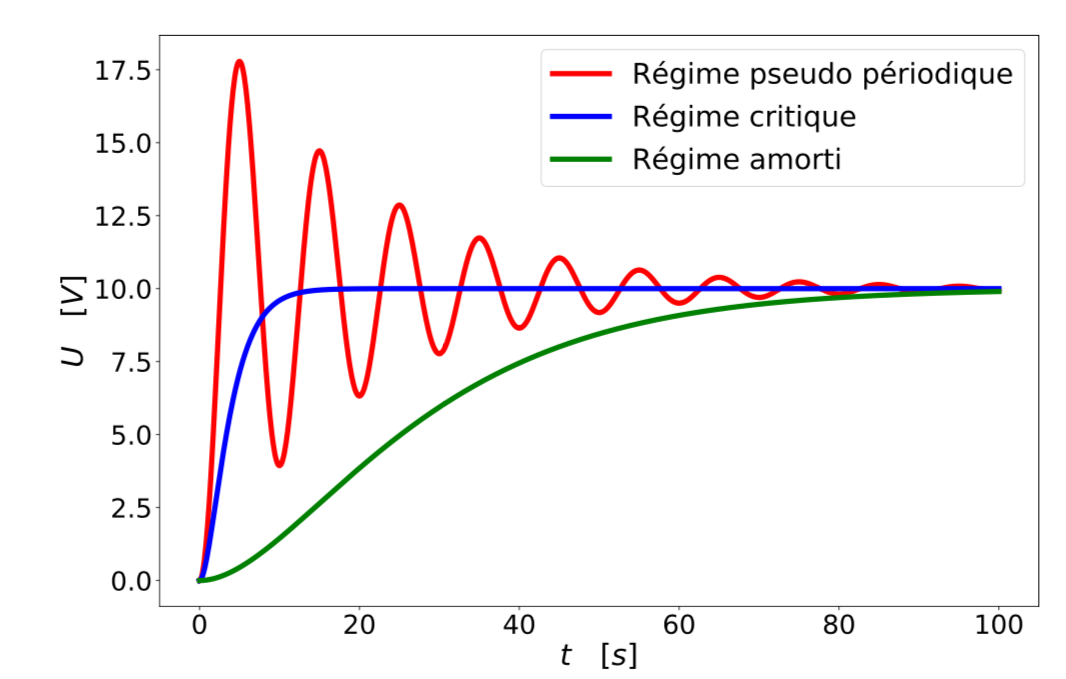
La mise en équation est rapide. La figure 2 représente plusieurs solutions pour l’évolution de la tension aux bornes du condensateur avec des paramètres R, L et C différents pour une réponse à un échelon de tension.

Figure 2.  Différentes réponses de la tension aux bornes du condensateur à un échelon de tension, suivant la valeur des composants du système

Connaissant l’existence d’une analogie entre électrocinétique et hydrodynamique, on peut se demander alors : comment réaliser un tel circuit avec des composants hydrauliques ?

L’analogie hydro-électrique est très répandue et on met souvent en avant la parallèle entre les trois grandeurs suivantes :

Nous allons donc nous baser sur les lois fondamentales de chaque composant pour réaliser un parallèle.

Il convient également de déterminer sous quelles hypothèses l’analogie est valide. On souhaite que l’écoulement dans le circuit soit laminaire, pour éviter les turbulences et effets non linéaires qui rendraient caduques notre parallèle.

On vérifie cette hypothèse en ordre de grandeur :

$R_e=\genfrac{}{}{0.1ex}{}{\rho vr}{\mu }$

Pour de l’eau (viscosité dynamique $\rho$ = 10^-3 kg/(m.s) et masse volumique $\mu$ = 10³ kg/m³) dans un tuyau de diamètre 1 cm (rayon $r$ = 0,5 10^-2 m), en estimant une vitesse $v$ de 0,1 m/s :

$R_e=\genfrac{}{}{0.1ex}{}{10^3\times \mathrm{0,1}}{10^{-3}}\times \genfrac{}{}{0.1ex}{}{10^{-2}}{2}$ = 5.10² < 2.10³

La valeur admise de transition laminaire-turbulent dans un tuyau est d’environ 2 × 10³, l’hypothèse est donc vérifiée.

On souhaite également que le liquide soit incompressible et homogène. Cela est généralement vrai pour de l’eau et nous serons amené à le vérifier par la suite.

Lorsque l’on retranscrit la loi d’Ohm avec les grandeurs hydrauliques, on obtient la relation entre la différence de pression et le débit :

$\Delta P=R\times D$

On cherche donc un composant qui respecterait cette loi, c’est-à-dire qui amènerait une perte de charge.

Plusieurs choix sont possibles, on peut par exemple utiliser des capillaires et utiliser la réduction de section. Cependant, nous avons choisi de tirer profit de la loi de Darcy.

La Loi de Darcy permet de relier un débit à un gradient de pression appliqué au fluide grâce à un paramètre caractéristique du milieu traversé : la perméabilité k .

Figure 3.  Schéma en coupe et photo d’une résistance hydraulique, réalisée en tirant profit de la loi de Darcy (écoulement dans les milieux poreux)

La loi de Darcy donne la relation entre le débit volumique et la différence de pression  : $\colorbox[rgb]{1,1,0}{$D_v=\genfrac{}{}{0.1ex}{}{k\rho g}{\mu }\times S\times \genfrac{}{}{0.1ex}{}{\Delta h}{L}=\genfrac{}{}{0.1ex}{}{Sk}{\mu L}\Delta P$}$         (1)

Avec :

On trouve alors une résistance hydraulique équivalente à :

$R=\genfrac{}{}{0.1ex}{}{L\mu }{Sk}$

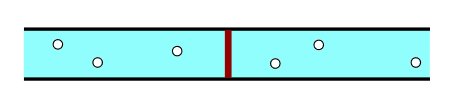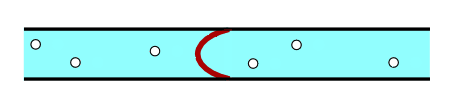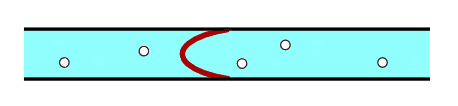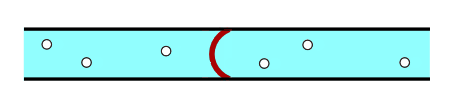
Nous avons réalisé plusieurs résistances en plaçant des billes de différents diamètres dans un morceau de tuyau calibré (12 cm de long), figure 3.

Nous faisons donc varier uniquement le paramètre $k$, la perméabilité.

Pour chaque résistance testée, le morceau de tuyau a la même géométrie et le fluide utilisé est le même : de l'eau. La mousse poreuse a une résistance négligeable et permet simplement aux billes de rester correctement confinées.

On peut estimer rapidement l’ordre de grandeur de la résistance :

$R=\genfrac{}{}{0.1ex}{}{L\mu }{Sk}=\genfrac{}{}{0.1ex}{}{10^{-1}\times 10^{-3}}{10^{-4}\times 10^{-6}}$ = 10⁶ Pa.m^-3.s

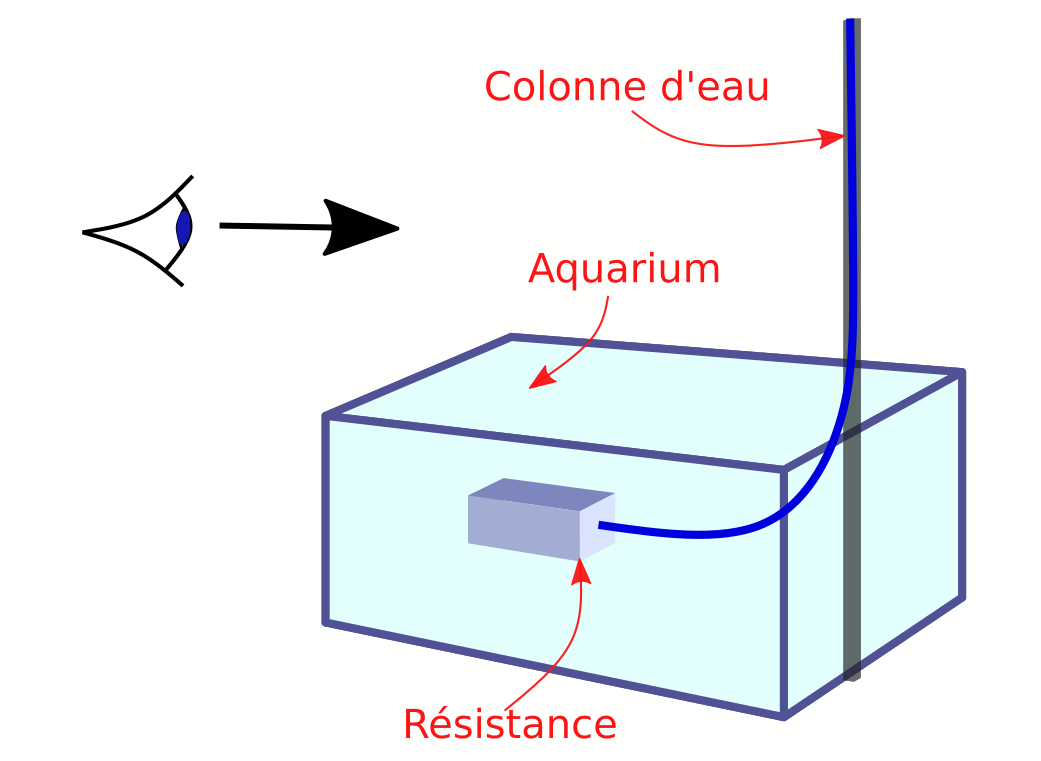
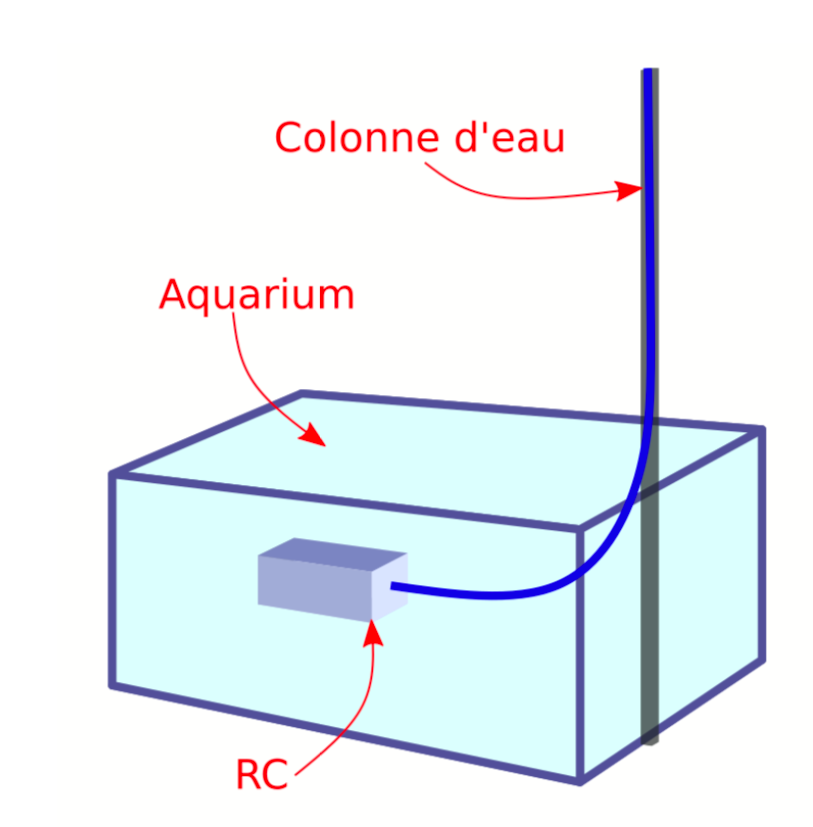
On réalise le montage suivant, permettant d’évaluer la valeur de chacune des résistances réalisées, figure 4.

Figure 4.  Gauche : Schéma du montage de mesure de la valeur d’une résistance hydraulique. Droite : Extrait d'un enregistrement de l'écoulement dans la colonne d'eau

On filme une colonne d’eau qui s’écoule à travers la résistance dans un aquarium (celui-ci est suffisamment grand pour avoir une variation de hauteur négligeable).

On essaie de retrouver la relation :

$\Delta P=R\times D_v$

Le débit volumique s'écrit : $D_v=S\genfrac{}{}{0.1ex}{}{\mathrm{dh(t)}}{\mathrm{dt}}$

La différence de pression s'écrit : $\Delta P=\rho g\mathrm{h(t)}$

Avec : $\mathrm{h(t)}=\genfrac{}{}{0.1ex}{}{1}{\rho S}\genfrac{}{}{0.1ex}{}{\mathrm{dm(t)}}{\mathrm{dt}}$

On trouve l'équation différentielle :

$\genfrac{}{}{0.1ex}{}{\mathrm{dm(t)}}{\mathrm{dt}}=\genfrac{}{}{0.1ex}{}{g}{SR}\mathrm{m(t)}$

Il est également nécessaire d’utiliser l’hypothèse d’incompressibilité, puisque l’on mesure le débit à un point (haut du tuyau) et on suppose qu’il est identique à un autre point (à travers la résistance).

En appliquant la condition finale : m(t) = m_∞, c'est-à-dire l’eau du tuyau est au niveau de celle de l’aquarium lorsque t → ∞), cette équation admet comme solution :

$m\left(t\right)=m_{\infty }(1-\exp (-\genfrac{}{}{0.1ex}{}{g}{SR}t\left)\right)$

Ce qui peut s'écrire :

$\colorbox[rgb]{1,1,0}{$\ln \left(\genfrac{}{}{0.1ex}{}{m_{\infty }-m\left(t\right)}{m_{\infty }}\right)=-\genfrac{}{}{0.1ex}{}{g}{SR}t$}$         (2)

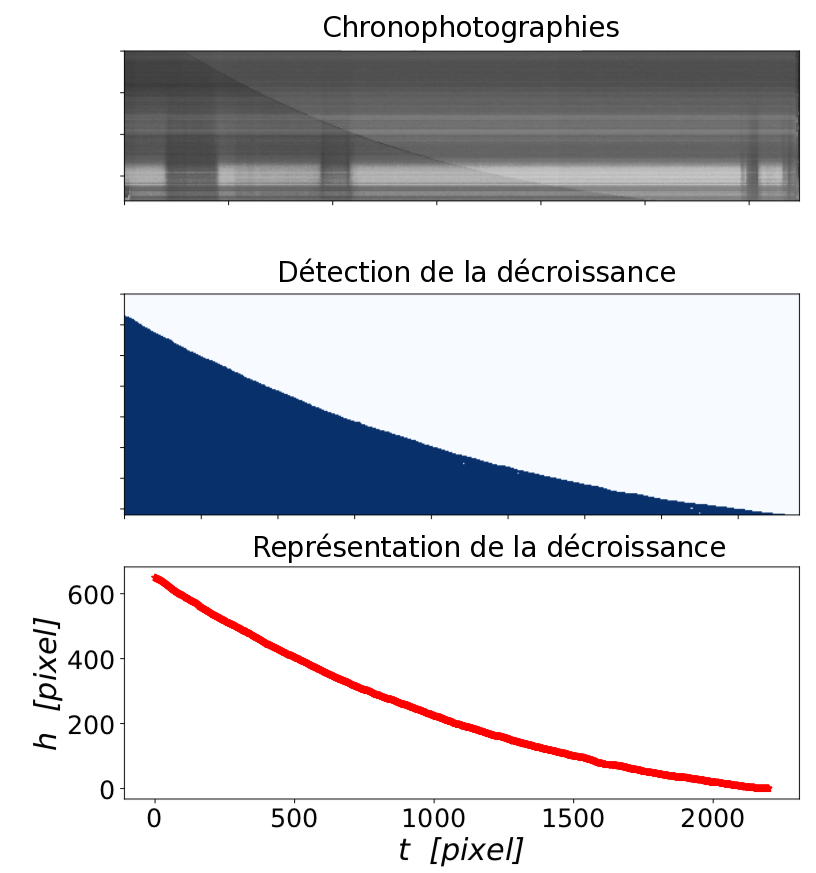
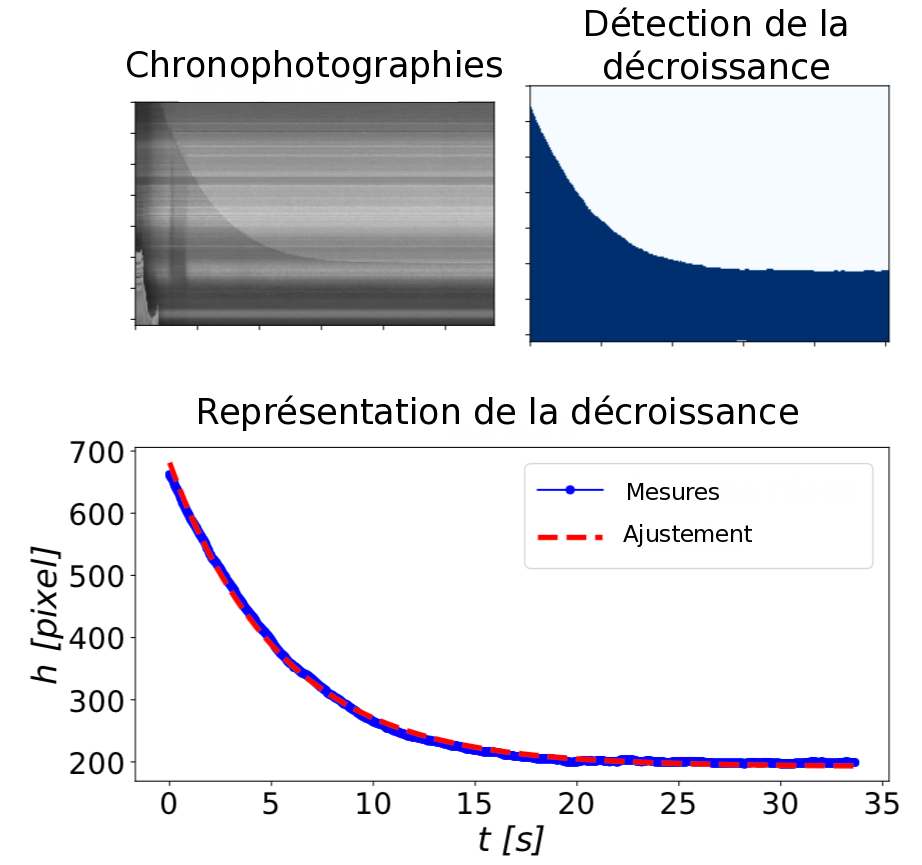
Pour analyser les vidéos obtenues avec les différentes résistances, nous avons réalisé des chronophotographies. Cela signifie que nous avons mis bout à bout une ligne verticale de pixels : chaque ligne correspond donc à une image. Cette représentation permet de visualiser simplement la décroissance du niveau de l’eau en prenant une ligne verticale sur le tuyau, comme on peut le voir sur la figure 5.

Figure 5.  Détermination de la valeur d’une résistance. Les vidéos sont filmées à 30 images par secondes, 30 pixels horizontaux correspondent donc à 1s

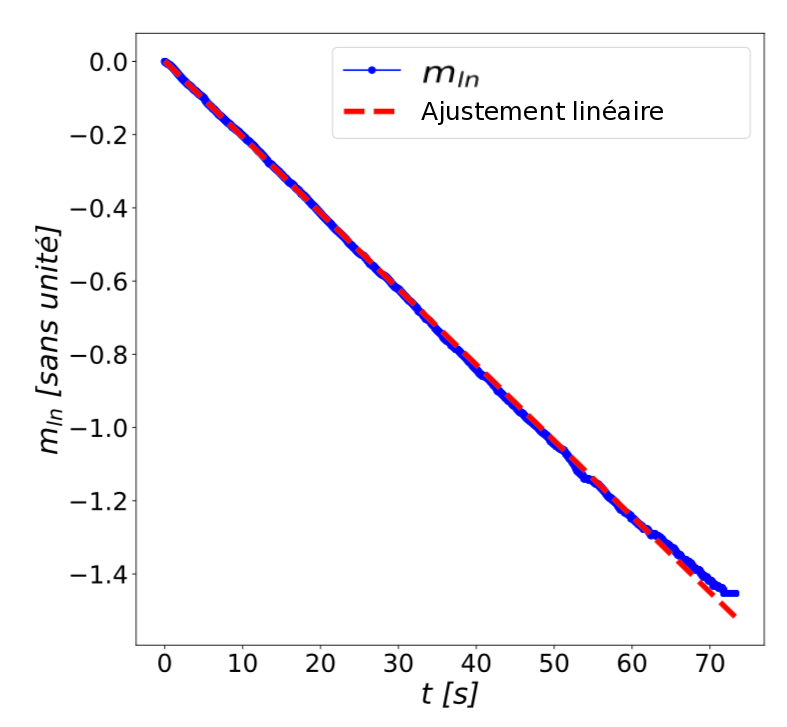
Afin de déterminer la valeur R de chaque résistance nous avons exploité la relation (2) et tracé m_ln =  $\ln \left(\genfrac{}{}{0.1ex}{}{m_{\infty }-m\left(t\right)}{m_{\infty }}\right)$ en fonction du temps. Nous nous attendions à obtenir une droite dont la pente était inversement proportionnelle à la résistance. C’est ce que nous avons obtenu, figure 6.

Figure 6.  Détermination d'une valeur de résistance pour une taille donnée de billes. Les résultats expérimentaux sont tracés en bleu, la modélisation est tracée en rouge

Figure 7.  Valeur des résistances en fonction du diamètre des billes utilisées

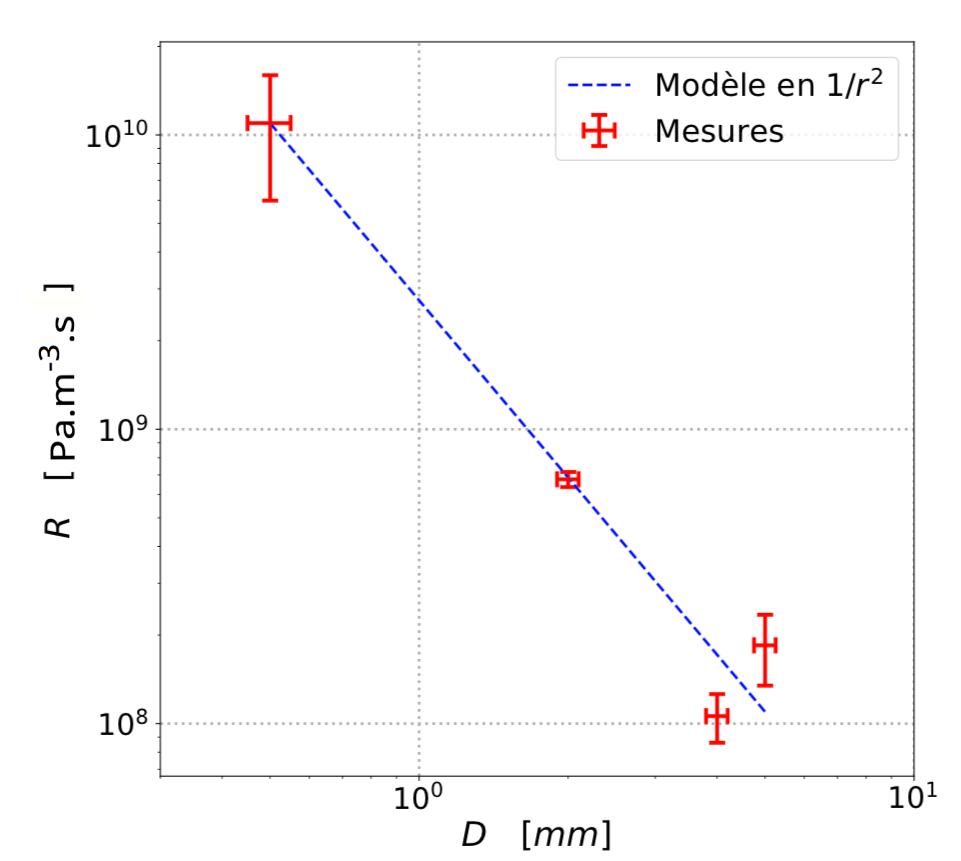
D’après la loi de Darcy, relation (1), nous nous attendions à avoir une dépendance de R en l’inverse du carré du diamètre des billes (soit la surface S d’un cercle de la taille de la bille). Cette relation se confirme, figure 7, où les mesures de la résistance tracées en échelle logarithmique mettent en évidence une droite de pente −2.

Nous avons donc réussi à :

Nous nous intéressons maintenant à une capacité. Dans un premier temps, on essaie de retrouver la relation fondamentale :

Q = C × U soit ∆V = C × ∆P

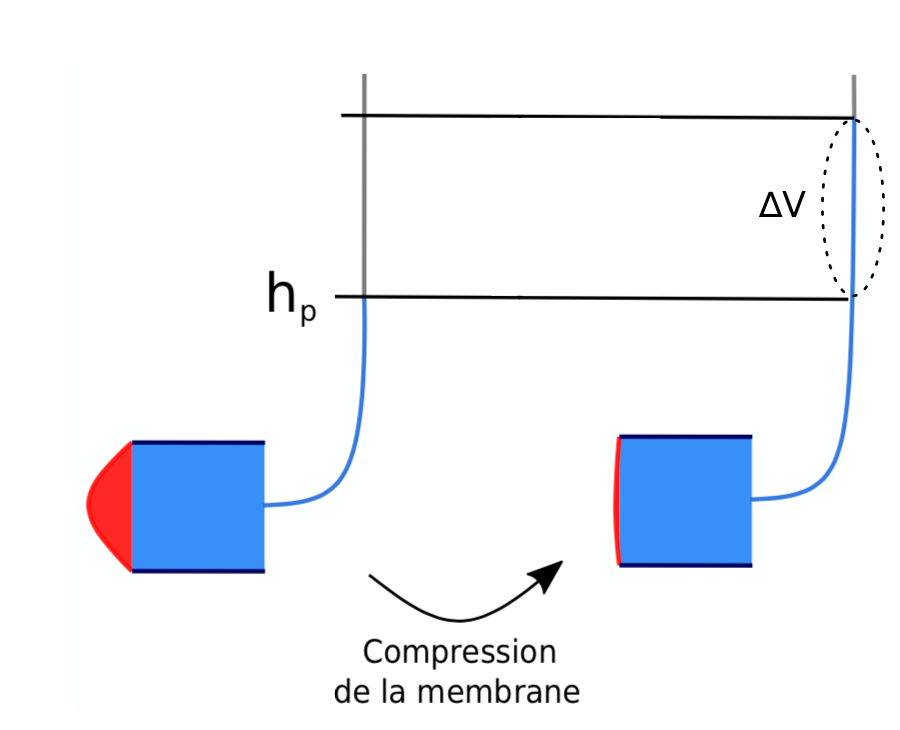
Pour cela, on choisit de placer une membrane élastique sur un morceau de tube, figures 8 et 9.

A priori, cette configuration reproduit correctement les comportements en hautes (oscillations de la membrane) et basses fréquences (le continu est coupé) d’un condensateur.

Figure 8.  Représentation du bilan des forces exercées sur la membrane

Figure 9.  Photo du condensateur réalisé

3.1 Détermination de la capacité hydraulique réalisée

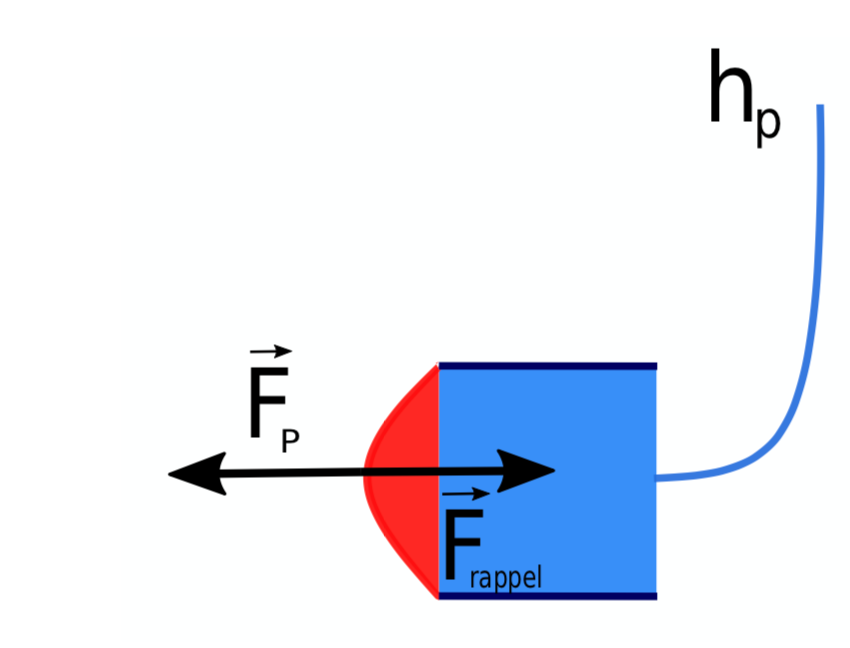
Afin de mesurer la valeur de la capacité créée, nous avons mis en place le protocole suivant, figures 10 et 11 :

Nous avons plongé le condensateur dans l'aquarium rempli d’eau et nous avons mesuré le volume d'eau déplacé ΔV en comprimant la membrane pour différentes valeurs de hauteur d'eau h_p afin de tracer la relation entre ΔV et ΔP.

ΔP = ρgh_p

Figure 10.  Principe de la mesure de la différence de pression

Figure 11.  Photo du montage du principe de la mesure de la différence de pression

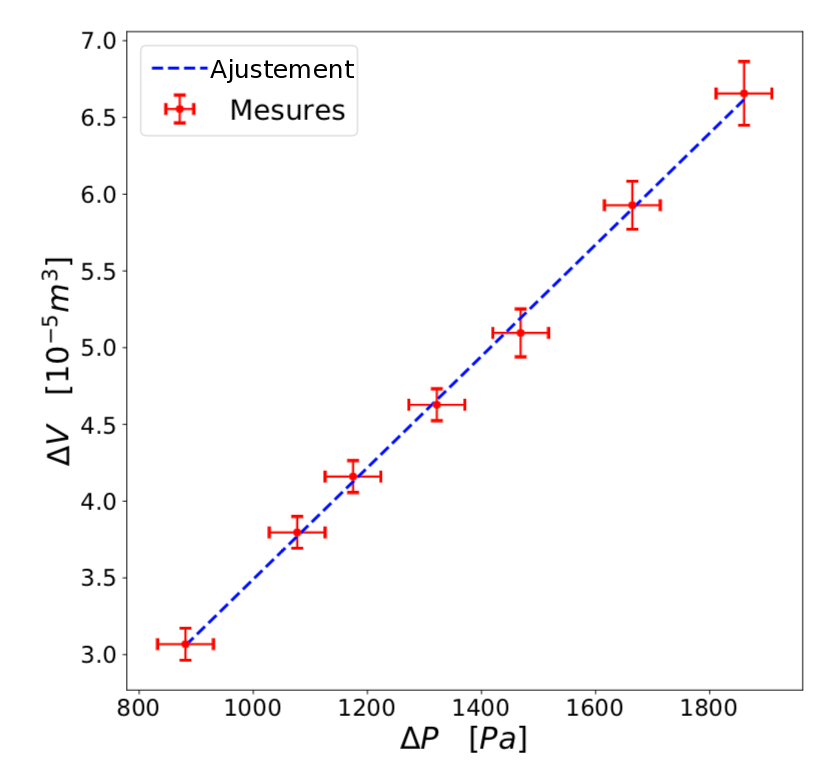
Les mesures mettent en évidence, comme il était attendu, une relation linéaire entre la variation de volume et de pression, figure 12.

Figure 12.  Détermination de la valeur de la capacité hydraulique. Les mesures sont tracées en rouge, l'ajustement des mesures est tracé en bleu, la pente donne accès à la capacité

Les mesures nous donnent alors la valeur suivante pour la capacité réalisée : $C$ = 3,6 ± 0,2.10^-8 m³Pa^-1

Nous avons réussi à créer l’équivalence d’une résistance et d’une capacité en hydrodynamique. Ces composants fonctionnent séparément, mais si on réalise un montage RC série la théorie sera-t-elle toujours vérifiée avec la constante de temps τ = R × C ?

Nous avons placé la résistance et la capacité en série dans l’aquarium, figure 13 et 14.

Figure 13.  Schéma du montage RC série

Figure 14.  Photo du montage RC série

Le protocole est le même que celui utilisé pour l'étude de la résistance. À l’aide d’une caméra, nous avons suivi l’écoulement de l’eau dans la colonne pour accéder à l’allure de l'évolution de la hauteur d’eau en fonction du temps.

Figure 15.  Analyse du circuit RC

On observe, figure 15, une évolution exponentielle de la hauteur d'eau avec un temps caractéristique :

τ = 5,46 ± 0,3 s

Ce temps caractéristique est à comparer avec le temps caractéristique τ = R × C en prenant pour valeurs de résistance et de capacité celles mesurées précédemment.

Le résultat de nos mesures sur C, figure 10, montre que l'on peut être confiant sur la valeur de capacité. Le condensateur choisi pour le cisrcuit RC a une capacité de :

C = 3,6 ^-8 m³Pa^-1

Pour la résistance utilisée, les données s'alignent avec moins de précision, figure 7. En accordant la confiance à l'ajustement, pour des billes de 3 mm de diamètre, on trouve une résistance de :

R = 1,5.10⁸ Pa m^-3s

La valeur théorique du temps caractéristique est alors :

τ = R × C = 5,4 ± 0,5 s

Les deux valeurs théoriques et expérimentales restent assez proches et les barres d’erreurs se recoupent. La théorie marche donc sur nos deux composant résistance et capacité mais aussi pour un montage RC avec ces deux composants.