Expériences historiques contestées, problématiques détournées, anachronismes piégeants (2/3)

Les trois expériences de Galilée, présentées dans cet article et dans les suivants, sont décrites dans les « Discours concernant deux sciences nouvelles », en bref les Discorsi, élaborés en 1633 et publiés en 1638. Ces textes sont une compilation d'écrits de Galilée (1564-1642) remontant, pour l'essentiel, à sa période padouane entre 1592 et 1610, figures 1 et 2.

Figure 1.  Galilée (1564-1642) Source : Portrait au crayon de Galileo Galilei réalisée par Leoni, Wikimedia

Figure 2.  Discours sur deux sciences nouvelles (1638) Traduction de Maurice Clavelin, PUF, Paris, 1995 [1] Source : Wikimedia

Dans la « Troisième journée » des Discorsi, Galilée décrit la célèbre expérience du plan incliné. Il explique que les durées ont été mesurées « avec précision » à l'aide d'une sorte d'horloge à eau.

Après un raisonnement mathématique un peu laborieux (sans la notion de différentielle !) rapporté par Salviati au nom de "l'Auteur" (i.e. Galilée), Simplicio en vient à réclamer une preuve expérimentale. Salviati décrit alors l'expérience menée par "l'Auteur" et dont il affirme avoir été témoin. Clairement, il s'agit de prouver la loi du mouvement accéléré (espace total parcouru "comme" le carré du temps, ou espaces successifs "comme" la suite des nombres impairs).

On peut être étonné de la possibilité d'une mesure suffisamment précise avec un tel dispositif de mesure du temps, mais nous verrons comment cela est possible.

Lors d'une intervention à l'université d'Alger en 2011, le Professeur Ben Daoud, alors doyen, m'a montré les résultats obtenus avec des étudiants de master ayant réalisé une exacte réplique du plan incliné de Galilée, figure 3.

Le groupe d'Alger a répliqué exactement l'expérience selon cette description : longueur de la rampe inclinée, gorge, bille, horloge à eau : au top de départ donné par l'étudiant retenant la boule, le second étudiant retire son doigt qui bloquait l'écoulement de l'eau du bassin, et le remet immédiatement au son du choc d'arrivée (boule contre une plaque métallique). L'eau, écoulée dans un bécher, est alors pesée. La réussite de cette expérience réalisée avec des moyens si simples a beaucoup contribué à me persuader que cette expérience quantitative était, du moins, possible à l'époque de Galilée.

Figure 3.  Réplique du plan incliné de Galilée La longueur du plan incliné est de 5,23 m (i.e. 12 coudées, conformément au texte de Galilée) et le diamètre de la bille (roulant dans un sillon poli) de 18.6 mm. Source de la photo : Pr. ben Daoud et ses étudiants, USTHB, Alger, 2011

La photo de la figure 4 présente l'expérience où toutes les dimensions sont respectées. Au top de départ, l'étudiant de droite libère l'orifice d'écoulement de l'eau du bassin qui est recueillie dans un bécher, puis rebouche rapidement l'orifice au « ding » d'arrivée. L'eau écoulée est alors pesée, exactement comme dans l'expérience originale.

Figure 4.  Réplique de l'expérience du plan incliné de Galilée Source de la photo : Pr. ben Daoud et ses étudiants, USTHB, Alger, 2011

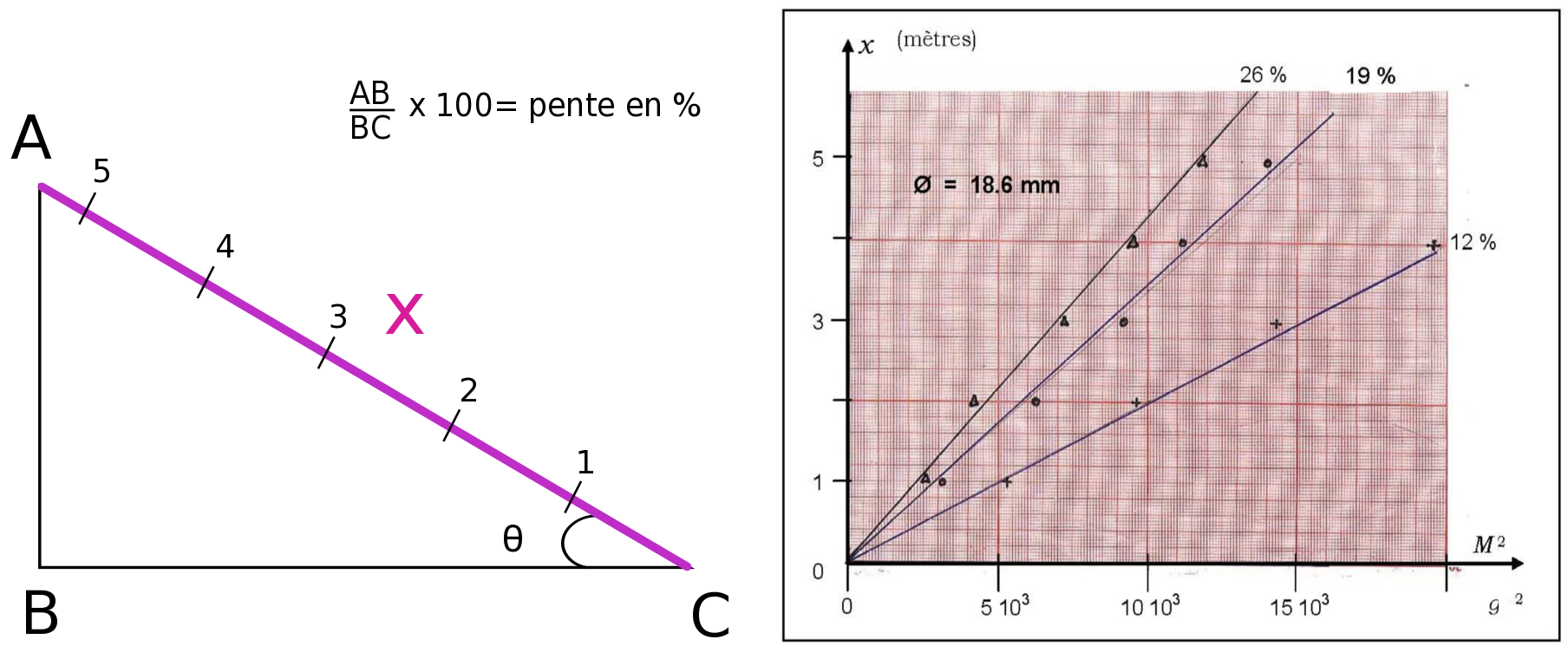
On a représenté sur la figure 5, à droite, la distance x (en mètres) parcourue sur le plan incliné par la bille en fonction du carré de la masse M d'eau écoulée. La figure de gauche présente un schéma du plan incliné, où sont représentés les distances x et le calcul de la pente. Pour chaque inclinaison, les billes sont lâchées successivement à 1, 2, 3, 4 et 5 mètres.

Figure 5.  Schéma et résultats de l'expérience du plan incliné de Galilée Source : Pierre Lauginie, résultats obtenus à l'USTHB-Alger (2011) par Pr M. ben Daoud et ses étudiants

La masse M d'eau écoulée est proportionnelle au temps^[1].

On observe que les résultats sont convaincants : les distances parcourues sont proportionnelles aux carrés des temps, pour différentes pentes.

Galilée n'a donc aucunement exagéré en prétendant l'expérience précise. En tous cas, suffisamment précise en vue du but recherché : établir, ou justifier une loi.

Galilée effectue un raisonnement sur la notion de vitesse à partir de l'idée d'une chute sur plan incliné.

Pierre Souffrin en donne une analyse qui paraît tout à fait vraisemblable [2], figure 6.

Figure 6.  Extrait de Écrits choisis d'Histoire des sciences Source : Pierre Souffrin, 2012, Paris, Les Belles Lettres, p.277 [2]

Galilée affirme que, pour une hauteur de chute donnée AB, les vitesses sur des plans différemment inclinés sont « inversement comme les longueurs totales AC et AD », c'est à dire proportionnelles à la pente (au sinus de l'inclinaison).

Galilée a été sévèrement critiqué par l'historiographie moderne pour cette affirmation : il semble affirmer une proportionnalité entre la vitesse et la pente, alors que ce sont les accélérations qui sont proportionnelles à la pente. Serait-il incohérent avec lui-même, lui qui, dans les Discorsi, affirme que les vitesses à l'arrivée, comme les vitesse moyennes, sont égales ?

On a énormément glosé sur un Galilée dont l'opinion – soi-disant initialement erronée sur cette question – aurait évolué ensuite sur quelques années.

Pierre Souffrin fait remarquer qu'il serait bien plus adéquat de se reporter au contexte de l'époque, le tout début XVII^e siècle pour l'étude du mouvement. La notion moderne de vitesse comme quotient de grandeurs différentes n'existe pas, a fortiori celle de vitesse instantanée.

La notion intuitive de rapidité est rendue, le plus souvent, par la distance parcourue en un temps donné. C'est ce qu'on appelle la conception standard préclassique de la vitesse, dont personne n'a dit (mais que beaucoup ont cru) que c'était limité aux mouvements uniformes ! Avec cette définition – encore en cours dans la 1^re moitié du XVII^e siècle – Galilée a raison !

Prenons l'exemple suivant, tableau 1.

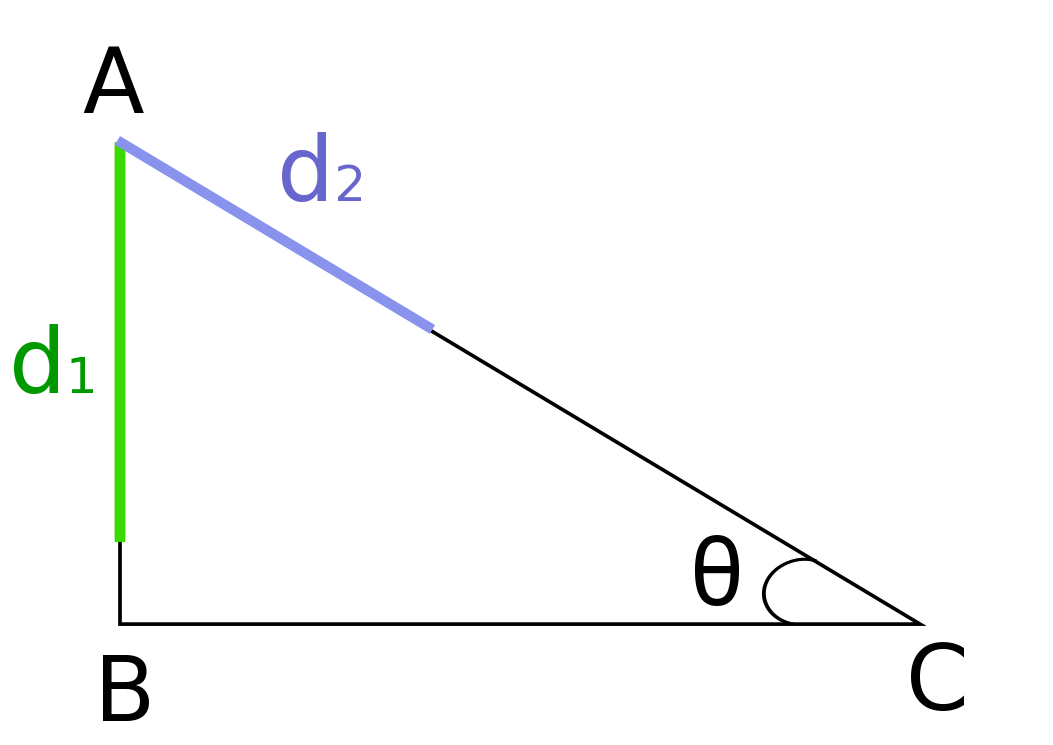
Tableau 1.  Application de la loi des vitesses de Galilée

On cherche la distance parcourue, pendant le même temps, par un même objet, soit chutant de A à B soit sur le plan incliné défini par AC. D'après Galilée, on peut écrire le rapport de proportion entre les deux vitesses : $$ \frac{v_{AC}}{v_{AB}} \propto \frac{AB}{AC} $$ C'est-à-dire :    \( \frac{v_{AC}}{v_{AB}} \propto \sin \theta \) Finalement :   \( v_{AC} \propto v_{AB} \sin \theta \) On fixe ce temps t égal à 1 seconde, et g, l'accélération de la pesanteur, arrondie à 10 m.s-2. À l'aide de la deuxième loi de Newton, selon la direction AB, la distance parcourue par l'objet est d1 = 1/2 gt2 =  5 mètres Selon la direction AC, la distance parcourue par l'objet est d2 = 1/2  (g sin θ) t2 = 5 sin θ mètres

La vitesse standard préclassique est effectivement proportionnelle à l'inclinaison (sin θ), tout comme l'accélération !

N'est-ce pas là une interprétation plus vraisemblable du texte de Galilée, plutôt que de remettre en cause la cohérence de sa pensée ?

Faut-il voir dans cette expérience une tentative de mesure de g ? Non ! Ce n'était pas dans l'air du temps, et de loin.

Une discussion a récemment eu lieu sur une liste de diffusion d'histoire des sciences, où un participant rapportait une question qui lui avait été posée : « Dans l'expérience du plan incliné, Galilée ne donne aucune mesure de g. Ne faut-il pas voir là un argument à l'appui de ceux qui contestent que Galilée ait fait cette expérience ? (sous-entendu : car, évidemment, s'il l'avait faite, il aurait immédiatement donné une mesure de g). »

Rien n'est plus faux. L'idée que l'on fût intéressé, à l'époque, par une valeur numérique de l'accélération est totalement anachronique. Galilée veut établir une loi, celle du mouvement sous une force constante, il s'intéresse à la forme de la loi (en carré des temps), pas à la valeur de l'accélération de la pesanteur g qui est un coefficient de proportionnalité dépendant des unités. On n'écrit pas « = », on dit « varie comme ». De plus, on répugne, et on répugnera encore longtemps, à diviser entre elles des grandeurs différentes, quel sens donner à la division ?

Encore, à la fin du XVIII^e, Cavendish, dans sa célèbre expérience de détermination de la densité moyenne de la Terre, a besoin de l'accélération de la pesanteur pour passer de sa mesure (la force entre deux masses données) à la masse de la Terre [3]. Mais il n'est pas question de g ! L'intensité de la pesanteur est introduite indirectement par la longueur du pendule simple qui aurait la même période d'oscillation que le fléau de sa balance de torsion. Il ne travaille qu'avec des grandeurs fondamentales : des longueurs, des masses et des périodes !

Il y aussi une seconde raison : utilisant le roulement sans glissement d'une boule sur un plan incliné au lieu d'un glissement pur, on montre facilement que l'accélération est alors \( \frac{5}{7} g \sin \theta \) au lieu de \( g \sin \theta \).

La démonstration requiert d'utiliser les concepts d'énergie potentielle, énergie cinétique de translation et énergie cinétique de rotation, moment angulaire et moment d'inertie, toutes notions inexistantes à l'époque de Galilée. L'aurait-il voulu, son expérience ne pouvait conduire, avec les connaissances de l'époque, à une mesure de g. Strictement, vu d'aujourd'hui, avec nos concepts modernes, Galilée n'a pas démontré la loi du mouvement sans frottement sur un plan incliné : il aurait fallu prouver que ce qui était observé avec une boule le serait encore pour un glissement pur, et il n'en avait pas les moyens conceptuels. Mais dire cela, avec nos concepts modernes, ce n'est déjà plus faire de l'histoire, la question, à l'époque, ne se posait évidemment pas.