Activer le mode zen
Ressource au format PDF
Mots-clés
Classification
Statique des fluides - Lois et exemples d'applications
08/06/2020
Résumé
Nous présentons ici les lois de la statique des fluides illustrées par de nombreux exemples.
Table des matières
1. Généralités et propriétés des fluides
1.1 Notions de fluide et d'écoulement
Qu'est-ce qu'un fluide ? Un fluide est un milieu physique, associé aux états liquide ou gazeux de la matière. Un quatrième état de la matière, la plasma, rentre aussi dans la catégorie « fluide » mais ne fera pas l'objet de cet article. Un fluide est caractérisé par sa composition chimique et par ses propriétés physiques : masse volumique, viscosité, tension de surface…
Qu'est-ce qu'un écoulement ? L’écoulement est le mouvement du fluide, caractérisé par un champ de vitesse. Certaines caractéristiques sont liées à l’écoulement et non au fluide. Par exemple, la compressibilité ou l’incompressibilité est une propriété de l’écoulement. La statique des fluides est un domaine de la mécanique des fluides qui s’intéresse aux caractéristiques d’un fluide au repos, sans écoulement.
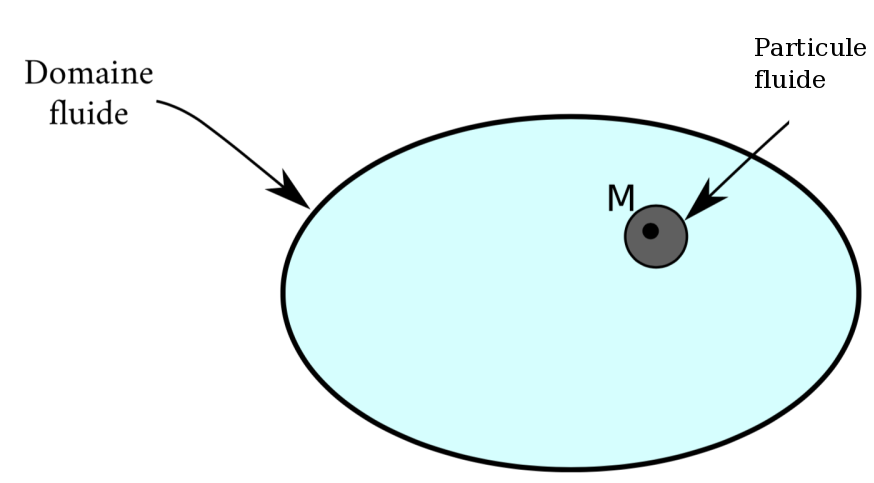
1.2 Particule fluide
Les fluides sont considérés comme des milieux continus : leurs caractéristiques physiques (température, contrainte, vitesse...) varient de façon continue d’un point à un autre du domaine. Ceci implique que les phénomènes que l’on étudie dans le fluide soient à une échelle supérieure à celle des mécanismes que l’on rencontre au niveau moléculaire.
Particule fluide : c’est un volume élémentaire de fluide (échelle mésoscopique ≈ μm3). C’est une échelle d’une part suffisamment petite pour que les grandeurs étudiées (pression, température, masse volumique…) puissent être considérées comme ponctuelles (assimilées au point matériel M) et d’autre part suffisamment grande pour pouvoir considérer le milieu comme continu, c’est-à-dire ne pas avoir à faire une étude discrète de toutes les molécules.
1.3 Grandeurs physiques importantes en statique des fluides
Pression p [Pa]
La pression est une quantité scalaire, fonction de plusieurs variables comme l’altitude. La pression a la dimension d’une force par unité de surface [N/m2]. La pression est isotrope : elle ne dépend pas de la direction.
Les efforts de pression s’exercent :
- au sein d’un fluide
- à une interface entre 2 fluides
- contre une paroi solide
On note patm ou pa la pression atmosphérique. La pression atmosphérique normalisée vaut patm = 1,0125.105 Pa
Masse volumique ρ [kg.m-3]
La masse volumique ρ d'un fluide dépend de la température T et de la pression p. La modification de la masse volumique est due à deux contributions : la dilatabilité (induite par une variation de température) et la compressibilité (induite par une variation de pression).
La masse volumique des liquides est de l'ordre de 103 kg.m-3 alors que celle des gaz est de l'ordre de 1 kg.m-3.
2. Équation fondamentale de la statique des fluides
2.1 Statique des fluides : fluide au repos
La statique des fluides (ou hydrostatique) est l’étude des fluides au repos contrairement à la dynamique des fluides qui s’intéresse à l'étude des fluides en mouvement. On distingue le repos absolu, par rapport au référentiel absolu, du repos relatif, par rapport à un référentiel lié au système qui contient le fluide (c'est-à-dire sans vitesse par rapport à ce système). En statique des fluides, il n’y a pas de mouvement macroscopique d’une particule fluide par rapport à une autre.
2.2 Effort sur une particule fluide au repos
Appliquons la seconde loi de Newton (Principe Fondamental de la Dynamique) à une particule fluide au repos. Cette particule (prenons un cube de fluide pour faciliter la compréhension) subira les forces suivantes :
- une force de volume : son poids
- des forces de surface, c'est-à-dire une force de pression sur chacune de ces 6 faces.
Les forces de pression sur les faces latérales du cube vont se compenser. En effet, il existe un équilibre horizontal du fluide -- Blaise Pascal (1623-1662) : « Dans un liquide en équilibre de masse volumique uniforme, la pression est la même en tout point du liquide et cela aussi longtemps que ces points sont à la même profondeur ».
En statique des fluides (pas de mouvement), la pression p ne dépend que de l’altitude z :
|
p = f (z) |
|
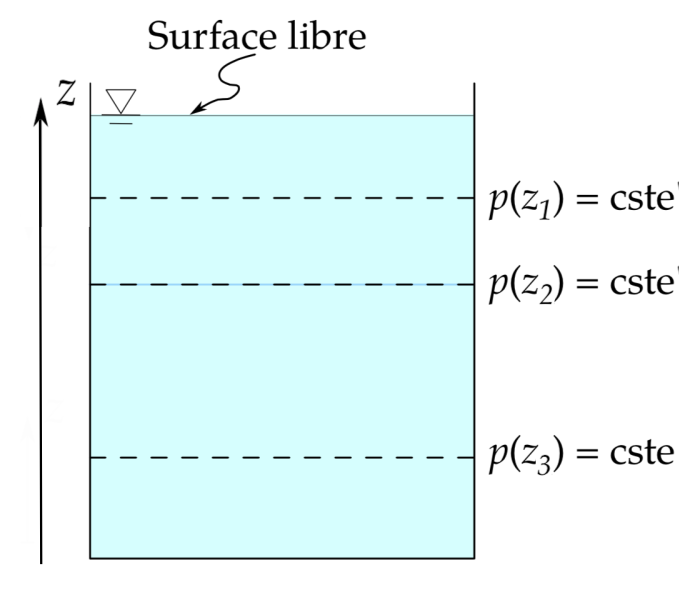
Figure 1. Évolution de la pression dans un liquide |
Le plan d'altitude z est isobare (plan où la pression p reste identique)
La différence des forces de pression agissant sur la face supérieure et inférieure du cube vont s'équilibrer avec le poids du cube. Cet équilibre conduit à l'équation fondamentale de la statique des fluides : dans un fluide, la variation de pression (verticale) entre deux plans horizontaux est égale au poids de la colonne d'eau entre ces deux plans. Par exemple :
p(z2) = p(z1) + ρg(z1 - z2) = p(z3) - ρg(z2 - z3)
Plus généralement, on a :
|
p + ρgz = cte |
On note que le principe d'Archimède (qui d'ailleurs n'a rien d'un principe) est le calul de la résultante des forces de pression s'exerçant sur un corps dans un fluide.
En effet, étudions un volume de fluide au sein de ce même fluide, matérialisé en bleu ciel, figure 2.
Les forces de pression extérieures s'éxerçant sur ce volume sont représentées en violet. Le dessin, à gauche, est en deux dimensions mais les forces latérales s'éxercent de la même manière sur toutes les parois du volume. Ici nous avons choisi un cube mais on peut montrer mathématiquement que les résultats sont rigoureusement les mêmes pour toute autre forme géométrique.
|
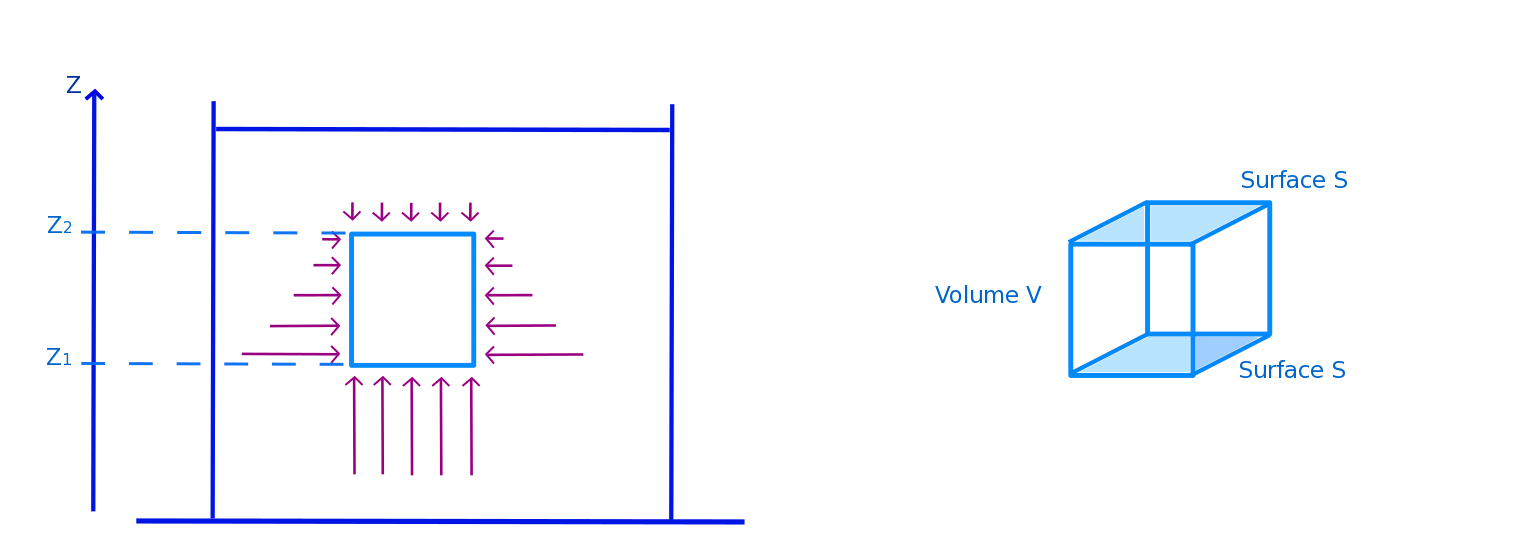
Figure 2. Volume de fluide au sein de ce même fluide On s'intéresse à un volume de fluide au sein de ce même fluide. On matérialise les forces de pression s'éxcerçant dessus. Dans le schéma de gauche n'avons pas représenté la troisième direction, mais les forces latérales s'éxercent de la même manière sur toutes les parois. On appelle S la surface supérieure et inférieure de ce volume V de fluide. |
Nous effectuons un bilan des forces de pression sur ce volume. Les forces latérales de pression étant symétriques, elles s'annulent deux à deux. Il reste les forces de pression s'exerçant sur la face à l'altitude z1 et les forces de pression s'exerçant sur la face à l'altitude z2. Pour ces deux cas, nous calculons les résultantes F1 pour l'altitude 1 et F2 pour l'altitude 2, figure 3.
|
|
|
On appelle S la surface du volume considéré. On projette sur l'axe vertical orienté vers le haut. On a :
F1 = - p(z1).S = - (p0 + ρg(z0 - z1).S)
F2 = p(z2).S = p0 + ρg(z0 - z2).S
D'où la résultante des forces de pression Fa extérieure au volume :
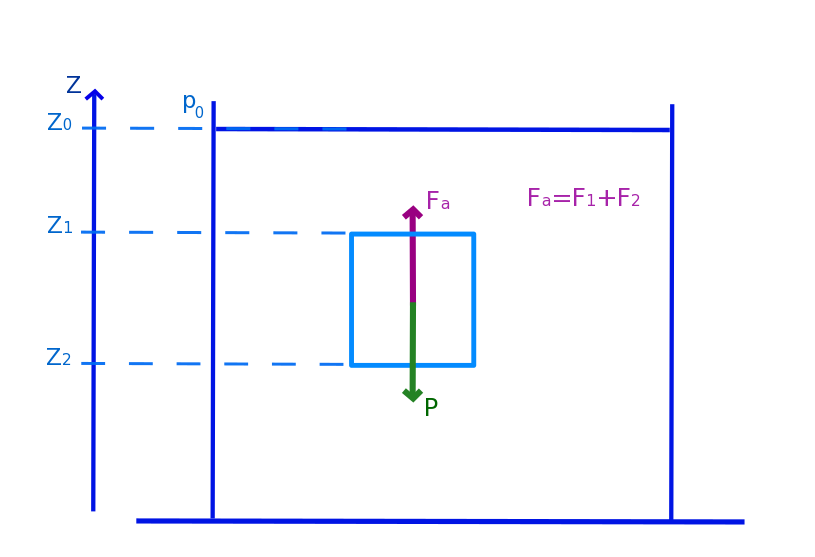
Fa = F1 + F2 = ρg (z1 - z2).S = ρg V
Le volume de fluide étudié est à l'équilibre. La résultante des forces de pression est donc égale au poids du volume d'eau étudié (représenté en vert), figure 4.
On retrouve en effet le postulat d'Archimède :
« Tout corps plongé dans un fluide au repos, entièrement mouillé par celui-ci ou traversant sa surface libre, subit une force verticale, appelée poussée, dirigée de bas en haut et égale au poids du volume de fluide déplacé. »
Au sujet de la poussé d'Archimède, on pourra consulter la vidéo sur « Le principe d'Archimède », présentée par Marc Haelterman, CliPeDia.
3. Exemples d’application de la relation fondamentale de la statique des fluides
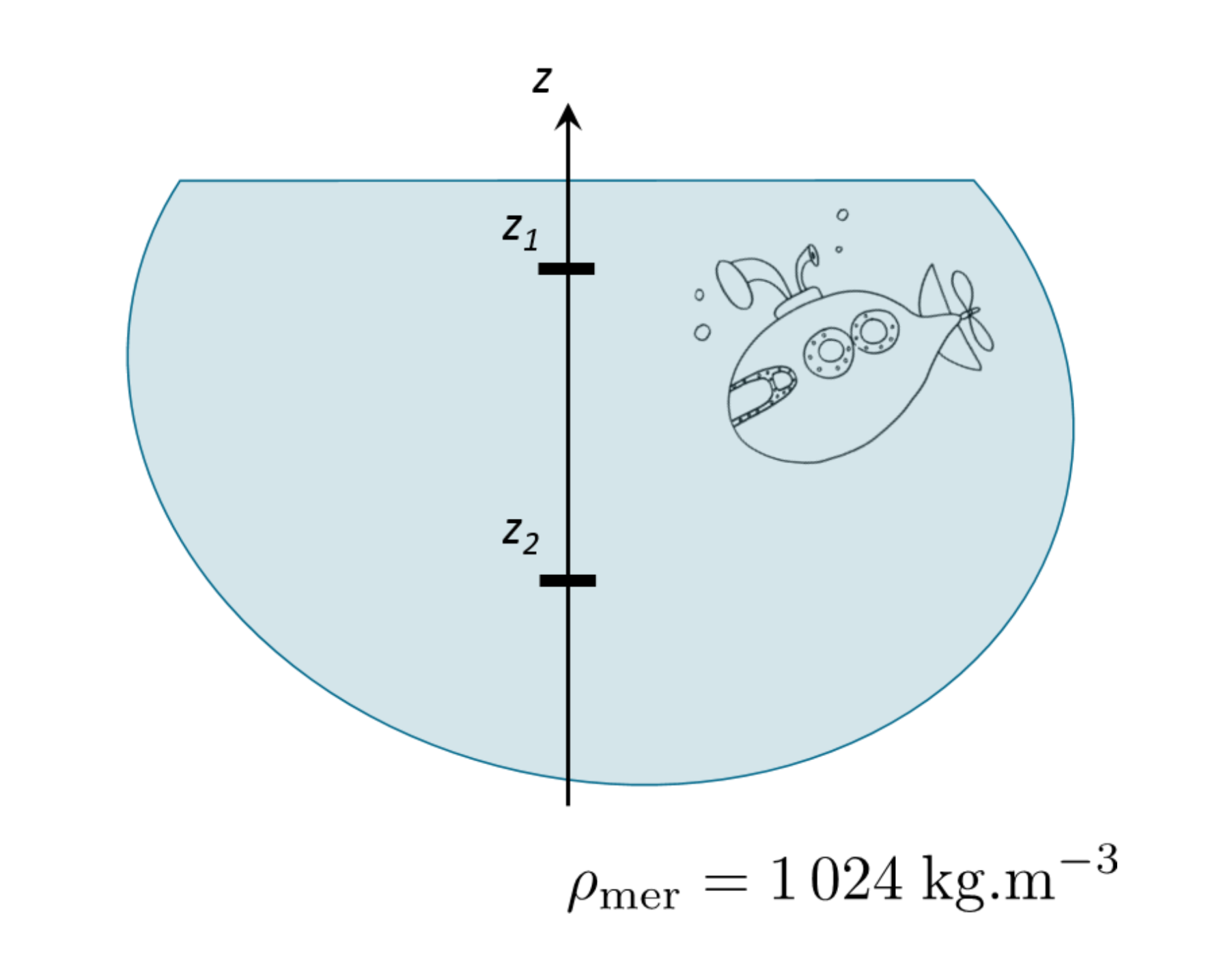
3.1 Exemple 1 : pression subie par un sous-marin
Un sous-marin s’enfonce de 200 m (de z1 à z2 ) dans la mer. Quelle est la variation de pression subie par le sous-marin ?
- 20 bar
- 10 bar
- 0 bar
- -20 bar
Réponse :
On applique l'équation fondamentale de la statique des fluides :
p(z1) +ρgz1= p(z2) +ρgz2
D'où :
∆p = p(z2) -p(z1) = ρg(z1 - z2)
∆p = 1024 x 9,81 x 200 = 2 009 088 Pa ≈ 20 bar
➙ On rappelle 1 bar ≈ 105 Pa
3.2 Exemple 2 : fosse océanique
La fosse des Mariannes, située le long de l’archipel des îles Mariannes dans l’océan Pacifique, est la fosse sous-marine la plus profonde du monde. Sa profondeur est estimée à h = 10 971 m.
À quelle pression doit pouvoir résister un animal marin pour survivre dans cette fosse abyssale si l’on considère la masse volumique de l’eau de mer à 1 028 kg.m-3 ?
Réponse :
À la surface de la mer la pression est égale à la pression atmosphérique :
patm = 1,013.105 Pa
Au fond de la fosse, la pression est de :
p = patm + ρeau de mer gh = patm + p' = 1 107 bar
Soit plus de 1 100 fois la pression que l’on subit sur la terre ferme !
➙ Il est noté que p est appelée « pression absolue ». La valeur de cette pression est donnée par rapport au vide. Elle se distingue de la pression relative p' dont la valeur est donnée par rapport à une référence, habituellement la pression atmosphérique.
On tient tout de même à faire remarquer que les animaux vivant à de telles profondeurs présentent des adaptations à la contrainte de la forte pression hydrostatique. La pression à l'intérieur du corps de ces animaux est la même que la pression externe.
3.3 Exemple 3 : manomètre en U
Un manomètre est un instrument servant à mesurer une pression. La forme en U est une invention de Christian Huyguens. Dans ce type de manomètre, la pression est mesurée par comparaison avec la poussée hydrostatique exercée sur une colonne de fluide.
|
|
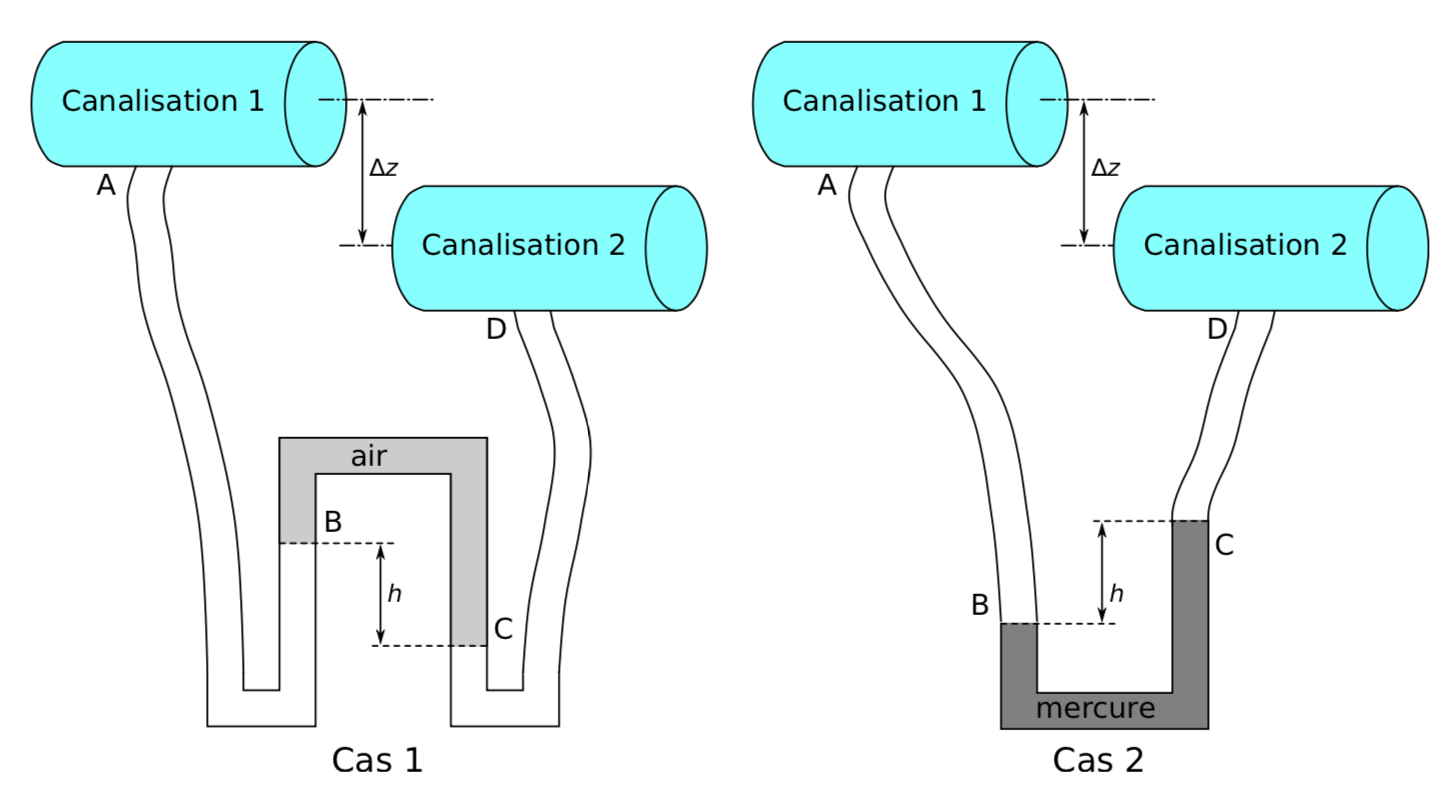
Un tube en U renversé (cas 1) est utilisé pour mesurer la différence de pression entre deux canalisations d’eau (ρeau = 997 kg.m-3). Le tube en U est rempli d’air (ρair = 1,29 kg.m-3).
La différence de pression ∆p entre les deux canalisations fait apparaître dans le tube en U une dénivellation de h = 70 cm.
Déterminer ∆p sachant que la conduite 1 est à une altitude plus haute que la conduite 2 : ∆z = 1 m.
Réponse :
On peut écrire l’équation fondamentale de la statique des fluides entre les surfaces A et B, B et C et C et D, soit :
pA + ρeau gzA = pB + ρeau gzB + ρair gzB = pC + ρair gzC + ρeau gzC = pD + ρeau gzD
En sommant ces trois relation, on remarque que pB et pC vont se simplifier. Il nous reste :
pA - pD = ρeau g (zB + zC - zA - zC) + ρair g (zC - zB)
Or, zB - zC = h, zC - zB = -h et zD - zA = -∆z,
D'où :
∆p = ρeau g (h - ∆z) - ρair g h = -2 943 Pa
La canalisation 1 a une pression plus faible que la canalisation 2.
Comment interpréter le cas 2 où l’air a été remplacé par du mercure (ρmercure = 13 600 kg·.m-3) ?
Cette fois-ci, la pression de la canalisation est bien moins importante ∆p = 0,77 bar.
4. Efforts sur une paroi plane horizontale
Lorsqu'une paroi plane horizontale est immergée dans un liquide, elle subit une force F (poussée hydrostatique) proportionnelle au produit de la pression p(z) à cette profondeur (plan isobare) par la surface S de la paroi :
|
F = p(z) S |
4.1 Exemple 1 : iceberg
Un iceberg de 1 000m3 (10 m x 10 m x 10 m) est immergé partiellement dans de l'eau de mer.
Quelle est la partie immergée h ?
|
Figure 7. Quelle est la partie immergée h ? |
Réponse :
Le poids de l'iceberg Ppoids est équilibré par la force de pression Fpression s'exerçant sur la face inférieure de l’iceberg. Les forces de pression latérales se compensent. Il en vient :
Ppoids = Fpression
D'où :
miceberg g = pS
ρiceberg gV = pS
ρiceberg gV = ρeau ghS
ρiceberg gV / (ρeau gS) = h
h = 8,9 m
Là encore, nous venons de retrouver par le calcul la résultante des forces de pression s'éxerçant sur l'iceberg, correspondant à la poussée d'Archimède.
La poussée d'Archimède s'éxerçant sur l'iceberg (de côté a, de surface S et de volume V) est de :
L'iceberg est à l'équilibre donc la poussé d'Archimède est égale au poids de l'iceberg.
D'où :
On a alors:
8,9 m
Comme ρiceberg est plus petit que ρeau, l'iceberg flotte et n'est donc pas totalement immergé.
Le poids total de l'iceberg correspond au poids du volume d'eau déplacé (ρeaughS) correspondant.
4.2 Exemple 2 : la presse hydraulique
|
Figure 8. Le fermier peut-il soulever sa vache ? |
Le fermier peut-il soulever sa vache ?
- non
- oui
- je ne sais pas
- oui, la vache et même le troupeau !
Réponse :
On suppose que la variation d’altitude entre les deux pistons est négligeable. Le poids développé par le fermier sur le piston est égal à mg.
À l’équilibre, cette force est équilibrée par la force pression hydrostatique ffermier de l’huile sur le piston du fermier :
ffermier = ps = p (π d 2/4)
Où p est la pression dans le liquide et s la surface (disque) du piston.
Du côté de la vache on en déduit quelque chose de similaire. Cette fois-ci la force de pression hydrostatique Fvache de l’huile sur l'autre piston s’écrit :
Fvache = PS = P (π D 2/4)
Or pour une même altitude, on a p = P.
On en déduit alors que :
4 ffermier /(π d 2) = 4 Fvache /(π D 2)
Soit :
Fvache = ffermier (D / d) 2
ou encore :
Mvache = mfermier (D / d) 2
En réalisant l'application numérique, on trouve : mfermier (D / d) 2 = mfermier x 64 = 5 110 kg
Conclusion la masse du fermier permet de soulever 64 fois sa masse : réponse « oui, la vache et même le troupeau ! » (bon... un troupeau de 10 vaches.)
Article suivant : Utiliser les lois de la statique expérimentalement : Statique des fluides - Application pratique à l'aide d'une carte Arduino programmée en Python
Pour citer cet article :
Statique des fluides - Lois et exemples d'applications, Cyril Mauger, juin 2020. CultureSciences Physique - ISSN 2554-876X, https://culturesciencesphysique.ens-lyon.fr/ressource/statique-fluides.xml