Activer le mode zen
Ressource au format PDF
Mots-clés
Classification
Incertitudes de mesure
27/05/2019
Résumé
Pourquoi faut-il calculer les incertitudes de mesure ? Cet exercice est un incontournable des travaux pratiques de physique dont la nécessité est souvent mystérieuse pour les élèves et les étudiants. « Parce qu’elles existent toujours » est une réponse fréquente à la question « Pourquoi faut-il calculer les incertitudes de mesure ? ». Mais ce n’est pas parce que quelque chose existe qu’il faut absolument le connaître !
Dans ce premier article, nous rappellerons ce que sont les incertitudes de mesure, les causes de leur existence, et nous montrerons que leur estimation est nécessaire lorsque l’on souhaite comparer deux valeurs de grandeurs physiques.
Table des matières
1. L’origine physique des incertitudes
1.1 Il n’y a pas de mesure parfaite
Prenons une mesure très simple, la mesure d’une masse avec une balance à plateau. Une telle balance bascule dès que la différence de masse entre ses deux plateaux est supérieure à un certain seuil. Il est donc possible de comparer trois masses A, B et C telles que la balance montre que A = B, B = C et A > C.
C’est cette expérience, que l’on peut reproduire avec toutes les mesures par comparaison (mesures directes) qui fait dire à Poincaré que contrairement aux mathématiques, il n’y a pas de relation d’ordre dans le continuum des valeurs des grandeurs physiques. C’est ce qu’il explique dans l’introduction de son livre « la science et l’hypothèse »[1]. Pour lui, le continuum mathématique (la droite des réels) est une idéalisation du continuum physique.
Toute mesure en physique repose à un moment où un autre sur une comparaison et le résultat d’une mesure sera donc toujours un intervalle. On a pris l'habitude de donner le résultat de la mesure sous la forme :
M = M0 ± ΔM
- M est le résultat de la mesure d'une grandeur,
- M0 est la meilleure estimation de la grandeur que l'on ait avec toutes les informations disponibles,
- ΔM est l'erreur ou l'incertitude (en anglais uncertaincy) estimée sur la valeur de la grandeur.
Deux remarques pour l'utilisation de ces notions en enseignement :
1. On trouve aujourd'hui les deux appellations erreurs de mesure et incertitudes de mesure. Pour un.e expert.e, ces concepts sont différents et renvoient à des façons de penser la mesure différentes. Néanmoins, lorsque l'on débute, ou que l'on s'adresse à un public débutant, il ne me semble pas prioritaire de différencier ces concepts.
En fonction du niveau d’enseignement et de la précision nécessaire, on peut interpréter la mesure de façon de plus en plus précise en disant que le résultat de la mesure :
- Se trouve dans l'intervalle M0 ± ΔM
- Se trouve de manière très probable (95% de chance, par exemple), dans l'intervalle M0 ± ΔM
- Est décrit par une fonction de distribution de probabilité centrée autour de u(M) / 2. On introduit alors l'incertitude type u(M) associée à la fonction distribution de probabilité décrivant le résultat de la mesure.
1.2 Sources d'incertitudes
On distingue en général deux types de mesures : les mesures directes, et les mesures indirectes – qui reposent sur une ou plusieurs mesures directes.
Mesures directes
Dans une mesure directe on compare la grandeur à mesurer à une grandeur de référence de même nature, prise conventionnellement comme unité. Le rapport entre la grandeur mesurée et la grandeur de référence fournit la valeur numérique de cette grandeur en termes de l’unité choisie. Par le passé on mesurait les longueurs en pouces, pieds, coudées, …
Pour identifier les différentes sources d’incertitude dans une mesure directe, reprenons l’exemple de la mesure d’une masse à l’aide d’une balance à plateau. Pour ce faire, on compare la masse inconnue d’un objet, le mesurande dans le vocabulaire de la métrologie, aux masses d’objets de référence. Nous pouvons déjà voir trois sources d’incertitudes dans cette mesure :
- La balance est une vraie balance physique, sa sensibilité n’est donc pas infinie. Il existe donc un seuil de différence de masses en-deça duquel la balance est équilibrée et ne bascule plus.
- Nous ne disposons en général que d’un nombre fini d’objets de référence de masses connues, ce qui oblige souvent à encadrer le résultat de la mesure.
- Nous ne disposons jamais en pratique de l’étalon de référence d’une grandeur donnée pour faire la mesure, mais d’un objet construit à partir de ce dernier. Il y a donc une incertitude sur les valeurs des grandeurs de comparaison. Les objets peuvent s’être émoussés, salis…
Nous pouvons citer un certain nombre de grandeurs physiques qui peuvent être mesurées « directement ». Dans chaque cas nous pouvons identifier : le procédé de la comparaison, et donc ce qui le limite, ainsi que les objets de référence utilisés dans la comparaison.
Grandeur physique | Grandeur physique de référence au laboratoire | Instrument pour réaliser la comparaison | Sensibilité de la comparaison limitée par : | Plus petit échelon de grandeur de référence |
Masse | « Masses » étalon | Balance à plateau | Les frottements sur l'axe | Plus petite masse |
Longueur | Règle graduée | Yeux de l'opérateur | L'épaisseur des graduations et/ou la capacité de séparation de l'œil | Demi-graduation |
Durée | Période d'un pendule oscillant | Opérateur qui démarre et arrête le chronomètre | Temps de réaction de l'opérateur | Résolution du chronomètre |
Tension | Tensions de références (ex : fem des piles chimiques) | Montage AO à comparateur | Seuil de basculement de l'AO | Différence de tension entre les deux tensions de référence les plus proches |
Résistance | Boite à décades de résistances | Pont de Wheatstone et galvanomètre à aiguille | Frottements dans le galvanomètre, parallaxe pour voir que le courant est nul | Plus petite résistance de la boite à décades. |
Toutes ces sources d’incertitudes ne contribuent en général pas à la même hauteur sur l’incertitude de la mesure et l’on peut en général en négliger certaines devant d’autres. Pour toutes ces raisons liées au processus de mesurage, la valeur d’une grandeur physique ne peut jamais être connue avec une précision infinie. Il faut donc voir le résultat de la mesure comme une graduation sur l’axe des réels, mais une graduation avec une certaine épaisseur.
Nous avons pour l’instant considéré le fonctionnement du dispositif de mesure, mais il faut aussi s’intéresser à l’objet physique ou au phénomène que nous mesurons. Celui-ci peut varier sous l’effet :
- De variables externes : la température d’un objet peut varier en fonction de la température de la pièce et de l’éclairement qu’il reçoit ;
- De par son évolution propre : la tension de surface de l’eau ultra pure évolue rapidement par contamination ;
- De par son caractère aléatoire : le temps de demi-vie d’un échantillon de matière radioactive varie d’un échantillon à un autre, il est défini en moyenne ;
- De par sa « largeur naturelle » : du fait de la durée de vie finie des états d’énergie excités d’un système physique, les raies d’émission de lumière ont une certaine largeur naturelle ;
- De la difficulté de définir un objet : le plan dans lequel se forme une image est théorique, expérimentalement on observe une plage de netteté dont il n’est pas possible de définir facilement les limites. Si l’on mesure la largeur d’une table, cette mesure va dépendre de l’endroit où on la fait : les deux bords ne sont jamais exactement parallèles en tous points.
Pour toutes ces raisons, aussi, le résultat d’une mesure ne peut pas avoir une précision infinie. Il n’y a d’ailleurs même pas de sens à parler de valeur vraie d’une grandeur physique.
Mesures indirectes
La mesure directe n’est pas le seul moyen pour estimer la valeur d’une grandeur physique. Cette valeur peut aussi être estimée en utilisant une relation entre grandeurs.
Exemple 1 : Valeur d'une résistance. On peut déduire la valeur d’une résistance d’une mesure de la tension à ses bornes et de l’intensité la traversant. Il faudra alors estimer l’incertitude sur la mesure de la résistance à partir de l’estimation de l’incertitude sur les mesures de la tension et de l’intensité réalisées : R = U / I
L'incertitude sur l'estimation de la valeur de R sera une fonction de l'incertitude sur U et de l'incertitude sur I (propagation des incertitudes, voir prochain article).
Exemple 2 : Mesure d'une tension. Dans la mesure de tension présentée dans le paragraphe sur les mesures directes, l'opérateur compare la tension à mesurer à un nombre fini de tensions de références. En remplaçant les tensions de références à une rampe de tension (par exemple la tension à la sortie d'un montage AO intégrateur), l'opérateur compare la tension à mesurer à toute les tensions balayées par la rampe de tension. En connaissant la pente p de la rampe, l'opérateur convertit la durée au bout de laquelle l'AO bascule en la tension recherchée : V = p x Δt
L'incertitude sur V sera alors une fonction de l'incertitude sur p et de l'incertitude sur Δt (propagation des incertitudes, voir prochain article).
Mesures parfaites ?
La mesure parfaite des mathématiques, celle où l’on connaîtrait le résultat d’une mesure avec un nombre infini de chiffres significatifs est donc conceptuellement impossible. Pourtant lorsque l’on écoute un enseignant ou un chercheur de physique parler, ou que l’on lit une publication scientifique, toutes les valeurs des grandeurs physiques ne sont pas données avec leur incertitude. On parlera en TD d’une résistance de 2 kΩ, on lira au début d’un article de physique des particules que les expériences ont été menées avec un faisceau de 1,5 TeV. L’incertitude sur ces valeurs n’est pas explicitement donnée, soit parce qu’on n'en a pas besoin dans la situation correspondante, soit parce que le nombre de chiffres significatifs utilisés est une information suffisante pour le lecteur. C’est ce dont nous discuterons dans le prochain paragraphe.
2. Des comparaisons en physique
Est-il absolument nécessaire d’estimer les incertitudes ? Pragmatiquement, les mesures sont en général faites pour être utilisées, c’est-à-dire comparées à d’autres valeurs. Dans la vie de tous les jours : Le pH de l’eau des poissons est-il le bon ? La vitesse mesurée est-elle inférieure ou supérieure aux limitations de vitesse ?, comme en physique : la valeur mesurée est-elle cohérente avec la valeur prédite ? La valeur mesurée correspond-elle à la consigne appliquée ?
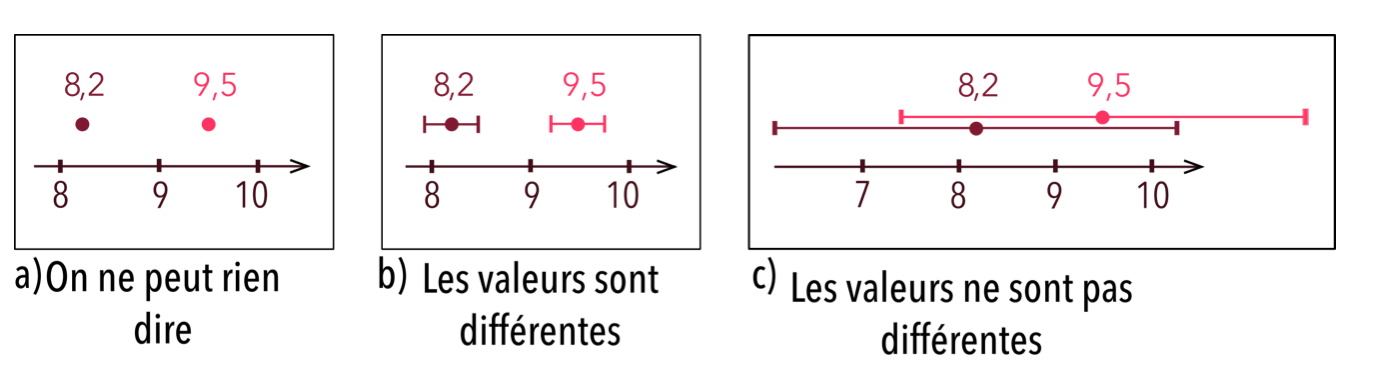
Dans toutes ces situations, il est nécessaire d’avoir une idée de l’incertitude associée aux mesures pour pouvoir les comparer, comme illustré dans la figure 2.
Figure 2. Comparaison de deux mesures |
Si l’on veut que les élèves et les étudiants puissent donner du sens aux incertitudes de mesure, il est conseillé de les confronter à des situations dans lesquelles les mesures réalisées vont vraiment servir. Une analyse des pratiques des physiciens et des physiciennes permet de dégager trois grandes classes de situations qui reposent sur une comparaison en étant plus authentique que la sempiternelle « vérifier une loi » que tout le monde sait juste et pour laquelle l’incertitude est en fait une erreur de mesure.
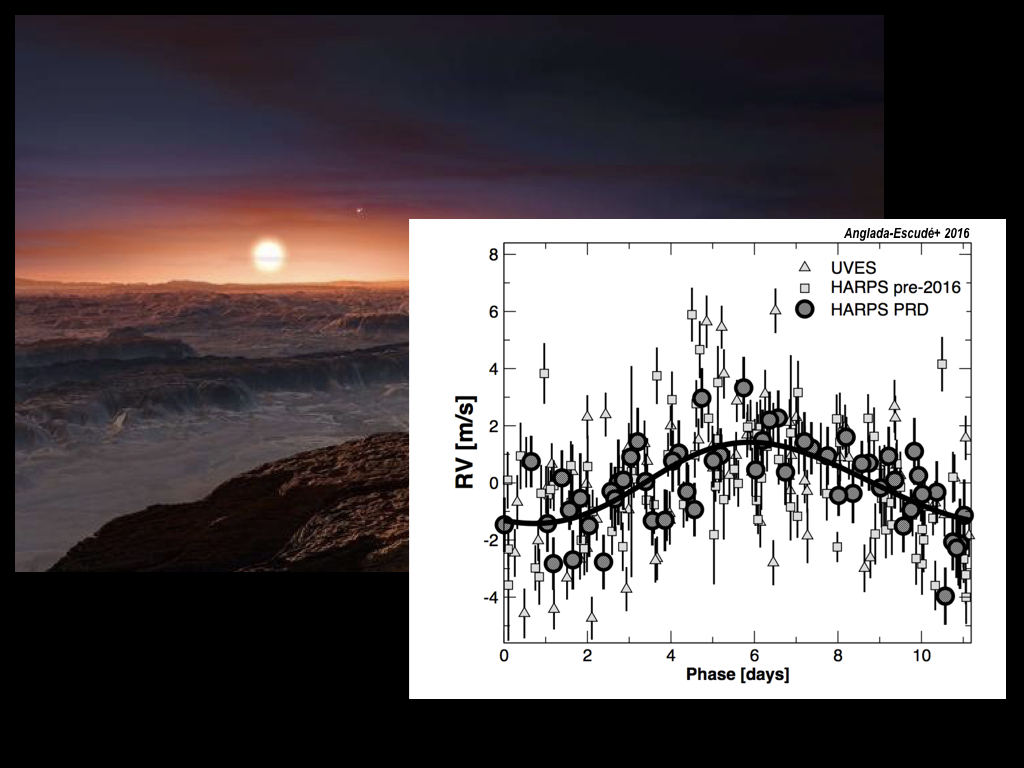
↗ En guise d'illustration, on pourra consulter la conférence de Franck Selsis sur « la détection d'une exoplanète autour de l'étoile Proxima ».
2.1 Modéliser
Il y a aujourd’hui un consensus pour décrire l’activité des scientifiques (et surtout des physicien.ne.s) comme une activité de modélisation : les scientifiques construisent des modèles pour représenter certains aspects du monde pour le comprendre et ou le prédire. Ces modèles sont le fruit de la rencontre entre une théorie et un système physique ou un phénomène. La théorie convoquée nous permet de choisir dans le système physique les éléments que nous allons conserver pour construire un modèle.
Au quotidien, faire de la physique expérimentale, c’est donc construire des modèles et les tester. C’est-à-dire comparer les prédictions du modèle aux mesures réalisées expérimentalement. Lorsque les résultats d’une mesure ne concordent pas avec les prédictions d’un modèle, cela peut signifier :
- que la mesure a été mal faite,
- que l’une (ou plusieurs) des hypothèses de modélisation n’était pas vérifiée (ou que l’un des calculs était faux),
- et parfois, rarement, quand un très grand nombre d’expériences mettent en défaut les prédictions de modèles dérivés d’une théorie, ces expériences négatives demandent un raffinement de la théorie, ou le développement d’une nouvelle théorie.
En pratique, en TP, lorsqu’une mesure diffère d’une prédiction, c’est l’occasion de discuter des hypothèses de modélisation faites, ou des erreurs possibles. Et pour pouvoir mener cette discussion, il faut pouvoir comparer le résultat de la mesure, donnée avec une incertitude, à la prédiction, donnée elle aussi avec une incertitude.
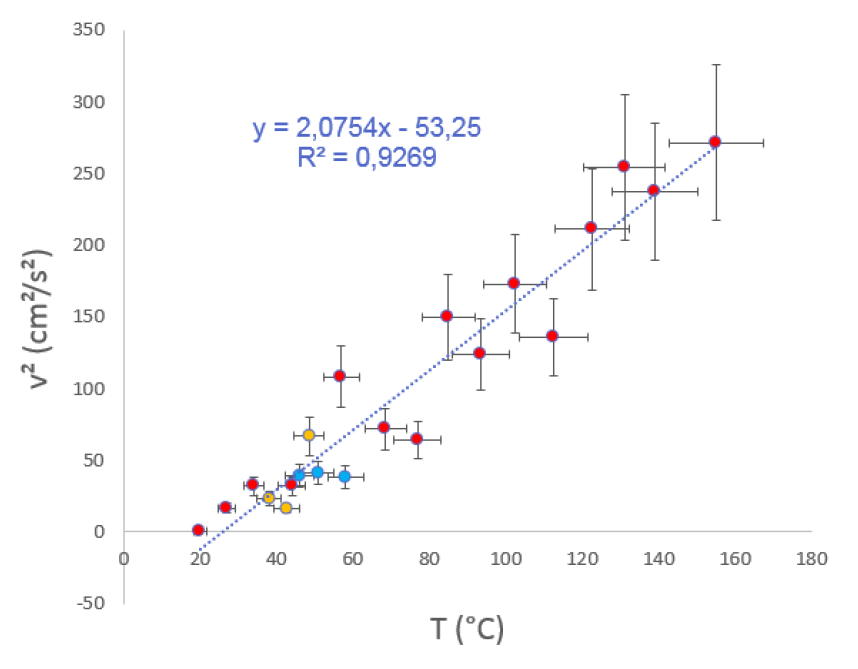
↗ En guise d'illustration de comparaison par rapport à un modèle, on pourra consulter l'article sur « La détermination de la température d'un support » et notamment l'extrait sur La modélisation du phénomène.
Modélisation de la vitesse de montée de volutes v2(T). Les points représentent le carré de la vitesse de montée de volutes au dessus d'un support de température différente de l'air ambiant. Un ajustement affine (en pointillés bleus) donne un bon coefficient de corrélation et une annulation de v2 pour une valeur légèrement supérieure à T0, ce qui confirme notre analyse énergétique prévoyant v2 ∝ (T − T0). En rouge : les points obtenus pour le bloc d'aluminium, en jaune : ceux pour un bloc identique mais en bois, et en bleu : ceux pour un bloc toujours identique mais en PVC. Un ajustement affine des données est représenté en pointillés, avec caractéristiques précisées en bleu. |
2.2 Construire des instruments de mesure
Les scientifiques passent aussi beaucoup de temps à construire de nouveaux instruments de mesure ou à mettre au point de nouvelles méthodes de mesure. Avant de pouvoir utiliser un nouvel instrument ou une nouvelle méthode de mesure, les scientifiques doivent les caractériser. En général, l’une des étapes de cette caractérisation consiste à mesurer un échantillon dont la valeur de la grandeur à mesurer est connue (grâce à une autre mesure faite avec un dispositif de référence). Dans cette perspective il est donc indispensable de comparer à une mesure de référence, et donc d’avoir les incertitudes sur chacune des deux valeurs.
Il est aussi possible d’orienter les expériences de travaux pratiques dans l’esprit de la mise au point d’une méthode de mesure, et de demander aux élèves et aux étudiants de comparer cette méthode de mesure à une autre : précision, répétabilité, coût, temps pour réaliser la mesure, …
Estimer les différentes sources d’incertitude sur une méthode de mesure permet alors aussi d’identifier les modifications à apporter s’il était nécessaire d’améliorer la précision de la mesure réalisée.
↗ En guise d'illustration, on pourra consulter l'extrait de la conférence sur « La détection des ondes gravitationnelles » donnée par Nicolas Leroy.
2.3 Comparer une valeur à une norme, un seuil
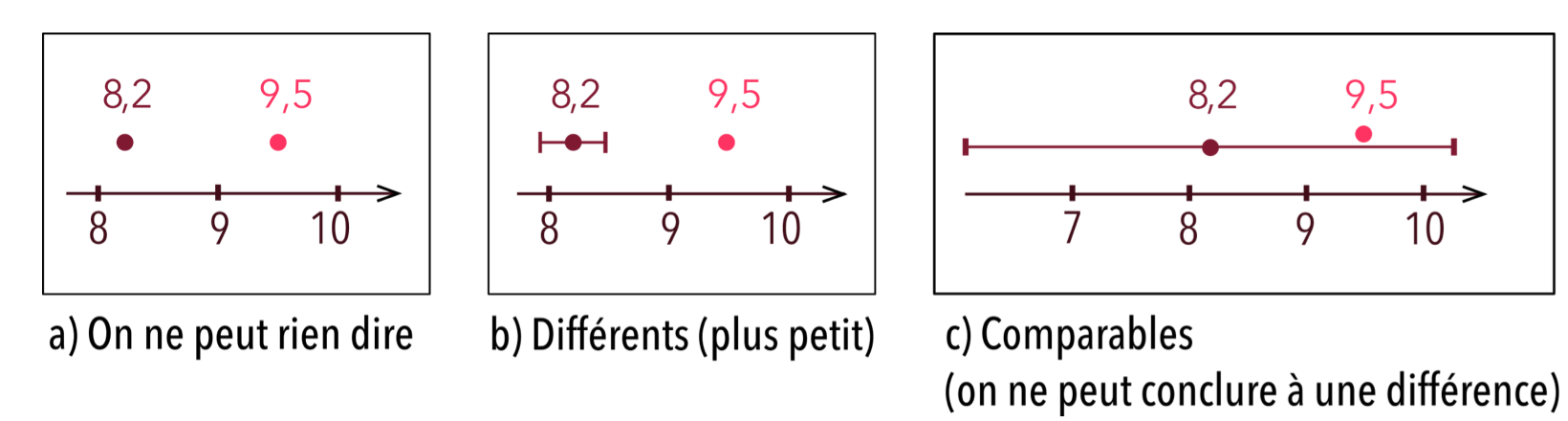
Dans le cadre des activités de recherche, ou bien lors d’analyses (de sang, de sol, d’eau…) ou de contrôle (alcoolémie, vitesse, … ) la grandeur mesurée est comparée à une grandeur de référence : norme ou seuil. Cette valeur est en général donnée sans incertitude et dans ce cas il s’agit de comparer une grandeur intervalle à une grandeur point.
Figure 3. Comparaison de deux mesures |
Parfois, les normes sont assorties de tolérance. Et l’on se ramène au cas où l’on a à comparer deux valeurs intervalles.
↗ En guise d'illustration de comparaison par rapport à une norme, on pourra consulter la conférence de Marc Himbert sur « Le système d'unités de mesure » et notamment l'extrait « Mesurer, c'est quantifier une grandeur et comparer celle-ci à une référence ».
3. Conclusion
En conclusion les calculs d’incertitude sont nécessaires pour permettre la comparaison des valeurs de deux grandeurs physiques. Et réciproquement, lorsque la valeur mesurée ne sera jamais utilisée pour autre chose que pour comparer au résultat de l’enseignant, les calculs d’incertitude poussés n’ont aucun intérêt.
Il y a toute une classe d’expériences d’enseignement conçues pour être démonstratives, et pour que les incertitudes de mesure soient très petites devant l’amplitude des phénomènes à observer. Ces expériences qualitatives servent souvent à aider les étudiants à comprendre « ce qu’il se passe », et c’est très bien ainsi. Et ce n’est absolument pas le moment de faire un calcul d’incertitude car ce n’est pas l’enjeu pédagogique de l’expérience de physique.
D’autres expériences sont au contraire quantitatives. Elles permettent de tester avec précision un modèle (modèle de l’oscillateur harmonique, du pendule pesant), ou de construire un appareil de mesure (un microscope, une lunette astronomique, une balance d’arrachement) qui servira peut être un jour à tester un modèle ou à comparer une valeur à une norme. Dans ces cas, les calculs d’incertitude sont absolument nécessaires. L’enjeu n’est alors pas, en général, d’avoir une estimation au centième de l’incertitude, mais davantage de pouvoir estimer quelle est la source qui contribue majoritairement à l’incertitude, et comment il serait possible de la réduire.
Remarque
Nous avons pour le moment esquissé un raisonnement binaire : les valeurs comparées sont soit différentes, soit comparables. Ce raisonnement est simpliste comparé à celui proposé dans le cadre des théories probabilistes de la mesure pour lesquelles on interprète le résultat des mesures avec des niveaux de confiance. Le résultat de la mesure est alors décrit par une distribution de probabilité que grandeur mesurée prenne une valeur particulière. Cette distribution peut être décrite par son moment d’ordre 1 (moyenne) par un point, et par son moment d’ordre 2 (écart-type) par un intervalle. Cette description n’est donc pas incompatible avec le raisonnement expert actuellement préconisé par l’éducation nationale. Pour autant, ce raffinement me semble contre-productif tant que les autres concepts associés à la mesure ne sont pas bien assimilés.
Au sujet des mesures et incertitudes
Le groupe de travail PEGASE (fruit d'une collaboration entre des chercheurs en didactique et des enseignants de physique-chimie) propose des fiches synthétiques sur les mesures et incertitudes :
Pour citer cet article :
Incertitudes de mesure, Caussarieu, mai 2019. CultureSciences Physique - ISSN 2554-876X, https://culturesciencesphysique.ens-lyon.fr/ressource/incertitudes-mesure.xml