Activer le mode zen
Ressource au format PDF
Mots-clés
Classification
Détermination de la température d'un support par méthode optique (1/2)
19/03/2018
Résumé
≪ Si vous regardez au-dessus d'une surface chaude, l'image apparaît souvent floutée à cause des fluctuations de densité de l'air chaud au-dessus de la surface. Peut-on déterminer la température de la surface en utilisant cet effet ? Quelle est la précision d'une telle mesure ? ≫. C'est ce problème qui a motivé l'étude présentée dans cet article.
Table des matières
1. Introduction
Lorsque l'on est en voiture et qu'il fait très chaud, on peut observer des phénomènes optiques particuliers au niveau du goudron de la route. Si celle-ci est en ligne droite, on peut voir à une certaine distance comme des flaques sur la route, qui disparaissent quand on s'en approche. On peut également s'étonner, par exemple si la route présente une bosse, ou si on distingue bien l'horizon, d'observer comme une couche d'air ≪ flou ≫ au-dessus du goudron. Ces deux phénomènes sont liés aux conditions de température dans lesquelles se trouve l'air au-dessus du goudron lorsque celui-ci est fortement chauffé par l'ensoleillement.
Source - © Nikon support - http://nikonsupport.eu/europe/images/4728/4728.jpg
Une fois ces conditions données, les observations citées s'expliquent très bien dans le cadre simple de l'optique géométrique. On peut toutefois aller plus loin, et essayer d'utiliser ces observations pour remonter à des mesures de température : c'est ce qui a inspiré un des sujets de l'International Physicists Tournament (IPT) 2016, formulé comme suit en français : ≪ Si vous regardez au-dessus d'une surface chaude, l'image apparaît souvent floutée à cause des fluctuations de densité de l'air chaud au-dessus de la surface. Peut-on déterminer la température de la surface en utilisant cet effet ? Quelle est la précision d'une telle mesure ? ≫.
C'est ce problème qui a motivé l'étude présentée dans cet article, orientée vers la mesure de température d'un support.
2. Origine des observations optiques
2.1 Indice optique et température
Pour expliquer simplement les observations présentées, il faut se demander comment des fluctuations locales de température peuvent perturber la marche des rayons lumineux dans l'air. Pour cela, il faut se rappeler que la lumière est faite d'ondes électromagnétiques et l'air de molécules qui sont polarisables sous application d'un champ électrique, donc au passage d'une onde lumineuse.
Cette polarisation vient du fait que noyaux et électrons subissent des forces contraires sous un même champ, leurs charges étant de signe opposé. Les électrons étant bien plus légers, ce sont principalement eux qui sont accélérés par cette force, et sont donc écartés du noyau dans le sens opposé au champ électrique appliqué. Néanmoins, ils restent attirés par le noyau.
L'indice optique d'un milieu dépend en première approximation du nombre de molécules N qui le compose par unité de volume.
Si le milieu est dispersif, il dépend aussi de la longueur d'onde, (figure 1).
Dans cette étude, on négligera le fait que l'indice optique dépend a priori de la molécule atmosphérique considérée : diazote, dioxygène, argon, etc., et l'air sera considéré comme milieu non dispersif sur le spectre visible.
L'indice optique local n de l'air devient une simple fonction croissante de la densité N, de molécules toujours locale, de l'air. Or cette-dernière étant une fonction décroissante de la température T (N étant inversement proportionnel à la température sous l'hypothèse de gaz parfait), on a finalement le constat suivant :
L'indice optique n de l'air décroît avec la température T.
2.2 Mirages et flous
Maintenant que l'on sait que n décroît lorsque T croît, il faut s'intéresser au profil de température de l'air au voisinage du goudron chaud d'une route en été.
Le goudron, solide et foncé, absorbe fortement le rayonnement solaire. Il s'échauffe donc bien plus vite que l'air qui le surplombe. Les deux étant en contact, un mécanisme de transfert de chaleur se met en place : la convection. L'air va donc être chauffé au voisinage du goudron, ce qui va avoir plusieurs conséquences :
- D'une part la montée de volutes d'air chaud, ceux-ci étant moins dense que l'air environnant, et donc entraînés vers le haut par la poussée d'Archimède qui l'emporte sur leur poids ;
- D'autre part, l'établissement d'un gradient vertical de température moyenne au-dessus de la route : au bout d'un certain temps, la convection aura établi un profil de température décroissant entre l'air à altitude nulle et même température T que le goudron et l'air à une hauteur typique h au-dessus de la route et à température atmosphérique T0.
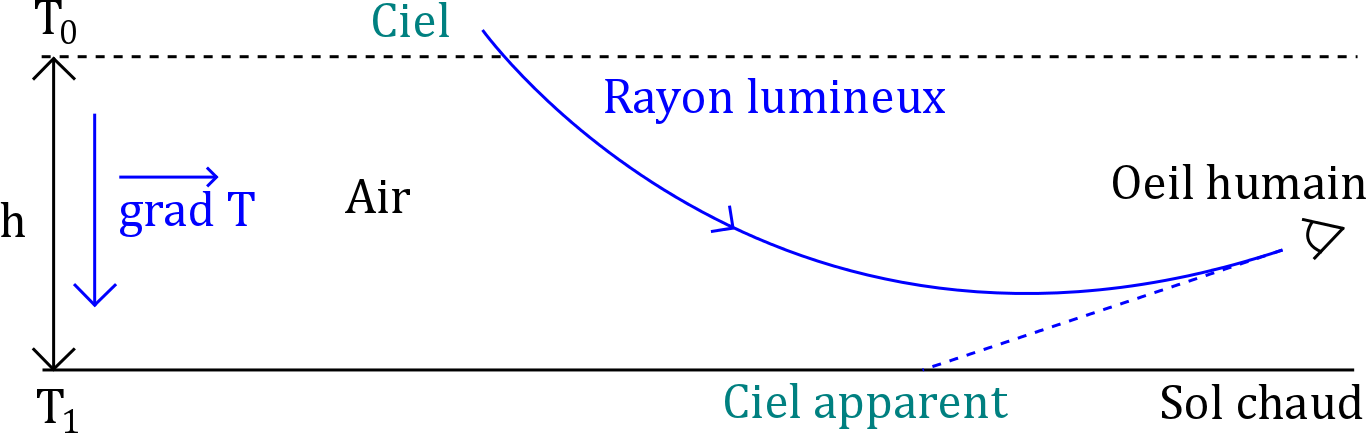
La seconde conséquence est à l'origine du phénomène de mirages, qui s'observe aussi au-dessus du sable du désert. En effet, le gradient vertical de température est à l'origine d'un gradient vertical d'indice optique atmosphérique. Si on modélise celui-ci comme un grand nombre de dioptres plans (figure 2) d'altitude z, qui font passer l'indice de n(z) à n(z + dz) = n(z) + n′(z)dz et que l'on applique la seconde loi de Snell-Descartes, on trouve que les rayons lumineux vont être courbés vers les zones d'indice croissant, donc de température décroissante, ici vers le haut.
C'est ainsi que des rayons venus du ciel, au lieu de poursuivre leur marche vers le sol, se courbent et repartent légèrement ascendants, de sorte qu'ils sont visibles par un automobiliste assez lointain (lorsque l'automobiliste se rapproche, ces rayons deviennent trop bas pour ses yeux). L'œil humain projetant les rayons qu'il reçoit en ligne droite, l'automobiliste voit un morceau de ciel sur la route, comme si une flaque d'eau réfléchissait les rayons venus du ciel : c'est le phénomène dit de ≪ mirage inférieur ≫ (figure 3). Une présentation des mirages supérieurs est donnée en bibliographie [1]
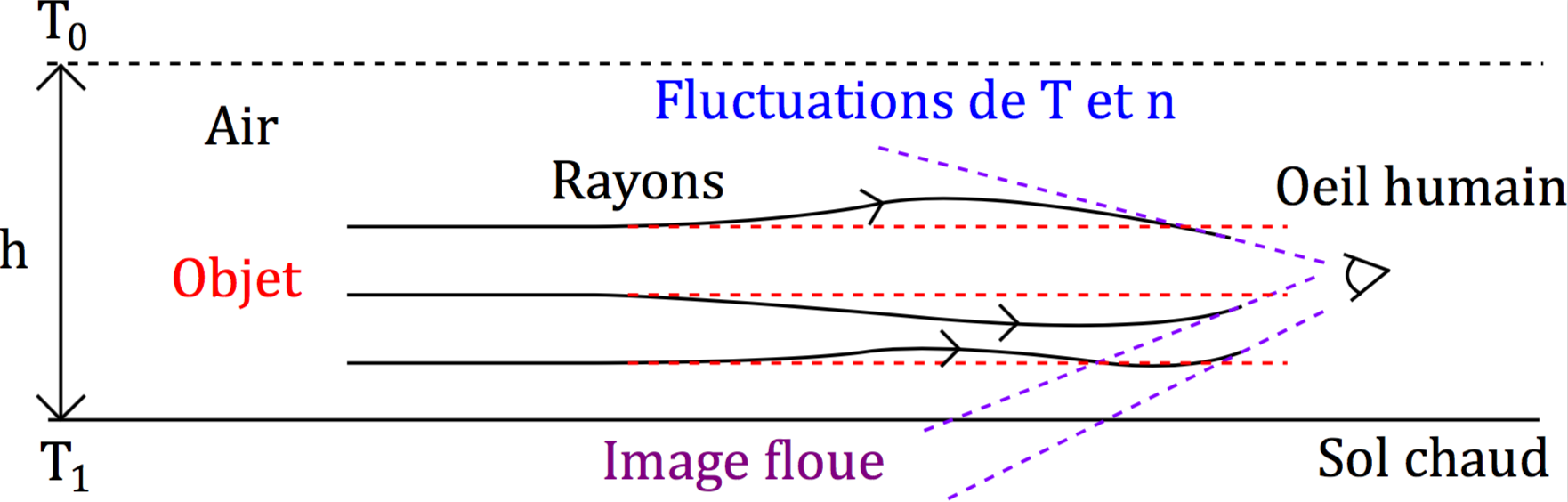
Quant à la première conséquence, c'est-à-dire les volutes d'air chaud, elle se traduit par des zones d'indice optique inférieur, en mouvement ascendant. Par le même principe que celui expliqué ci-dessus, à savoir que les rayons se courbent vers les zones d'indice supérieur, la présence de tels volutes va modifier la marche des rayons rasants, et ce de façon dynamique, puisque les volutes sont en mouvement. Il en résulte, pour l'œil humain, une impression de flou au voisinage de la route (figure 4). Ce flou s'observe d'ailleurs aussi lorsqu'on regarde au loin depuis l'extrémité des quais d'une gare, les rails en acier chauffant également beaucoup l'air qui les surplombe.
De par la formulation du problème donné par l'IPT, c'est l'effet de flou que nous avons choisi d'utiliser pour mesurer la température d'un support donné.
3. Choix d'un dispositif expérimental : Ombroscopie ou objet déformé ?
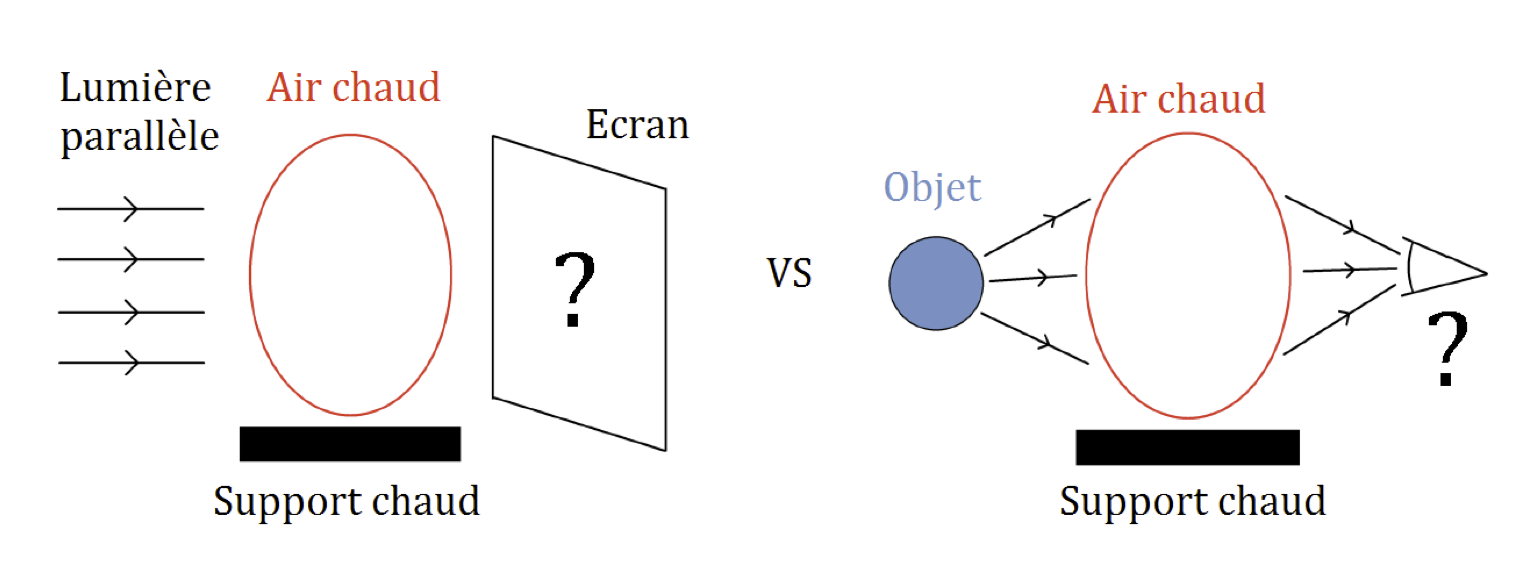
Pour parvenir à remonter à la température d'un support en étudiant les phénomènes optiques dus aux volutes d'air chaud ascendants, il faut une expérience appropriée. Deux principales options s'offrent alors, elles sont présentées dans la figure 5.
Les deux méthodes que nous avons envisagées pour étudier les fluctuations d'indice sont l'ombroscopie et la visualisation d'un objet déformé. On aurait pu envisager aussi la strioscopie, mais elle n'apporte ici pas grand-chose de plus que l'ombroscopie et elle nécessite un montage plus compliqué.
Le principe de l'ombroscopie est le suivant : un faisceau incident parallèle est envoyé sur un milieu d'indice non uniforme (ici, l'air chaud) puis observé sur un écran. Globalement, une déviation est due à un gradient d'indice, mais ici le faisceau est étendu sur une zone où le gradient d'indice n'est pas uniforme. Pour comprendre ce qui se passe, on décompose alors par la pensée le faisceau parallèle en de petits sous-faisceaux parallèles qui vont aborder le milieu en des points différents, donc subir un gradient d'indice différent et ainsi être déviés différemment. L'étude de l'ombre portée sur un écran permet de quantifier ces différences de déviation, donc les variations spatiales du gradient d'indice.
La seconde méthode basée sur l'étude de la déformation d'un objet utilise également la déviation géométrique des rayons lumineux. Maintenant, on se contente de placer un objet lumineux d'un côté de la zone d'air chaud et on l'observe de l'autre côté. À cause des variations d'indice, certains rayons vont se courber et des parties de l'objet n'apparaîtront pas là où elles devraient être : l'objet est déformé. Si on connaît l'allure qu'a l'objet observé à travers de l'air à température uniforme, il suffit d'étudier les modifications de l'apparence de l'objet en présence des volutes d'air chaud pour localiser les volutes en question.
Dans cette méthode, il n'est pas nécessaire de travailler avec de la lumière parallèle. Il suffit d'un objet lumineux et d'une caméra pour l'observer. Par ailleurs, cette technique fonctionne même si l'objet est baigné de lumière naturelle : on ne fait que filmer l'objet au travers de la zone d'air chaud. L'ombroscopie ne présente pas cet avantage : l'étude de l'éclairement de l'ombre projetée nécessite de placer le montage dans une pièce obscure. La seconde méthode est donc non seulement plus simple à mettre en œuvre que l'ombroscopie, mais elle est, en plus, applicable sur une route un jour d'été !
4. Présentation du protocole
4.1 Un damier comme objet déformé
Il reste maintenant à choisir un objet pour parvenir à nos fins, à savoir étudier les fluctuations de l'indice optique au-dessus du support chaud (on entend par là plus chaud que la température de l'air l'ambiant, bien sûr), avec pour but l'utilisation des fluctuations pour mesurer la température du support.
Notre méthode ne nous donne accès qu'à une carte en 2D de ces fluctuations, à moins de posséder plusieurs caméras filmant sous des angles différents, ce que nous avons préféré exclure, mais qui pourrait constituer un prolongement intéressant. Pour profiter au maximum des deux dimensions permises tout en sachant que l'une d'elle (la verticale) dirige le mouvement des volutes d'air chaud, on peut utiliser un damier à carreaux noirs et blancs.
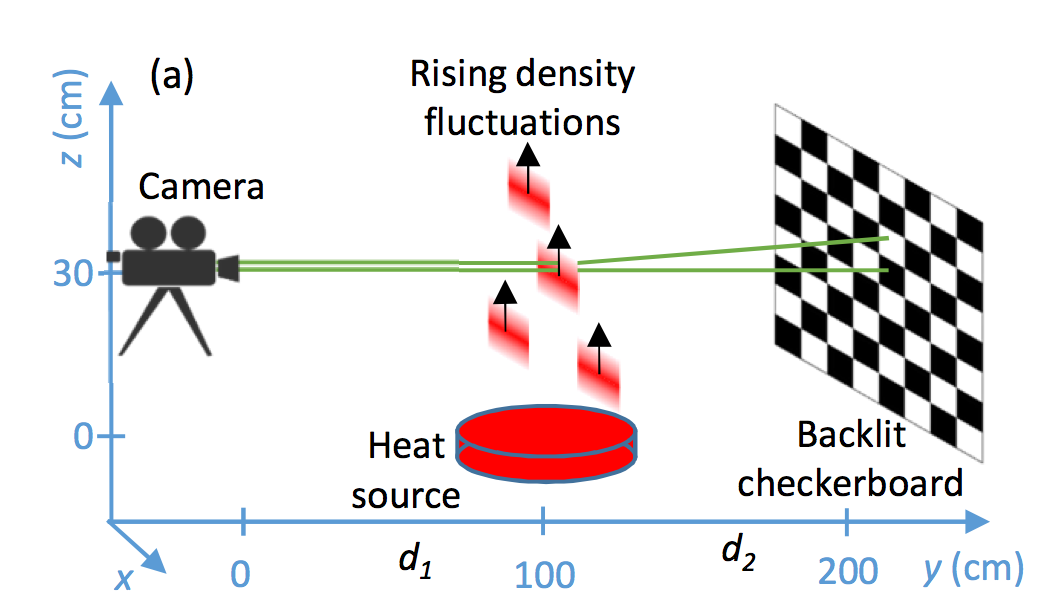
L'idée est simple : on enregistre une image du damier à une distance donnée, avec de l'air à température uniforme T0 (température de la pièce si on travaille en intérieur) puis on dépose un support chaud entre le damier et la caméra et on filme à nouveau.
On va alors observer que certains carreaux du damier vont être en apparence déplacés verticalement ou horizontalement. La comparaison de ce film avec l'image de l'objet non perturbée par le support chaud permettra alors de voir, image par image, où se situent les volutes d'air chaud, et donc de remonter à leur dynamique, elle-même liée à la température T du support.
Figure 6. Mise en œuvre expérimentale |
4.2 Démonstration de la mesure en vidéo
4.3 Analyse des données - Description du traitement des images
Pour chacun des films ainsi obtenus, on suit la procédure suivante :
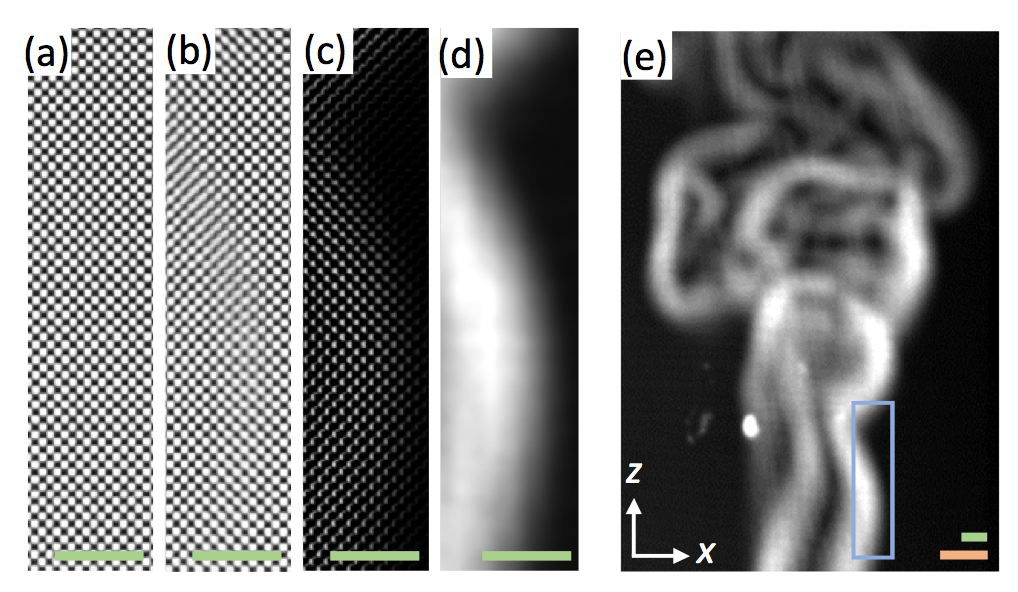
- On enregistre une image du damier à température ambiante (image de référence), figure 8 (a).
- On enregistre une image du damier en présence de la source chaude, figure 8 (b).
On soustrait l'image de référence du damier (opération réalisée à l'aide du logiciel ImageJ [2]), figure 8 (c).
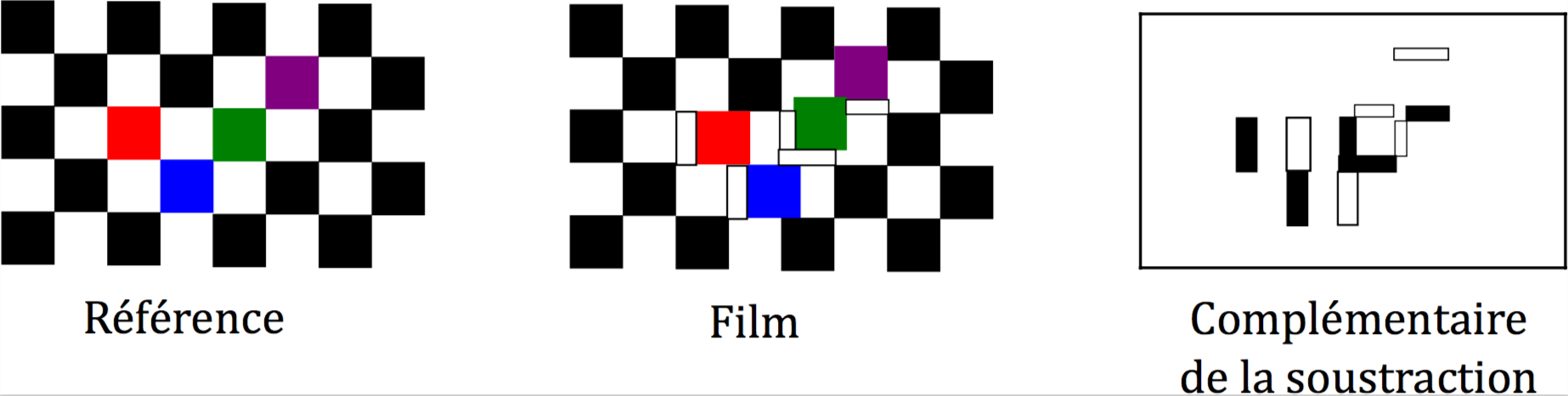
Le but de cette soustraction est de voir apparaître les déplacements,figure 9. Des figures noires apparaissent là où des carreaux initialement noirs sont devenus blancs et des figures blanches encadrées en noir là où des carreaux initialement blancs sont devenus noirs. On a des traits verticaux lorsque le carreau apparaît déplacé horizontalement, des traits horizontaux lorsque le carreau apparaît déplacé verticalement et des formes de L lorsque le carreau apparaît déplacé en diagonale.
- On applique un filtre passe-haut pour couper le motif du damier, figure 8 (d).
4.4 Mesure de la vitesse de montée des volutes
Il s'agit maintenant d'utiliser les films afin de remonter quantitativement à la vitesse de montée des volutes puis à la température du support. La description de la technique et les résultats sont proposés dans l'article suivant : Détermination de la température d'un support par méthode optique (2/2).
[1] Qu'est-ce que l'optique géométrique ? L. Dettwiller. Dunod, Paris, 1990.
[2] ImageJ, logiciel libre, codé en Java, multiplateforme, qui permet le traitement et l'analyse d'images. https://imagej.net/Welcome
Pour citer cet article :
Détermination de la température d'un support par méthode optique (1/2), Sautel, mars 2018. CultureSciences Physique - ISSN 2554-876X, https://culturesciencesphysique.ens-lyon.fr/ressource/determination-temperature1-2.xml