Activer le mode zen
Ressource au format PDF
Classification
Rayonnement, opacité et effet de serre
07/06/2021
Résumé
Comprendre et observer les notions d'opacité et de transparence au rayonnement visible et infrarouge pour aborder sereinement le principe d'effet de serre radiatif et comprendre les spectres d'émission terrestres.
Table des matières
- Introduction : objectifs
- 1. Approcher l'effet de serre avec des manipulations simples
- 2. L'atmosphère terrestre
- 3. Modélisation de l'effet de serre
- 4. Bilan “réel” et changement climatique
- 5. Analogies possibles pour l'effet de serre et son augmentation
- Conclusion
- Annexes - Spectre moyen d'émission de la Terre, issu d'observations disparates
Introduction : objectifs
Partons d'un constat : la modélisation analogique de l'effet de serre est très difficile. De nombreuses expériences qui circulent, permettant de montrer une augmentation de température, ne montrent pas l'effet de serre comme il agit sur Terre.
Revenir aux fondamentaux des interactions rayonnement/matière permet de faire des manipulations simples et scientifiquement robustes avec des paramètres fixes, une variable, des témoins, etc. Ces manipulations touchent directement aux notions de rayonnement thermique, d'équilibre thermique, de transparence et d'opacité aux rayonnements (sur des matériaux condensés).
Passer ensuite à l'effet de serre terrestre demande l'effort supplémentaire de transposer ces notions au sol et à l'atmosphère en considérant l'équilibre thermique vis-à-vis du rayonnement dans le cadre d'un modèle uniquement radiatif (donc simplifié). On peut ensuite utiliser ce modèle pour comprendre les observations du rayonnement terrestre vu de l'espace. Enfin, on peut introduire une augmentation de CO2 afin de prédire ses conséquences !
1. Approcher l'effet de serre avec des manipulations simples
1.1 Des expériences qui ne représentent pas l'effet de serre mais sont malheureusement proposées pour l'illustrer
Deux expériences (trop) classiques sont rapidement rappelées.
Expérience 1 : 2 cristallisoirs à fond noir + 2 lampes + 2 sondes thermiques + une plaque de verre recouvre l'un des cristallisoirs, figure 1. On allume les lampes (en respectant une mise en place la plus semblable possible), on mesure la température et on observe que pour le cristallisoir avec le couvercle de verre la température est plus importante.
Dans les 2 cristallisoirs on chauffe le fond noir des cristallisoirs, qui chauffe l'air. L'air moins dense monte et peut, soit petit à petit s'échapper et être remplacé par de l'air plus froid (pas de “couvercle”), soit rester piégé. Avec la plaque de verre, l'air du cristallisoir se réchauffe plus car l'air ne se refroidit qu'au contact de la plaque de verre, ce qui ne refroidit que peu l'air du cristallisoir par rapport à un apport d'air extérieur. L'effet observé n'est pas l'effet de serre “atmosphérique” mais un réchauffement de serre de jardinier par limitation physique de la convection (l'air chaud ne peut pas s'échapper)… même si parfois la plaque de verre est présentée comme un analogue de l'atmosphère car opaque aux infrarouges… mais cette expérience fonctionne aussi avec une plaque plastique transparente aux infrarouges.
Rappelons aussi que les ampoules “anciennes” à filament de tungstène produisent beaucoup d'infrarouge et chauffent donc les installations décrites aussi par le dessus (et pas seulement en chauffant le fond noir), plaque de verre comprise… L'atmosphère ne chauffe pas, elle, par le dessus.
Expérience 2 : 2 cristallisoirs à fond noir + 2 lampes + 2 sondes thermiques + l'un des cristallisoirs est enrichi en CO2 (bombe, cartouche de CO2, air expiré…), figure 2. On allume les lampes, on mesure la température et on observe que pour le cristallisoir enrichi en CO2 la température est plus importante.
Si la température dans le cristallisoir qui contient du CO2 est plus importante, c'est encore lié à une différence de convection. Le CO2 est plus dense que l'air, il faut donc que l'air enrichi en CO2 du cristallisoir soit plus chaud pour commencer à s'échapper et être remplacé par de l'air ambiant, comme dans le cristallisoir non enrichi qui, lui, voit l'air s'échapper plus tôt (à plus basse température). La température plus haute observée est, là encore, liée à la convection thermique non pas empêchée mais nécessitant une température plus haute pour commencer à permettre l'arrivée d'air ambiant plus frais dans le cristallisoir.
Ces deux manipulations simples montrent l'effet attendu “ça chauffe plus d'un côté que de l'autre” et du côté “attendu”… du fait d'effets convectifs mais pas à cause d'un effet radiatif comme pour l'effet de serre “atmosphérique”.
1.2 Retour aux fondamentaux avec des manipulations simples
Impossible de comprendre l'effet de serre si l'on n'a pas saisi les bases des interactions rayonnement/matière.
Face à un rayonnement, un matériau peut être transparent ou opaque et, dans ce dernier cas, absorber ou réfléchir le rayonnement. Ces propriétés dépendent de la longueur d'onde du rayonnement considéré.
Nous allons observer ce phénomène à l'aide de solides courants soigneusement choisis. On transposera à l'atmosphère en “évitant” la physique plus complexe des interactions rayonnement/gaz.
Pour simplifier nous allons comparer : rayonnement visible (lumière du Soleil, d'une lampe fluo ou LED qui l'imite) et rayonnement infrarouge ”thermique” – gamme de 4-5 à 25 μm ou 8 à 15 μm selon les définitions (émis par un corps ”chaud”, dans une gamme de température partant de la température ambiante jusqu'à 100°C).
1.2.1 Matériaux, matériel
On utilise une tasse, une bouilloire et de l'eau. La tasse remplie d'eau chaude constitue le corps chaud émetteur d'infrarouge thermique pour les expériences.
L'observation est réalisée avec une caméra hybride visible/thermique, figure 3. La caméra utilisée ci-après est une Seek thermal SQ-AAA (environ 800 €, il existe une version de moindre résolution à environ 600 €). La marque FLIR propose des caméras similaires ou des modules pour smartphone Android ou Apple à moins de 400 € (à brancher sur le connecteur du smartphone). D'autres appareils moins chers existent mais ne permettent pas forcément d'extraire photographies et vidéos (appareils pour professionnels travaillant dans l'isolation thermique, la recherche de pièces mécaniques en surchauffe, etc.).
Source - © 2021 Seek thermal Figure 3. Caméra visible / thermique prenant photographies et vidéos Ce type de caméra thermique a 2 objectifs et 2 capteurs alignés : un visible, classique, à assez bonne résolution (640x480 pixels ici) et un thermique à résolution moindre (320x240 ici) qui permet de “coloriser” l'image visible, conservant ainsi les détails morphologiques sous l'information thermique donnée par la coloration. Attention, le capteur thermique ne fonctionne pas comme le capteur visible, qui “compte” les photons reçus par effet photoélectrique. C'est une matrice de petites thermistances qui s'équilibrent très vite en température avec le rayonnement infrarouge reçu (on parle aussi de microbolomètres). C'est la résistance électrique des capteurs qui est mesurée et traduite en température. On ne ”voit” donc pas directement les photons infrarouges reçus. |
Dans la première expérience, on utilise du plexiglas (PMMA), du polyéthylène (PE) basse densité transparent (emballage, sac congélation), du PE noir (sac poubelle) et de l'aluminium (feuille d'emballage de chocolat, par exemple). Dans la seconde expérience, on utilise plexiglas et aluminium et des supports pour les tenir en place.
1.2.2 Expérience 1 – Comportement individuel des matériaux : opacité et transparence
Une tasse remplie d'eau chaude à environ 90°C (bouilloire portée à ébullition) est observée avec le capteur visible ou thermique et on fait passer les matériaux entre tasse et caméra, figures 4 et 5. Si la tasse est cachée le matériau est opaque, si la tasse est visible le matériau est transparent aux longueurs d'ondes observées.
Figure 4. La tasse chaude en visible En lumière visible on voit la tasse, ses couleurs et dessins. | Figure 5. La tasse chaude en infrarouge (IR) En IR on voit le contour de la tasse et la couleur correspond à la température de la surface (qui correspond à une certaine longueur d'onde domimante d'IR thermique). La gamme de couleurs peut être définie en fixant les couleurs extrêmes (ici de 20°C pour le noir à 83°C pour le blanc) : cette échelle de couleurs est gardée fixe pendant tout le film (échelle exportée sur les photos mais pas sur les vidéos). |
Sur la figure 6 nous proposons une vidéo de l'expérience avec différents matériaux en guise d'écran.
Source - © 2021 Olivier Dequincey - Patrick Thollot - ENS de Lyon Figure 6. Expérience filmée : opacité-transparence de matériaux dans le visible-infrarouge |
On s'intéresse ici à l'illustration du pouvoir de transparence ou d'opacité entre le rayonnement visible et l'infra-rouge. Ces propriétés dépendent des matériaux mais aussi leur état de surface. Dans la suite de cet article, on considère des états de surface lisses, correspondant aux images expérimentales enregistrées.
Tableau 1. Opacité / transparence des matériaux testés
Matériau | Visible | IR thermique | |
Polyéthylène transparent (PE basse densité) | transparent | transparent | |
Plexiglas (PMMA) | transparent | opaque (absorbe **) | |
Aluminium | opaque (réfléchit *) | opaque (réfléchit **) | |
Polyéthylène noir (PE) | opaque (absorbe *) | transparent |
* si l'on peut se cacher derrière aluminium et sac plastique noir, notre image nous est renvoyée par l'aluminium (réflexion) mais pas par le sac plastique noir (absorption).
** dans l'expérience 2, on peut voir la forte réflexion des IR thermiques par l'aluminium alors que l'absorption prédomine pour le plexiglas (faible réflexion détectée… et réémission mise en évidence).
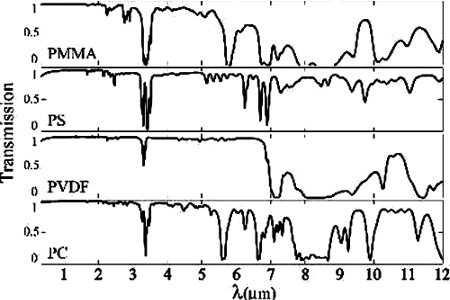
La figure 7 présente les spectres de transmission du PMMA (plexiglas) et autres plastiques PS (polystyrène), PVDF (polyvinylènedifluor) et PC (polycarbonate). On constate que le plexiglas absorbe parfois complètement de nombreuses longueurs d'ondes de cet intervalle “thermique”.
Source - © 2006 2006 Y. Gao et al.
Y. Gao, N. Guo, B. Gauvreau, M. Rajabian, O. Skorobogata, E. Pone, O. Zabeida, L. Martinu, C. Dubois, M. Skorobogatiy, 2006. Consecutive solvent evaporation and co-rolling techniques for polymer multilayer hollow fiber preform fabrication, Journal of Materials Research, 21, 2246–2254
1.2.3 Expérience 2 – Opacité aux IR thermiques avec réflexion ou absorption/réémission
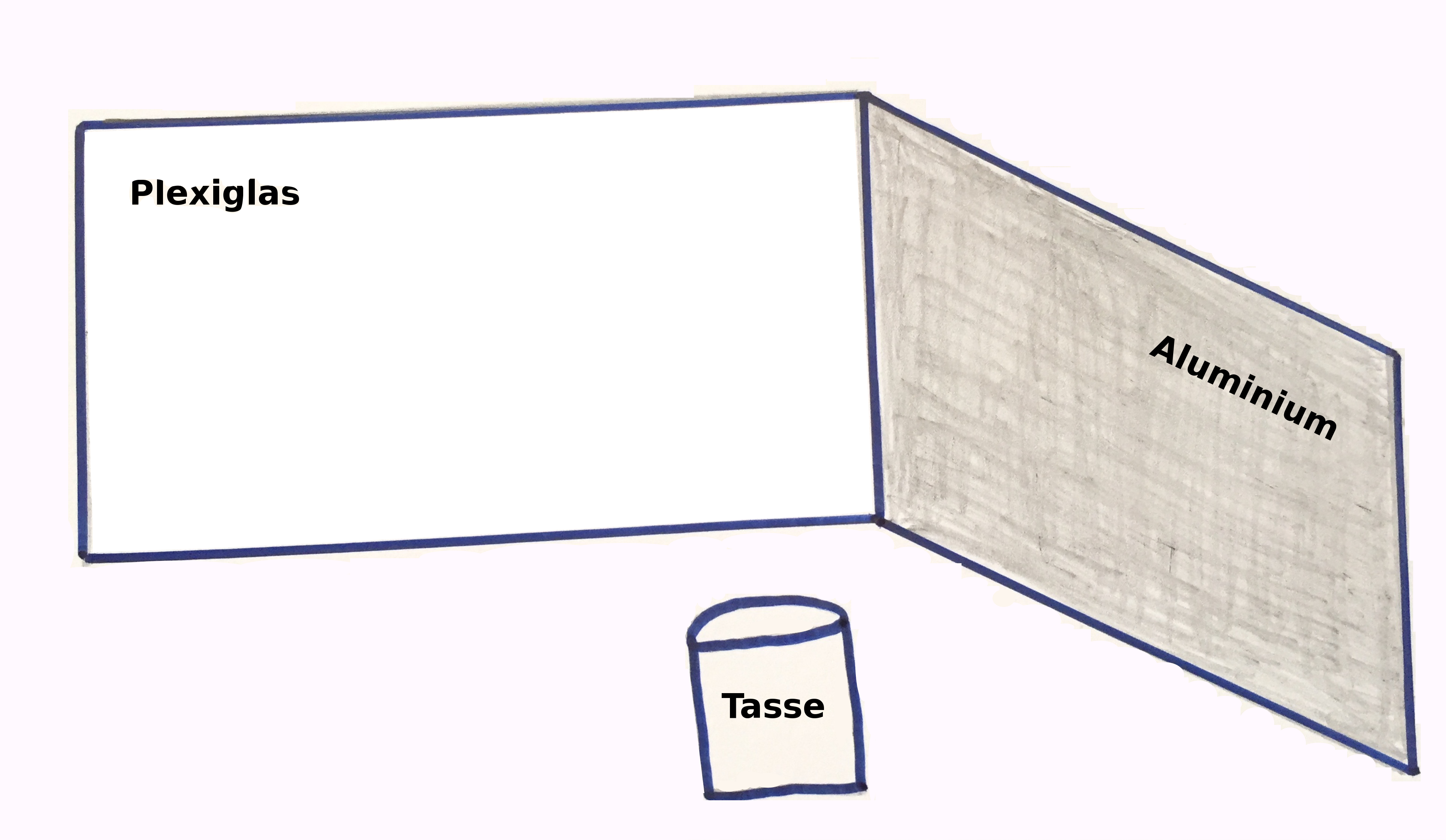
Deux parois, l'une en plexiglas et l'autre en aluminium, forment un angle légèrement obtus (pour éviter les réflexions d'une paroi vers l'autre) et une tasse remplie d'eau chaude est placée dans l'angle, à environ 2 cm des parois au plus près, figure 8. On va observer l'opacité à l'IR thermique différente pour l'aluminium (réflexion) et pour le plexiglas (essentiellement absorption et réémission).
Figure 9. La tasse chaude en place en visible On voit que l'opacité de l'aluminium au visible montrée dans l'expérience 1 (et aussi dans celle-ci) s'accompagne d'une réflexion de ce rayonnement puisque l'image “visible” de la tasse est renvoyée vers la tasse. | Figure 10. La tasse chaude en place en IR On voit que l'opacité de l'aluminium à l'IR thermique montrée dans l'expérience 1 (et aussi dans celle-ci) s'accompagne d'une réflexion de ce rayonnement puisque l'image “thermique” de la tasse est renvoyée vers la tasse. Pour le plexiglas, une légère réflexion est décelée (une image aux tons violets “froids”). L'opacité à l'IR thermique du plexiglas est donc essentiellement liée à l'absorption de l'IR non transmis. Ici les couleurs vont de 18°C (noir) à 73°C (blanc), échelle de couleur constante pour tout le film. |
Source - © 2021 Olivier Dequincey - Patrick Thollot - ENS de Lyon Figure 11. Expérience filmée : opacité IR et réflexion ou absorption / réémission Depuis le côté de la tasse, on observe (0min40s) pour l'IR thermique que le plexiglas ne réfléchit pas (ou très peu), alors que l'aluminium oui. De “derrière” (1min), le plexiglas ne transmet pas l'IR, l'aluminium non plus. Après 2 minutes (et plus), un rayonnement thermique apparait derrière le plexiglas (2min48s), mais pas derrière l'aluminium (2min30s). Si l'on retire la tasse (3min15s), le rayonnement thermique derrière le plexiglas persiste. Il est aussi visible devant (3min50s). Il n'est donc pas transmis, mais propre : le plexiglas a absorbé le rayonnement de la tasse et a chauffé, contrairement à l'aluminium qui l'a réfléchi. Le plexiglas, réchauffé, réémet un rayonnement IR thermique “des deux côtés” : “vers l'extérieur” et “vers la tasse”. (La table a elle aussi chauffé sous la tasse). On voit bien en déplaçant la plaque de plexiglas (7min15s) que le rayonnement IR est propre à la plaque car la tache thermique se déplace avec la plaque (ce n'est pas de la réflexion). Téléchargez une version chapitrée (7min28s, 22 Mo) au format webm ou mp4. | |
Conclusion importante : comme nous le voyons dans cette expérience, un corps opaque qui absorbe du rayonnement thermique, chauffe et en émet un rayonnement à son tour.
Un corps n'a pas nécessairement besoin d'être chauffé au préalable, il peut aussi être le siège d'une réaction chimique, de radioactivité…
De plus, un corps qui ne chauffe pas réfléchit ou transmet le rayonnement. On approche ainsi la loi du rayonnement de Kirchhoff : à l'équilibre thermique les flux d'absorption et d'émission/transmission sont égaux.
2. L'atmosphère terrestre
2.1 Opacité et transparence de l'atmosphère terrestre
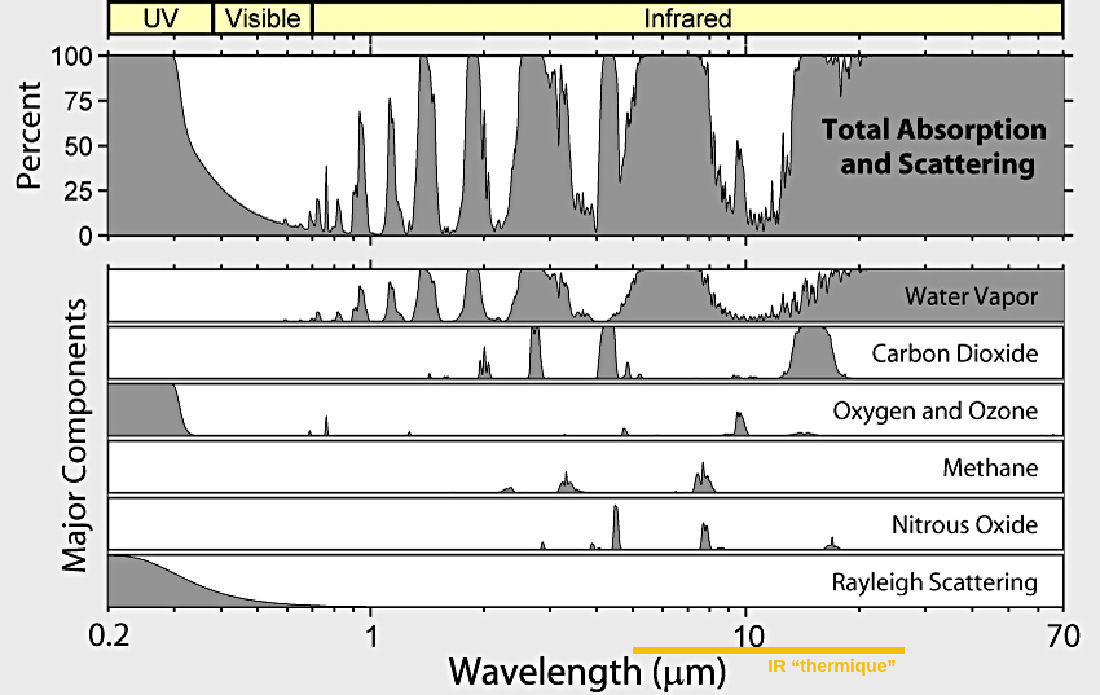
L'atmosphère est opaque (du fait de l'absorption et, pour certaines longueurs d'ondes, de la diffusion – scattering) aux UV de haute énergie (courtes longueurs d'onde) et à l'essentiel des IR thermiques. Elle est par contre fortement transparente au rayonnement visible et à une bande d'IR vers 8-13 µm, appelée « fenêtre » infrarouge (coloré en jaune sur la figure 12).
Les contributions respectives des différents gaz à effet de serre (vapeur d'eau, dioxyde de carbone, méthane, protoxyde d'azote) et du phénomène de diffraction sont détaillées dans la figure 12.
Source - © 2007 D'après Global Warming Art
L'atmosphère terrestre se rapproche du comportement du plexiglas : transparente au visible, opaque aux infrarouges “thermiques” (> 5 µm ) sauf vers 8-13 µm où elle est transparente aux infrarouges. On parle de « fenêtre » infrarouge de l'atmosphère.
2.2 Rappels sur le corps noir
Un corps noir est un corps qui absorbe, sans la réfléchir ni la diffuser, toute l'énergie électromagnétique qu'il reçoit. Il reçoit de l'énergie et s'il n'en émettait pas, sa température augmenterait indéfiniment... Ceci est irréaliste, un corps noir réémet donc l'énergie qu'il a absorbée sous forme de rayonnements électromagnétiques, figure 13.
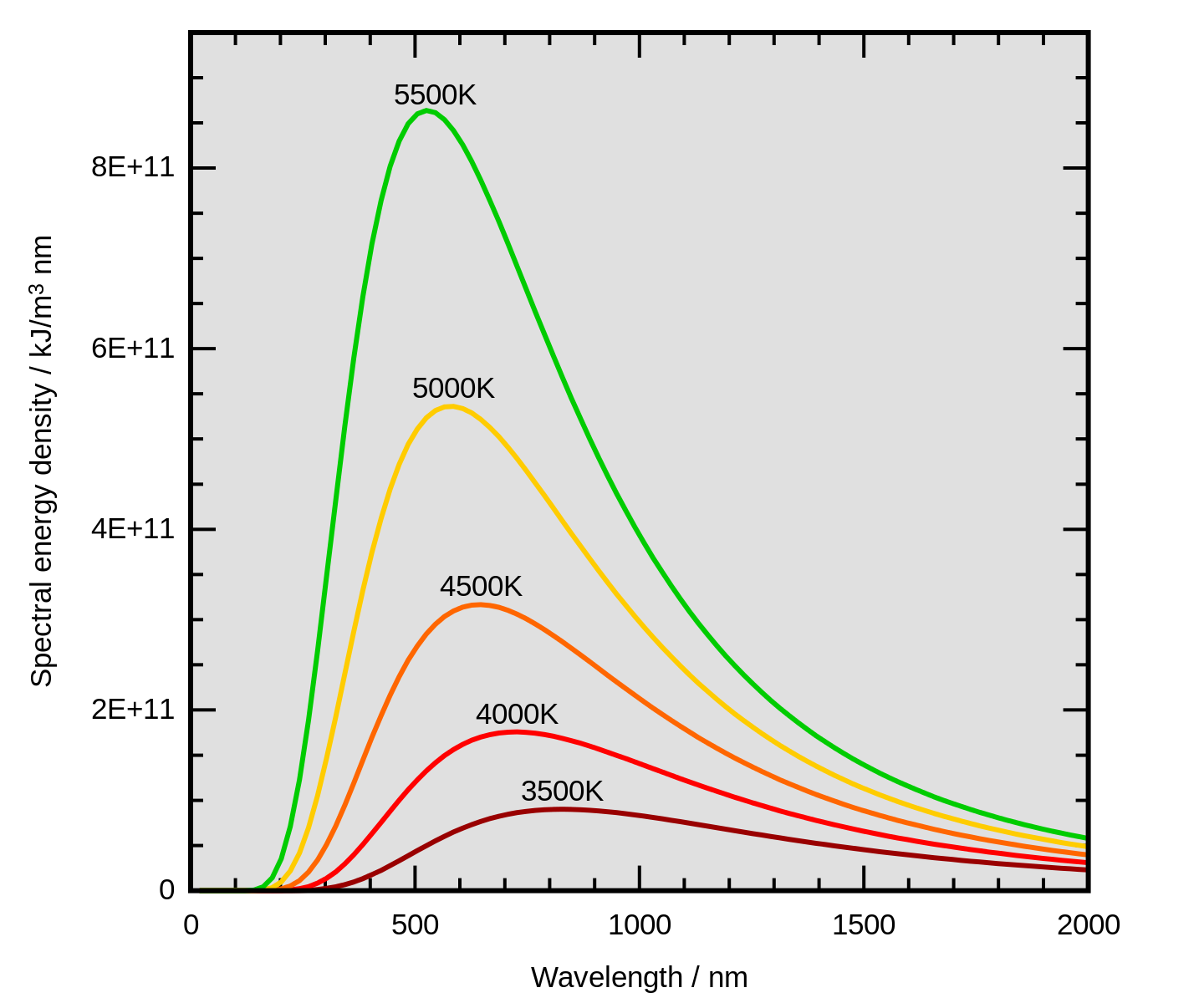
La quantité d'énergie réémise dépend de sa température. Ainsi, il existe une "loi de rayonnement du corps noir" qui donne la valeur de l'énergie émise en fonction de la température du corps noir (loi de Stefan-Boltzmann) : F = σ.T4, avec F, densité de flux d'énergie émise par la surface du corps noir (W.m−2), T la température absolue (K), et σ la constante de Stefan-Boltzmann (~5,67.10−8 W.m−2.K−4).
Plus la température est élevée, plus l'énergie réémise est importante.
Le rayonnement électromagnétique émis est un spectre avec un maximum de luminance à une longueur d'onde λmax dépendant elle aussi de la température de surface du corps noir selon la loi Wien : λmax ≈ 2,898.10−3 / T, avec λ en m et T en K. Plus la température augmente plus le “pic” d'énergie est dans les courtes longueurs d'ondes. Application numérique : la surface du Soleil est à une température moyenne d'environ 5800 K, son “pic” est donc vers 5.10−7 m, soit 0,5 μm ou 500 nm (dans le spectre visible, spectre allant de 380 à 780 nm), la surface d'un corps à 20°C (293 K) voit son pic aux alentours de 9,9.10−6 m soit 9,9 μm (dans l'infrarouge thermique).
Plus la température est élevée, plus l'énergie émise (l'aire “sous la courbe”) est élevée.Plus la température est élevée, plus le “pic” est décalé vers les courtes longueurs d'ondes. Source Wikimedia. |
2.3 Spectre moyen d'émission terrestre comparé au spectre du corps noir
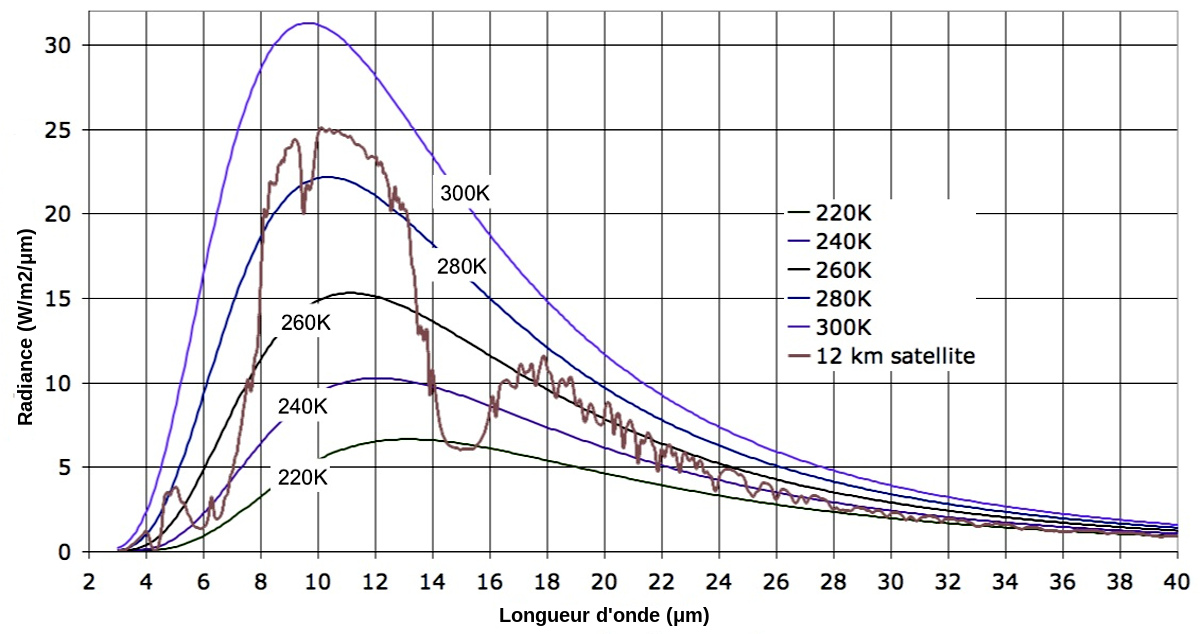
Le spectre moyen de la Terre n'est pas celui d'un corps noir mais son enveloppe extérieure est proche du spectre de corps noir à environ 288 K (voir vers 10-12 μm) et son enveloppe inférieure approche plutôt un spectre pas loin de 220 K (voir à 6 et vers 14-15 μm), figure 14 (le spectre moyen de la Terre est en marron).
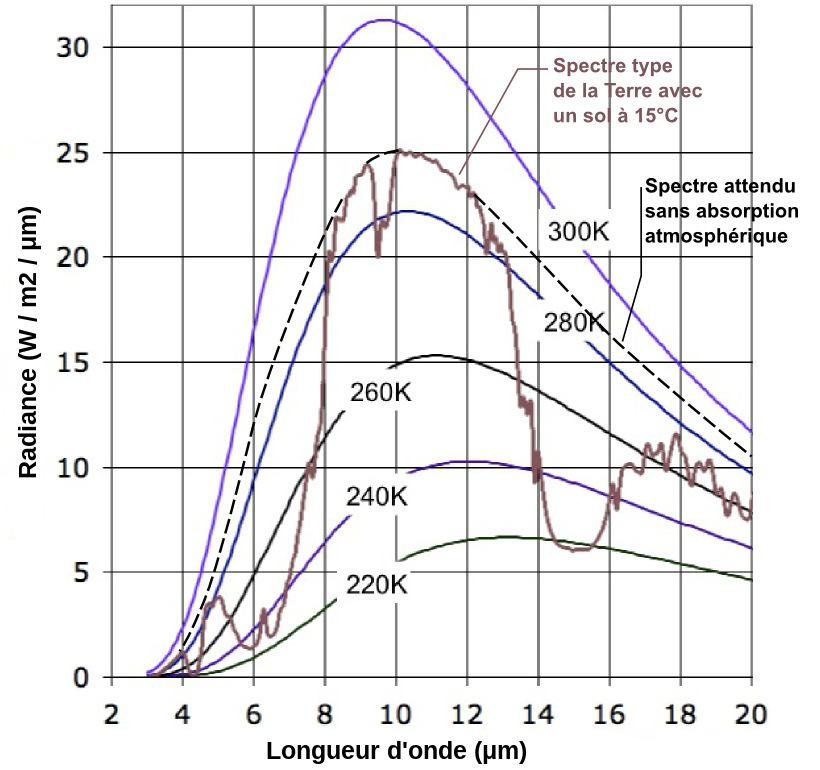
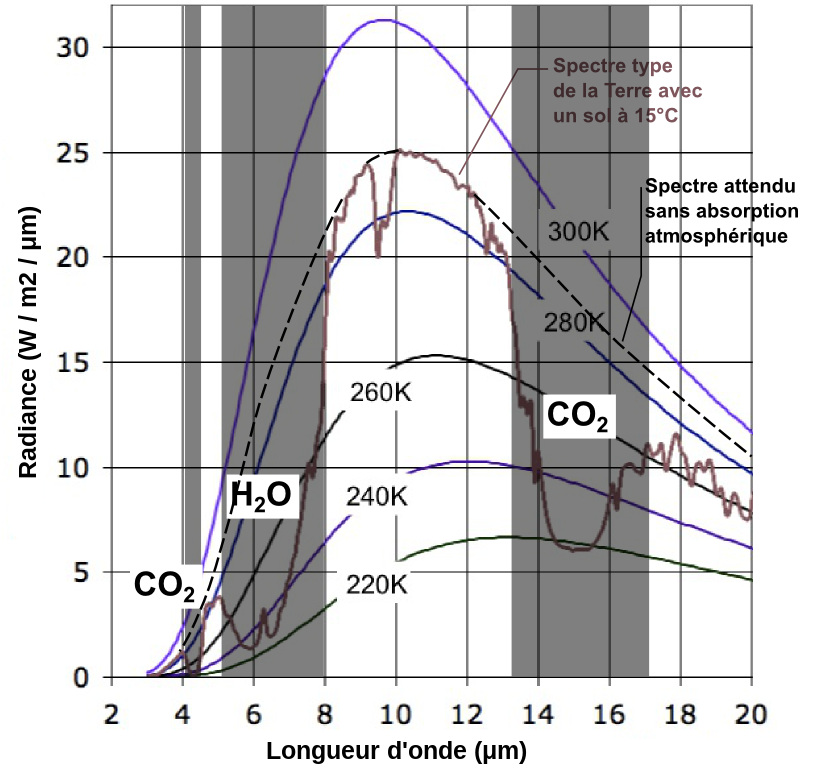
Le spectre d'émission de la Terre coïncide, vers 9 μm et pour la bande 10-12 μm, avec le spectre théorique d'un corps noir de température de surface égale à 15°C (figure 15) et les “creux” correspondent aux bandes d'absorption principales d'H2O et de CO2 (figure 16).
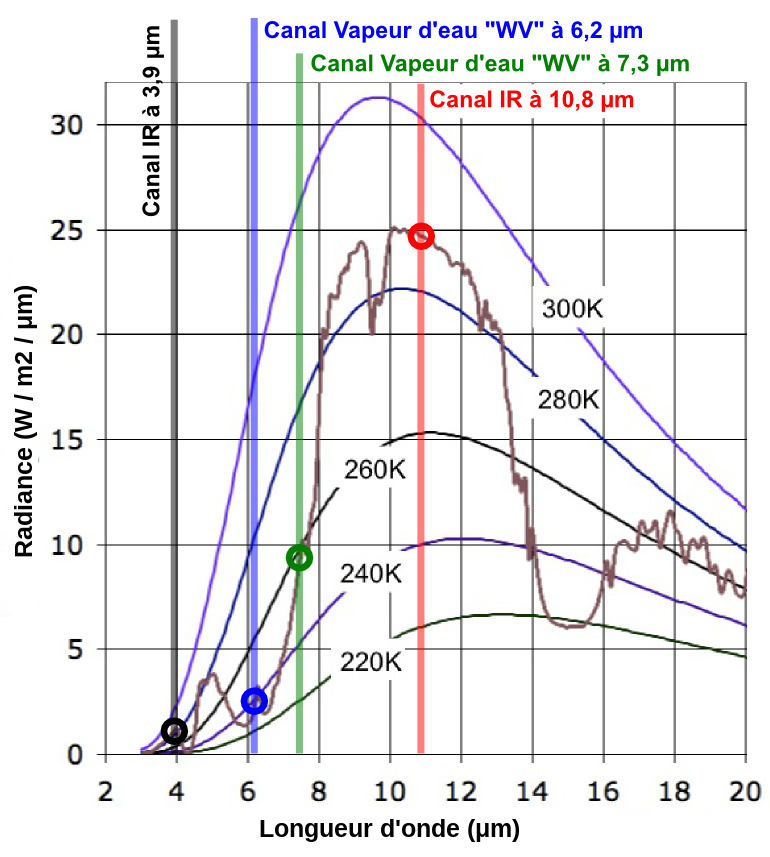
Les principaux canaux IR d'observation permettent de se focaliser sur des aspects différents, figure 17. Le canal à 3,9 μm renseigne sur le sol (c'est un fenêtre de faible énergie), les canaux WV (water vapor) à 6,2 et 7,3 μm “regardent” la vapeur d'eau (le canal à 6,2μm, au cœur de la bande de la vapeur d'eau observe le sommet de la masse d'air humide, alors que le canal à 7,3μm, plus à la marge de cette bande d'absorption, “ausculte” plus en profondeur dans l'air humide), alors que le canal à 10,8 μm donne une “image” du sol terrestre.
Les spectres d'émission de la Terre montrent des disparités spatiales sur l'ensemble du globe. Pour ce point plus précis, on se repportera en annexe pour les consulter.
3. Modélisation de l'effet de serre
3.1 Bilan radiatif simplifié de la Terre
Nous allons construire un modèle de Terre à partir des trois hypothèses suivantes :
- L'atmosphère a un comportement composite face au rayonnement : transparente au visible, partiellement opaque au thermique (opacité dans les bandes où les GES absorbent).
- Les transferts d'énergie sont supposés uniquement radiatifs. C'est le cas avec l'espace ; c'est une simplification avec le sol et à l'intérieur de l'atmosphère.
- Il y a équilibre thermique : tout ce qui est absorbé est émis.
On ajuste ce modèle avec 3 paramètres d'entrée fixés, mesurables sur Terre :
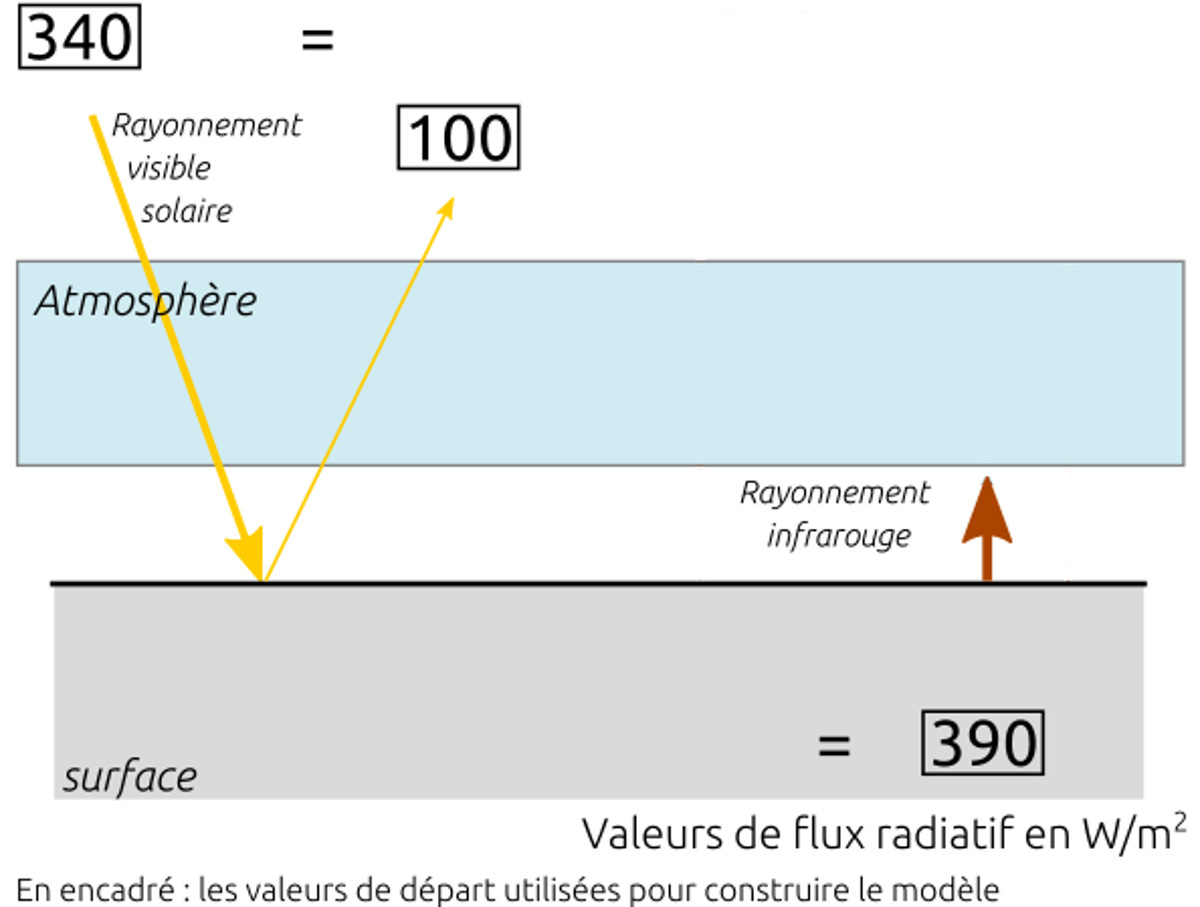
- un rayonnement visible d'une puissance de 340 W/m² arrive au sommet de l'atmosphère (mesure par satellite tourné vers le Soleil),
- un rayonnement visible d'une puissance de 100 W/m² est réfléchi par la Terre (mesure par satellite tourné vers le sol),
- la surface de la Terre est à 15°C de moyenne et se comporte comme un corps noir ; la Terre émet donc 390 W/m² de rayonnement infrarouge thermique.
À partir de ce schéma et de ces données, complétons le bilan, à l'aide des figures 18 à 21.
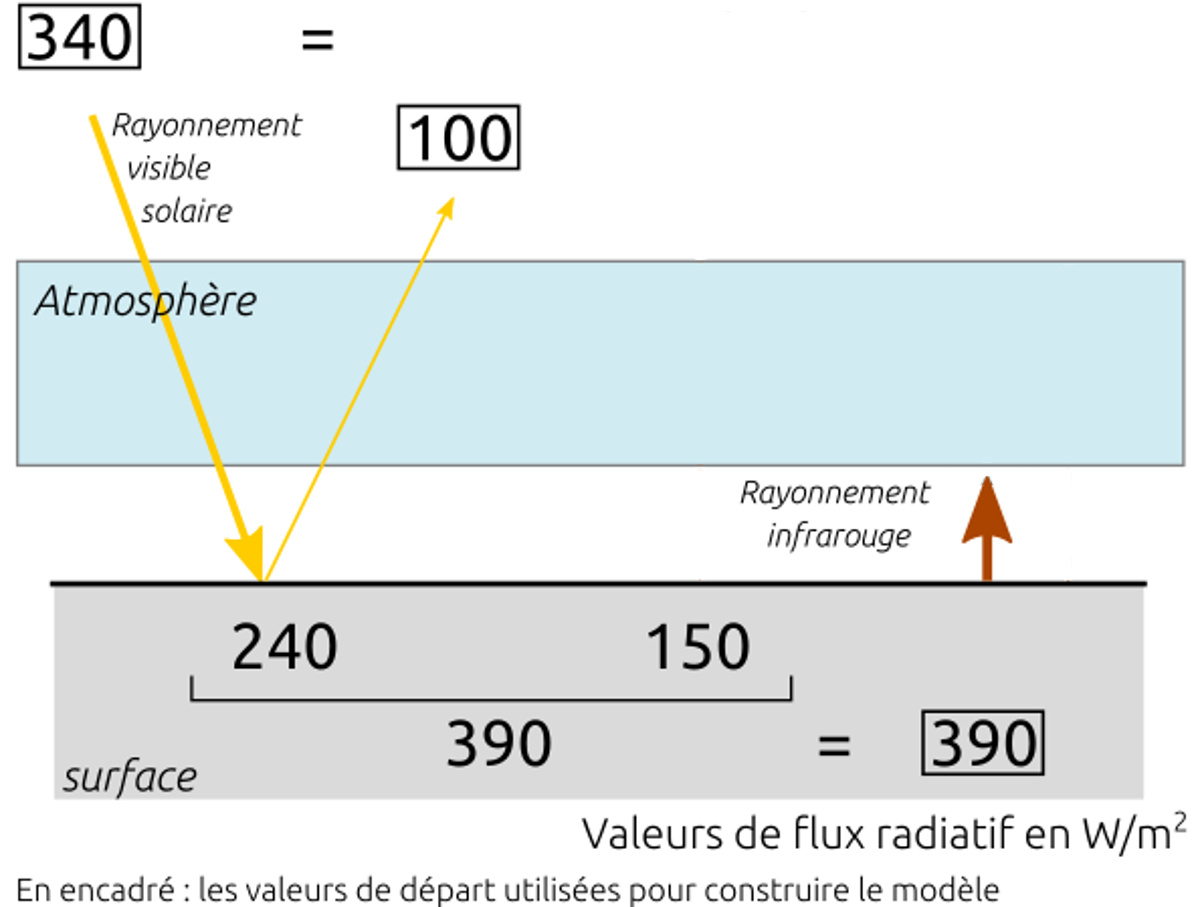
Figure 18. Données de départ pour le bilan radiatif Les 3 milieux (espace / atmosphère / surface) et les 3 données de départ sont représentés. | Figure 19. Bilan radiatif complété pour le sol À partir des données de départ, on déduit la puissance absorbée par le sol et celle reçue de l'atmosphère. |
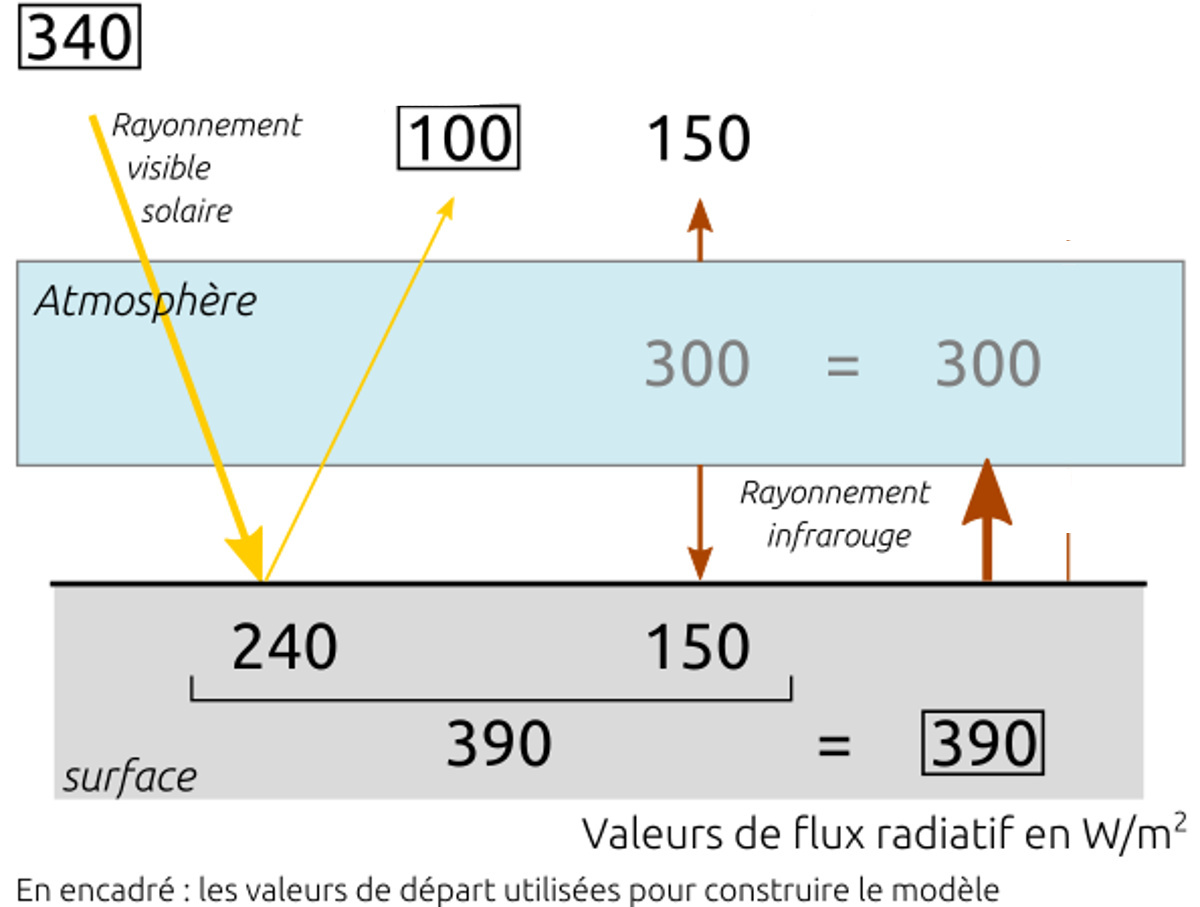
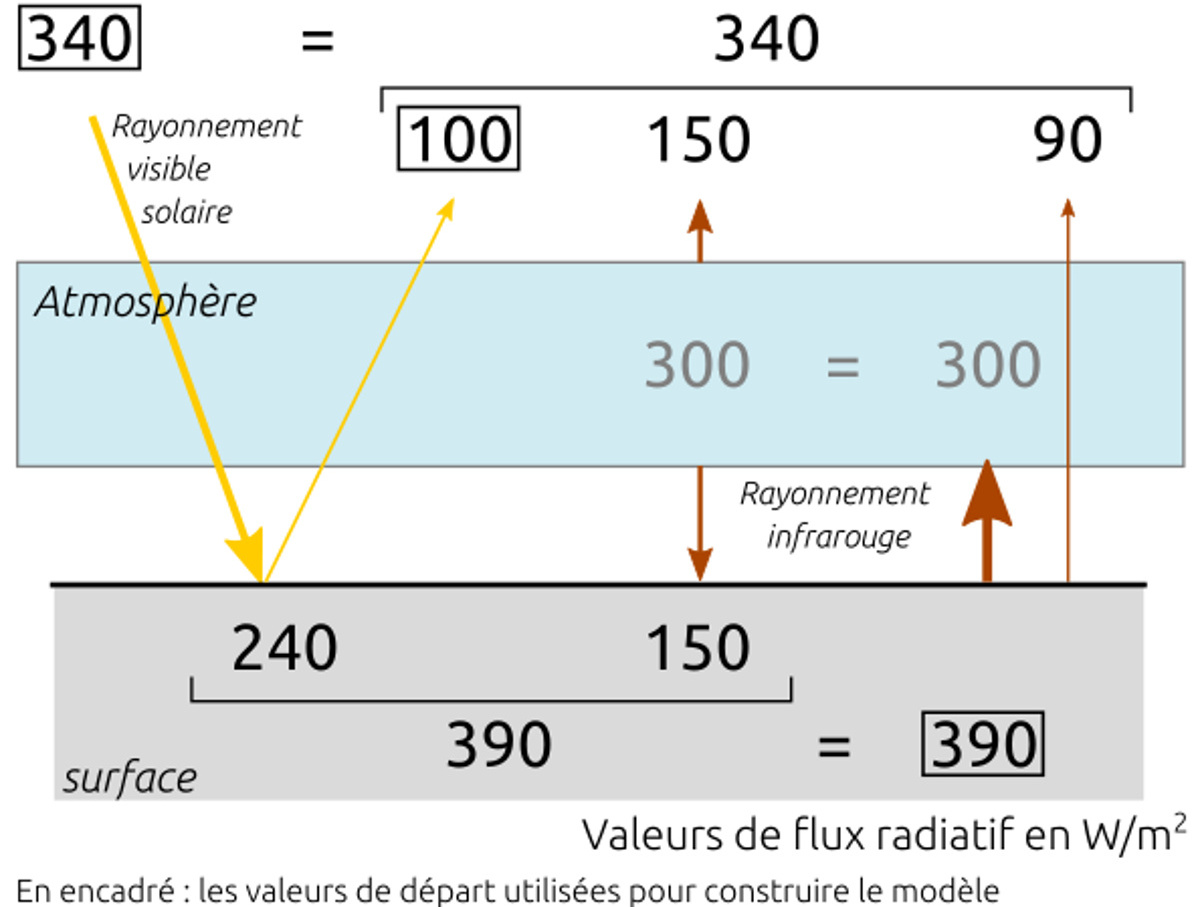
Figure 20. Bilan radiatif complété pour l'atmosphère L'atmosphère émet autant vers l'espace que vers le sol et reçoit son énergie du sol. | Figure 21. Bilan radiatif final équilibré L'atmosphère n'absorbe qu'une partie du rayonnement infrarouge du sol, le reste est émis vers l'espace. |
Puisque le rayonnement solaire de 340 W/m² est réfléchi à hauteur de 100 W/m², on en déduit que le sol reçoit 340 − 100 = 240 W/m² d'énergie sous forme de rayonnement visible issu du Soleil. Comme le sol émet 390 W/m², c'est qu'il reçoit aussi 390 − 240 = 150 W/m² d'énergie de l'atmosphère (seule autre source).
L'atmosphère émet donc 150 W/m² vers le sol sous forme d'infrarouge thermique. L'atmosphère ”chaude” émet son rayonnement de manière égale dans toutes les directions, donc elle émet autant ”vers le haut” que “vers le bas”. Au total, l'atmosphère émet donc 300 W/m². Étant transparente au rayonnement visible, l'atmosphère reçoit donc cette énergie sous forme infrarouge de l'autre source, la surface de la Terre.
Si le sol émet 390 W/m² et que 300 W/m² sont absorbés par l'atmosphère, c'est que le reste 390 − 300 = 90 W/m² est émis directement vers l'espace (fenêtre infrarouge). Vérifions alors les flux au sommet de l'atmosphère : arrivent 340 W/m² de rayonnement visible, repartent 100 W/m² de visible réfléchi, 150 W/m² d'infrarouge émis par l'atmosphère et 90 W/m² émis par la surface de la Terre ; on a bien équilibre puisque 340 = 100 + 150 + 90.
3.2 Une atmosphère réelle non isotherme, plus ou moins opaque
Une simplification majeure du modèle radiatif présenté ici est l'hypothèse d'une atmosphère isotherme. En réalité, la température décroit avec l'altitude (jusqu'à 20 km d'altitude correspondant à plus de 95 % de la masse de l'atmosphère). Le sommet de l'atmosphère, plus froid, rayonne moins d'IR thermique que sa base, plus chaude !
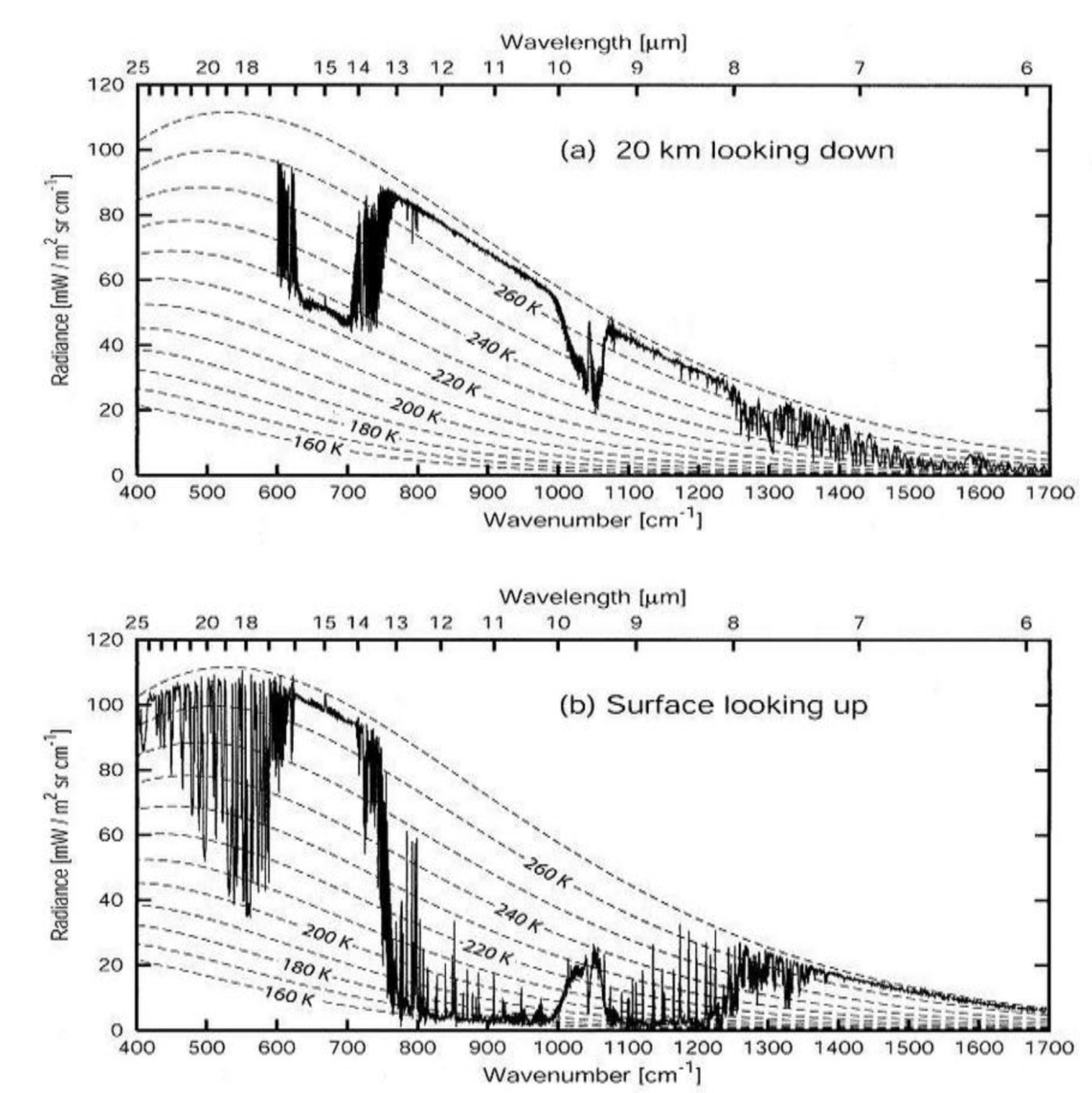
Ceci se voit bien lorsqu'on compare les mesures effectuées depuis un avion ou un ballon-sonde à 20 km d'altitude (“sommet” de l'atmosphère), et depuis la surface du sol, à l'aplomb d'un même lieu à un instant donné, figure 22.
Source de la figure originale,
G.W. Petty, 2006. A First Course in Atmospheric Radiation, Sundog Publishing, Madison, Wisconsin, 452p. ISBN-13:978-0-9729033-1-8 [pdf chapitre 8]
L'atmosphère vue depuis 20 km d'altitude (ballon-sonde), montre un spectre identique à celui vu de l'espace (la quasi-totalité de la masse de l'atmosphère étant sous 20 km d'altitude). Aux longueurs d'onde où l'atmosphère est transparente, on voit le sol du sommet de l'atmosphère et l'espace depuis la surface de la Terre. Aux longueurs d'onde où l'atmosphère est opaque on voit le ”sommet” de la masse d'air opaque, plus froid, donc moins rayonnant que le sol, et, en regardant de la Terre vers l'espace, la “base” de la masse d'air opaque, chaude, plus rayonnante l'espace et que son “sommet”. Différence fondamentale par rapport à la plaque de plexiglas et au modèle radiatif simple : l'atmosphère ne rayonne pas autant à sa base et à son sommet.
3.3 Modèle numérique simple pour montrer la conséquence de l'ajout de gaz à effet de serre : exemple du CO2
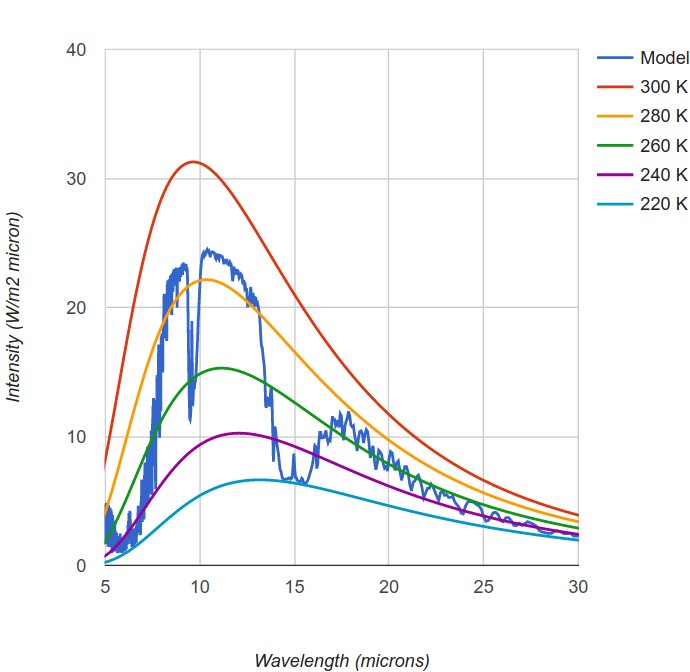
La figure 23 présente une simulation du spectre d'émission de la Terre (représenté en bleu), correspondant à l'état « pré-industriel ». Les résultats donnent, dans ce modèle, une différence de température au sol de −0.6 K par rapport à aujourd'hui.
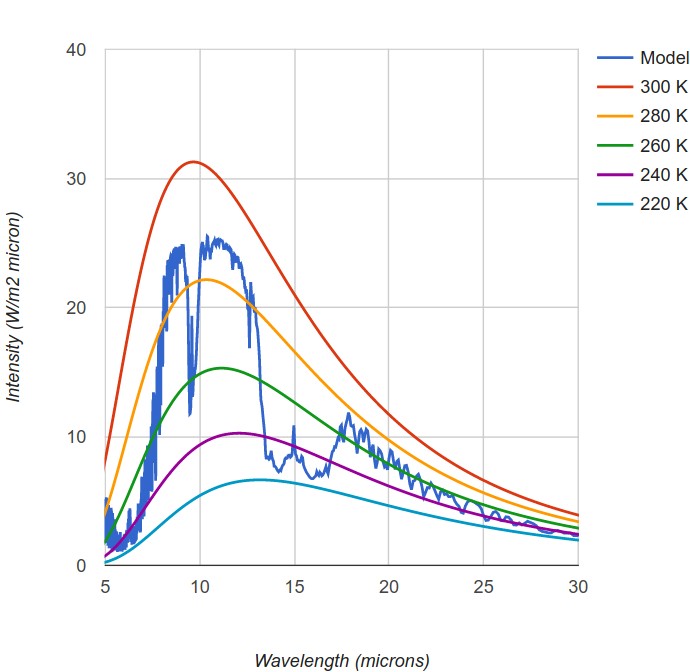
Sur la figure 24, le spectre d'émission est représenté avec une concentration 10 fois plus élevée (2 800 ppm) de CO2. Le rayonnement thermique du sol dans la fenêtre infrarouge équivaut à un réchauffement du sol de 4,2 K par rapport à la simulation à 280 ppm (état « pré-industriel »).
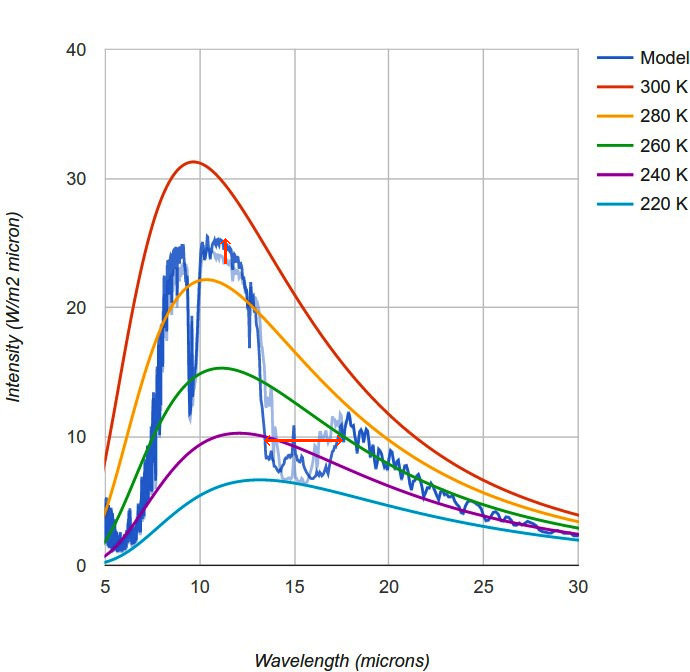
L'élargissement de la bande d'absorption du CO2 autour de 15 μm correspond à une moindre émission d'énergie de l'atmosphère terrestre vers l'espace, figure 25. Cette baisse est “compensée” (même apport solaire pour les deux simulations) par l'augmentation de l'émission d'énergie venue du sol (plus chaud) par la fenêtre atmosphérique (par exemple, vers 12 μm).
Attention, ces 2 simulations, qui estiment à +4,2 K l'écart de température au sol sont faites avec un modèle 1D, purement radiatif, qui ne prend en compte ni les rétroactions diverses (notamment l'augmentation de vapeur d'eau à priori consécutive à l'augmentation de température), ni les fortes inégalités spatiales et temporelles (latitudes, saisons).
4. Bilan “réel” et changement climatique
Des observations et mesures réelles permettent de proposer un schéma du bilan radiatif de la Terre, tel celui proposé par le laboratoire NASA Langley Research Center, figure 26.
Source - © 2019 NASA-LaRC
Figure 26. Bilan radiatif terrestre moyen, issu de mesures sur 10 années
Le poster d'origine Earth's Energy Budget (version mise à jour en 2019) possède aussi un document d'accompagnement (Earth’s Energy Budget: A Story).
On remarque qu'au sommet de l'atmosphère arrive un flux de 340,4 W.m−2 alors qu'il ne repart vers l'espace que 99,9 + 239,9 = 339,8 W.m−2. Le système Terre-atmosphère absorberait au final 0,6 W.m−2 ; il se réchaufferait donc.
Un bilan radiatif “réel” est complexe à réaliser. Qualitativement, le bilan proposé se base sur de nombreuses études menées depuis les années 1900 jusqu'à aujourd'hui. Il prend en compte tous les phénomènes physiques, actions et rétro-actions, reconnus, compris, modélisés… Ce côté qualitatif est robuste, le système climatique est bien connu aujourd'hui (on arrive à comprendre les observations passées et à les “reproduire” par des modèles). Quantitativement parlant, un bilan chiffré est complexe à réaliser compte tenu des nombreux paramètres à mesurer, des différents outils utilisés, et des marges d'erreurs propres à chaque type de mesure et type d'instrument. Différentes études ont porté sur l'amélioration de la qualité des mesures, mais aussi sur la comparaison de données, sur la compilation de données nouvelles pour améliorer la précision de mesures, la répétition de mesures sur plusieurs années… Certains ajustements sont aussi apportés pour assurer l'équilibre de certains transferts d'énergie… C'est le résultat de ce travail qui est présenté. Il a été remis à jour 2 fois depuis sa première publication en 2004. Un déséquilibre énergétique au sommet de l'atmosphère y est systématiquement détecté.
Sur la base de ce bilan, le système Terre-atmosphère emmagasinerait de l'énergie (0,6 W.m−2) non restituée, et se réchaufferait donc (en parfaite adéquation avec les observations).
Les bilans théoriques à l'équilibre, pour une compréhension facile des processus majeurs, correspondent à des états stationnaires dans lesquels aucun paramètre ne bouge et pour lesquels les effets de perturbations antérieures sont stabilisés.
On voit ici que de faibles perturbations relatives (0,6 sur 340,4 soit moins de 2‰) suffiraient à expliquer le changement climatique actuel (les forçages radiatifs proposés dans les modèles du GIEC sont aussi de l'ordre de quelques W.m−2 depuis le début de l'ère industrielle). Ces variations peuvent être naturelles et refléter une variation de l'insolation (distance Terre-Soleil), de l'albédo (nébulosité, neige, émissions volcaniques stratosphériques…), de l'effet de serre… Le forçage (le processus perturbateur avec conséquence énergétique) actuel est essentiellement d'origine anthropique et a pour origine l'émission de gaz à effet de serre (CO2 et CH4 principalement), émission qui, pour revenir aux modèles vus plus haut, ferme les fenêtres atmosphériques, augmente l'altitude de la limite d'opacité atmosphérique, ce qui est en cours d'être compensé par un réchauffement du sol émettant alors plus d'énergie dans les longueurs d'onde pour lesquelles l'atmosphère est transparente, avec arrivée à un nouvel état d'équilibre présentant un sol plus chaud.
5. Analogies possibles pour l'effet de serre et son augmentation
Nous proposons ici quelques analogies à l'effet de serre et à ses variations. Ce sont des "approximations" qui ne prennent pas en compte les rétroactions. Les analogies proposées cherchent à mettre en évidence qu'avec un flux entrant constant (chaleur, débit d'eau) on peut avoir une mesure de sortie variable (température, hauteur d'eau, pression). De même, un apport énergétique solaire externe constant donne une température d'équilibre au sol variable selon l'existence et l'intensité d'un effet de serre.
5.1 Une maison plus ou moins isolée
D'après la loi de Fourier, on a une densité de flux thermique, F (W.m−2), à travers les parois donnée par : F = λ . ΔT / e, avec λ la conductivité thermique des parois (W.m.K−1), e leur épaisseur (m), ΔT l'écart de température (K) entre intérieur et extérieur (T extérieure supposée fixe).
Le flux F est fixé (radiateur non thermostaté réglé sur une puissance constante) et analogue au flux de chaleur que la Terre et son atmosphère évacuent vers l'espace (= flux solaire absorbé).
On a deux façons de faire une analogie avec l'augmentation des gaz à effet de serre (GES) : soit on augmente l'épaisseur d'isolant e (“épaisseur” de GES dans l'atmosphère) soit on diminue la conductivité λ (atmosphère plus opaque). Ayant augmenté e et/ou diminué λ, le flux F étant constant, il en résulte que l'écart de température ΔT augmente. Si la température extérieure n'a pas changé, l'intérieur de la maison chauffe donc jusqu'à ce que l'augmentation de ΔT permette au flux F fixé de passer à travers les parois. À même apport de chaleur, on a une température différente selon la “facilité” d'évacuation de l'énergie vers l'extérieur.
Dans le cas de la conduction, le flux F est proportionnel à l'écart de température ΔT. Pour le rayonnement, le flux F est proportionnel à la puissance 4 de la température absolue, d'où l'écart de température Δ(T4).
Ainsi, augmenter l'épaisseur d'isolant e de sa maison de 1 % (× 1,01) multiplie ΔT (écart de température) par 1,01 : s'il fait −5°C dehors et qu'on chauffe à 15°C, l'écart de température passe de 20 à 20,2°C et il fait alors 0,2°C de plus, soit 15,2°C, après isolation. Si, pour un sol à 15°C, on augmente l'opacité de l'atmosphère de 1 %, on multiplie T (température absolue) par ≈1,0025 (racine quatrième de 1,01), et on passe de 288 K à 288,7 K, soit, dans ce cas, une augmentation de 0,7°C.
5.2 Un pommeau de douche réglable
Attention : idée délicate à faire passer car faisant d'une pression l'analogue d'une température…
Avec un même débit d'eau sortant d'un pommeau de douche (analogue du flux thermique que la Terre évacue = le flux solaire reçu), on a une pression d'eau sortant du pommeau, celle dans le pommeau, variant selon l'ouverture des trous : avec beaucoup de trous ouverts (atmosphère plus transparente au rayonnement thermique) la pression est plus faible, avec peu de trous ouverts (atmosphère plus opaque au rayonnement thermique) la pression est plus forte. La pression dans le pommeau deviendrait un analogue de la température de la Terre. Le flux d'eau correspondrait au flux de chaleur.
Attention aux malentendus possibles : la chaleur n'est pas un fluide !
Conclusion
Nous avons vu comment montrer expérimentalement opacité et transparence au rayonnement visible et infrarouge, ainsi que réflexion et absorption avec deux manipulations simples. Nous avons pu faire émerger la notion d'équilibre thermique radiatif.
Nous nous sommes servi de cette analogie pour étudier l'atmosphère terrestre et ses propriétés radiatives (transparence et opacité, due aux GES).
Nous avons construit un bilan radiatif simplifié de la Terre avec une atmosphère réaliste au premier ordre pour son opacité et sa transparence, mais isotherme.
Nous avons vu la différence avec la véritable atmosphère, au gradient de température décroissant avec l'altitude (atmosphère non isotherme).
Nous avons pu, avec ce modèle, mettre en évidence sur le spectre terrestre (et le bilan radiatif) la conséquence d'une augmentation de GES dans l'atmosphère : un réchauffement de la surface à flux solaire reçu constant.
Annexes - Spectre moyen d'émission de la Terre, issu d'observations disparates
Les spectres d'émission de la Terre montrent des disparités spatiales sur l'ensemble du globe.
Spectres d'émission en des lieux d'observation différents
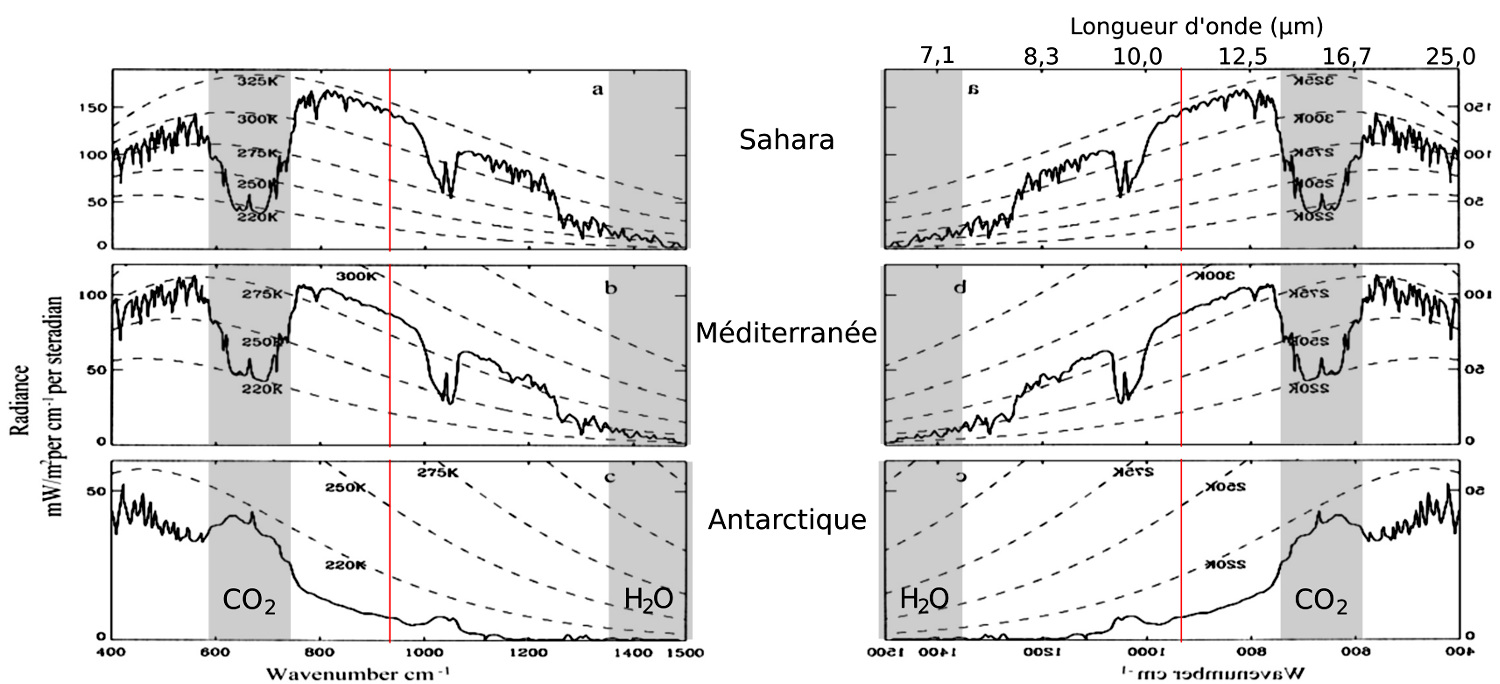
Sur la figure 27, les 3 spectres correspondent respectivement aux mesures au-dessus (a) du Sahara, (b) de la Méditerranée, et (c) de l'Antarctique. L'échelle des abscisses est en nombre d'onde (inverse de la longueur d'onde).
Les 3 spectres “bruts” sont ”inversés” (à droite) pour présenter les longueurs d'ondes dans l'ordre croissant (de 6,7 à 25 μm) et ainsi être plus proches des spectres vus précédemment. Les bandes d'absorption du CO2 et d'H2O ont été ajoutées ainsi que le canal d'observation à 10,8 μm (trait rouge, émission du sol).
On remarque que si les spectres ont un aspect général proche du spectre moyen avec des “creux” caractéristiques des bandes d'absorption des gaz à effet de serre, les pics et creux divers ne correspondent pas partout aux mêmes températures de spectres théoriques de corps noirs. Ainsi, à 10,8 μm lors des observations, le sol saharien était proche de 320 K (47°C), alors que la température de surface était voisine de 285 K (12°C) en Méditerranée et de 213 K (−60°C) en Antarctique. Ce sont de telles mesures répétées en divers lieux sur Terre et à différentes dates qui permettent d'obtenir et de reconstituer un spectre d'émission terrestre moyen qui correspondrait à une Terre de température de surface homogène et constante tout au long de l'année.
Figure 27. Spectres d'émission de la Terre mesurés par le satellite Nimbus 4, interprétés et "inversés"
G. Florides, P. Christodoulides, V. Messaritis, 2010. 3. Global Warming: CO2 vs Sun, in Global Warming, S.A. Harris (Ed.), IntechOpen, 250p. ISBN: 978-953-307-149-7
Images de la Terre selon divers canaux d'observation spectrale
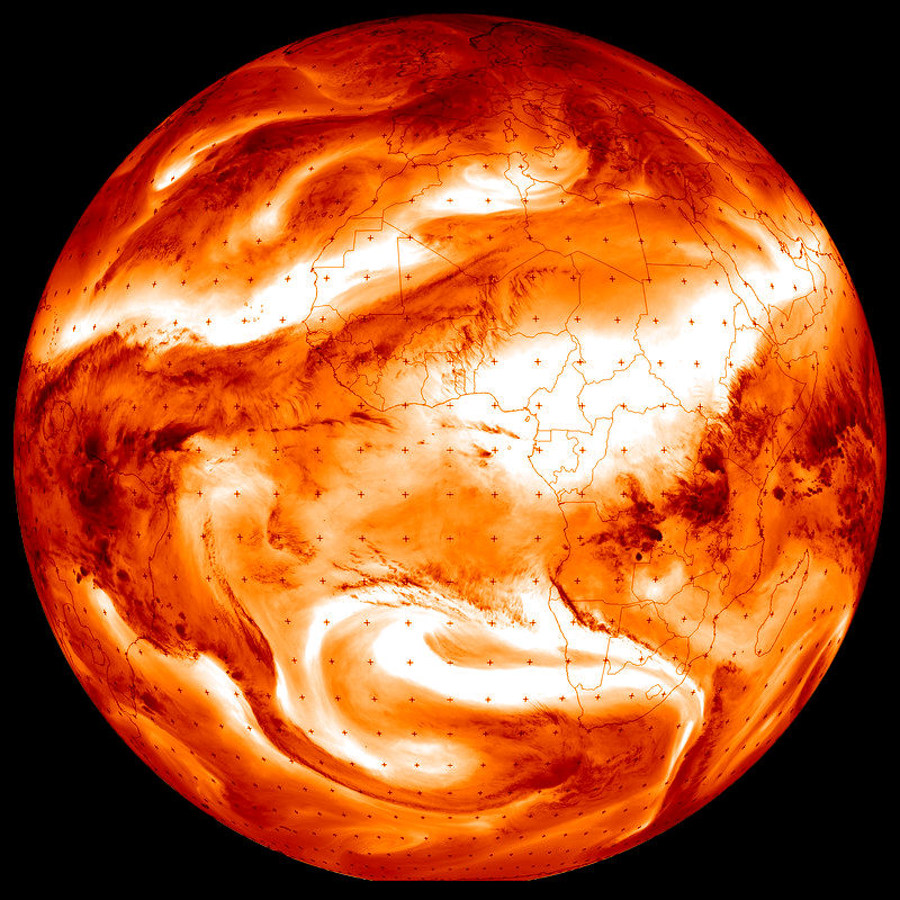
Les figures 28 et 29 présentent des observations réalisées par le satellite Météosat du 27 janvier 2020, images “centrées” sur le méridien 0°. L'intensité d'émission thermique est rendue par un dégradé en “niveaux de rouge” partant du noir pour l'absence de signal (absorption, diffusion), puis allant du rouge foncé pour le “ très froid”, au rouge de plus en plus clair plus il fait “chaud” pour arriver au blanc pour un signal très intense (signal maximum “ très chaud”).
Sur cette image on voit la surface de la Terre sauf là où il y a des nuages (présence d'eau liquide et solide – glace). On repère les limites des continents dont la température se distingue de celle des océans (température plus stable, moins variable au cours de l'année). | On voit les masses d'air humides. Plus il y a d'humidité (vapeur d'eau) et plus l'air est “opaque” jusqu'à une altitude plus élevée, où il est plus froid, et réémet donc moins d'IR (d'où une teinte plus sombre). Un air sec est “transparent” et donc très clair, voire blanc. La température “déduite” de l'émission de la vapeur d'eau n'indique pas celle du sol mais celle de l'altitude maximale des “masses humides” (la plus proche du satellite) dépendant de la quantité de vapeur d'eau. |
Revenons un instant à la seconde expérience avec la caméra thermique. L'observation du canal à 10,8 μm correspond à une observation directe de la tasse (pas d'obstacle aux infrarouges) : la couleur / température dépend alors de la température de la tasse. L'observation à 6,2 μm correspond, elle, à l'observation de la tasse à travers la plaque de plexiglas (obstacle aux infrarouges directs) : la température observée est celle de la plaque réchauffée par la tasse et dépend donc de la température de la tasse mais aussi de la distance entre la tasse et la plaque, d'autant moins réchauffée qu'elle est loin de la tasse. Dans l'expérience filmée, à distance tasse-caméra fixe, plus la plaque sera éloignée de la tasse chaude, plus sa température d'équilibre sera basse.
Pour citer cet article :
Rayonnement, opacité et effet de serre, Patrick Thollot, Olivier Dequincey, juin 2021. CultureSciences Physique - ISSN 2554-876X, https://culturesciencesphysique.ens-lyon.fr/ressource/rayonnement-modele-effet-de-serre.xml