Activer le mode zen
Ressource au format PDF
Classification
Numérisation d'un signal acoustique : effet de la fréquence d'échantillonnage (partie 2)
20/11/2013
Résumé
Cet article permet d'illustrer de manière sonore le principe de la numérisation d'un signal acoustique lors de l'étape de l'échantillonnage.
Le premier article décrivait les effets de la quantification sur ces mêmes signaux audio.
Cet article appartient aux dossier « Traitement du signal ».
Table des matières
1. Quelques rappels sur les étapes de la numérisation d'un signal
La numérisation consiste à transformer un signal analogique continu qui contient une quantité infinie d'amplitudes en un signal discret contenant une quantité finie de valeurs.
Le passage de l'analogique au numérique repose sur trois étapes successives : l'échantillonnage, la quantification, et le codage.
Dans le premier article, on a étudié l'étape de quantification, c'est-à-dire quels effets sont introduits par les différents choix de pas de quantification sur un signal donné. Dans ce deuxième article on étudie le choix de la fréquence d'échantillonnage.
Pour faire le point sur les étapes et la réalisation de la numérisation d'un signal, on pourra revoir les ressources suivantes :
- De l'intérêt de passer dans le monde numérique.
- Principe du passage de l'analogique au numérique.
- Comment convertir un signal analogique en signal numérique au laboratoire.
- Le traitement du signal et des images en 3 questions à Pierre Borgnat.
- D'autres ressources du dossier « Traitement du signal ».
On numérise ici un signal audio, ce qui permet de nous donner, en plus, une illustration sonore du choix de la fréquence d'échantillonnage.
2. Echantillonnage d'un signal acoustique : application à une seule fréquence, utilisation d'un signal sinusoïdal
Dans un premier temps, nous allons nous intéresser à un signal sinusoïdal. Ce signal a l'avantage de posséder un contenu spectral très simple (une raie), ce qui va permettre de mettre en valeur plus clairement les conditions nécessaires à une numérisation correcte.
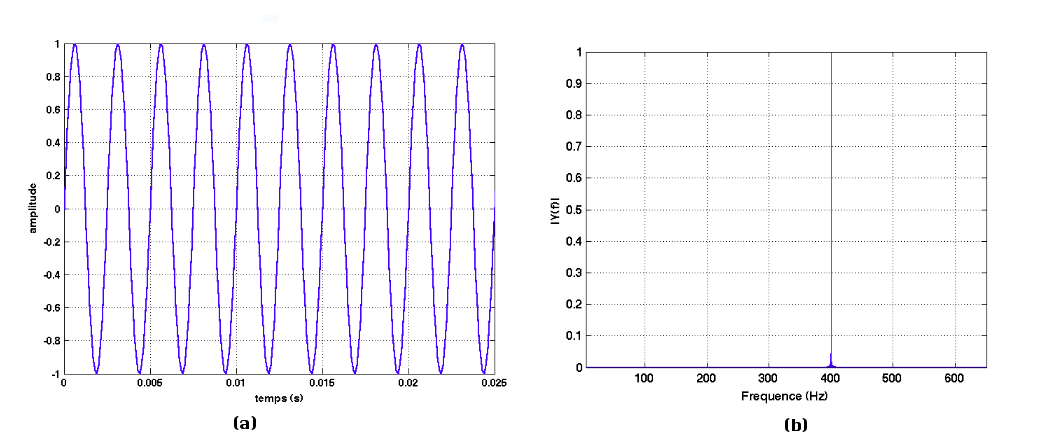
On travaille avec un signal sinusoïdal de fréquence 400 Hz, soit S(t) = sin (2 π f t), où f =400 Hz. La figure 1 donne en (a) la représentation temporelle et en (b) la représentation dans l'espace fréquentiel de S(t).
Figure 1. Représentation temporelle et spectrale d'un sinus de fréquence 400 Hz (a) signal temporel de S(t), (b) spectre de S(t). |
Il en résulte le signal sonore ci-dessous :
Source - © 2013 D. Chareyron
On va maintenant échantillonner ce signal.
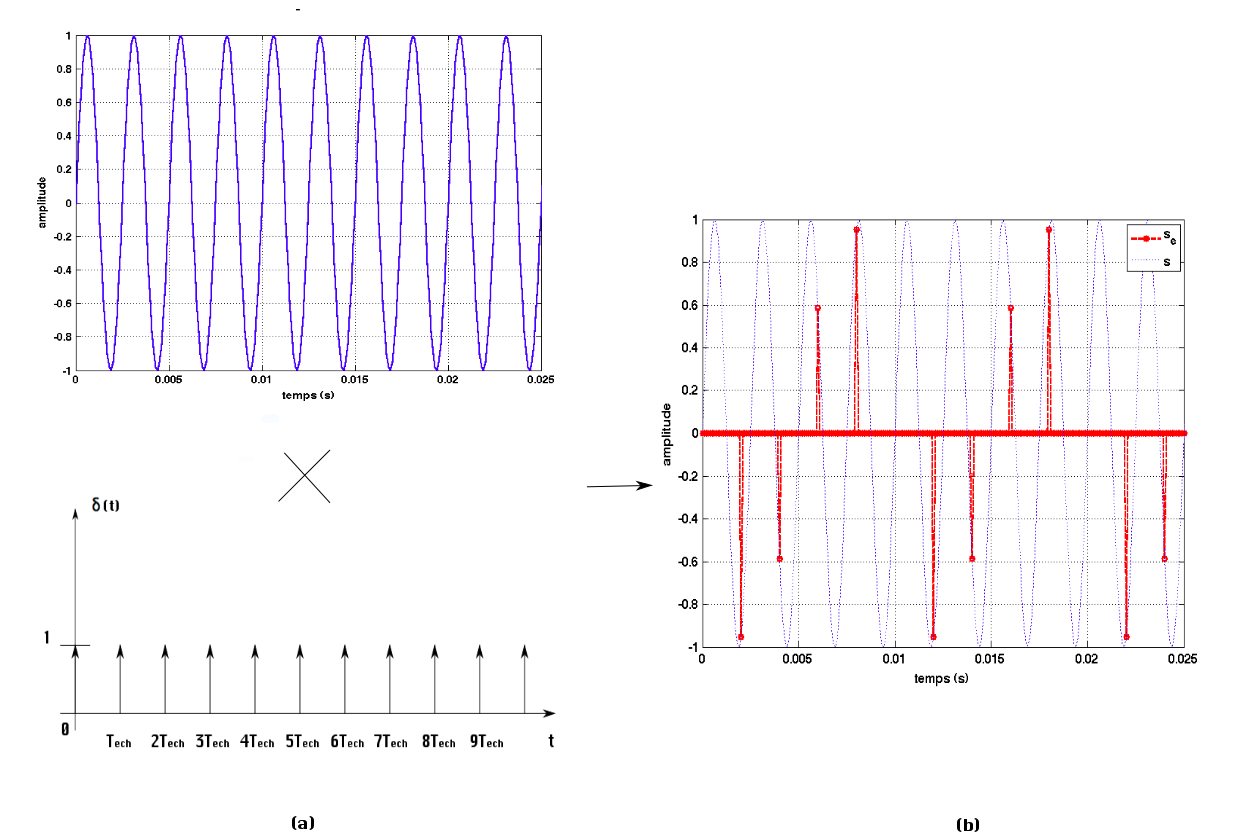
Echantillonner un signal revient à prendre un certain nombre de points régulièrement espacés de ce signal. Cette fonction consiste mathématiquement à multiplier le signal original S(t) avec un signal d'amplitude 1 à chaque instant pour lequel on prend un échantillon (opération répétée à la période Tech) et d'amplitude zéro sinon. Cette fonction est appelée peigne (ou train périodique d'impulsions) de Dirac δ(t), voir figure 2 (a) en bas.
Dans un premier temps, on échantillonne le signal sinusoïdal à une fréquence de 500 Hz. Dans tout le document nous appellerons S le signal original et Se le signal échantillonné.
La figure 2 (b) présente, en rouge, le signal temporel échantillonné Se.
Figure 2. Échantillonnage d'un sinus à la fréquence Fech = 500 Hz (a) signal sinusoïdal (haut) et train d'impulsion (bas), (b) signal sinusoïdal échantillonné à Fech = 500 Hz (en rouge). |
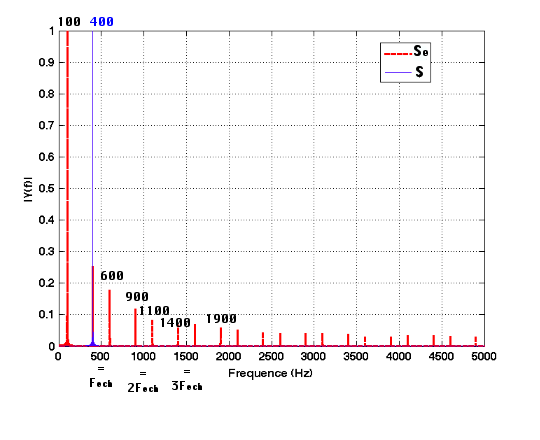
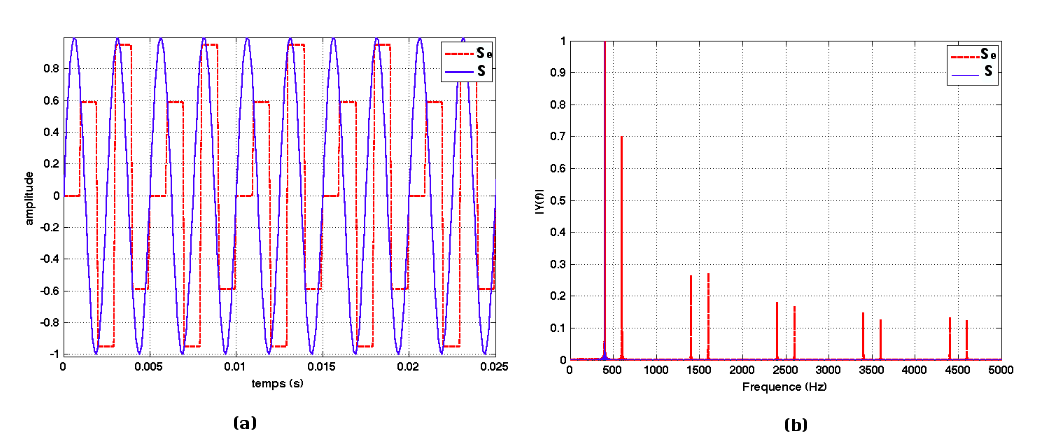
Le spectre du signal échantillonné est représenté sur la figure 3. On représente en bleu, la raie à 400 Hz du signal original S, et en rouge apparaissent les raies appartenant au signal échantillonné Se.
On constate que les deux signaux n'ont plus du tout le même contenu spectral.
Figure 3. Spectres des signaux S et Se avec Fech = 500 Hz Spectre du signal temporel original S ( en bleu) et échantillonné Se (rouge). |
Dans le spectre de Se, on voit apparaître une raie à 100 Hz, donc en-dessous du fondamental de 400 Hz, ainsi que des harmoniques.
Si on écoute le nouveau signal Se en audio, on constate, en effet, qu'il n'est plus fidèle au signal S :
Source - © 2013 D. Chareyron
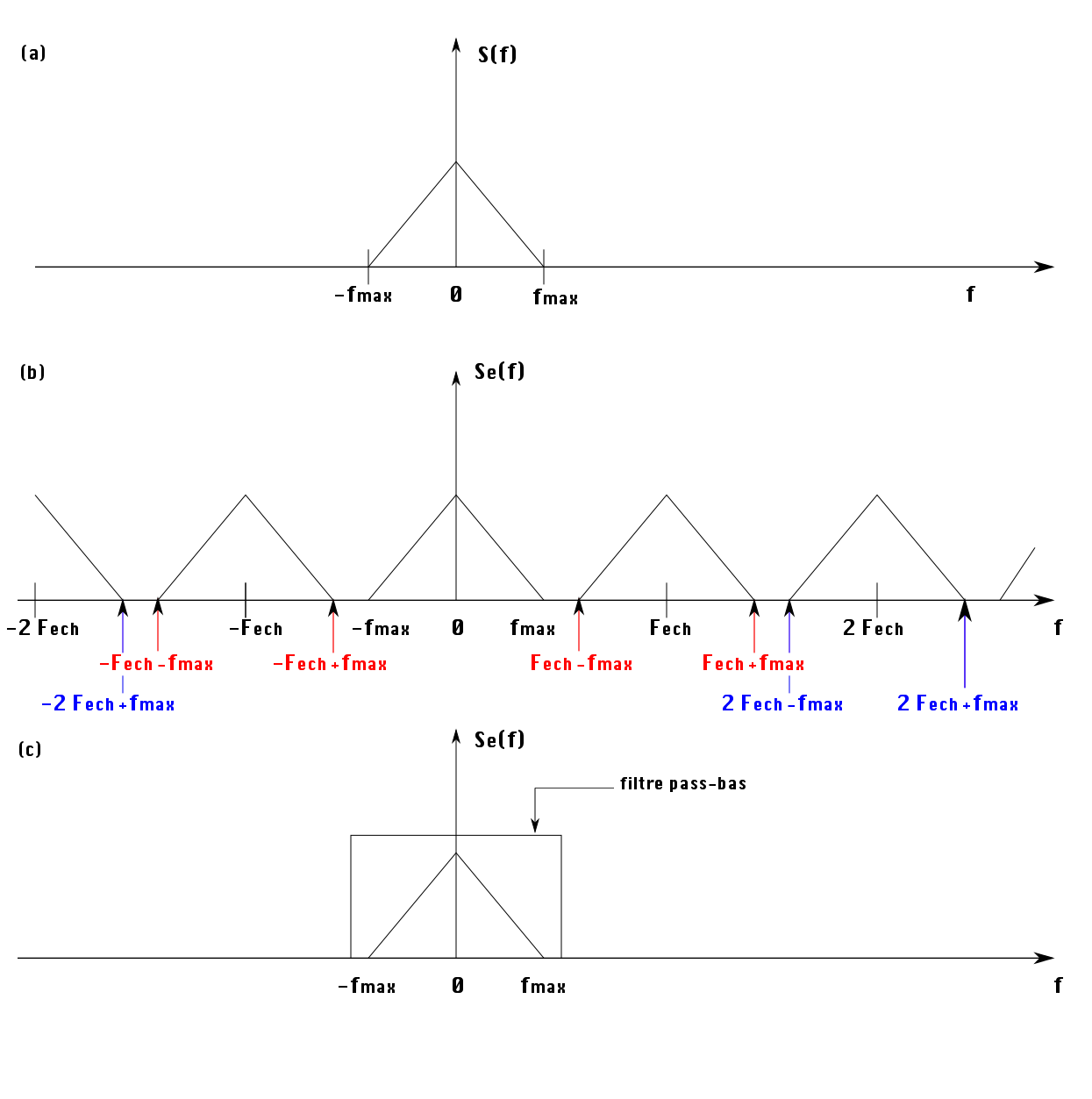
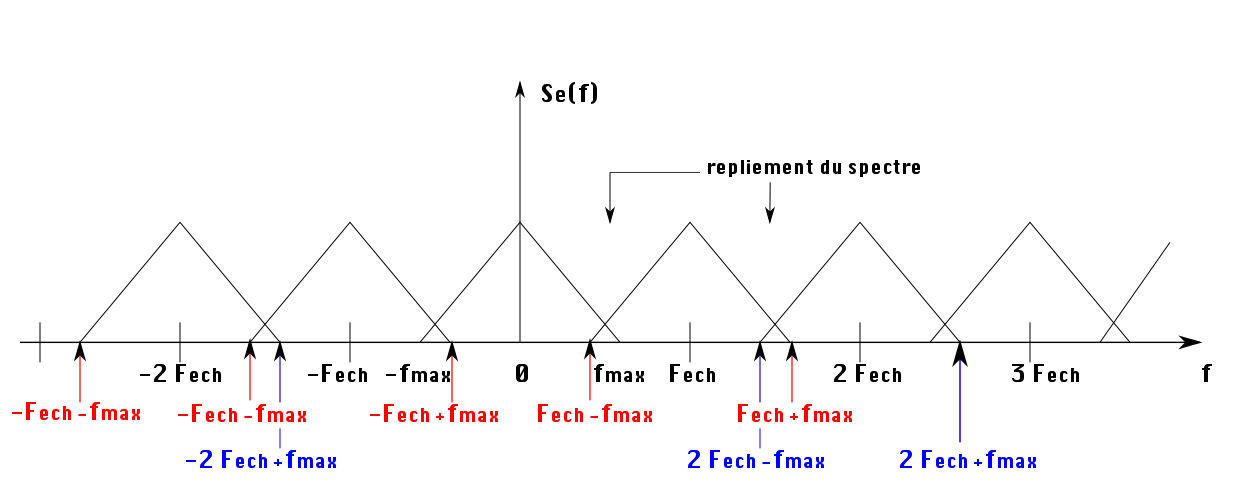
La figure 4 va nous aider à comprendre la modification du spectre du signal. Sur la figure 4(a) est représenté le spectre d'un signal quelconque. Le contenu spectral de ce signal est limité à fmax.
On va maintenant échantillonner, dans le temps, le signal correspondant à ce spectre. L'échantillonnage dans le domaine temporel agit comme une périodisation du spectre, et on va retrouver, espacé à la fréquence Fech, le contenu fréquentiel du signal original, figure 4(b).
Ainsi pour retrouver le signal original, il suffit d'utiliser un filtre passe bas, dont la fréquence de coupure est choisie entre fmax et Fech-fmax, figure 4(c).
Par contre, si la fréquence d'échantillonnage est mal choisie, il n'est pas possible de retrouver le signal original. La figure 5 montre un cas où on voit apparaître un repliement du spectre qui vient empêcher de retrouver l'information spectrale contenue dans le signal original.
Figure 5. spectre du signal échantillonné |
Il existe un critère, donné par le théorème de l'echantillonnage, qui permet de préserver l'information contenue dans le signal lors de sa discrétisation.
Théorème de l'échantillonnage - (Claude Shannon, 1948)
Si un signal continu S(t) ne contient aucune composante de fréquence supérieure à fmax, toute l'information concernant S(t) est entièrement contenue dans les valeurs du signal discret S(nTech), pourvu que Tech < 1/(2fmax). Tech correspond à la période d'échantillonnage. Avec Tech = 1 / Fech
Ainsi on trouvait avec le sinus des raies aux fréquences :
- 100Hz et 900Hz correspondant à Fech - fmax = 500 Hz - 400 Hz et Fech + fmax = 500 Hz + 400 Hz.
- 600Hz et 1400Hz correspondant à 2Fech - fmax = 1000 Hz - 400 Hz et 2Fech + fmax = 1000 Hz + 400 Hz.
- etc.
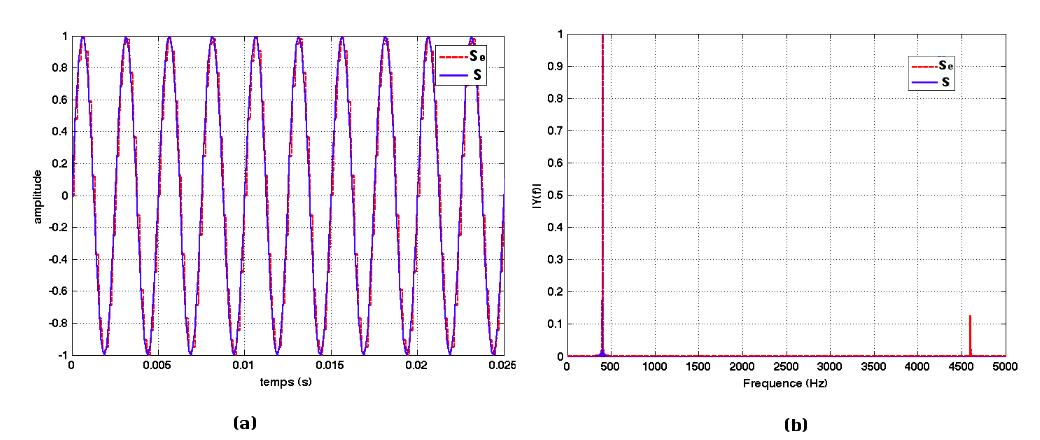
On va maintenant échantillonner le signal sinusoïdal à une fréquence de 1 000 Hz. Ce choix répond au théorème de Shannon, ainsi on s'attend à pouvoir retrouver le sinus à 400 Hz. Le résultat est donné dans la figure 6.
Figure 6. Signal sinusoïdal échantillonné à Fech = 1 000 Hz (a) signal temporel original S (bleu) et échantillonné Se (rouge), (b) spectres correspondants. |
Au regard du spectre, figure 6(b), on constate qu'aucune sous-fréquence n'a été introduite n'appartenant pas au signal original. Le signal échantillonné possède des harmoniques dûes à la périodisation du spectre, que l'on pourra couper à l'aide d'un filtre passe-bas.
En utilisant un peigne de Dirac, nous nous sommes placés tout-à-l'heure, dans un situation idéale. En pratique, on utilise un circuit échantillonneur bloqueur, qui garde la dernière valeur mémorisée durant la durée Tech (figure 6(a)).
Le résultat en audio (avant de lui appliquer un filtrage passe-bas) :
Source - © 2013 D. Chareyron
Dans la pratique on utilise plutot Fech > 10 Fmax. Cela permet en outre d'utiliser un filtre passe-bas d'ordre moins élevé.
Pour une fréquence d'échantillonnage à 5 000 Hz, le signal et le spectre sont présentés dans la figure 7.
Figure 7. Signal sinusoïdal échantillonné à Fech = 5 000 Hz (a) signal temporel original S (bleu) et échantillonné Se (rouge), (b) spectres correspondants. |
Le résultat en audio (avant de lui appliquer un filtrage passe-bas) ::
Source - © 2013 D. Chareyron
On entend très bien les deux fréquences du spectre.
3. Application à d'autres signaux
3.1 Une mélodie jouée au ukulele
Après ces explications, simples et visuelles car on étudiait un spectre composé d'une seule raie, nous allons travailler avec un signal musical représentant une mélodie jouée au ukulele.
Source - © 2013 Stéphane Arbon (composition et interprétation)
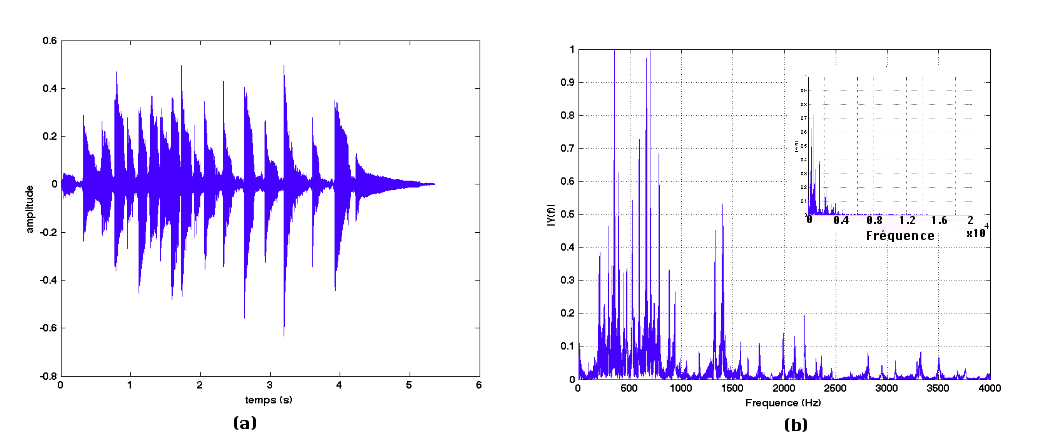
Sur la figure 8, on retrouve la représentation temporelle et spectrale de ce signal. Le spectre du signal jusqu'à 20 kHz est présenté en miniature en insert sur les fréquences de 0 à 4 kHz.
Figure 8. Signal d'une mélodie jouée au ukulele
(a) représentation temporelle, (b) représentation spectrale.
Dans cette application le spectre est plus riche que lorsqu'il s'agissait d'un sinus pur. Il comporte beaucoup plus d'harmoniques.
Il va donc falloir faire intervenir des paramètres qui vont décider de la bande passante, de la fréquence maximale de ce spectre. On pourrait choisir différents critères, comme la puissance d'une harmonique à partir de laquelle le signal est trop faible pour chercher à transmettre cette information.
Un autre critère repose sur la bande passante de l'oreille, généralement, on dit que l'on entend entre 20 Hz et 20 kHz. On ne va donc chercher à transmettre les infromations que dans cette gamme là. C'est pour cette raison que les disques audio sont généralement échantillonnées à 44100 Hz.
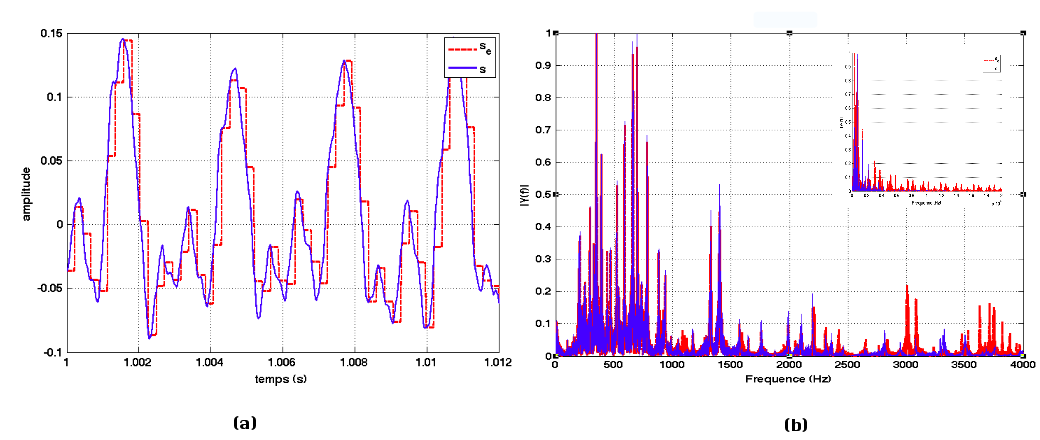
Dans un premier temps, pour se rendre compte de l'effet sonore que produisent la présence des harmoniques dans un signal, on décide que les harmoniques au-delà de 2 000 Hz, n'ont pas assez d'énergie pour être prises en compte. Ainsi, on va échantillonner le signal à la fréquence Fech = 4 410 Hz, figure 9.
Figure 9. Mélodie échantillonnée à Fech = 4 410 Hz (a) signal temporel original S (bleu) et échantillonné Se (rouge), (b) spectres correspondants. |
Le résultat en audio:
Source - © 2013 Stéphane Arbon (composition et interprétation)
L'oreille rend tout de suite compte de la dégradation du signal. La présence des harmoniques coupées ici reflète la richesse du son.
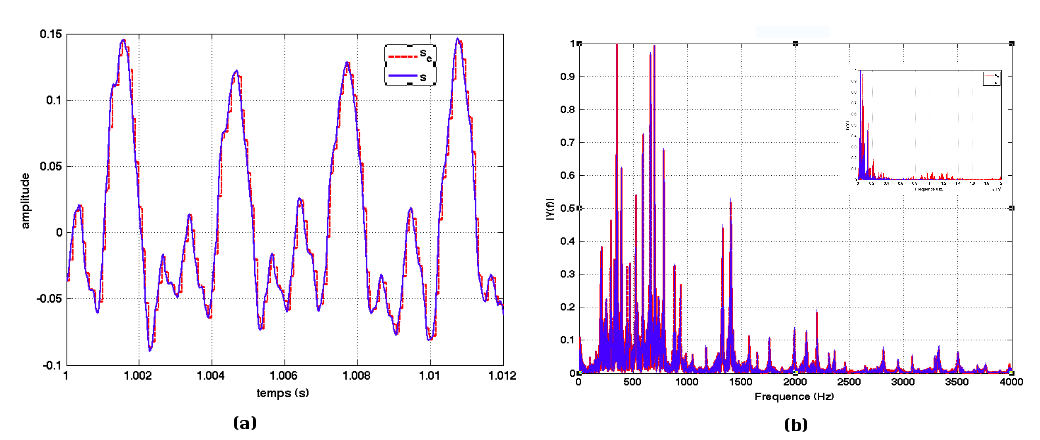
On choisit maintennant Fech = 11 025 Hz, on garde ainsi toutes les harmoniques jusqu'à 5 512 Hz, figure 10.
Figure 10. Signal sinusoïdal échantillonné à Fech = 11 025 Hz (a) signal temporel original S (bleu) et échantillonné Se (rouge), (b) spectres correspondants. |
Le résultat en audio:
Source - © 2013 Stéphane Arbon (composition et interprétation)
Le signal reste dégradé par rapport au signal original.
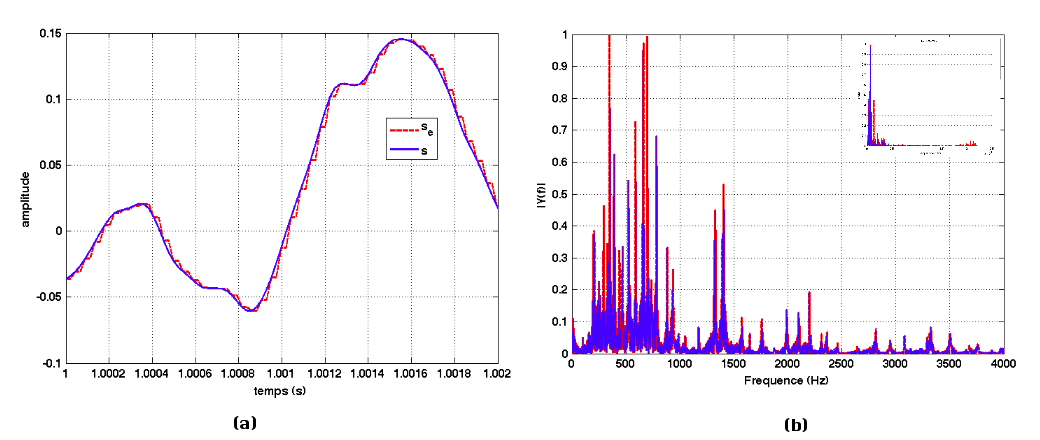
Avec Fech = 22 050 Hz, on va garder toutes les harmoniques jusqu'à 11 025 Hz, figure11.
Figure 11. Signal sinusoïdal échantillonné à Fech = 22 050 Hz (a) signal temporel original S (bleu) et échantillonné Se (rouge), (b) spectres correspondants. |
Le résultat en audio:
Source - © 2013 Stéphane Arbon (composition et interprétation)
On est maintenant très proche du signal original, numérisé à 44,100 kHz.
Dans la pratique,en studio la fréquence d'échantillonnage peut monter jusqu'à 96 kHz. Et il est légitime de se poser la question « si on n'entend pas, est-ce qu'on ne perçoit pas ? »
3.2 Un extrait de chanson
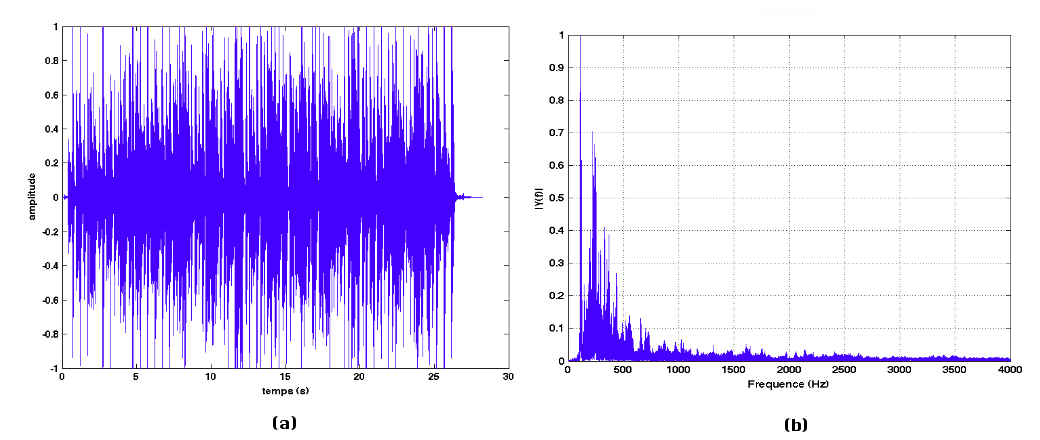
Dans ce deuxième exemple, le signal audio est une voix accompagnée à la guitare.
Source - © 2013 Stéphane Arbon (interprétation) - Christophe Bardon (composition)
Avec une fréquence d'échantillonnage Fech = 4 410 Hz, le résultat en audio :
Source - © 2013 Stéphane Arbon (interprétation) - Christophe Bardon (composition)
Avec une fréquence d'échantillonnage Fech = 11 025 Hz, le résultat en audio :
Source - © 2013 Stéphane Arbon (interprétation) - Christophe Bardon (composition)
Avec une fréquence d'échantillonnage Fech = 22 050 Hz, le résultat en audio :
Source - © 2013 Stéphane Arbon (interprétation) - Christophe Bardon (composition)
Pour donner encore un chiffre, on retiendra que la fréquence d'échantillonnage de la voix dans des applications de téléphonie numérique est de 8 kHz, le spectre de la voix étant généralement compris entre 300 et 3400 Hz.
Dans cet article nous n'avons pas parlé des limitations en amont et en aval de la chaîne d'un signal numérisé. Elles sont introduites notamment par la bande passante du microphone et des haut-parleurs, et vont alors venir modifier le contenu spectral du signal original.
Retrouver le premier article, sur les effets de la quantification sur ces mêmes signaux acoustiques.
Pour citer cet article :
Numérisation d'un signal acoustique : effet de la fréquence d'échantillonnage (partie 2), Delphine Chareyron, novembre 2013. CultureSciences Physique - ISSN 2554-876X, https://culturesciencesphysique.ens-lyon.fr/ressource/numerisation-acoustique-Chareyron2.xml