Activer le mode zen
Ressource au format PDF
Classification
Traitement du signal et des images : description et applications en 3 questions à Pierre Borgnat.
17/04/2013
Résumé
Cet article présente les outils et applications du traitement du signal et des images.
Cet article appartient aux dossiers : " 3 Questions à ..." et " Traitement du signal"
Table des matières
Pierre Borgnat est chercheur CNRS au « Laboratoire de Physique », à l'Ecole Normale Supérieure de Lyon.
Il travaille en particulier sur le traitement des signaux issus de la physique et des réseaux.
Page personnelle :« Pierre Borgnat »
1. Quel panorama peut-on dresser de la thématique : traitement du signal et des images ?
Historique
Cette thématique est née pendant la seconde guerre mondiale, dans les années 1940-1950, de la rencontre de la communauté de l'ingénierie électrique et électroniciens avec des mathématiciens. Les motivations en jeu étaient d’abord très générales et concernaient des problèmes de détection (radar, sonar) et de téléphonie. D'un côté les électroniciens fabriquaient les instruments de mesure et de l'autre les mathématiciens amenaient des outils de type transformée de Fourier ou processus aléatoires pour étudier les signaux en question.
Petit à petit le traitement du signal et des images est devenu une discipline à part entière, à la croisée de :
- l’électronique,
- l’automatique,
- l’ingénierie de manière générale,
- des sciences-physiques, grâce notamment à l'apport des méthodologies utilisées dans les sciences-physiques qui seront reprises en traitement du signal,
- des mathématiques appliquées,
- des statistiques,
- et de l’informatique utilisée pour déployer les méthodes.
Définition ce que l’on appelle traitement du signal et des images
Cela correspond à toutes les méthodes qui essaient d’extraire de l’information à partir d’une observation ou d’une mesure enregistrée. Cela peut être un signal, c’est-à-dire une mesure au cours du temps, ou alors une image, capture 2D ou 3D d’une observation.
Les observations dans le temps ou dans l’espace, sont en général bruitées, déformées, ou alors l’information que l’on cherche n’est pas directement ce que l’on mesure mais est un paramètre de la mesure (une fréquence, une amplitude, une phase…). Le traitement du signal et des images englobe toutes les méthodes qui permettent de rechercher efficacement ces informations en les débruitant, en les reconstruisant, en les estimant.
Le traitement du signal et des images vise à la fois à étudier théoriquement ce que l’on peut faire à partir d'un signal (trouver des bornes d’estimation, des intervalles de confiance...) mais aussi ce que l'on peut faire pratiquement concernant les aspects informatiques et algorithmiques comme trouver des méthodes efficaces à implémenter que ce soit sur ordinateur maintenant ou par le passé à l'aide de l'électronique.
Parmi les travaux fondateurs, on peut citer celui de Claude Shannon sur la théorie mathématique de la communication datant de 1948 [1]. Dans cet article l'auteur pose les bases à la fois de la représentation des signaux numériques échantillonnés mais aussi des résultats importants pour comprendre à quelle vitesse on peut faire de la communication type téléphone. Ces résultats sont toujours une des bases de ce que l’on fait en téléphonie mobile. On peut aussi citer, dans la communauté française, les travaux de Blanc-Lapierre sur les signaux aléatoires, dans les années 1950. À partir de cette époque, des universitaires ont commencé à s'intéresser à ces problèmes, ce qui a donné naissance à une communauté en traitement du signal et des images en France assez active et classée quasiment deuxième dans le monde derrière les Etats-Unis.
[1] Claude E. Shannon, A Mathematical Theory of Communication, Bell System Technical Journal, vol. 27, p. 379-423 et 623-656, Juillet et octobre 1948.
Domaines d'application
Historiquement la première application en traitement du signal concernait la question de la prédiction. Cela consiste à observer dans le temps ce qui se passe pendant quelques échantillons d'un signal donné (10, 20, 100, selon la mémoire dont on dispose) pour chercher à prédire ce qui va se passer pour ce signal dans le futur. La prédiction peut, par exemple, être utilisée pour des problèmes de contrôle. On peut aussi citer l'exemple du filtrage de Kalman, qui consiste à suivre une prédiction linéaire dans le temps, utilisé dans la mission Apollo pour la navigation jusqu'à la lune.
Pour des applications plus modernes, beaucoup de travaux ont été réalisés en acoustique : traitement de la musique ou de la parole. On peut citer en exemple les situations où l’effet cocktail entre en jeu, c'est-à-dire lorsque plusieurs personnes sont en train de parler les unes autour des autres. Il est possible de disposer plusieurs micros en différents lieux d’une pièce qui vont enregistrer les signaux émis, et ainsi voir chaque discours avec des amplitudes un peu différentes. Une question importante est de réaliser ce qui s’appelle la séparation de source, c’est-à-dire être capable de re-isoler chaque personne en train de parler. La séparation de source peut aussi être appliquée à un orchestre afin de séparer la contribution de chaque instrument. Ces méthodes ont données lieu depuis les années 1980 à énormément de travaux.
Une autre application récente importante concerne le domaine des télécommunications. L’explosion du téléphone portable ou de l’Internet mobile a renouvelé les questions posées sur l'enregistrement d'un signal de parole, mais aussi sa compression, sa transmission efficace et condensée sur des ondes hertzienne afin de faire fonctionner tous les téléphones mobiles actuellement en service.
Dans la partie liée au traitement des images, un renouveau important a eu lieu à partir des années 1980 grâce à l'apparition des méthodes dites temps-échelle basées sur la transformation en ondelettes. Ce renouveau est dû à la rencontre entre des chercheurs du domaine de la géophysique et des mathématiciens. Ils se sont rendu compte que des méthodes proposées par le géophysicien Jean Morlet (inventeur du mot « ondelette ») pouvaient se formaliser, ce qui a donné lieu à une révolution numérique de représentations des signaux et des images liées à la transformée en ondelettes. Ces travaux ont aboutit notamment, dans les années 2000, à intégrer dans le format jpeg 2000 une partie de représentation en ondelettes pour la compression des images.
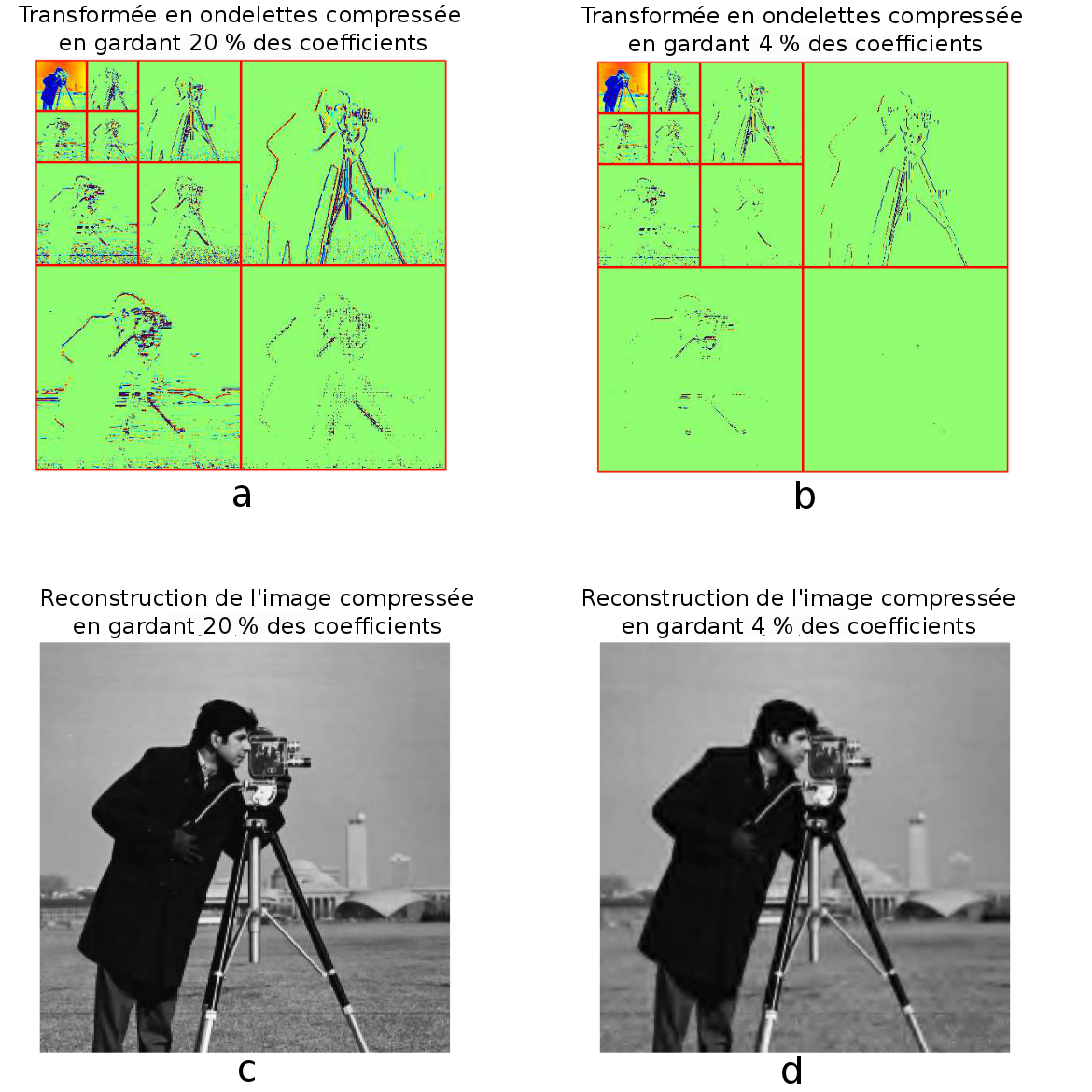
Le principe de la transformée en ondelettes et compression d'une image est présenté dans les figures 1 et 2.
L'utilisation de la transformée en ondelettes va permettre de représenter une image initiale, donnée dans la figure 1 - a, sous la forme d'une approximation et de détails, figure 1 - b.
Les approximations sont obtenues par convolution par une fonction d'échelle (un filtre passe-bas), et les détails ou coefficients d'ondelettes par convolution par la fonction d'ondelettes, puis en réduisant le nombre de points par deux. Le principe est d'itérer ce processus et de transformer l'approximation courante en une nouvelle approximation ayant 2 fois moins de points. Sur la figure 1- b le processus est présenté pour une seule itération, donc à l'échelle 1.
On effectue trois fois de suite l'itération, ainsi on passe d'une approximation de 512 x 512 pixels et 3 types de détails (horizontaux, verticaux et diagonaux) à une approximation de 64 x 64 pixels et toujours 3 niveaux de détails donnés par les coefficients d'ondelettes. Sur la figure 2 - a et - b, on note qu'il y a beaucoup de vert, qui code les coefficients aux valeurs proches de 0. L'image peut alors être compressée dans le domaine de la transformée en ondelettes en mettant à 0 rigoureusement les petits coefficients. La figure 2 - a représente la transformée en ondelettes compressée lorque l'on garde 20 % des coefficients avant de reconstruire l'image. La différence entre l'image reconstruite figure 2 - c et l'image initiale est quasi-invisible.
Dans la figure 2 - b on a gardé seulement 4 % des coefficients avant de reconstruire l'image et l'on peut voir figure 2 - d que des artéfacts commencent à apparaître.
Références:
- Ondes et ondelettes, Barbara Burke Hubbard. La saga d'un outil mathématique, 2000.
- A numerical Tour of Signal Processing, Gabriel Peyré.
Un dernier axe méthodologique partiellement lié aux ondelettes consiste à ne plus s’intéresser uniquement à des signaux qui sont stationnaires. Depuis les années 1970 les chercheurs se sont intéressés à des signaux qui évoluent dans le temps, entraînant un important développement de méthodes non-stationnaires qui permettent de suivre l'évolution dans le temps d’un signal. Typiquement, un discours est un signal acoustique non-stationnaire dans le temps qu’il faut modéliser par des méthodes spécifiques et en particuliers les méthodes de décomposition dites temps-fréquence.
2. Quels sont les outils du traitement du signal ?
Passage dans le domaine fréquentiel et Numérisation
Le premier outil pour le traitement d'un signal numérique ou analogique, vient de l’idée que l’on peut passer dans le domaine de Fourier (XIXème siècle), c’est-à-dire ne pas regarder uniquement ce qui se passe en temps ou en espace pour une image, mais regarder aussi quelles sont les fréquences qui sont présentes dans le signal ou dans l’image. Une bonne façon de réaliser la transformée de Fourier consiste à prendre en compte la taille d’une image ou la limite de durée d’observation d'un signal, et essayer d’estimer quelles fréquences sont présentes. Il est aussi possible de faire du filtrage pour éventuellement enlever des parties des composantes fréquentielles qui ne représentent que du bruit et donc pas l’information que l’on cherche à extraire. C’est le point de départ du traitement du signal et des images analogiques ou numériques.
Le deuxième outil permet d’aller vers ce que l’on fait actuellement quasiment exclusivement : le traitement numérique. Cela consiste à transformer un signal analogique en un signal numérique. La première étape est l’échantillonnage où l'on va prélever des points du signal, en nombre discret, comptable, de façon à pouvoir les mettre dans une mémoire d’ordinateur qui ne fonctionne que de manière discrète. La base de l’échantillonnage est justement décrite dans l’article de Shannon de 1948.
Théorème de l'échantillonnage
Fe ≥ 2 fmax. Le signal d’origine est bien représenté si les fréquences présentes dans ce signal sont inférieures ou égales à la moitié de la fréquence d’échantillonnage.
Un exemple bien connu concerne l’échantillonnage au cinéma. On sait que la vue est très peu sensible à plus de 24 images par seconde, ce choix pour la fréquence d’échantillonnage permet de dire que l’on a une assez bonne représentation de la séquence video.
La deuxième étape est la quantification du signal. Les échantillons ne doivent plus prendre des valeurs continues mais des valeurs discrètes qui soient compatibles avec des formats de stockage sur l’ordinateur (valeur binaire, format flottant...), c'est-à-dire un nombre fini de valeurs possibles. La combinaison de ces deux opérations (échantillonnage et quantification) permet, étant donné une mesure analogique que l’on suit dans le temps, de la transformer en un signal numérique. Le point important est que l’on a des résultats théoriques qui nous disent à quel point le signal numérisé représente bien le signal analogique initial.
Ces deux outils sont les principaux. Il y en a un troisième que je ne développerai pas ici et qui consiste en l’implémentation pratique de ces méthodes, c'est-à-dire comment réaliser pratiquement ces étapes. Actuellement la partie électronique permet de numériser les signaux et par la suite l’informatique va faire le calcul effectif de la transformée de Fourier.
Développements récents
Puis, dans les développement récents il y a tous les outils modernes de traitement du signal programmés sur ordinateur, en passant dans des langages de programmation divers comme le C, le Python, le matlab…
On peut citer :
- les méthodes temps-fréquence, qui permettent de trouver des représentations de l’évolution d’un spectre instantanné au cours du temps (figure 4).
- les méthodes temps-échelle, comme la transformée en ondelettes. Ces méthodes pemettent de représenter, pour un signal, non plus ses fréquences dans le temps mais l’échelle de chaque partie du signal au cours du temps (figure 2). Définir simplement l’échelle c’est définir la taille de la fenêtre dans laquelle on regarde le signal étudié. On va regarder le signal à une première échelle donnée, puis on va le regarder avec une résolution 2 fois moins grande, puis 4 fois moins grande, etc. Cela permet d’avoir des versions approchées du signal dans lequel on a gommé de plus en plus de détails.
- les méthodes d'invariance d'échelle, c’est-à-dire le fait qu’un objet observé à une échelle donnée ou observé à une échelle 10 ou 100 fois plus grande, garde les même propriétés en moyenne. C’est le cas typiquement lorsqu’on regarde des fractales en mathématiques, les vitesses des particules fluides en physique de la turbulence, ou dans le monde réel le chou romanesco.
- la résolution de problème inverse, qui a pu se développer grâce à l’avènement d’ordinateurs plus puissants dans les années 1980-1990. Il ne s'agit pas simplement d'inverser le problème direct mais de venir rajouter des éléments dans le modèle qui permettent de réduire le bruit, lisser la solution obtenue...
3. Quelles sont les applications du traitement du signal et des images ?
Exemple d'application des méthodes temps-fréquence
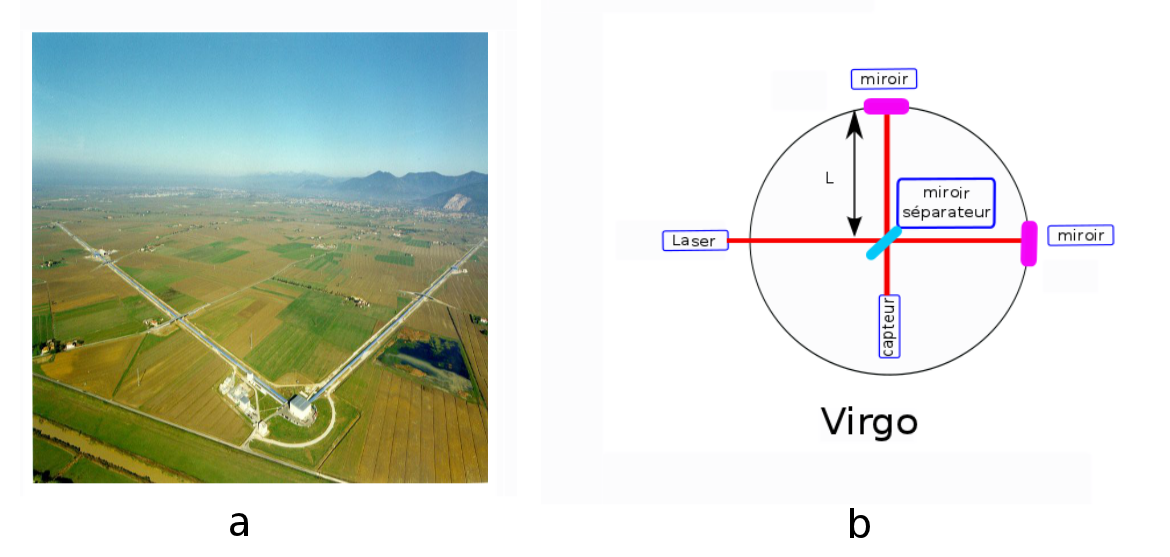
Des collègues de l'ENS de Lyon, chercheurs en traitement du signal, se sont investis dans des expériences qui visent à observer des ondes gravitationnelles (projet VIRGO en Italie, figure 3).
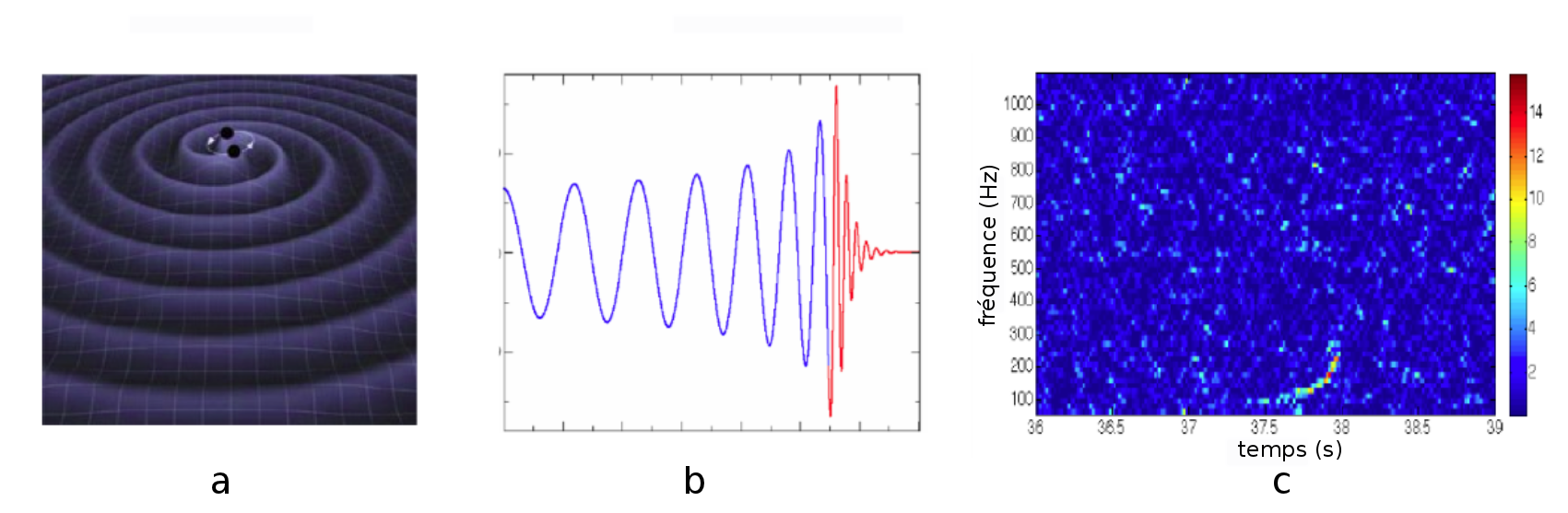
Ils se sont appuyés sur des méthodes temps-fréquence pour détecter la coalescence d’étoiles binaires. Les ondes gravitationnelles n'ont encore jamais été observées. Les prédictions théoriques, qui remontent à la théorie de la relativité générale d'Einstein, proposent que si deux étoiles tournent l’une autour de l’autre très rapidement dans la phase de coalescence (figure 4 - a), c’est à dire quand l’une va rentrer dans l’autre, le système, en tournant de plus en plus rapidement, va émettre une onde à une fréquence qui va augmenter dans le temps, figure 4 - b.
Ces signaux étant noyés dans du bruit, seule une approche de type temps-fréquence qui en donne une carte à deux variables (temps en abscisse, fréquence en ordonnée) permettrait de voir un excès d'énergie sur cette trajectoire de fréquence qui varie dans le temps, (ici entre 37,5 et 38 s) puisque certains points de l'image temps-fréquence sortent du bleu foncé, figure 4 - c.
Pour cette expérience ils utilisent l'interféromètre Virgo (figure 3), pour tenter de détecter une déformation de l’espace-temps produite par l’onde gravitationnelle qui emettra une fréquence croissante avec le temps. Le traitement du signal intervient ici pour le suivi dans le temps de fréquence instantanée dans un environnement très bruité.
Référence :E. Chassande-Mottin
Exemples d'applications des méthodes de résolution de problème inverse
Définition
Ce que l’on appelle problème direct, c’est à partir de la connaissance de la physique du modèle : sources et mileu donnés, on est alors capable de calculer partout dans le milieu ce qu’émettent ces sources. Dans le cas du problème inverse, étant donné les mesures en quelques points dans le milieu, comment être capable de retrouver le signal émis par les sources.
Du côté des images astronomiques, le traitement du signal intervient souvent dans le domaine de résolution de problèmes inverses. Les images astronomiques que l’on obtient sont en général dégradées. Si elles sont obtenues à terre elle sont dégradées à cause de la turbulence atmosphérique, des nuages ou d'un flou d’instrument, ce dernier défaut étant valable pour des images prises à Terre comme en l'air. Le télescope Hubble qui était myope est un cas connu.
Typiquement on s’appuie sur un modèle de formation de l’image en prenant en compte toutes ses dégradations possibles et le mouvement des étoiles pour essayer d’améliorer la précision de l’image obtenue. On cherche finalement à améliorer l’a priori sur l'image que l’on regarde sachant que l’on connaît déjà l'objet imagé. Ce sont des outils de traitement d’image ou de signal qui ont contribués à la détection d’exo-planètes.
En géophysique, l’étude des ondes sismiques a été une motivation importante historique du développement du traitement du signal et de l’étude de phénomènes aléatoires. Il y a encore beaucoup de travaux qui se font, que ce soit à des fins de prospection dans le sol, ou à des fins scientifiques de compréhension de la façon dont s’étage le manteau terrestre. Pour cela, on fait encore appel aux problèmes inverses. Des ondes sismiques sont émises soit par des campagnes de mesure, soit naturellement et on essaie d'extraire l’information pour répondre à la question : comment s’organise le sous-sol à partir de la propagation des ondes sismiques ?
Plus récemment, un dernier axe important d’applications est relatif aux images et signaux en médecine et en biologie.
Un scanner (rayon X ou IRM) est un appareil qui réalise une mesure appelée tomographie, qui consiste à représenter un corps humain à travers des coupes. Il donne accès à des profils de densité sur des sections prises à différents angles autour de la personne. Ensuite il faut reconstruire l’image. Réaliser une tomographie c’est encore une fois résoudre le problème inverse, et en particulier lorsque les images sont bruitées (la personne reste un temps court et défini dans le scanner, bruit de l'instrumentation, problèmes de recalage si la personne bouge un peu...)
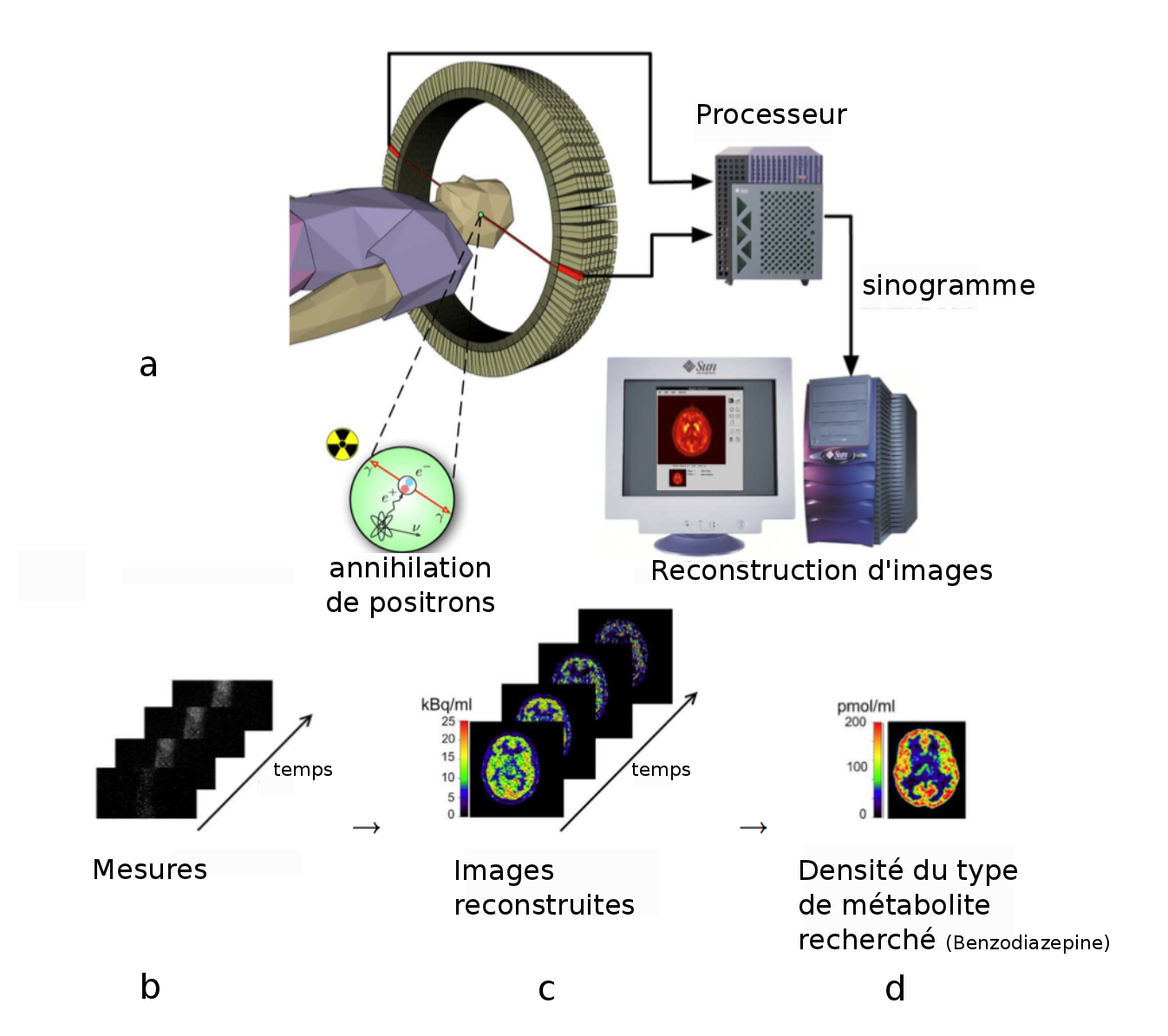
La figure 5 - a présente la technique de tomographie par émission de positrons. Les images sont obtenues en détectant les directions d'émission de photons créés par l'annihilation de positrons émis par un marqueur biologique. L'image mesurée est un sinogramme (figure 5 - b), indexé par les angles, et il faut reconstruire à chaque instant l'image 2D (ou 3D) réelle en résolvant le problème inverse de la tomographie, figure 5 - c. Finalement, la densité d'un type de métabolite dans l'organisme est obtenue en combinant les images au cours du temps, figure 5 - d.
Référence :Méthodes proximales pour la résolution
de problèmes inverses. Application à la Tomographie par Emission de
Positrons,Nelly Pustelnik. Thèse de doctorat en Sciences de
l'université Paris-Est, 2010.
En outre le traitement du signal permet aussi l'amélioration du contraste, de la résolution et le débruitage d’images de microscopie dans le domaine de la biologie.
Exemples d'application du traitement statistique des signaux
J’ai travaillé dans le domaine de la turbulence où l'on s'intéresse à l’évolution d’un fluide à grande vitesse. On va trouver une vitesse mesurée en un point qui est très erratique, très peu prédictible, aléatoire mais cet aléatoire se structure précisément avec des idées d’invariance d’échelles : des gros tourbillons qui se cassent en plus petits tourbillons etc. Et dans cet exemple-là le traitement statistique du signal intervient en particulier avec les outils de temps-échelle pour estimer les lois d’échelle sur les vitesses.
Le traitement statistique des signaux peut aussi être utilisé pour étudier des phénomènes de type marche aléatoire, comme un polymère soumis à des fluctuations de température.
Si on s’éloigne de la physique, un domaine actuel point de rencontre entre traitement du signal, informatique et traitement statistique, est l’étude des réseaux et graphes de terrain. On a de plus en plus de moyens pour mesurer des données relationnelles entre des gens ou des objets. On parle beaucoup du web social. Avec ces différentes communautés, il y a un point de convergence pour chercher à étudier des objets qui ne sont pas simplement décrits par des signaux dans le temps ou des images (en 2 ou 3D) mais qui sont des données relationnelles que l’on peut représenter par des graphes.
L'analyse de graphes de terrain est à la rencontre de nombreuses communautés : des chercheurs en algorithmique des réseaux, traitement statistique, physique statistique qui viennent avec leurs outils théoriques, des chercheurs en sciences humaines (sciences sociales en particulier) qui posent les bonnes questions sur les données, des experts pour enregistrer des données numériques tels que des informaticiens des réseaux et télécommunications. Cela renouvelle un champ interdisciplinaire qui permet d’appliquer ces outils vers des objets moins classiques.
Dans notre groupe nous avons réalisé un travail d’analyse statistique sur les communications par Internet. Dans les années 1990 suite à l’explosion des réseaux de communications entre ordinateurs et en particulier l’Internet et le web, le nombre de terminaux connectés s’est démultiplié. Les chercheurs du domaine se sont rendu compte que même si ce système est complètement artificiel car construit par l’homme, le nombre de terminaux connectés est tellement grand que les flux de communication ne peuvent plus être bien compris ni modélisés.
Par exemple, on se sait plus répondre à la question de la demande attendue en télécommunication à un instant t de la journée. Puisque l’on ne sait plus modéliser ces réseaux à cause de leur trop grande taille, le traitement statistique du signal intervient ici, en proposant de réaliser des mesures sur ces réseaux afin d'élaborer des modèles prédictifs. Certes ces modèles ne permettent pas de comprendre exactement ce que fait chaque personne sur le réseau, mais ils permettent efficacement d’obtenir des idées du type de trafic (dense, large), de détecter des anomalies sur le réseau, des intrusions, des pannes, ou encore des évènements inattendus (par exemple le phénomène de flash crowd). Et ce sont des choses qui impactent énormément les opérateurs de télécommunications.
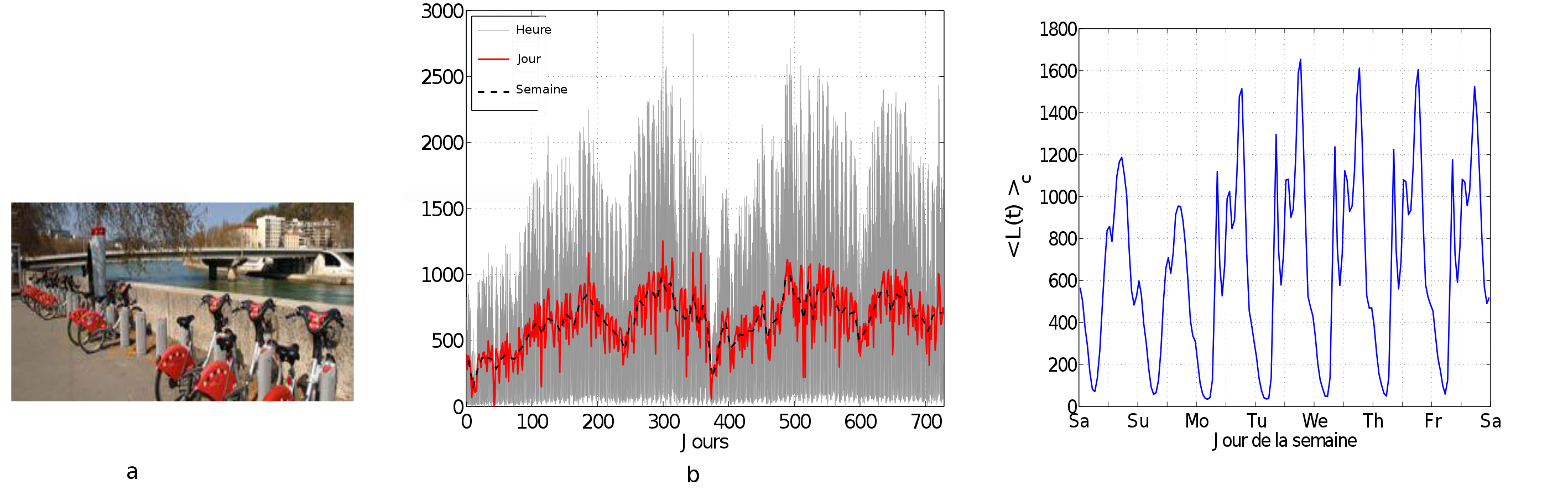
Une autre application plus récente est l’analyse des déplacements en Vélo’v, service de vélos de la ville de Lyon.
Depuis une petite dizaine d’années les chercheurs issus de sociologie, de l’étude des transports et de l'étude des données ont voulu reprendre les questions sur la mobilité des personnes à l'aide des traces numériques des déplacements.
Depuis 4-5 ans, à Lyon, un groupe de travail a été monté avec des collègues en sociologie, en géographie, en économie des transports et en informatique sur l’analyse des déplacements en Vélo’v, figure 6 - a. Après avoir rencontré le Grand Lyon et l’opérateur Cyclocity (JC Decaux), nous avons pu lancer des analyses sur les déplacements pour essayer de comprendre les rythmes dans l’espace et dans le temps de l’utilisation des Vélo’v.
La figure 6 - b présente l'évolution du nombre de locations horaires par heure (gris), jour (rouge) ou semaine (noir) sur les 2 premières années de fonctionnement du Vélo'v. De ce signal temporel on en déduit un modèle de profil moyen de locations horaires (figure 6 - c).
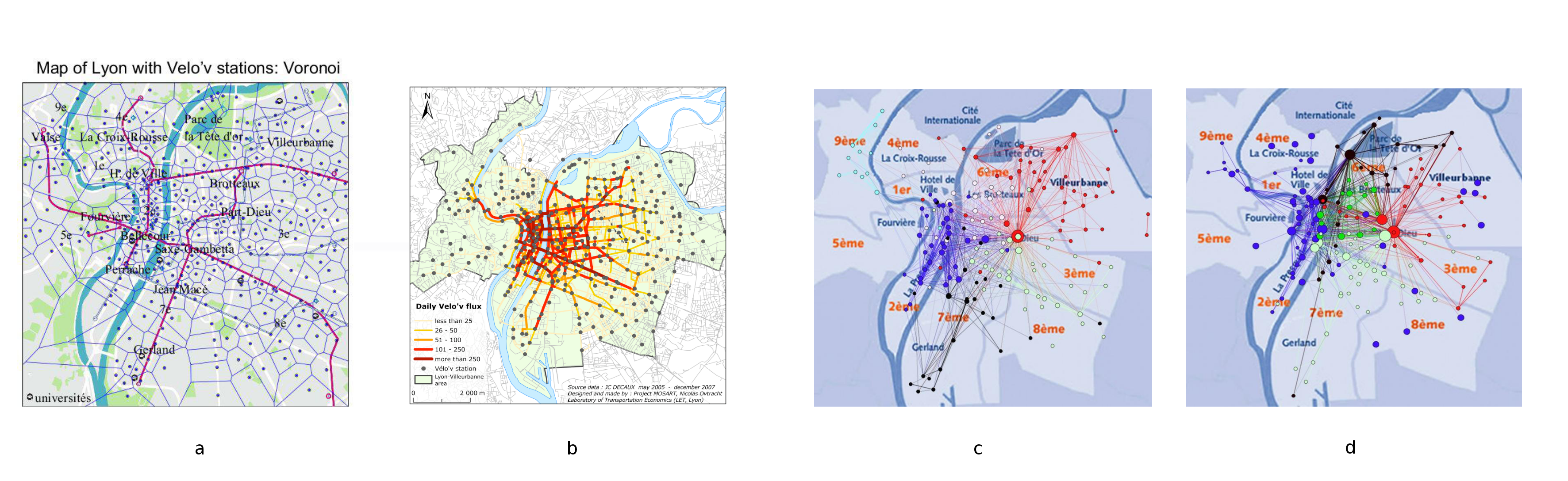
Les stations Vélo'v sont déployées uniformément dans l'espace de la ville (figure 7 - a).
On peut mener une étude spatiale et temporelle de la dynamique des mouvements en Vélo'v. Sur la figure 7 - b, on a inféré quels étaient les flux moyens de Vélo'v dans les différentes rues de Lyon. Sur les figures 7 c et d, on représente sous forme de réseau les connections entre stations Vélo'v les lundis matins (c) et samedi après-midi (d); les couleurs indiquent des groupes de stations voyant beaucoup de trajets en Vélo'v entre elles à ce moment de la semaine. On peut constater un mode d'utilisation différent le samedi, où par exemple apparaît un groupe des stations du Parc de la Tête d'Or qui connecte aussi toutes les stations suivant les berges du Rhône et celles près de l'Hôtel de Ville. Ces cartes sont obtenues en utilisant des outils d'analyses de réseaux dynamiques venues du traitement du signal.
La problématique est là-encore la même que dans l'exemple des communications sur Internet, ou pour l'étude des propriétés de la turbulence, c’est-à-dire que l’on a énormément de données qui arrivent à grande vitesse. Il n'est pas possible de regarder tous les détails. Il faut alors mettre en place des procédures systématiques automatisées qui vont permettre de réduire le bruit (ici les fluctuations) et de tenir compte des évènements extraordinaires : incidents sur le réseau de bus, de Tram ou de métro qui va se répercuter par une croissance du trafic des Vélo’v, comportement des usagers en vacances ou en période scolaire, incidence des jours de pluie ou de beau temps...
Il faut donc être capable de mettre en regard tous ces facteurs explicatifs et cela demande de faire du traitement statistique de signaux de grandes dimensions : imaginer tous les déplacements possibles de toutes les stations Vélo’v.
Un objectif scientifique est de comprendre comment les usagers se sont emparés du Vélo’v, pour quels usages et quels motifs de déplacement.
Le deuxième objectif qui est plutôt celui de l’opérateur et du grand Lyon est d’améliorer le fonctionnement du Vélo’v, c’est-à-dire être capable de répondre à une question du type : si on ouvre une nouvelle gare (comme la gare Jean Macé dernièrement), ou alors si un nouveau quartier se peuple un peu plus (comme celui des Confluences à Lyon), est-on est capable de trouver la meilleure façon de redéployer les bornes de vélos pour répondre aux nouvelles demandes.
Références:
- Modélisation statistique cyclique des locations Vélo'v à Lyon, Pierre Borgnat. 22e Colloque sur le Traitement du Signal et des Images. GRETSI-2009, Dijon.
- A dynamical Network View of Lyon's Vélo'v Shared Bicycle System, Pierre Borgnat, dans Dynamics of Time-Varying Networks (N. Ganguly et al.ed.), 2013.
- Characterizing the speed and paths of shared bicycle use in Lyon, Pablo Jensen et al., Transportation Research Part D, vol. 15, no 8, p.522-524, 2010.
Cette dernière application s'éloigne du traitement du signal traditionnel. On y retrouve cependant un trait commun : la prise en compte des évolutions et des dépendances dans le temps des signaux mesurés.
Pour citer cet article :
Traitement du signal et des images : description et applications en 3 questions à Pierre Borgnat, Pierre Borgnat, avril 2013. CultureSciences Physique - ISSN 2554-876X, https://culturesciencesphysique.ens-lyon.fr/ressource/signal-images-Borgnat.xml