Représentation spectrale d'un signal

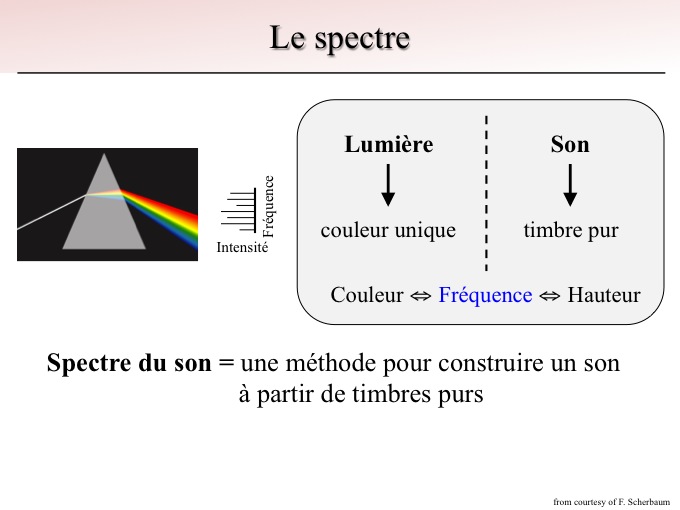
Pour comprendre le principe de la décomposition spectrale, le plus simple est de prendre comme exemple celui de la lumière. Lorsqu'on envoie une lumière blanche sur un prisme, elle se décompose en un spectre de différentes couleurs. La lumière blanche correspond ainsi à la somme de différentes longueurs d'onde ou couleurs (dans le visible) qui la composent. La longueur d'onde λ est reliée à la fréquence f par la relation : λ = c / f où c correspond à la célérité de l'onde.

Pour le son on peut faire une analogie parfaite. Un son peut se décomposer en une somme de fréquences pures. En acoustique cela s'appelle la hauteur du son. Elle ne correspond pas à son intensité mais à sa fréquence. Un son va être plus ou moins haut, on dit plus ou moins aigü.

On peut tracer le spectre d'un son, qui va être le strict analogue du spectre lumineux. Il s'agit alors de tracer l'intensité en fonction de la fréquence. Ainsi pour chaque fréquence on va regarder quelle intensité est présente dans une fréquence donnée. Tracer le spectre d'un signal acoustique va permettre d'avoir accès à l'information portée par ce son, c'est-à-dire connaître sa répartition de timbres purs.

Source - © 2012 V. Vidal

Figure 1. Analogie lumière / son pour comprendre la signification du spectre

Pour illustrer la superposition de timbres purs, on peut s'aider des instruments de musique.

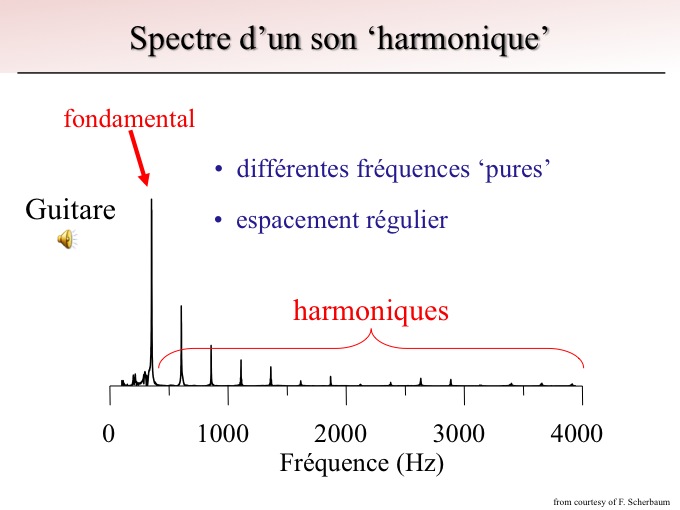
Si l'on trace le spectre du « do » de guitare, c'est-à dire l'intensité associée à chaque fréquence, on trouve un spectre bien marqué avec différentes fréquences pures qui ont un espacement régulier, figure 2. Dans ces fréquences on va pouvoir distinguer ce que l'on appelle la fréquence fondamentale, qui correspond au pic le plus à gauche, et les différents harmoniques qui correspondent aux pics de fréquences plus élevées.

Source - © 2012 V. Vidal

Figure 2. Décomposition spectrale d'un « do » de guitare

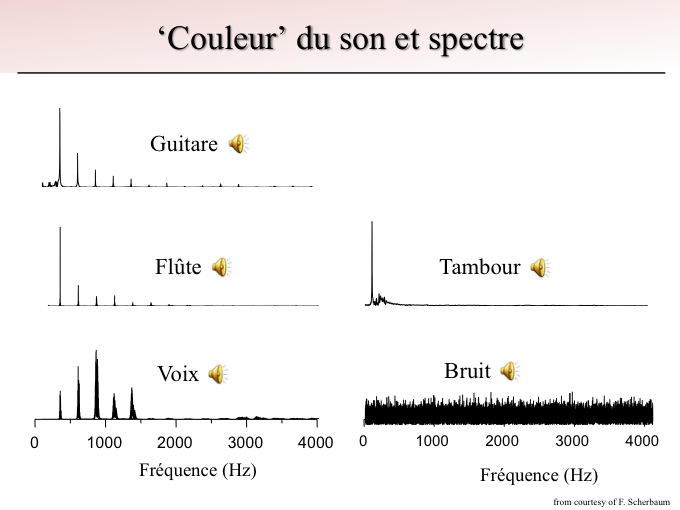
Sur la figure 3 sont représentés les spectres de plusieurs instruments de musique. Les spectres de gauche correspondent tous à la même note « do » interprétée par une guitare, une flûte et la voix. Cliquez sur le lecteur ci-dessous pour entendre ces 3 extraits.

Source - © 2012 V. Vidal

À gauche : la note "do", à droite : autres sons.

Figure 3. Décomposition spectrale

On écoute la même note mais le ressenti est différent, et cette information est traduite dans le spectre. La même note est jouée, c'est à dire que l'on va retrouver la même fréquence fondamentale et une répartition semblable des harmoniques dans le spectre, mais avec des différences d'amplitude dans les harmoniques.

Le spectre du tambour et du bruit blanc sont très différents (écoute ci-dessous). Dans le cas du bruit blanc aucune fréquence ne ressort particulièrement du spectre (par définition).

Ainsi le timbre du son correspond à la relative amplitude des harmoniques présentes dans le spectre.

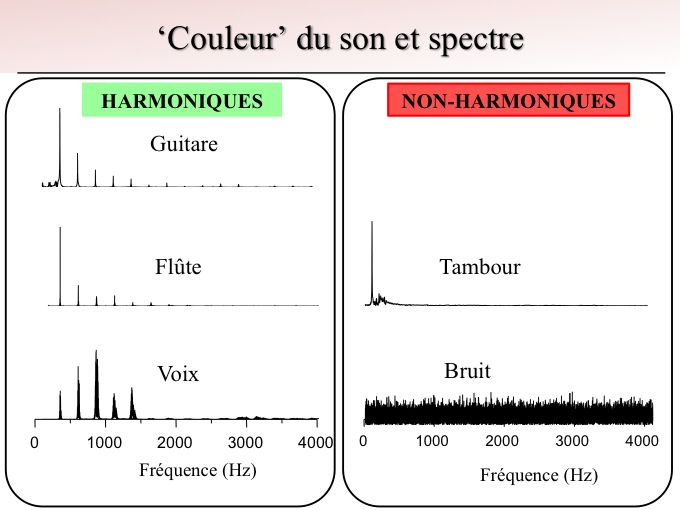
Les signaux dits « harmoniques » sont caractérisés par cette structure très régulière du spectre, figure 4.

Source - © 2012 V. Vidal

Figure 4. Signaux dits « harmoniques » et « non harmoniques »

La question est maintenant : quel mécanisme physique permet de générer la structure régulière du spectre d'un signal harmonique ?

Prenons comme premier exemple la guitare. Lorsque l'on pince une corde, on la met en vibration.

On cherche maintenant à analyser le phénomène.

La vibration de la corde correspond à une superposition de plusieurs vibrations possibles que l'on appelle les modes propres de vibration de la corde. Les modes propres sont fixés par les conditions aux limites du système. Les possibilités de vibrations sont présentées ci-dessous :

La figure 6 présente les différents modes propres de vibration d'une corde fixée à ses 2 extrémités. A chaque mode correspond une longueur d'onde, donc une fréquence : f pour le fondamental, puis 2f, 3f, etc.

Dans le cas d'une corde fixe, les fréquences propres du système sont des multiples entiers de la fréquence fondamentale.

On peut également obtenir un signal harmonique avec un processus physique un peu différent.

On peut modéliser la flûte traversière au premier ordre comme un tuyau ouvert aux deux extrémités. Quand on souffle dans ce tuyau on va exciter des modes de vibration de l'air. De part la modélisation, l'air est libre de bouger aux deux extrémités, la condition de vitesse est alors maximale aux extrémités, et la condition de pression nulle à ces mêmes points.

On retrouve, figure 7, les modes propres de vibration de la colonne d'air correspondant à f, 2f, 3f, etc.

Encore une fois, tout comme la corde de guitare, les conditions aux limites fixent les modes propres du système. Les conditions aux limites symétriques donnent un rapport 1, 2, 3, ou plus généralement des entiers multiples de la fréquence fondamentale du système.

La flûte à bec peut se modéliser au premier ordre comme un résonateur avec des conditions aux limites asymétriques : un tuyau ouvert à une extrémité et fermé à l'autre. Dans ce cas, à l'extrémité fermée la vitesse s'annule (les molécules ne peuvent pas bouger) et la pression est maximale.

Si l'on regarde cette fois-ci les modes propres de la résonance dans le tuyau, on ne va retrouver que des multiples impairs de la fréquence fondamentale, les autres modes étant interdits par la géométrie du système.

Ainsi la présence des harmoniques dans un signal va être pilotée par les conditions aux limites du système étudié.

Pour voir en ligne le film de la conférence, synchronisé avec les diapositives et le plan de la conférence : « Le chant de la Terre : écouter et modéliser les volcans » (durée : 1 h 04 min).