Résolution numérique en langage python : Équation de la diffusion de la chaleur

Pour résoudre numériquement l'équation de diffusion, il est nécessaire de la discrétiser dans le temps et dans l'espace.

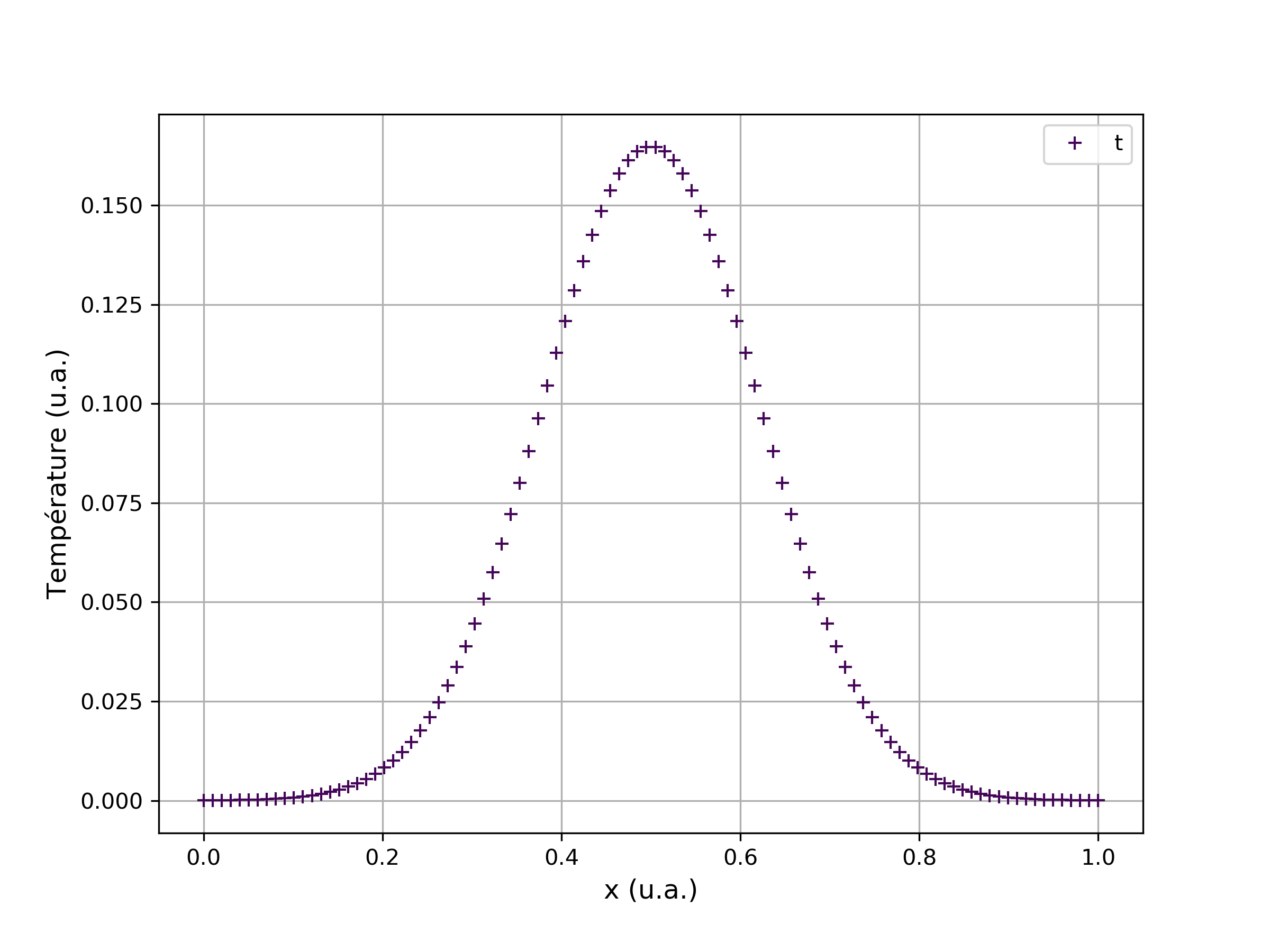
À chaque instant t nous avons un profil de température dont la valeur est donnée dans l'espace pour tous les points, x, x+dx, etc., figure 1.

Figure 1.  Profil de température à l'instant t

À partir du profil de température à l’instant t, nous allons calculer les valeurs de température à l’instant t+dt, pour tous les points de l'espace, figure 2.

Figure 2.  Profil de température à l'instant t+dt

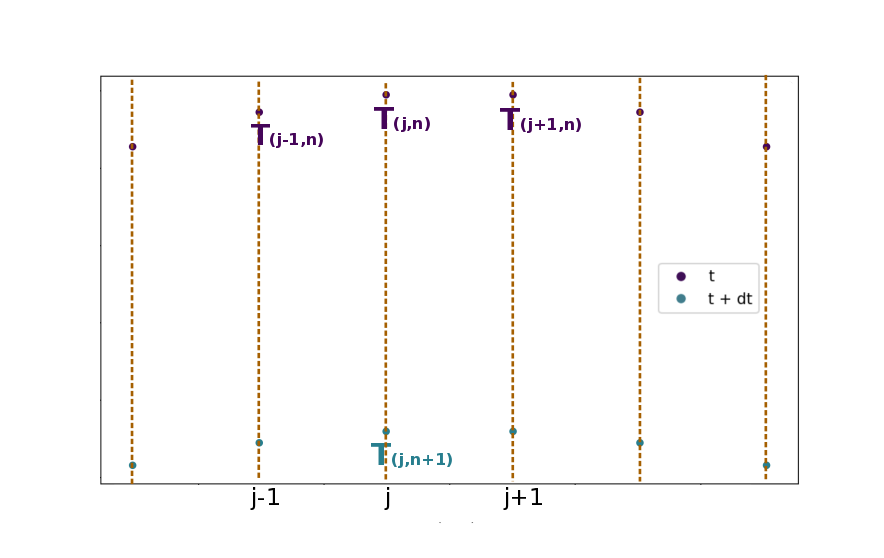
Pour l’écriture de l’algorithme, on utilisera \(T(~j, n)\) l'approximation numérique de \(T(x_j, t_n)\), avec l'indice j correspondant à l'espace et l'indice n au temps. En chaque point de l’espace les valeurs de la température seront calculées successivement à partir de la connaissance des valeurs à l’instant précédent.

Pour calculer la température \(T\) en \(j\), à l’instant \(n+1\), nous aurons besoin des valeurs de la température en \(j-1\), \(j\) et \(j+1\) de l’instant \(n\) [1] [2].

Pour la discrétisation de l'équation on s'inspire du développement de Taylor. Le terme de gauche est une équation différentielle du premier degré. Le schéma d'Euler donne au premier ordre : \( T(~j,n+1) \approx T(~j,n) + dt \frac{\partial T(~j,~n)}{\partial t} \) D'où : \( \boxed{\frac{\partial T(~j,n)}{\partial t} \approx \frac{T(~j,n+1) - T(~j,n)}{dt}} \) Le terme de droite est une dérivée seconde. On peut écrire la différence centrée spatiale : \( T(~j+1,n) \approx T(~j,n) + dx \frac{\partial T(~j,n)}{\partial x} + \frac{dx^2}{2!} \frac{\partial^2 T(~j,n)}{\partial x^2} \) \( T(~j-1,n) \approx T(~j,n) - dx \frac{\partial T(~j,n)}{\partial x} + \frac{dx^2}{2!} \frac{\partial^2 T(~j,n)}{\partial x^2} \) On arrive à : \( \boxed{\frac{\partial^2 T(~j,~n)}{\partial x^2} \approx \frac{T(~j+1,n) - 2 T(~j,n) +T(~j-1,n) }{dx^2}} \) Finalement l'équation de la diffusion devient : $$ \boxed{ \frac{T(~j,n+1) - T(~j,n)}{dt} = D \frac{T(~j+1,n) - 2 T(~j,n) +T(~j-1,n) }{dx^2}} $$

Figure 3.  Zoom sur les valeurs de températures à l'instant t et t+dt pour la discrétisation de l'équation de diffusion en une dimension de l'espace

Il est important de vérifier la stabilité d'un schéma lorsque les valeurs sont calculées de façon itérative. En effet, chaque calcul est réalisé avec une précision finie et est donc sujet à une erreur d'arrondie. Un schéma itératif est dit stable si les perturbations de la solution numérique ne sont pas amplifiées au cours des itérations [1].

Le critère de stabilité de cette méthode est donné par la condition [1] : \( dt ≤ \frac{dx^2}{2D} \)

Il sera donc important de respecter ce critère pour le choix des paramètres numériques de la grille spatiale (dx) et du pas de temps (dt).

Dans un premier temps nous importons les bibliothèques nécessaires au traitement des données et à l'affichage des graphiques, figure 4. Nous utiliserons aussi la fonction erf pour initialiser le système.

Figure 4.  Importation des bibliothèques python utilisées

On renseigne les différents paramètres pour la résolution : la diffusivité thermique (D), le temps total d'intégration (Temps), le nombre de points de la grille temporelle (NTemps), le pas de temps (dt), la taille du domaine spatial (L), le nombre de points de la grille spatiale (NX) et le pas d'espace (dx), figure 5. On définit deux vecteurs (t et x) respectivement pour le temps et pour l'espace qui nous serviront lors du tracé des graphes. Nous utiliserons des unités arbitraires (u.a.).

Figure 5.  Initialisation des grandeurs numériques

Nous vérifions que les paramètres choisis répondent effectivement au critère de stabilité de notre schéma, figure 6.

Figure 6.  Vérification du critère de stabilité

On a bien, en effet : \( dt ‹ \frac{dx^2}{2D} \).

On choisit de partir d'une situation initiale où le corps 1D que l'on étudie est chauffé en en son centre (autour de l'abscisse 0).

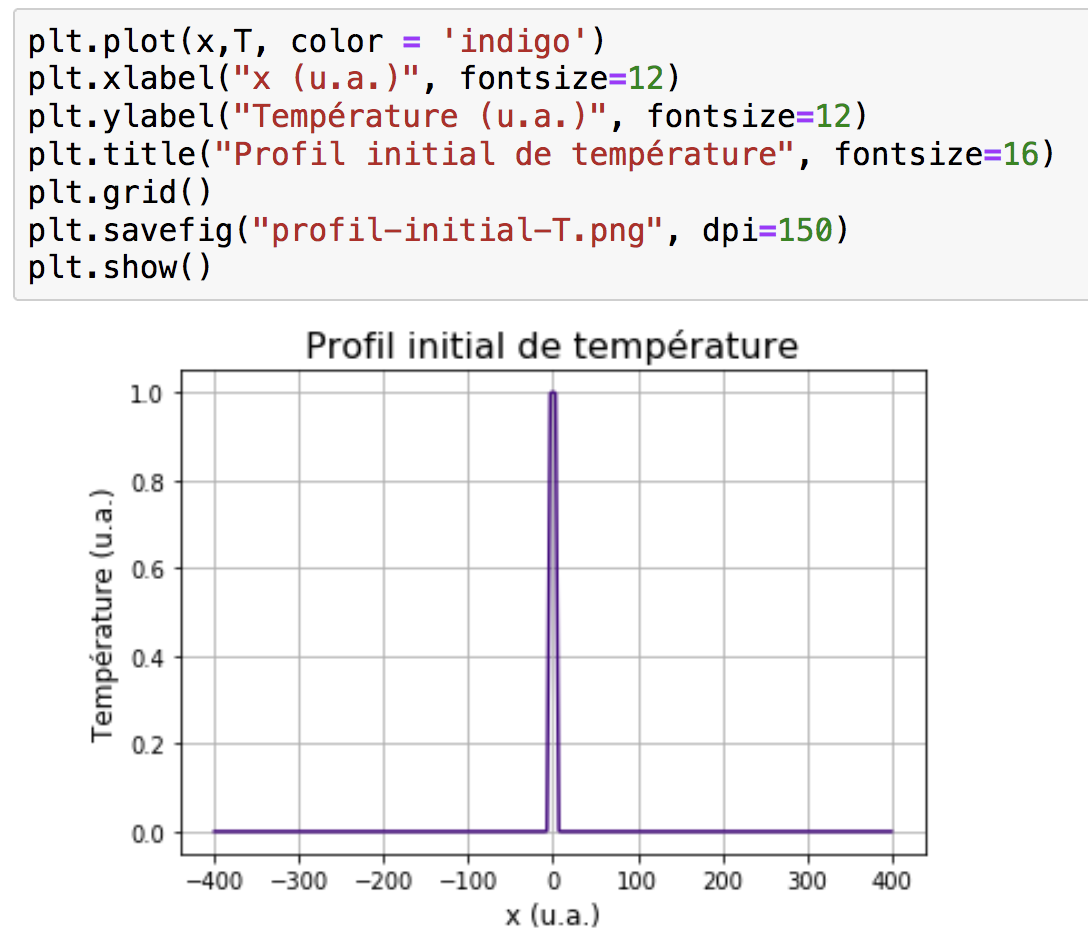
On utilise la fonction d'erreur de Gauss (noté erf) pour initialiser le profil de température, figures 7 et 8. C'est comme si l'objet était chauffé en son centre à une température de 1 (en unités arbitraires) à t = 0.

Figure 7.  Définition des conditions initiales

La représentation graphique du profil initial de température est donnée figure 8.

Figure 8.  Représentation graphique du profil de température à l'instant t = 0

Maintenant, il s'agit de coder l'équation de diffusion discrétisée :

$$ \frac{T(~j,n+1) - T(~j,n)}{dt} = D \frac{T(~j+1,n) - 2 T(~j,n) +T(~j-1,n) }{dx^2} $$

Le code est présenté figure 9, dans la boucle principale. On intègre dans le temps à l'aide de la variable n, de 0 au temps total et, pour chaque pas de temps on vient calculer la valeur de la température en tout point de la grille spatiale. Attention, comme les indices varient entre j-1 et j+1 le calcul est réalisé pour des indices j dont les valeurs sont comprises entre 1 et NX-1. les conditions aux bords sont fixées, pour j = 0 et j = NX, on impose T = 0.

On calcule le membre de droite (MD) de l’équation de diffusion, cela revient à remplir la matrice MD pour chaque point de la grille.

On calcule ensuite en tous les points la température (matrice T) au pas n+1 en fonction de la température au pas n. La notation utilisant "+=" équivaut à T[j] = T[j] + MD[j]*dt.

Figure 9.  Algorithme de la résolution numérique de l'équation de diffusion

Il est à noter que si ces lignes permettent de bien comprendre l'opération réalisée, le code n'est pas optimal. On pourra consulter la section 4.2.2 de Résolution numérique de l'équation de diffusion - python prepa github [3].

En remplaçant les boucles sur le maillage spatial par des expressions vectorielles le calcul est beaucoup plus rapide [3].

Nous choisissons aussi de stocker tous les calculs des profils de température pour chaque pas de temps dans la matrice "Theta" : chaque colonne correspond à un temps donné, le nombre de lignes correspond à la grille spatiale, figure 10.

Figure 10.  Code de la résolution numérique de l'équation de diffusion

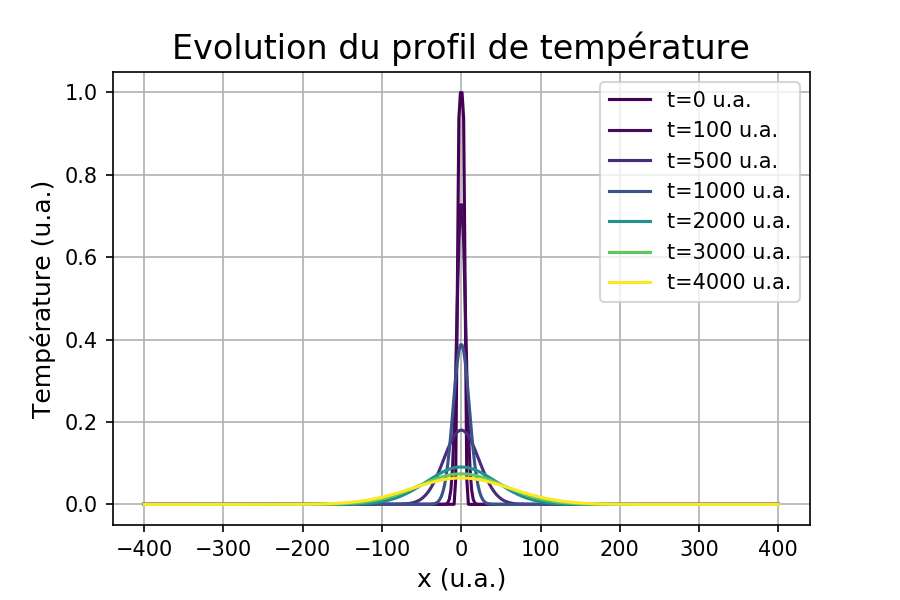
Sur la figure 11, on présente le profil de température pour quelques valeurs de temps (en unités arbitraires).

Figure 11.  Tracé du profil de température pour quelques valeurs de temps

À l'aide de la fonction FuncAnimation on peut créer une animation de l'évolution du profil de température, figures 12 et 13.

Figure 12.  Code pour créer un gif animé des profils de température

Figure 13.  Évolution du profil de température en unités de temps arbitraires

Si l'on ne respecte pas le critère de stabilité de l'algorithme, on peut mettre en évidence la génération spontanée d'instabilités et la divergence du code.

En prenant par exemple L = 4, on a alors \( \frac{dx^2}{2D} \) = 5.10^-5 qui est inférieur à \( dt \) = 7,5.10^-5.

On constate, au bout de quelques itérations, figures 14 et 15, que les valeurs du calcul des températures dépassent les valeurs des conditions initiales, ce qui est physiquement incorrect.

Figure 14.  Mise en évidence d'instabilités du schéma (6ème itération)

Figure 15.  Mise en évidence d'instabilités et de divergence du schéma (14ème itération)

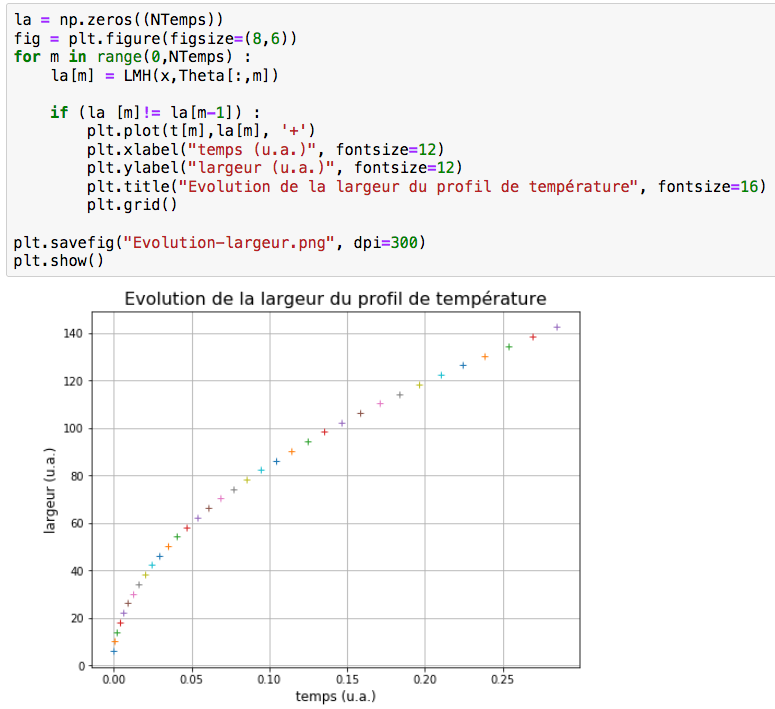
On s’intéresse maintenant à l’évolution de la largeur du front de diffusion. On calcule la largeur à mi-hauteur de la tache de diffusion au cours du temps, à l'aide de la fonction LMH que l'on définit figure 16. On va se servir de la fonction sign qui détermine le signe de la valeur de la largeur à mi-hauteur moins la valeur en tous les points du profil de température. Le signe sera négatif ( d == -1) pour tous les points j correspondants à la largeur à mi-hauteur.

Figure 16.  Evolution de la largeur du profil de température en fonction du temps

On trace la largeur à mi-hauteur en fonction du temps, figure 17. L'espace n'étant pas défini avec une haute résolution (pour favoriser la rapidité du calcul), la largeur du profil est représentée à chaque fois qu'elle change. On observe qu'elle augmente de plus en plus lentement avec le temps.

Figure 17.  Evolution de la largeur du profil de température en fonction du temps

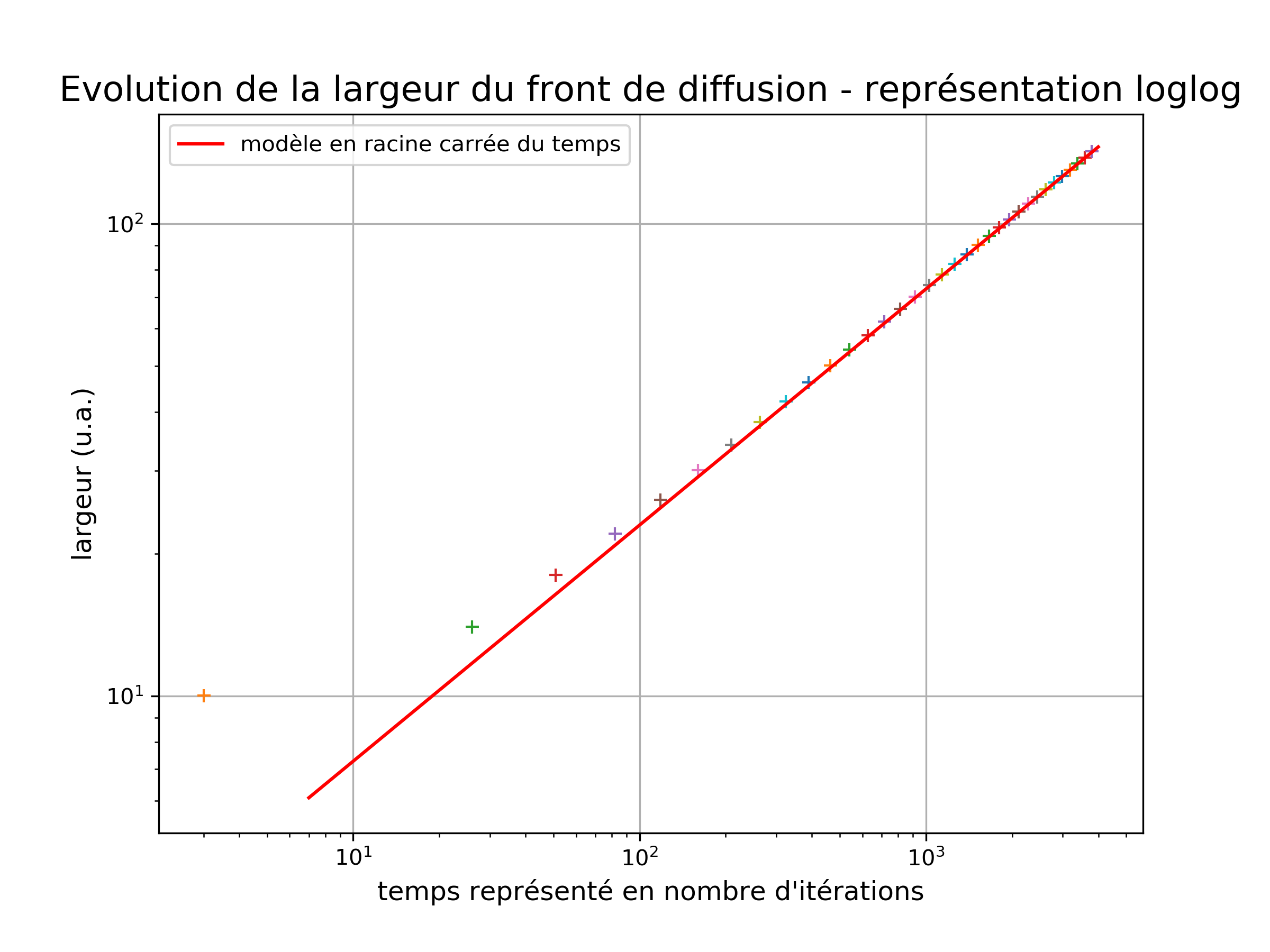
Afin de vérifier que le front de température suit bien une loi proportionnelle à la racine du temps, figure 18, on peut superposer le résultat de la résolution numérique avec une fonction variant en racine carrée du temps en représentation log-log, figure 19. Le temps en abscisse est représenté ici sous la forme du nombre d'itérations du calcul.

Figure 18.  Evolution de la largeur du profil de température en fonction du temps, ajustement avec une fonction qui varie en racine du temps

Figure 19.  Evolution de la largeur du profil de température en fonction du temps, représentation loglog, ajustement avec une fonction qui varie en racine du temps

Pour les temps longs, nous retrouvons que la largeur de la zone de diffusion augmente selon la racine carrée du temps.