Activer le mode zen
Ressource au format PDF
Mots-clés
Classification
Hand spinner
24/06/2019
Travail réalisé dans le cadre des XXVIe Olympiades de Physique sous la tutelle de Jean-Brice Meyer, professeur de Physique-Chimie.
Résumé
« Hand spinner » est un projet au cours duquel nous avons voulu étudier en détail la rotation de cet objet. Même si certains processus sont rapidement identifiables, il n’est pas forcément évident d’arriver à les quantifier, aussi bien sur un plan expérimental que théorique. C’est pourtant ce que nous avons tenté de faire. Et c’est ainsi, en entrant dans le vif du sujet, que nous avons pu dépasser les quelques notions perceptibles en premier abord.
En cherchant à déceler les secrets du hand spinner, nous avons même été confronté à des phénomènes dont nous ne nous doutions pas. Cet objet est finalement plus qu’un simple jouet... ou un vrai jouet puisqu’il nous a permis de nous amuser tout en faisant des sciences de façon plus poussée qu’on ne l’aurait imaginé.
Table des matières
- 1. Introduction
- 2. De quels paramètres dépend la durée de rotation du hand spinner ?
- 3. Quelles sont les contributions des frottements fluides et solides dans la durée de rotation du hand spinner ?
- 4. Quels autres phénomènes peuvent affecter la vitesse de rotation du hand spinner ?
- 5. Comment repousser la limite de vitesse de rotation du roulement à bille ?
- 6. Conclusion
1. Introduction
Le hand spinner connaît son heure de gloire. Le choix d’acquérir un hand spinner plutôt qu’un autre peut se faire selon différents critères, comme son esthétique ou bien ses performances. Mais justement, de quoi dépendent les performances d’un hand spinner ?
C’est ce que nous avons voulu savoir et que nous évoquons dans cet article.
2. De quels paramètres dépend la durée de rotation du hand spinner ?
2.1 Description du hand spinner
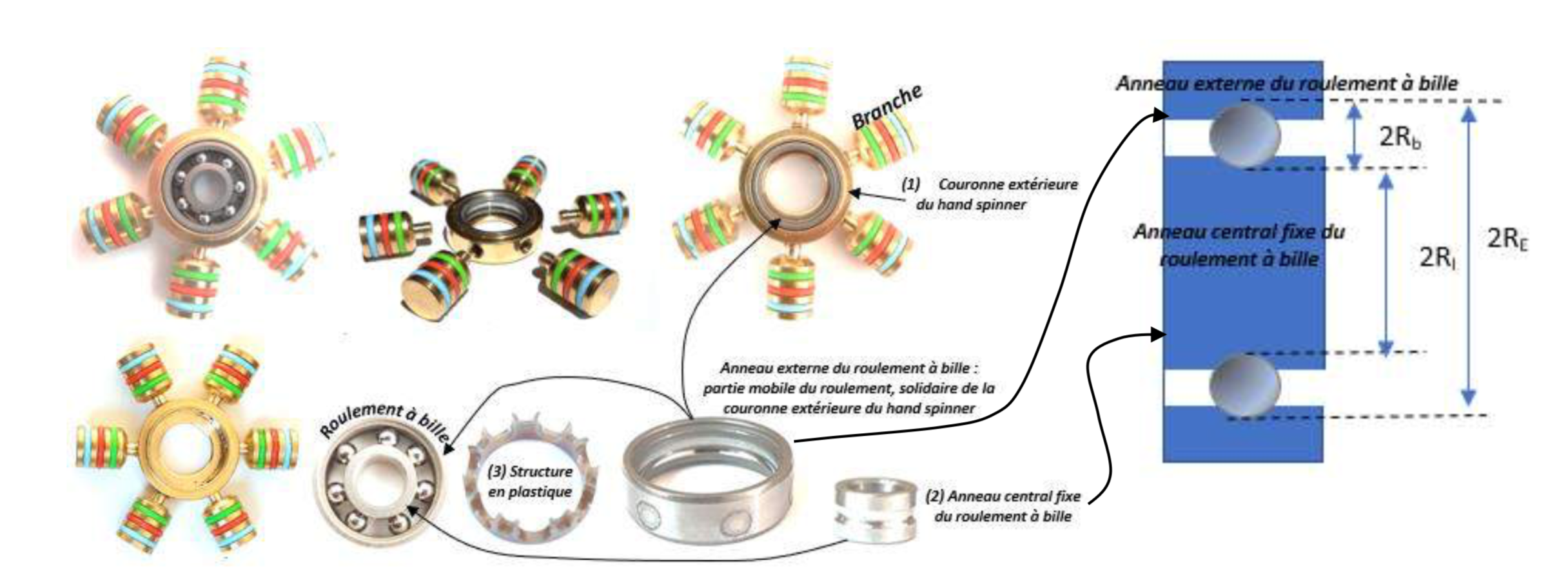
Nous avons fait l’acquisition de plusieurs hand spinners identiques qui ont la particularité de pouvoir être démontés entièrement, ce qui va être très utile pour mener à bien cette étude (figure 1).
Le hand spinner contient 6 branches qui se vissent sur la couronne extérieure (1). À l’intérieur du hand spinner se trouvent les 7 billes du roulement, ainsi qu’un anneau central (2) fixe. Pour maintenir les billes dans leurs positions respectives, celles-ci sont disposées dans une structure en plastique (3).
Nous avons eu besoin, au cours de notre projet, de connaître avec précision certaines dimensions de ces différents éléments. Nous avons réalisé les mesures avec un pied à coulisse donnant des longueurs avec une précision au centième de millimètre. Voici quelques mesures obtenues :
- Rayon interne de l’anneau externe en enlevant la profondeur du sillon dans lequel roule la bille : RE = 9,42 mm
- Rayon de l’anneau central en enlevant la profondeur du sillon dans lequel roule la bille : Ri = 5,64 mm
- Rayon de la bille : Rb = 3,78/2 mm
2.2 Influence de la masse sur la durée de rotation du hand spinner
Le hand spinner dont nous disposons contient 6 branches démontables. Nous avons enlevé des branches, en faisant en sorte que le centre d’inertie du hand spinner reste toujours au même endroit, pour mesurer, pour une vitesse de rotation initiale identique, la durée de rotation du hand spinner.
Comme nous ne pouvons pas lancer le hand spinner toujours à la même vitesse, nous avons choisi de mesurer la durée de la rotation à partir d’une date t = 0 de sorte qu’elle corresponde à une vitesse identique du hand spinner pour les 4 lancés. Pour connaître la vitesse du hand spinner au cours du temps, nous avons filmé la rotation avec une caméra à 240 images par seconde. Nous avons alors exploité les vidéos avec le logiciel Latis Pro, figure 2.
Nous observons que plus la masse est importante, pour une vitesse initiale identique, plus la rotation dure longtemps. Mais en réalité, ce n’est pas si simple que cela.
En effet, il est possible de disposer les branches du hand spinner plus éloignées de 2 millimètres du centre d’inertie en jouant sur le pas de vis. En faisant cela, on ne change pas la masse du hand spinner. Et pourtant, nos mesures montrent que la rotation dure plus longtemps. Il est alors clair que la masse, mais aussi la façon dont elle se répartit dans le système, a une importance dans la rotation du hand spinner. Ceci montre l’importance d’une caractéristique du hand spinner : son moment d’inertie, que nous noterons I∆.
Nous avons alors dû, lors de ce projet, nous familiariser avec de nouvelles notions :
Le moment d'inertie d'un système :
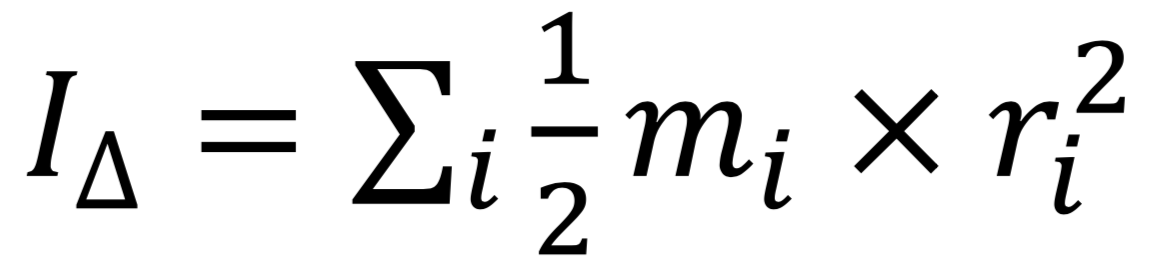
Il dépend de la masse du système mi et de la façon dont cette masse se répartit (distance ri) par rapport à l'axe de rotation du système.
Le moment cinétique d'un système :
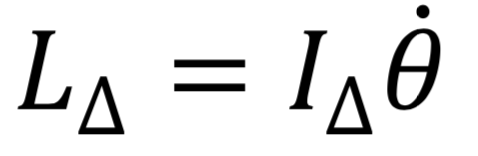
Où
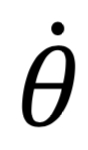 représente la vitesse angulaire du système.
représente la vitesse angulaire du système.
L’énergie cinétique du système par rapport à son axe de rotation :
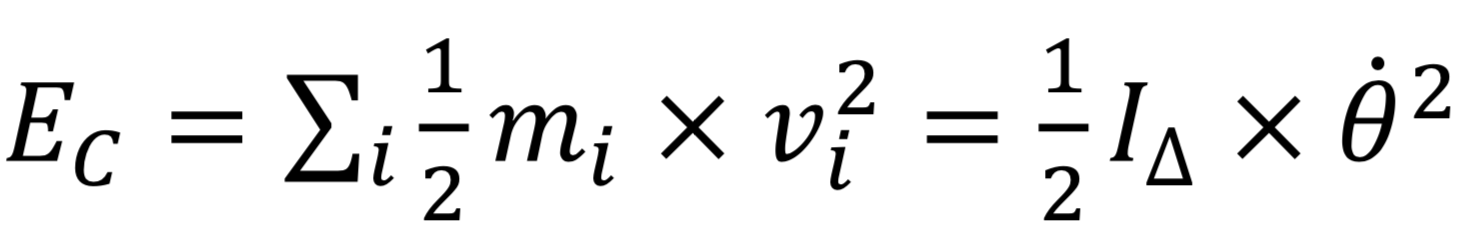
2.3 Que faut-il alors pour que le hand spinner puisse tourner le plus longtemps possible ?
Puisque le hand spinner finit par s’arrêter, c’est qu’il est soumis à des frottements, qui sont des forces non conservatives. Pour qu’il tourne le plus longtemps possible, on peut bien sûr lui donner une énergie cinétique la plus forte possible.
Compte tenu de l’expression de l’énergie cinétique :
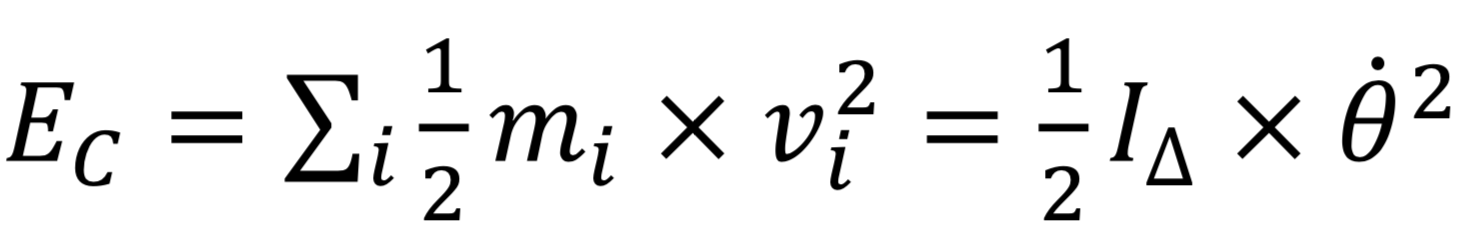
- Une grande vitesse radiale
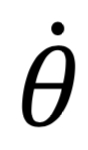 au départ, mais celle-ci est limitée par la vitesse
avec laquelle on est capable de bouger le doigt pour mettre en mouvement
le hand spinner.
au départ, mais celle-ci est limitée par la vitesse
avec laquelle on est capable de bouger le doigt pour mettre en mouvement
le hand spinner. - Un fort moment d’inertie.
Mais surtout, si l'on souhaite que le hand spinner ne s’arrête jamais de tourner, il faudrait supprimer les frottements. Même si cela est impossible, on peut les limiter en ayant des profils de hand spinner particulièrement aérodynamiques. Mais les frottements peuvent également être de nature solide et pas uniquement fluide. Peut-on quantifier la contribution des frottements fluides et solides au cours de la rotation du hand spinner ?
3. Quelles sont les contributions des frottements fluides et solides dans la durée de rotation du hand spinner ?
On s'est intéressé au spectre sonore émis par le hand spinner en rotation avec l’application « FFT Spectrum Analyser ». Nous avons filmé l’expérience réalisée avec cette application, figure 3.
Les résultats obtenus montrent clairement qu’il y a au moins deux phénomènes qui interviennent lors de la rotation du hand spinner. On remarque qu’un son de faible fréquence, compris entre 0 et environ 300 Hz est produit, et que ce son a une fréquence qui diminue au cours du temps, c’est-à-dire en même temps que le hand spinner ralentit.
D’autre part, on remarque qu’un son est aussi produit vers 1 000 Hz, ainsi qu’autour d’environ 1 700 Hz et 2 100 Hz, et que ces fréquences restent présentes et d'amplitude constante durant la rotation du hand spinner. On peut penser que le son de faible fréquence est lié à la vitesse de rotation du hand spinner, et que le son représenté par les fréquences plus élevées, qui restent constantes quelle que soit la vitesse du hand spinner, serait alors dû aux frottements solides.
3.1 Mesure expérimentale de l'évolution de la vitesse de rotation du hand spinner au cours du temps
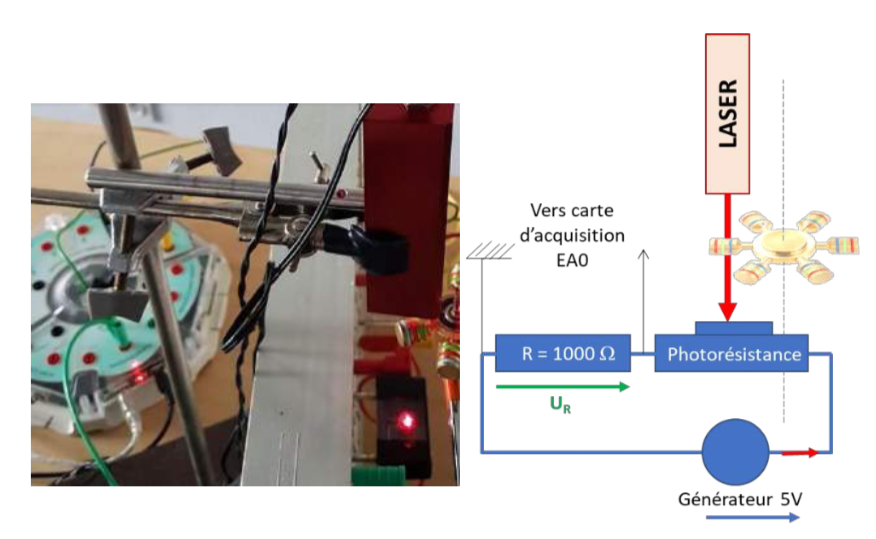
Pour étudier les frottements, nous avons voulu connaître précisément l’évolution de la vitesse de rotation du hand spinner au cours du temps, figure 4.
Nous avons utilisé un faisceau laser et une photorésistance. Lorsque le hand spinner tourne, ses branches coupent tour à tour le faisceau laser, cela provoque une augmentation de la résistance de la photorésistance, donc une diminution de l’intensité du courant, et par suite, une diminution de la tension aux bornes de la résistance.
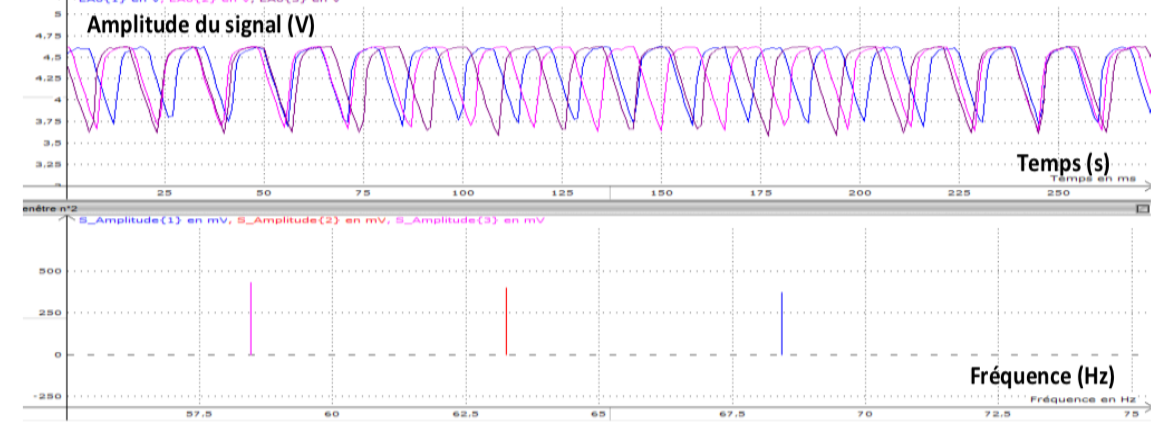
Pendant la rotation du hand spinner, nous avons réalisé un grand nombre d’acquisitions à différents instants. Nous avons superposé les mesures dans une même fenêtre. Sur la figure 5, nous avons, par exemple, trois acquisitions à trois dates différentes. Pour en déduire les vitesses de rotation, nous avons réalisé les analyses de Fourier de ces signaux.
En divisant ces fréquences F par 6, du fait de la présence des 6 branches, nous pouvons alors en déduire la vitesse de rotation du hand spinner :
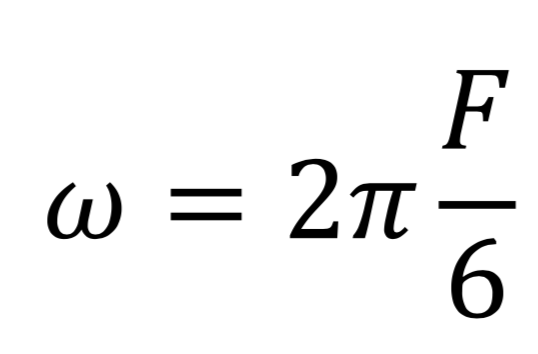
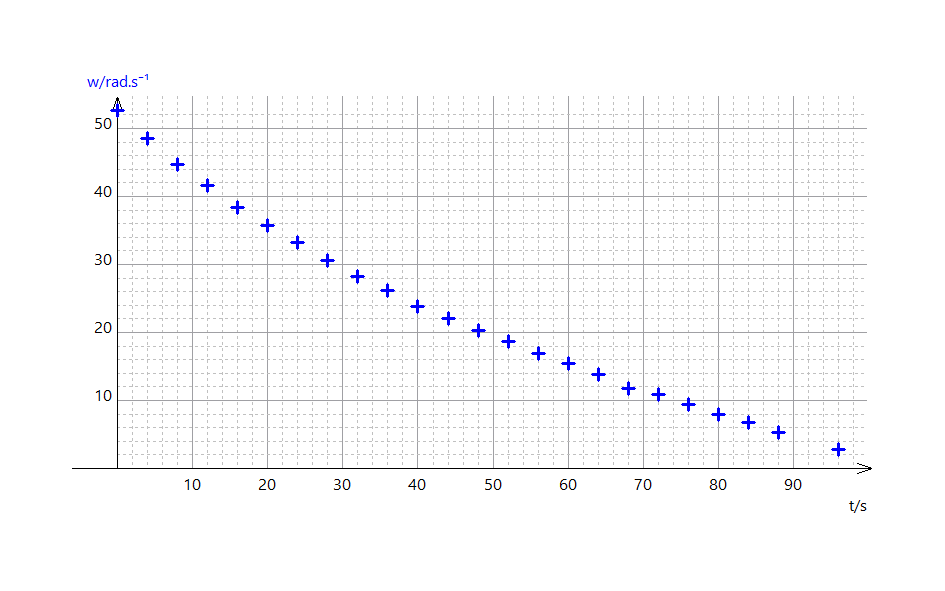
Nous avons réalisé plus d'une vingtaine d'acquisitions, avec une période d'échantillonnage de 4 secondes, durant la rotation du hand spinner. Cela nous a permis de mesurer l’évolution de la vitesse angulaire du hand spinner, figure 6.
3.2 Exploitation des résultats
a) Mise en équation
Nous considérons ici que le système étudié est la couronne extérieure du hand spinner, avec les 6 branches. Le système est soumis à son propre poids, aux frottements avec l’air et aux frottements solides avec les billes.
Nous allons supposer dans un premier temps que les forces de frottements
solides engendrent un couple résistant ![]() indépendant de la vitesse de rotation de la couronne
extérieure. D’autre part, nous faisons l’hypothèse que les forces de frottements
fluides sont le siège d’un couple résistant
indépendant de la vitesse de rotation de la couronne
extérieure. D’autre part, nous faisons l’hypothèse que les forces de frottements
fluides sont le siège d’un couple résistant ![]() proportionnel à la vitesse angulaire.
proportionnel à la vitesse angulaire.
Ces couples conduisent à une diminution du moment cinétique du système, conformément au théorème du moment cinétique :
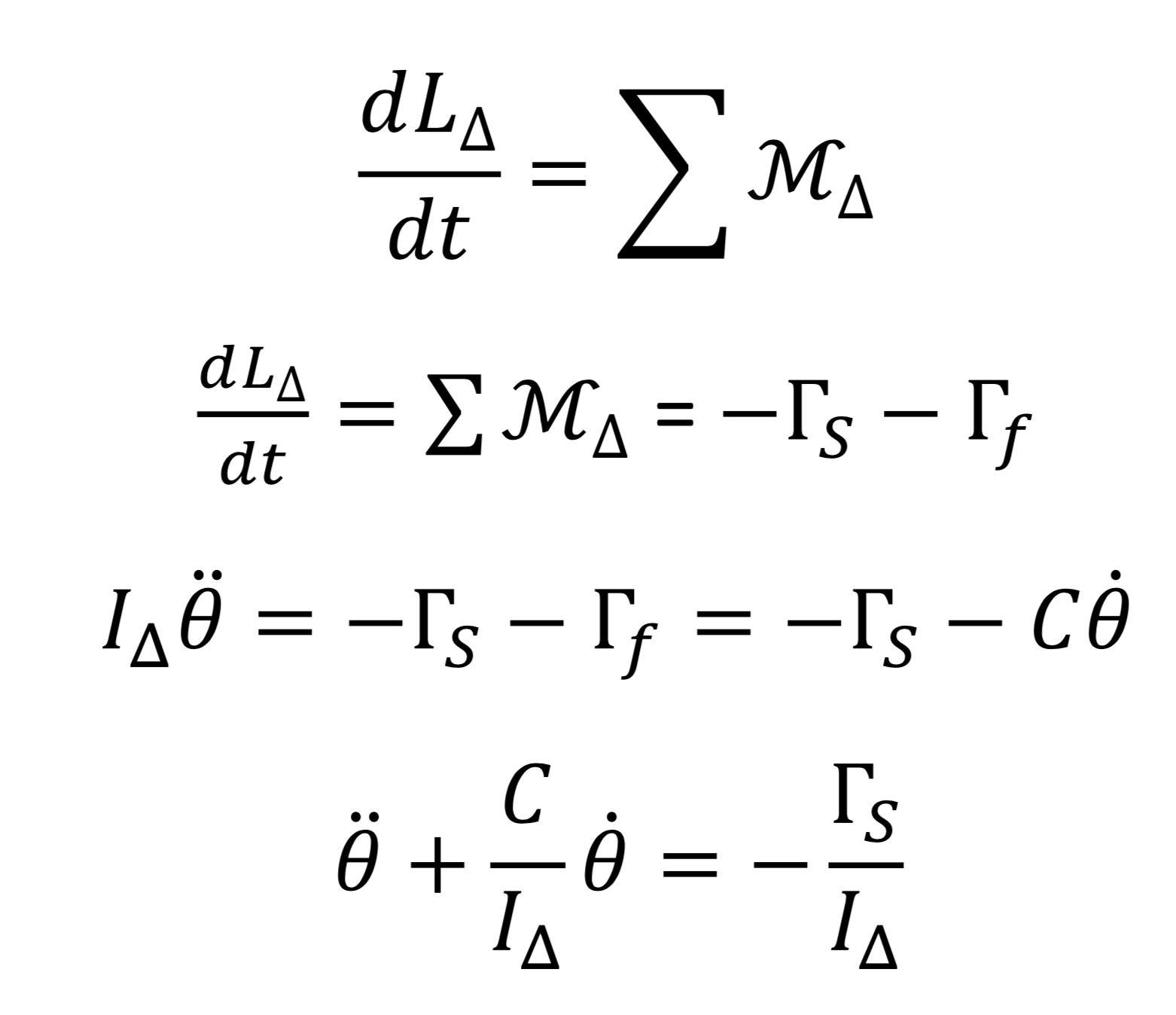
La solution de cette équation différentielle est donc de la forme :
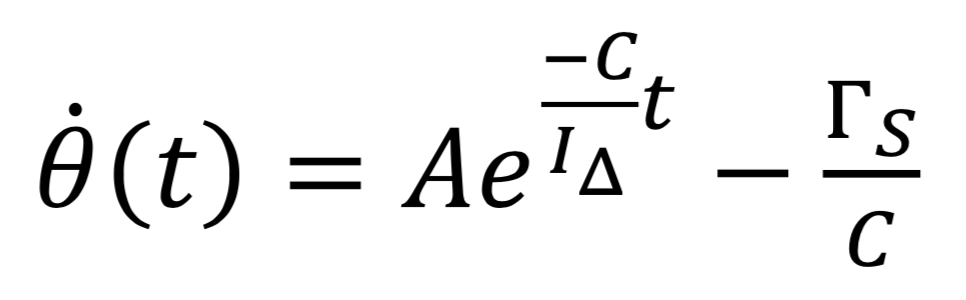
Ainsi, en appelant ![]() la vitesse angulaire à l’instant t0
de l’acquisition, on obtient :
la vitesse angulaire à l’instant t0
de l’acquisition, on obtient :
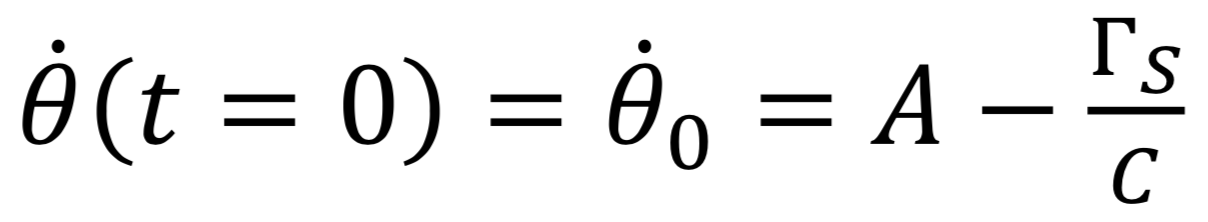
Donc :
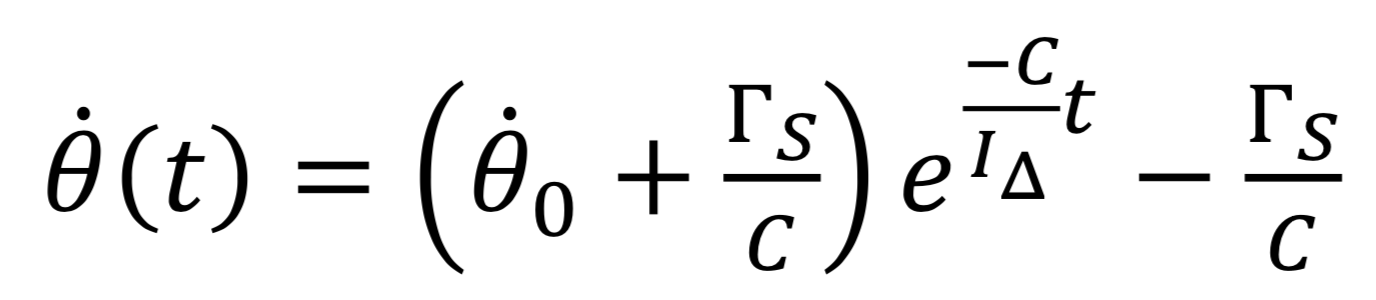
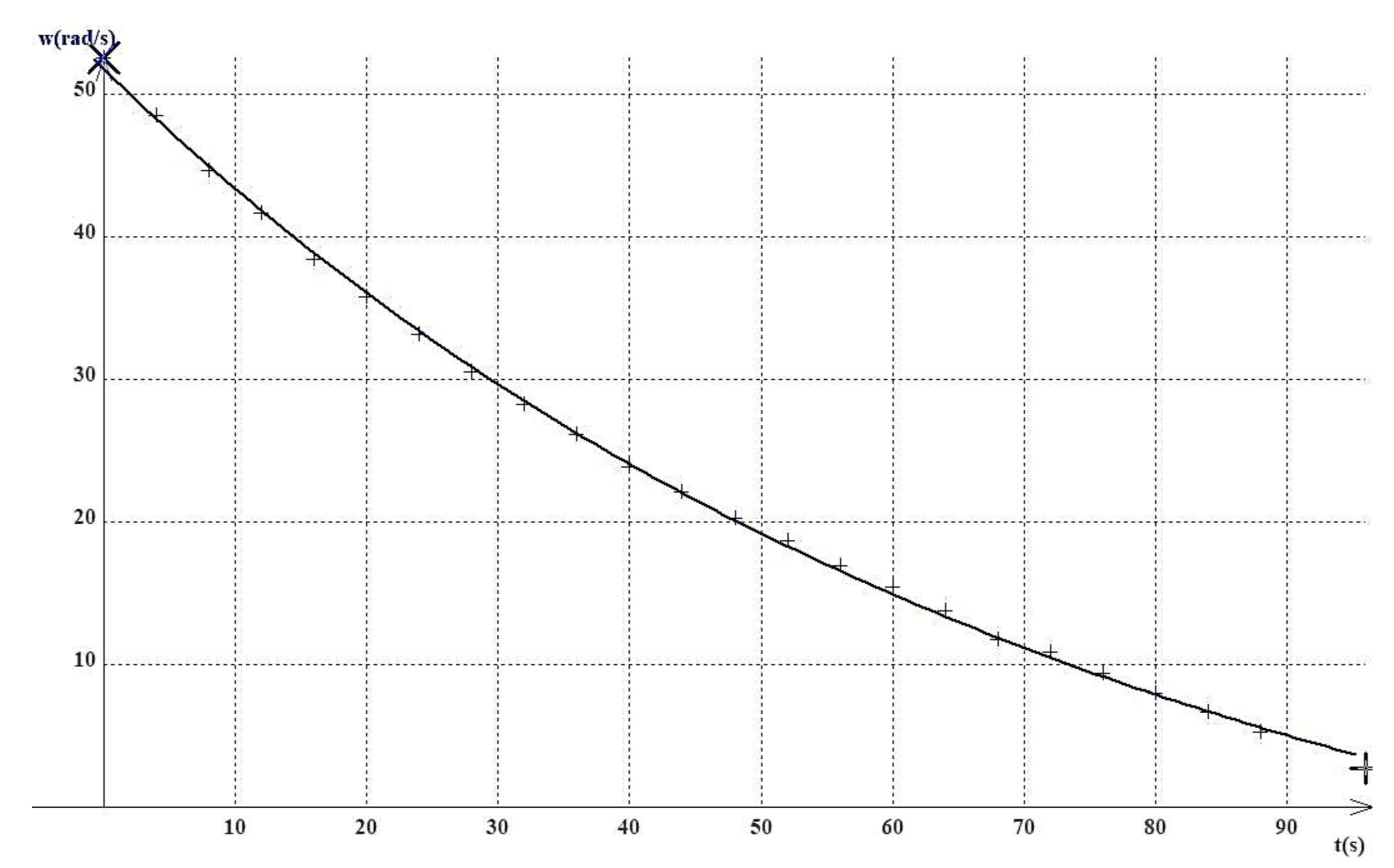
Nous modélisons les résultats expérimentaux, figure 7.
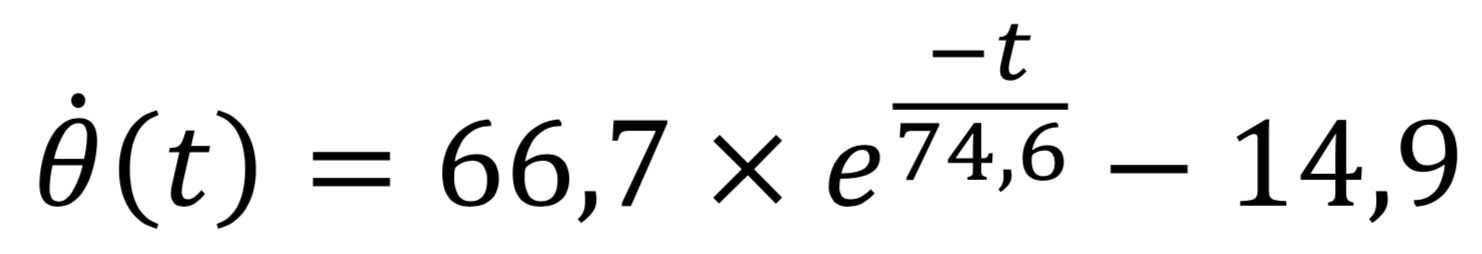
Le modèle est donc plutôt cohérent avec les valeurs expérimentales, ce qui nous conforte dans les hypothèses que nous avons formulées : le système est bien soumis à deux forces de frottements, solides et fluides, dont les expressions semblent être celles que nous avons proposées.
Nous pouvons exploiter davantage la modélisation en estimant les couples résistants. Nous en déduisons que :
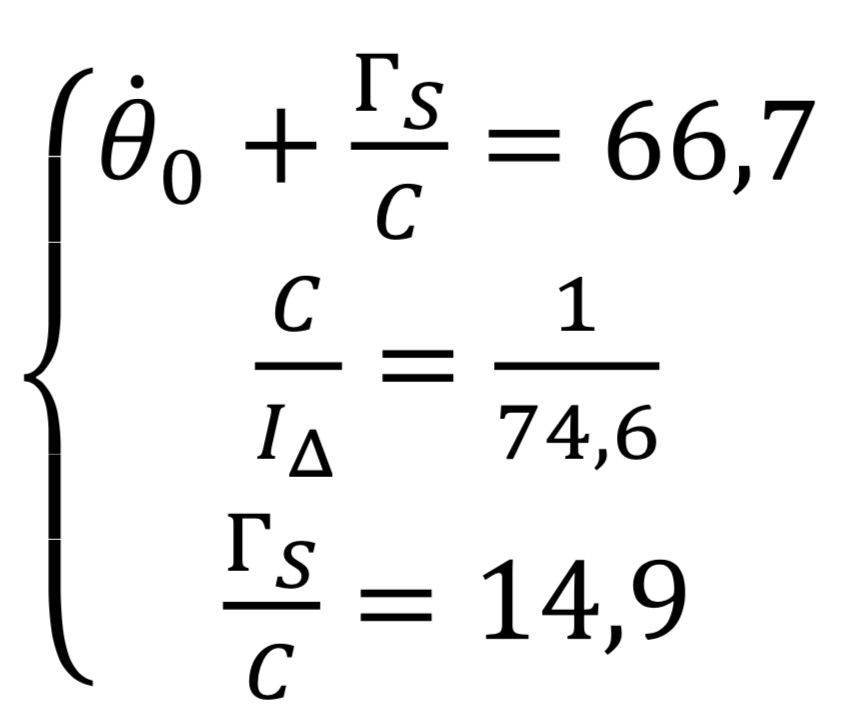
![]() s'obtient sur la courbe : on lit 51,9 rad/s.
s'obtient sur la courbe : on lit 51,9 rad/s.
Mais pour autant, ces équations ne suffisent pas. Si l'on veut déterminer les couples résistants solide et fluide, il nous faut connaître le moment d’inertie IΔ du système.
b) Moment d'inertie du hand spinner
Nous rappelons ici que le système dont nous voulons déterminer le moment d’inertie est la couronne extérieure du hand spinner, munie de ses 6 branches.
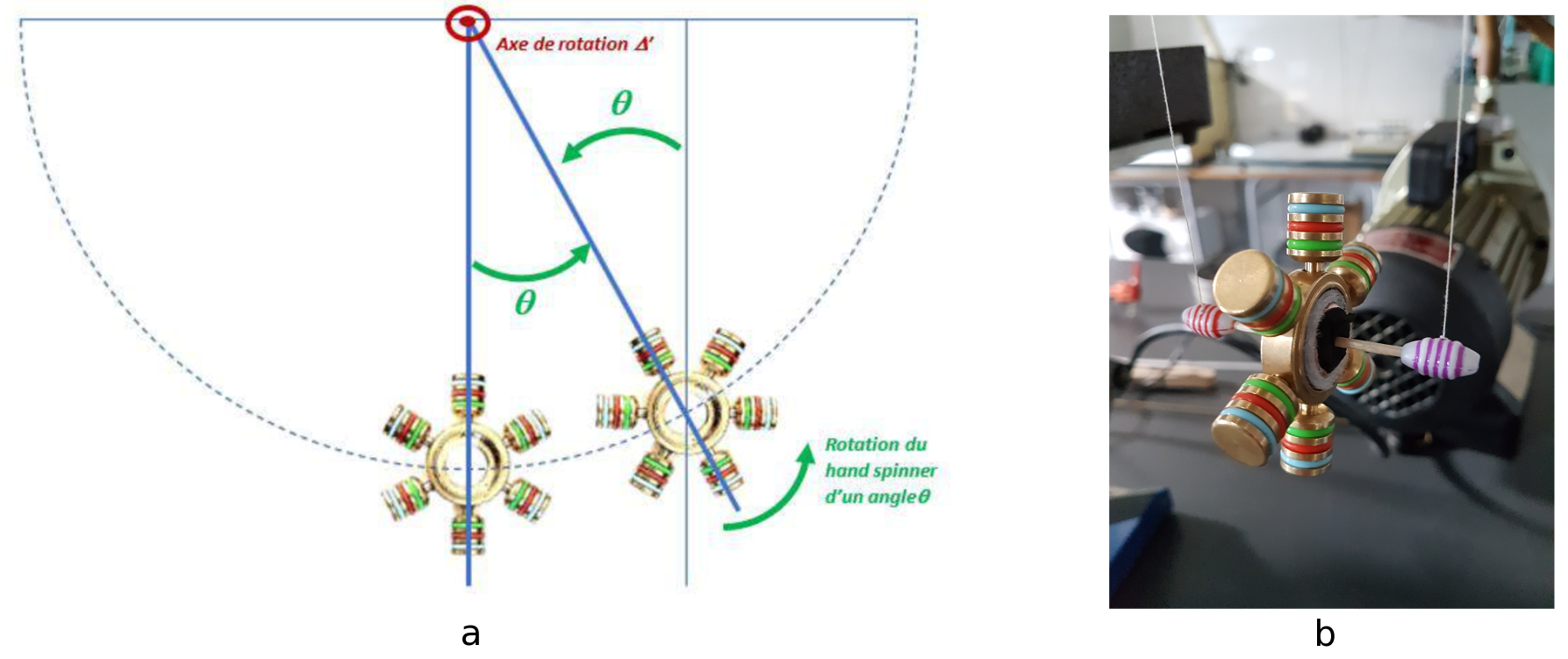
Pour cela, nous allons déduire le moment d’inertie du système par la mesure de la période des oscillations de celui-ci lorsqu’on le fait penduler de la façon suivante, figure 8. On accroche deux fils identiques de masse négligeable sur l’axe de rotation du pendule et sur une potence. On fait ensuite osciller le hand spinner.
Comme au cours de l'oscillation l’orientation du hand spinner dans un plan perpendiculaire à son axe de rotation varie avec le même angle que celui du pendule ainsi constitué, l’énergie cinétique à chaque instant est la somme de l’énergie cinétique du centre de gravité du hand spinner et de l’énergie cinétique de rotation du hand spinner. Et c’est à l’aide de cela qu’il est possible d’aboutir à la relation que nous ne ferons qu’utiliser à défaut de savoir démontrer :
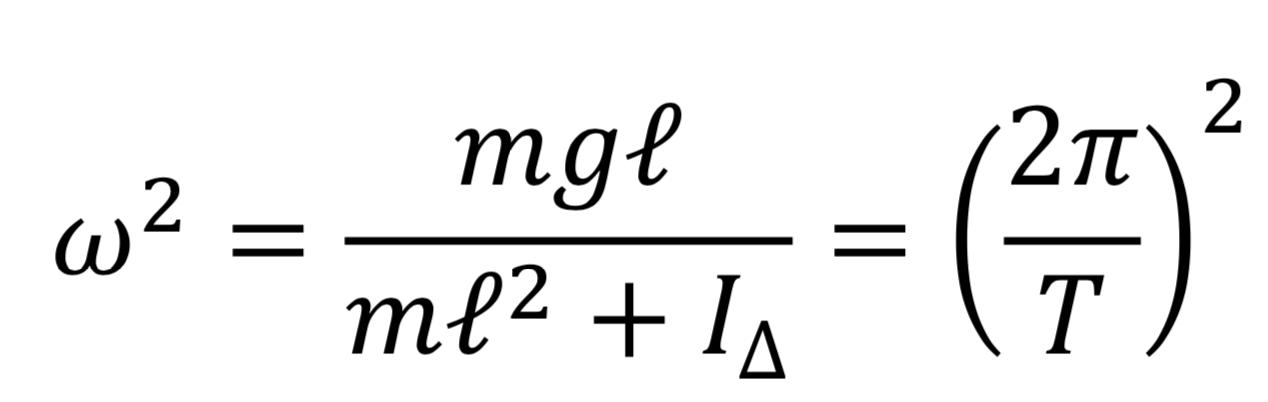
Donc :
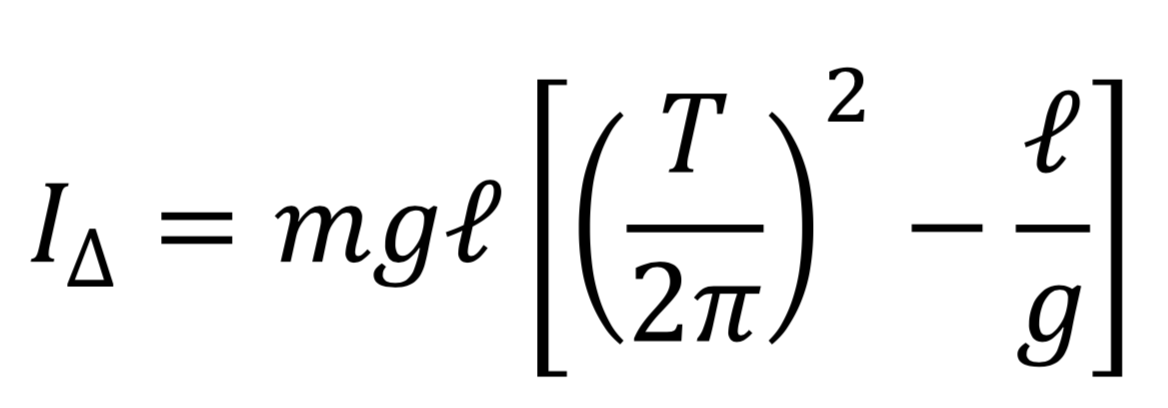
Pour des raisons expérimentales, nous avons dû procéder en deux étapes. Pour maintenir le hand spinner au niveau de son axe de rotation, alors qu’on lui a oté son roulement à billes, nous avons disposé de la matière dans le trou se trouvant au milieu du hand spinner. Nous avons gardé l’anneau extérieur du roulement à billes, tandis que nous avons enlevé les billes et l’anneau intérieur. Nous avons alors rempli l’anneau extérieur de mousse très dense, figure 8b. Ainsi, nous avons pu percer la mousse avec un pic qui la traverse de part et d’autre pour maintenir le hand spinner. Ce faisant, le moment d’inertie mesuré sera alors celui du hand spinner, plus celui de la matière que nous venons de disposer à l’intérieur du hand spinner.
Pour avoir le moment d’inertie du hand spinner seul, il suffit alors de mesurer avec la même méthode le moment d’inertie de la mousse disposée dans le hand spinner, puis de le soustraire au moment d’inertie de l’ensemble.
- La longueur du fil mesure 70,9 cm
- La masse totale du hand spinner est m = 89,10 g
- La masse du dispositif seul placé au centre du hand spinner (mousse) est m' = 3,20 g
- La période des oscillations a été mesurée de façon très précise, en filmant 30 oscillations, et en analysant la vidéo avec Latis Pro, dans un premier temps avec le hand spinner muni du dispositif central (T = 1,70 s) puis dans un deuxième temps avec uniquement la mousse (T = 1,69 s).
Avec de telles valeurs, nous avons évalué le moment d'inertie du hand spinner à IΔ = 5,76.10-4 kg/m2
On en déduit, ensuite, le couple résistant des frottements solide et le coefficient du couple résistant des frottements fluides.
c) Valeurs du couple résistant solide et du coefficient du couple résistant fluide
Voici les valeurs que nous avons obtenues de nos mesures :
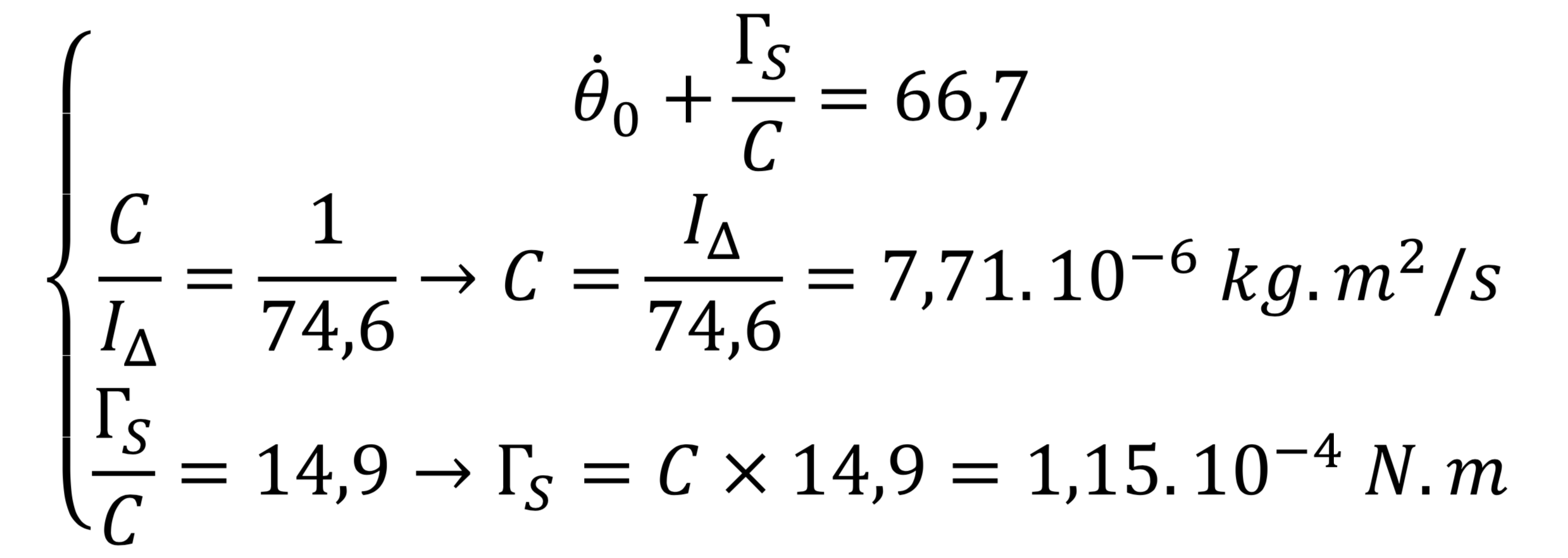
Nous avons choisi un modèle de couple de frottements proportionnel à la vitesse radiale. Mais en réalité, il se peut que ce ne soit pas le cas, ou que ce soit le cas pour certaines vitesses de rotation. Cela dit, la concordance entre le modèle choisi pour représenter les frottements, et les mesures expérimentales, ne nous a pas poussé à explorer d’autres pistes aux vitesses où nous avons fait tourner le hand spinner.
3.3 Peut-on mesurer les frottements solides sans se soucier des frottements fluides ?
Ce serait une autre façon d’étudier le hand spinner, sans se soucier du milieu dans lequel il tourne. On aurait donc une étude qui ferait intervenir uniquement des paramètres intrinsèques du hand spinner !
Du coup, pourquoi ne pas se débarrasser tout simplement de l’air ?
a) Prévision du résultat
Sans air, pas de frottements fluides. Nous nous attendons ici à trouver une évolution linéaire de la vitesse de rotation du hand spinner au cours du temps. En effet,
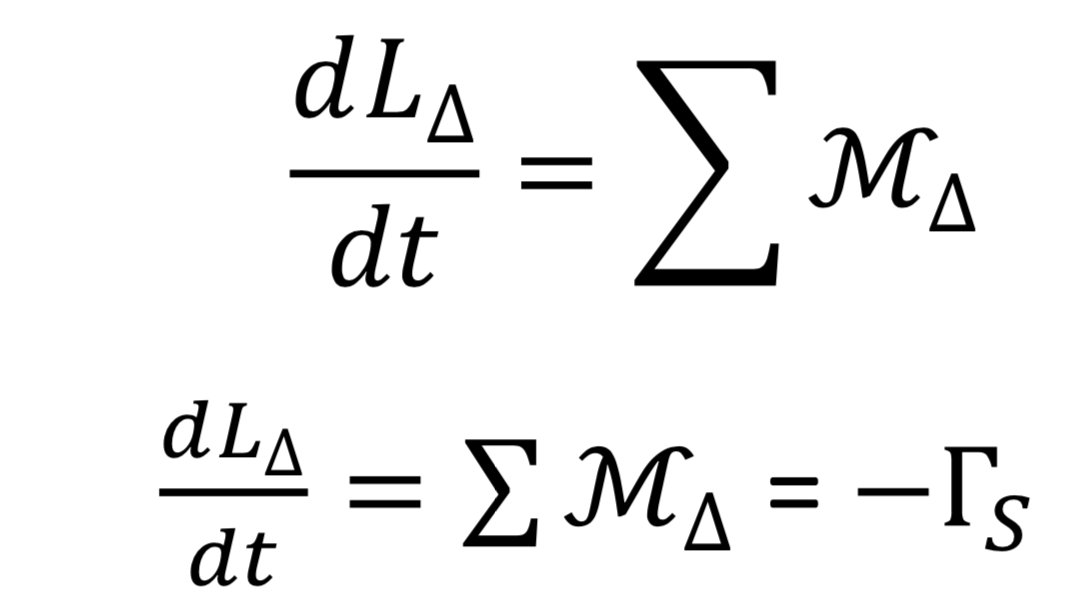
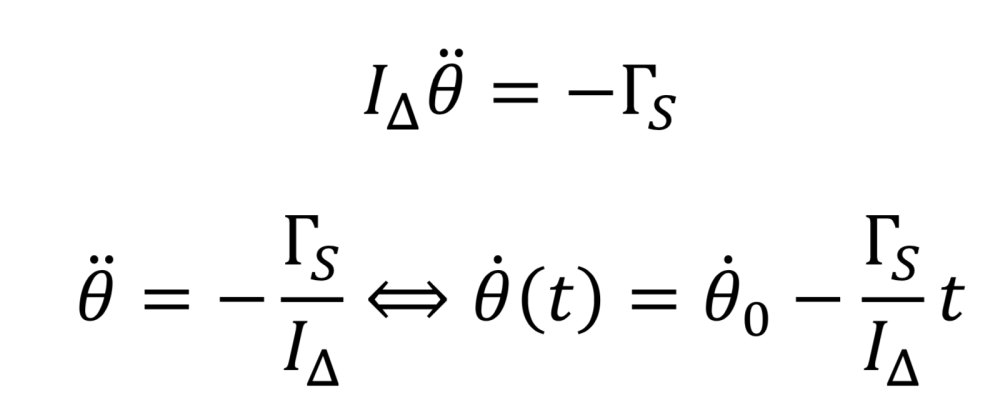
b) Étude expérimentale
Pour éliminer les frottements fluides, nous avons mesuré l’évolution de la vitesse de rotation du hand spinner sous une cloche à vide. Nous avons toutefois voulu vérifier que le vide était de bonne qualité en mesurant la pression et la température. En assimilant l’air à un gaz parfait, nous savons que :
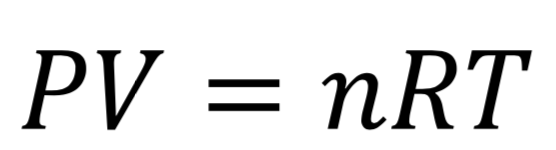
Ainsi, alors que la température de la salle est égale à 23°C au moment de l’expérience, et que la pression est égale à 1011 hPa, cela donne une densité molaire dans la salle égale à :
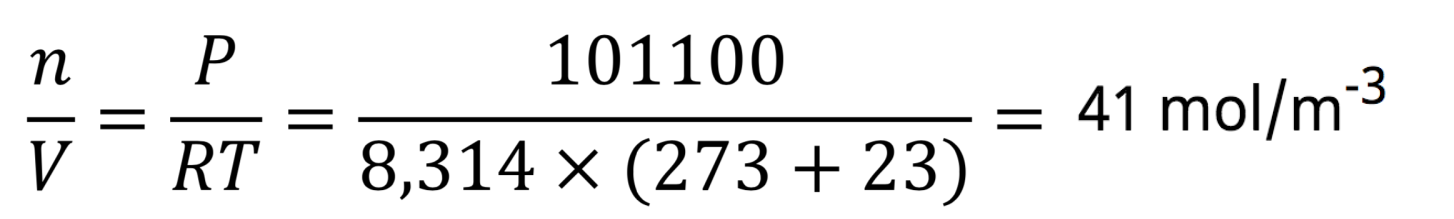
Après avoir fait le vide dans la cloche, la température vaut 19°C et la pression vaut 15 hPa. Cela donne une densité molaire de 0,62 mol/m3. Même si on est loin du vide, la diminution de la densité particulaire nous semble suffisamment significative pour aller jusqu’au bout de notre expérience.
La difficulté a été de trouver un moyen de déclencher la rotation du hand spinner une fois le vide réalisé dans la cloche. Après plusieurs essais de protocoles peu productifs, nous avons fini par trouver un moyen très efficace, figure 9.
L’idée est de maintenir le hand spinner immobile à l’aide de 2 élastiques tendus. Un des élastiques est fixé en haut, tandis que l’autre est fixé en bas. Grâce à une corde de guitare, il est possible de tirer sur l’élastique du bas. Le hand spinner n’étant plus retenu vers le bas ; l’élastique du haut le tire violement vers le haut, provoquant la rotation rapide du hand spinner. Tout ceci se passe sous la cloche à vide, et la corde de guitare peut passer sous la cloche à vide sans gêner l’étanchéité.
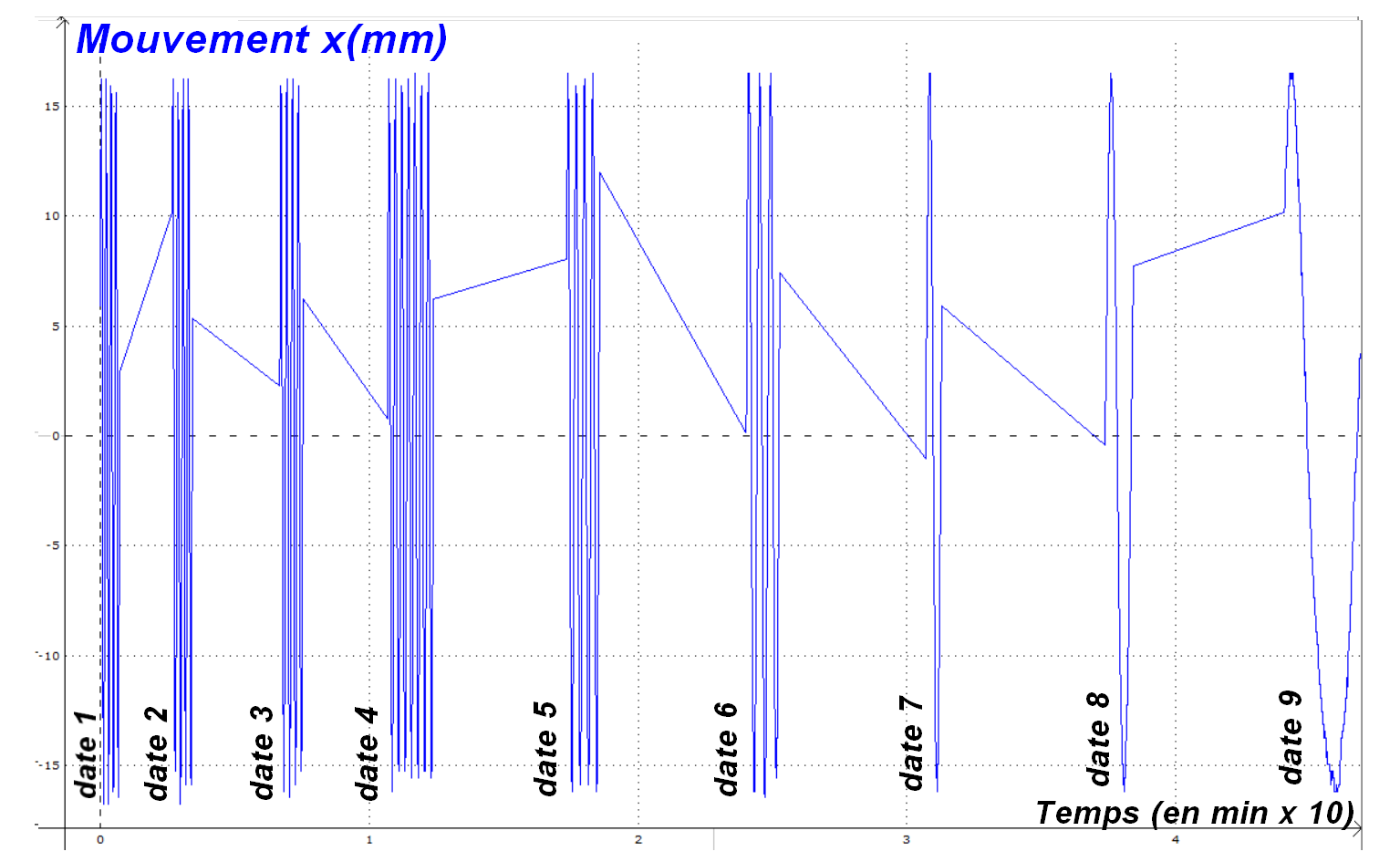
Nous avons filmé la rotation du hand spinner à 240 images par seconde et mesuré sa vitesse de rotation au cours du temps. L’exploitation a été réalisée à l’aide du logiciel Latis pro. À partir de la vidéo réalisée, nous avons mesuré la vitesse de rotation du hand spinner à 9 dates différentes durant sa rotation. Pour mesurer cette vitesse à chacune des dates en question, nous avons défini un repère et nous avons noté les coordonnées spatiales d’une des branches au cours du temps. On peut par exemple tracer l’évolution d’une de ces coordonnées pendant des durées courtes prises à différentes dates, figure10.
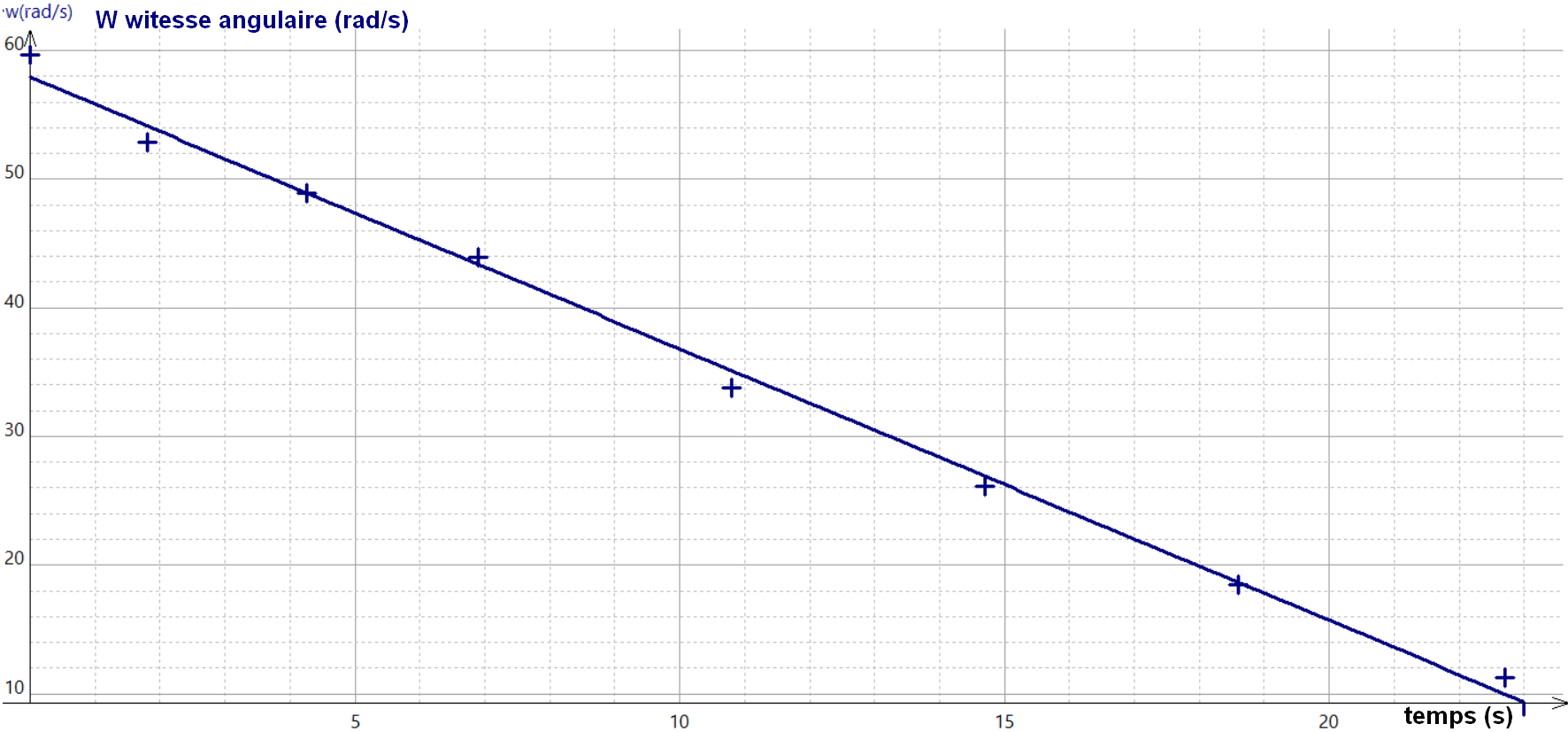
On peut en déduire la période puis la fréquence de rotation du hand spinner (en tenant compte du fait que l'étude de la vidéo a été réalisée sur la vidéo ralentie 10 fois). En multipliant ensuite la fréquence par 2π, on aboutit à la vitesse angulaire du hand spinner à certaines dates. Nous avons alors tracé l’évolution de cette vitesse sur Regressi et nous obtenons le graphique, figure 11.
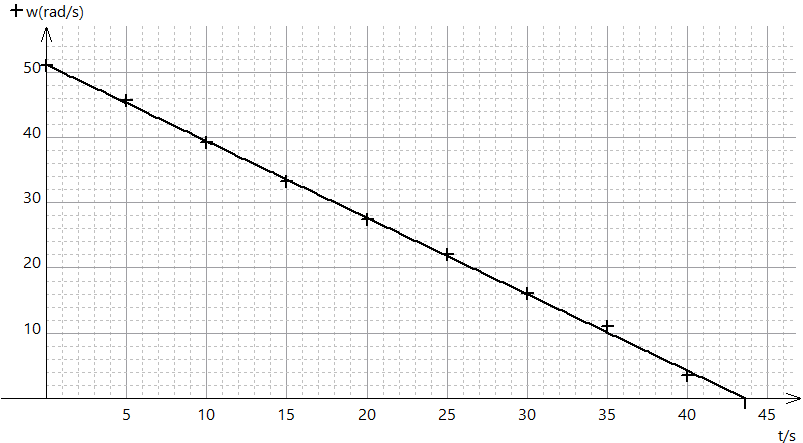
On obtient bien une droite, comme nous l’espérions. Les résultats sont alors cohérents avec un modèle de force de frottements solides indépendant de la vitesse de rotation du hand spinner.
On obtient un couple de frottements solides :
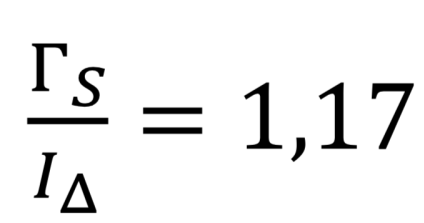
Doù ![]() = 6,64.10-4 Nm
au lieu de 1,15 Nm obtenus précédemment.
= 6,64.10-4 Nm
au lieu de 1,15 Nm obtenus précédemment.
Nous reviendrons sur cette différence plus loin partie 4.3.
Avant d’en arriver là, nous nous sommes posés la question de savoir où se situaient les frottements. Il doit s’agir de frottements entre les billes et la couronne en plastique qui maintient les billes. On peut toutefois se demander si à grande vitesse, les billes arrivent à tourner aussi rapidement que la couronne extérieure, ou alors, est ce qu’il n’y aurait pas un glissement d’une partie sur une autre ?
4. Quels autres phénomènes peuvent affecter la vitesse de rotation du hand spinner ?
4.1 Est-ce que l'axe de rotation de la bille reste le même au cours de la rotation du hand spinner ?
Pour répondre à cette question, nous avons déssiné un point sur toutes les billes du roulement (figure 12) et nous avons voulu savoir si ces points restaient visibles au cours de la rotation du hand spinner.
Figure 12. Marquage des billes du roulement |
Notre enregistrement nous a permis de constater que l’axe de rotation des billes ne reste pas perpendiculaire au plan du hand spinner puisque tous les points disparaissent du champ de vision après quelques rotations.
4.2 Y a-t-il un roulement avec glissement, ou bien le roulement est parfait ?
a) Par quel moyen va-t-on pouvoir mesurer un éventuel glissement ?
Pour avoir accès à un éventuel glissement, nous avons voulu comparer la vitesse de rotation du centre d’inertie d’une bille par rapport à celle d’une branche du hand spinner, pour ensuite déterminer si la bille ne fait que rouler ou si elle glisse également. Pour cela, nous avons cette fois travaillé avec 2 faisceaux Laser (figure 13). Le premier, en étant occulté périodiquement par les branches du hand spinner, permet de d'avoir une mesure de l’angle de rotation des branches. Le deuxième faisceau passe dans le roulement lui-même et est alors occulté à chaque fois qu’une bille passe sur son trajet.
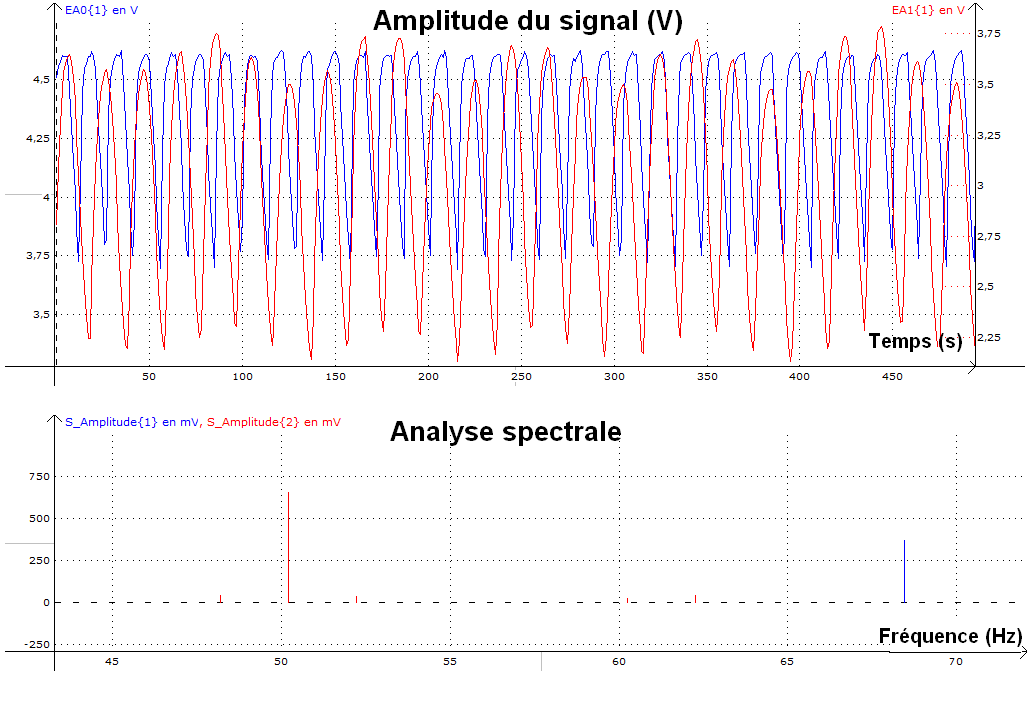
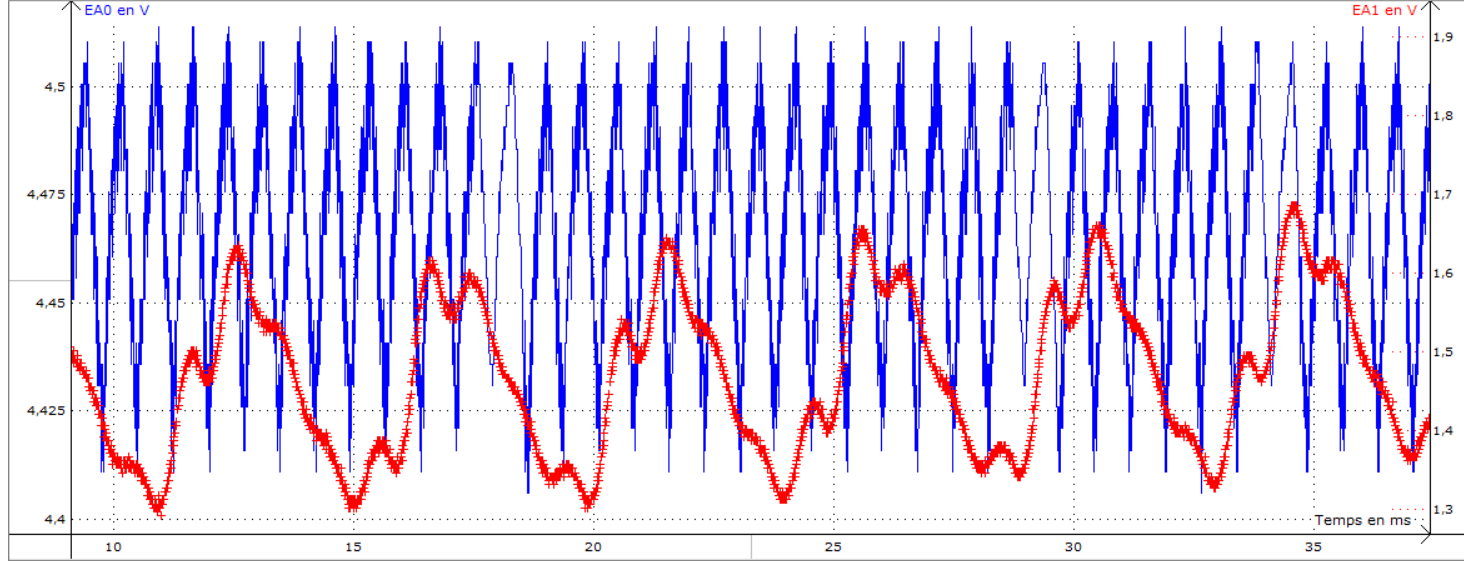
Sur la figure 14, nous présentons le résultat d’une acquisition de 0,5 s durant la rotation du hand spinner. La courbe bleue représente le signal lié au passage des branches du hand spinner, alors que le signal en rouge représente le signal lié au passage des billes.
En reprenant la méthode précédente pour en déduire la vitesse de rotation, nous obtenons :
Pour la couronne extérieure (6 branches) :
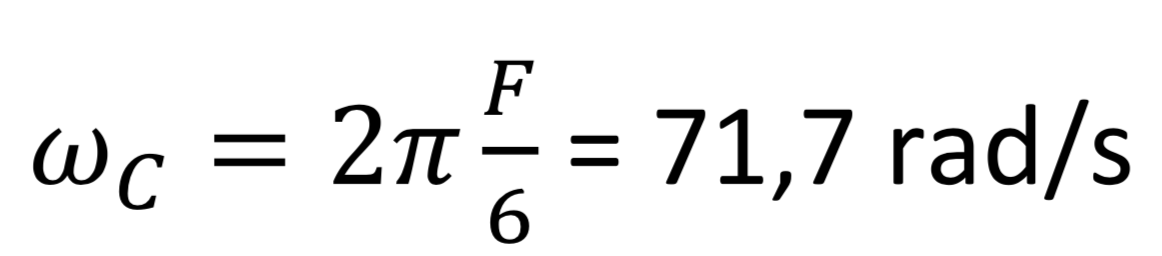
Pour les 7 billes :
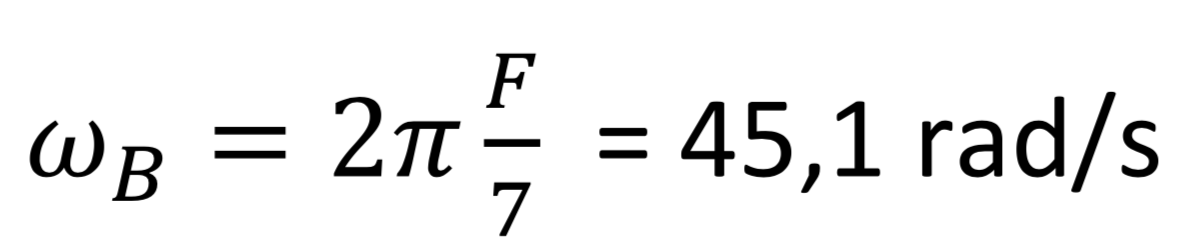
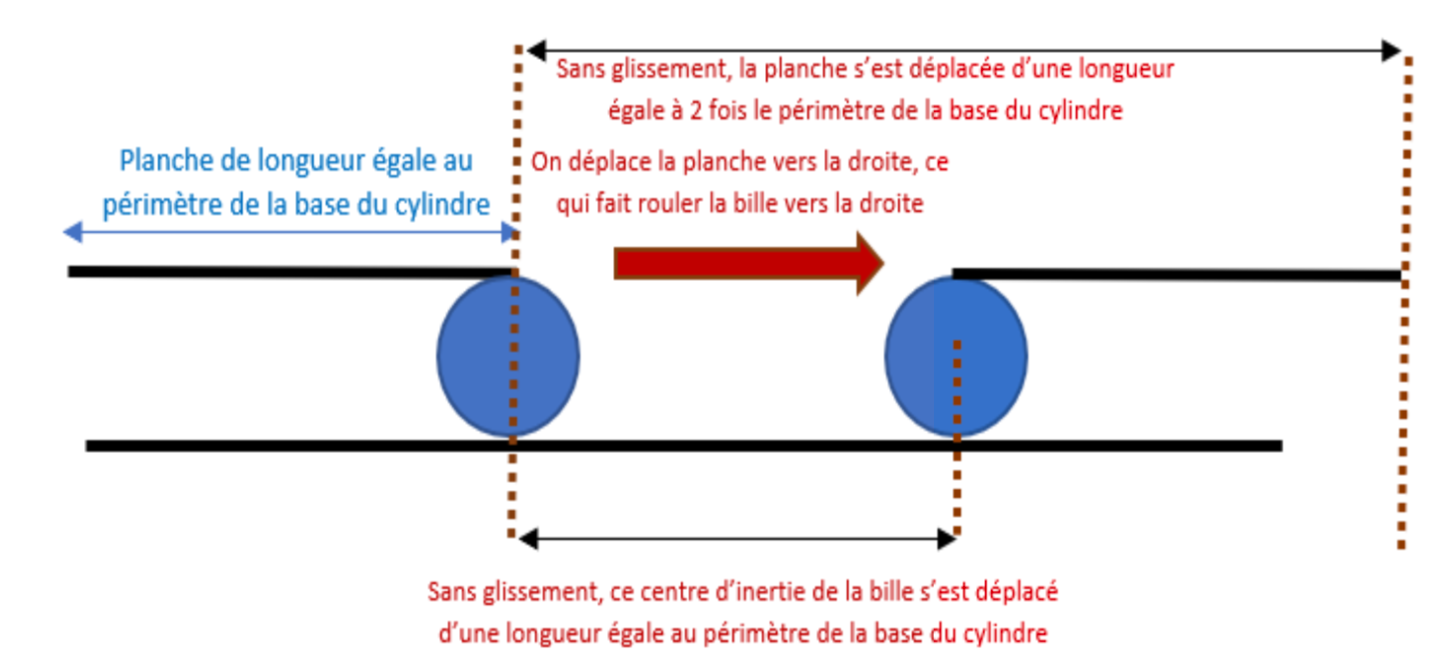
Le fait que les deux vitesses de rotation soient différentes n’est pas dû à un phénomène de glissement. Pour nous en convaincre, nous avons pris une planche que nous avons posé sur un cylindre (figure 15). Nous avons alors déplacé la planche en la faisant rouler sur le cylindre, ce qui provoquait le déplacement par roulement du cylindre par rapport à la table. On constate bien alors que la planche se déplace plus que l’axe de rotation du cylindre par rapport à la table. On visualise également bien le fait que s’il n’y a pas de glissement d’une partie sur une autre dans cette expérience : la planche se déplace de la même quantité par rapport à la verticale passant par le centre d’inertie du cylindre, que le point de contact entre le cylindre et la table par rapport à la table.
Ainsi, dans le cas du hand spinner, pour savoir si les vitesses angulaires mesurées témoignent d’un roulement avec ou sans glissement, nous devons trouver la relation entre la vitesse angulaire des branches et la vitesse angulaire du centre de gravité des billes dans l’hypothèse de roulement sans glissement.
b) Quelle est la relation théorique entre les vitesses de rotation des branches et des centres de gravité des billes ?
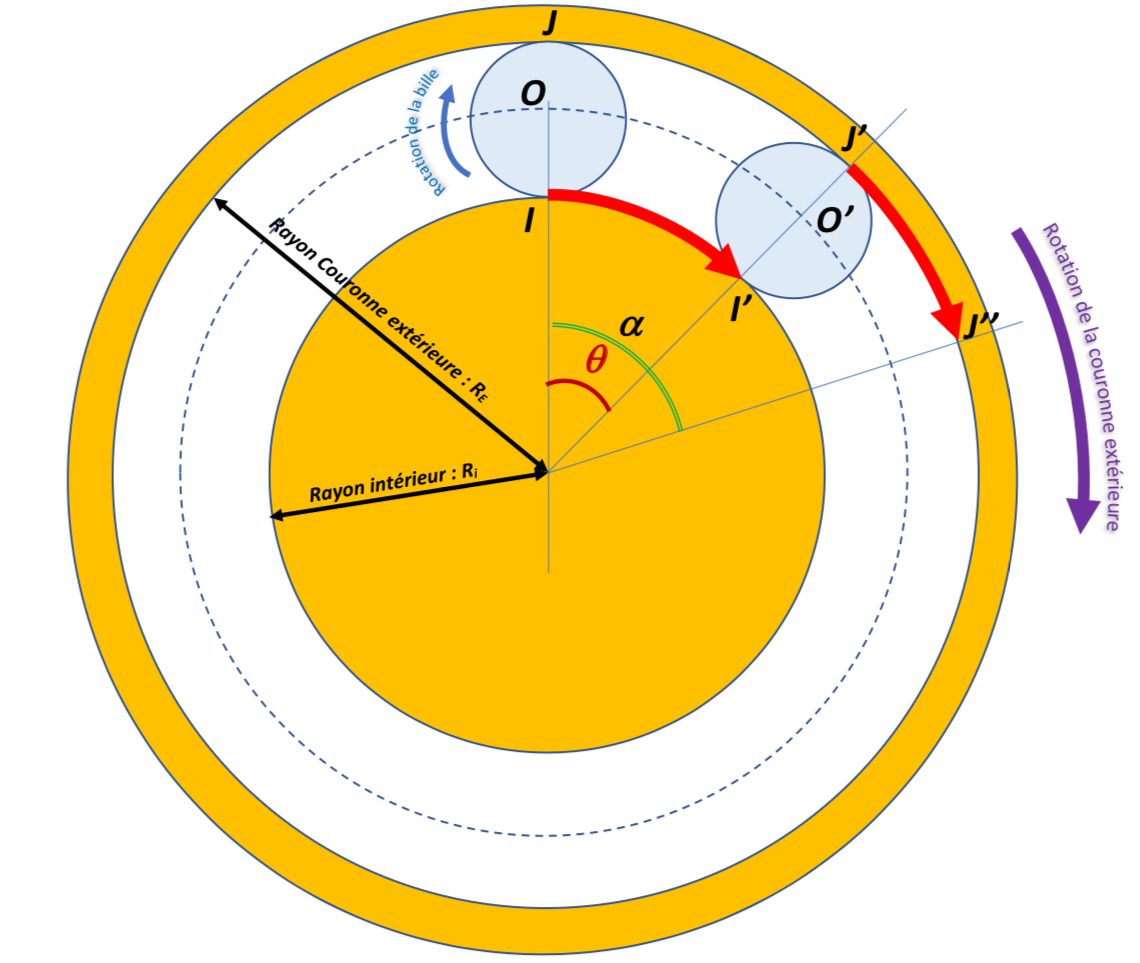
Si l'on raisonne de la même manière que précédemment, on peut affirmer que lorsque la couronne extérieure tourne, elle fait rouler la bille sur le cercle intérieur, figure 16. On se place dans le cas où il n’y a pas de glissements d’une surface sur une autre. Lorsque le centre d’inertie de la bille passe de O à O', le point de contact entre la bille et le disque intérieur passe de I à I’. Le point de contact a alors parcouru une distance :
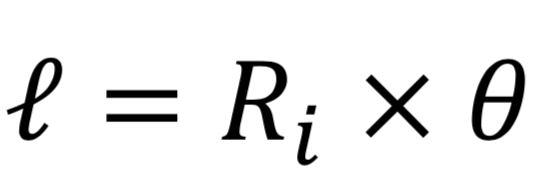
Et le point de contact entre la bille et la couronne extérieure passe de J à J' en parcourant la distance :
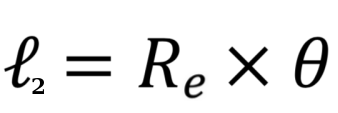
Pendant ce déplacement de la bille, le point de contact J entre la bille et la couronne extérieure s’est alors déplacé de la même distance par rapport à la bille. Autrement dit, l’arc de cercle entre J’ et J’’ mesure également :
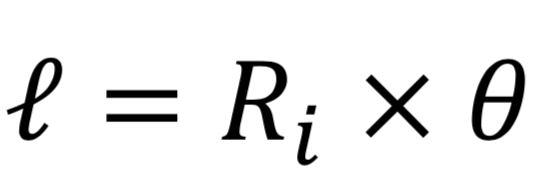
Finalement, lorsque le centre d’inertie de la bille passe de O a O’, il tourne d’un angle θ, et pendant ce même déplacement, la couronne extérieure tourne d’un angle :
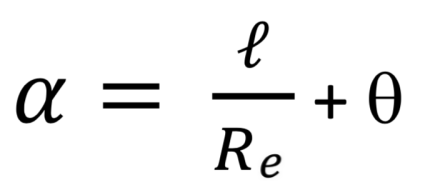
Donc :
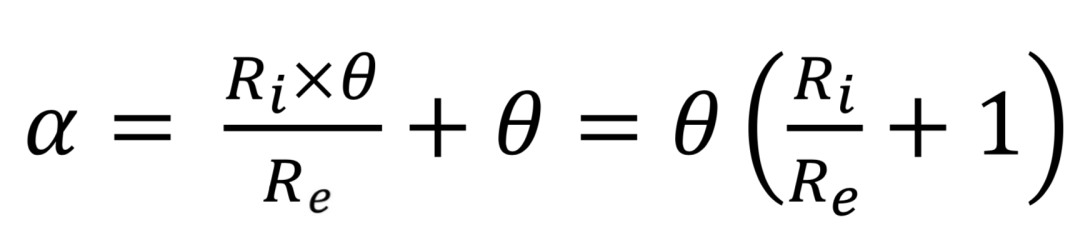
Comme ces déplacements se font durant le même laps de temps, les vitesses
angulaires ![]() et
et ![]() correspondantes sont reliées par la relation suivante :
correspondantes sont reliées par la relation suivante :
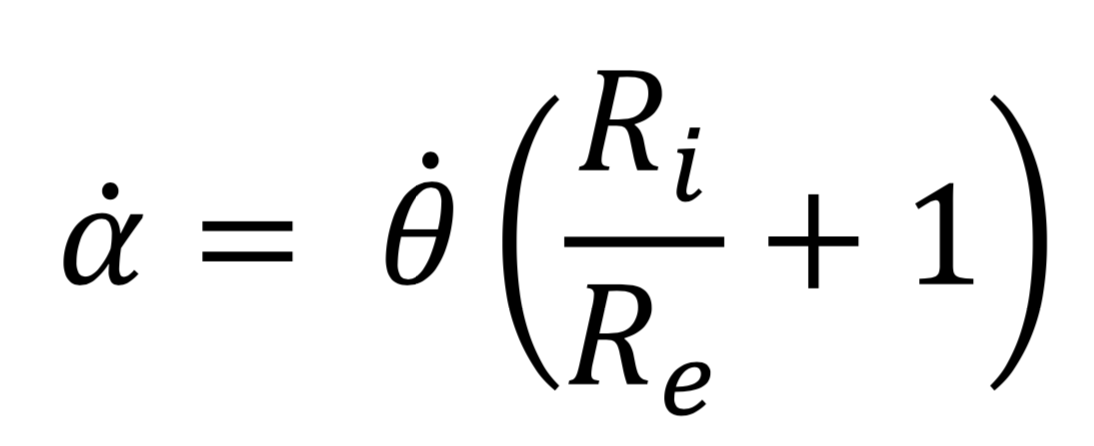
Comme nous connaissons Ri et Re, nous pouvons réaliser ce calcul.
En notant alors 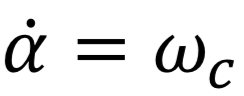 la vitesse angulaire des branches du hand spinner et
la vitesse angulaire des branches du hand spinner et
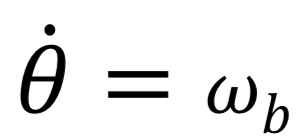 la vitesse angulaire des centres de gracité des billes,
la vitesse angulaire des centres de gracité des billes,
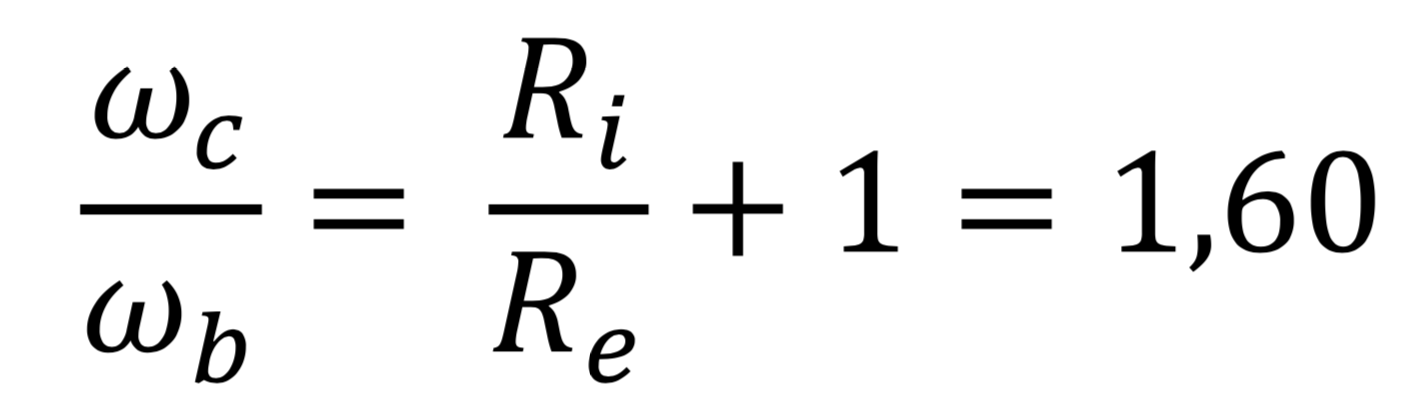
La question est de savoir si la valeur de ce rapport, obtenu simplement de façon théorique en tenant compte des géométries des éléments concernés, peut être confirmé expérimentalement. Et une autre question est de savoir si la valeur du rapport de ces vitesses mesurées expérimentalement est constante quelle que soit la vitesse de rotation de la couronne.
Répondons maintenant à ces questions de façon expérimentale.
c) Mesures expérimentales
Nous pouvons déjà répondre à la première question, à savoir si la valeur du rapport des vitesses angulaires calculé théoriquement est cohérente avec la mesure expérimentale réalisée au 1.
Nous avions trouvé ωc = 71,7 rad/s et ωb = 45,1 rad/s.
Le rapport donne alors :
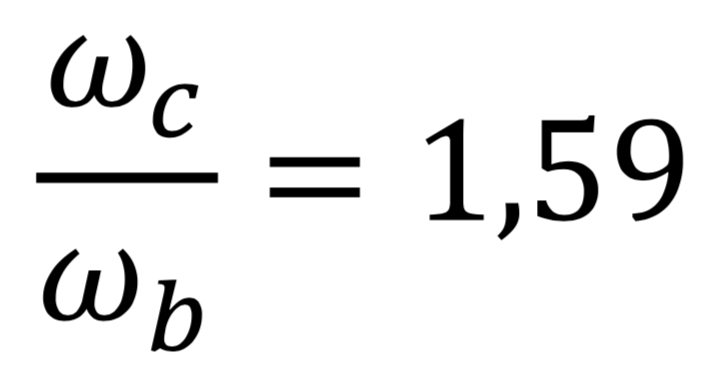
Lorsque nous comparons cette valeur à la valeur théorique (1,60) obtenue dans l’hypothèse d’absence de glissement, nous pourrions penser que cette hypothèse est confirmée. Avant d'estimer les incertitudes de mesure et de chercher à interpréter ce léger écart, nous avons voulu voir si ce rapport pouvait dépendre de la vitesse de rotation du hand spinner.
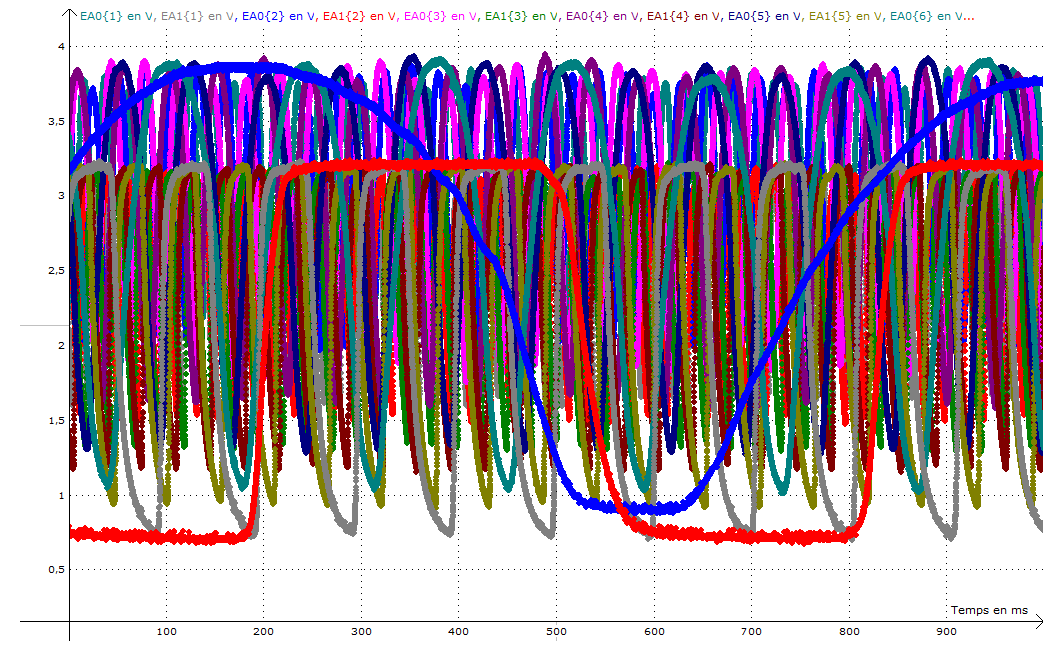
Nous avons alors fait tourner à la main le hand spinner, aussi vite que nous le pouvions. Durant sa rotation, nous avons réalisé des acquisitions de 1 seconde, toutes les 5 secondes.
Nous obtenons un ensemble de paires de signaux (ceux issus du faisceau obturé par les branches, et ceux issus du faisceau obturé par les billes) qui nous ont permis de déterminer les vitesses angulaires :
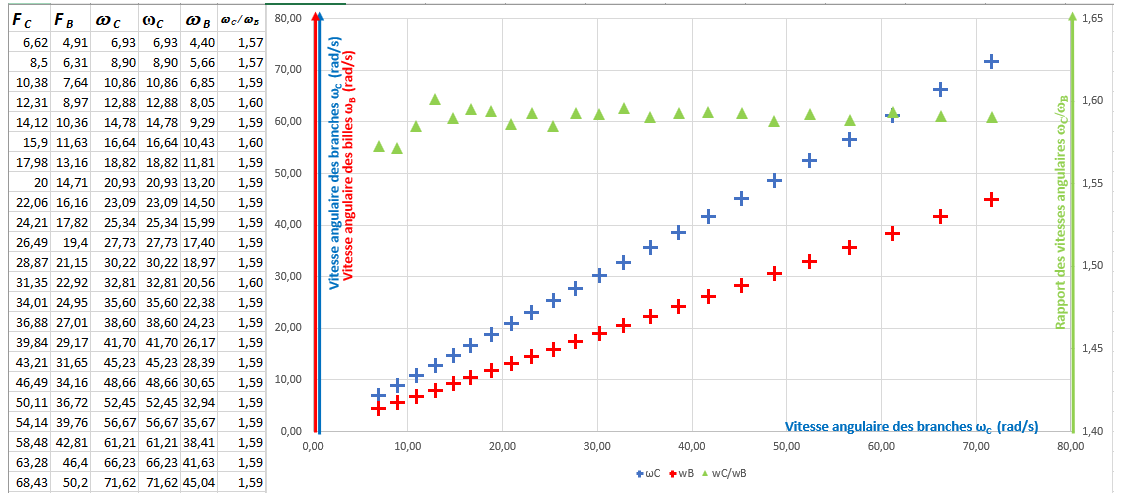
La figure 18 présente en bleu, la vitesse de rotation des branches, en rouge, celle des centres d’inertie des billes et la courbe verte montre le rapport respectif de ces deux vitesses. On constate que ce rapport reste globalement constant quelle que soit la vitesse de rotation du hand spinner et confirme la valeur que nous avons obtenue dans le paragraphe précédent. Les 2 premières valeurs de ce rapport, sont moins précises, puisqu’établies à partir d’un très faible nombre de périodes affichées.
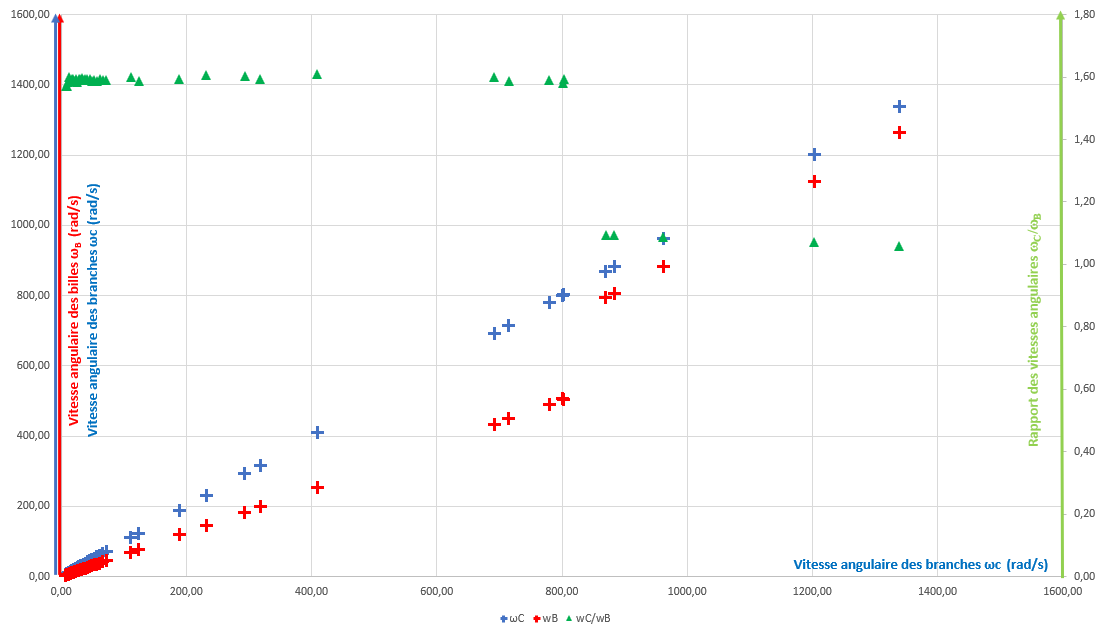
Il nous a paru tout de même étrange que le rapport des vitesses angulaires ne dépende pas du tout de la vitesse de rotation. Nous avons alors voulu savoir si cela restait toujours le cas en augmentant la vitesse de rotation du hand spinner. Pour cela, au lieu de faire tourner le hand spinner à la main, nous avons soufflé de l’air comprimé dessus. L’avantage de cette méthode est que, en choisissant un débit d’air, on fixe une vitesse de rotation constante du hand spinner, ce qui rend alors plus juste la mesure des vitesses de rotation. Grâce au compresseur, nous avons pu faire tourner le hand spinner jusqu’à une vitesse de 1340 rad/s ! Soit environ 213 tours par seconde ! Les résultats obtenus sont présentés dans la figure 19.
On voit nettement que pour une vitesse de 800 rad/s, la vitesse de rotation des billes suit celle des branches du hand spinner. Ce décrochage est vraiment spectaculaire. Et plus on augmente la vitesse des branches, plus le rapport tend vers 1, ce qui signifie que le centre d’inertie des billes tourne alors pratiquement avec la même vitesse de rotation que celle des branches. Autrement dit, les billes ne semblent plus rouler, mais glisser !
Comment expliquer cela ? Car même si nous nous attendions à ce qu’il y ait un glissement pour une vitesse donnée, on ne pensait pas qu’il serait aussi brutal. Au lieu d’avoir un phénomène progressif, il semble y avoir une limite très nette au-delà de laquelle quelque chose de particulier se passe. Mais quel est ce phénomène ?
À la vue des résultats expérimentaux, on pourrait dire que si les billes tournent à la même vitesse de rotation que celle des branches, c’est qu’elles ne sont pratiquement plus en contact avec l’anneau central du roulement à billes. Et les billes seraient alors pratiquement collées à la couronne extérieure du hand spinner. Comment cela est possible ? Est-il possible que la température s’élève dans le roulement, et que la dilatation des matériaux soit à l’origine de la modification des contacts entre les billes et les différentes parties du hand spinner ? Et concernant le fait que les billes restent collées à la couronne extérieure du hand spinner, se peut-il que ce soit dû à un effet centrifuge ? Ou alors y a-t-il des phénomènes liés à la pression ? Dans la partie 5, nous allons essayer de répondre à ces questions, et en même temps, de voir ou de comprendre les solutions qui permettent de repousser les limites de la vitesse du roulement à billes. En effet, c’est en cherchant à repousser cette limite que des hypothèses pour expliquer son origine nous sont venues. Mais avant cela, voyons un troisième point qui affecte la vitesse de rotation du hand spinner :
4.3 Effet de charge
Nous avons été confrontés à quelque chose qui affecte le roulement du hand spinner, alors que nous cherchions à faire totalement autre chose. En effet, quand nous avons vu qu’il était possible de faire tourner le hand spinner dans la cloche à vide, nous avons eu l’idée de profiter de l’absence des frottements fluides pour mesurer le moment d’inertie par une autre méthode que celle présentée dans ce mémoire.
L’idée est la suivante : Le moment d’inertie peut être vu comme la somme du moment d’inertie J1 de chacune des branches du hand spinner, ajouté à celui J0 de la couronne du hand spinner. Le moment d’inertie total du hand spinner est :
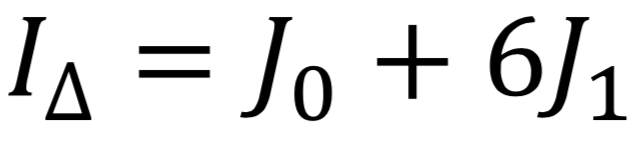
Comme nous l’avons vu, nous savons que dans la cloche à vide :
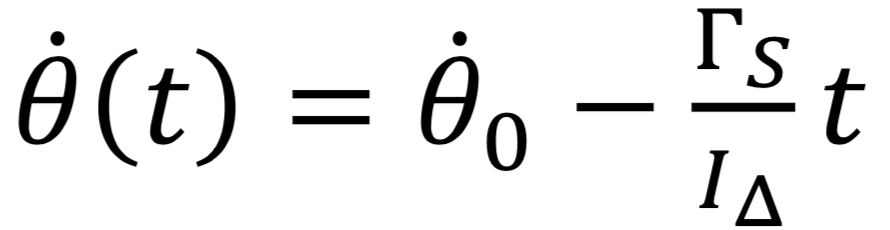
Cela correspond à une droite de coefficient directeur (en valeur absolue) :
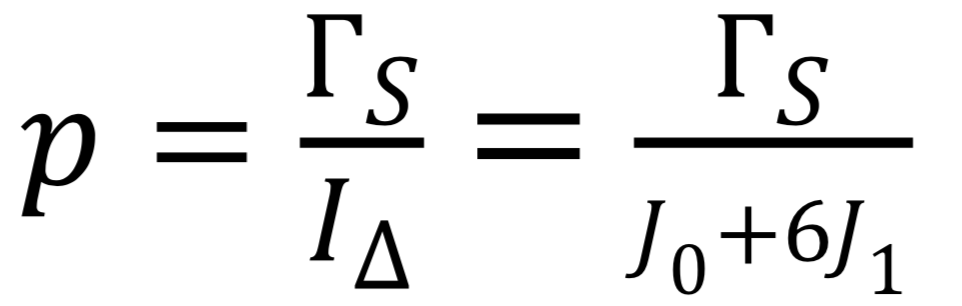
Si on réalise la même étude, en enlevant 3 branches du hand spinner, on devrait obtenir une droite de coefficient directeur (toujours en valeur absolue) :
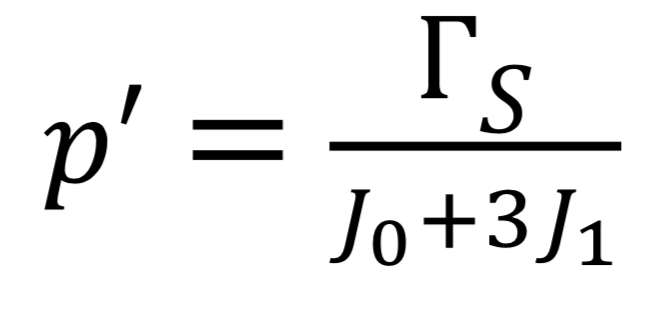
On en déduirait alors que
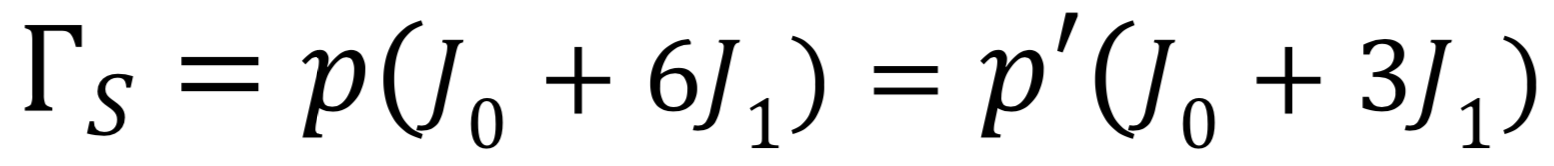
Ainsi,
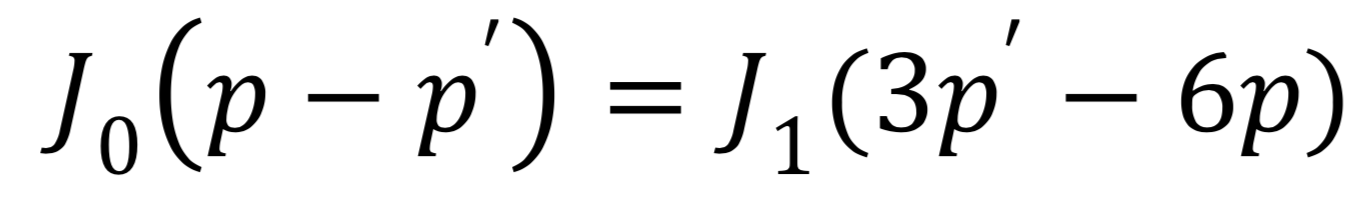
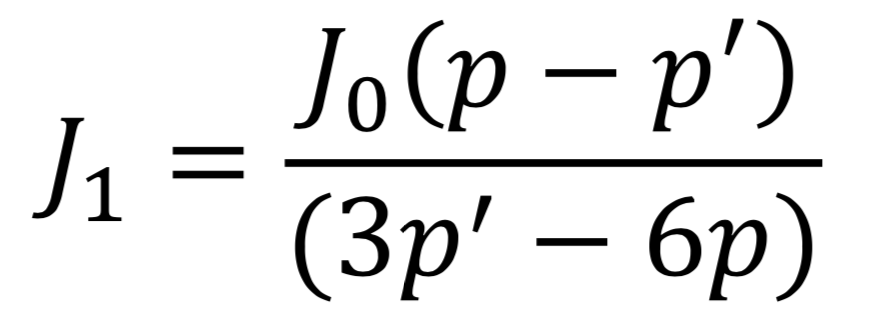
Les pentes p et p' sont déterminées expérimentalement, alors que le moment d’inertie J0 peut se calculer facilement car la partie centrale du hand spinner peut être décomposée en formes simples (un cylindre creux et un disque creux), pour lesquelles des formules existent. Par exemple pour le cylindre creux :
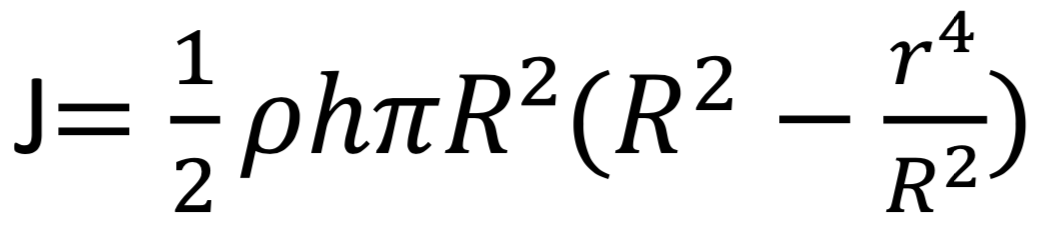
dans laquelle R est le rayon externe du cylindre creux, r son rayon interne, h sa hauteur et ρ la masse volumique de l’acier.
On trouve alors, J0 = 5,86.10-6 kg.m-2.
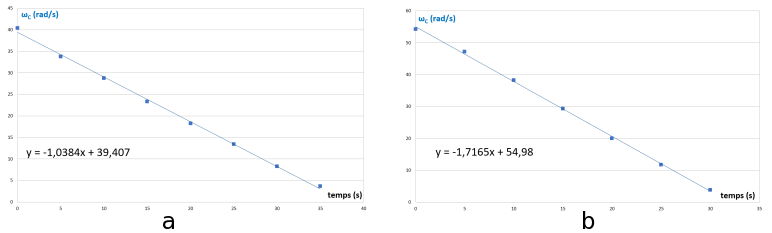
Faisons alors tourner le hand spinner avec uniquement 3 branches dans la cloche à vide et traçons l’évolution de sa vitesse de rotation au cours du temps, figure 20 :
- Avec 3 branches, on trouve une pente p' = 1,0384 rad/s
- Avec 6 branches, on trouve une pente p = 1,7165 rad/s
Comme ces résultats allaient à l’encontre de ce qui était prévu, nous avons refait les mesures... et nous avons obtenu à nouveau les mêmes valeurs...
Et c’est là que le problème arrive ! Compte tenu du fait que la pente de la droite est inversement proportionnelle au moment d’inertie
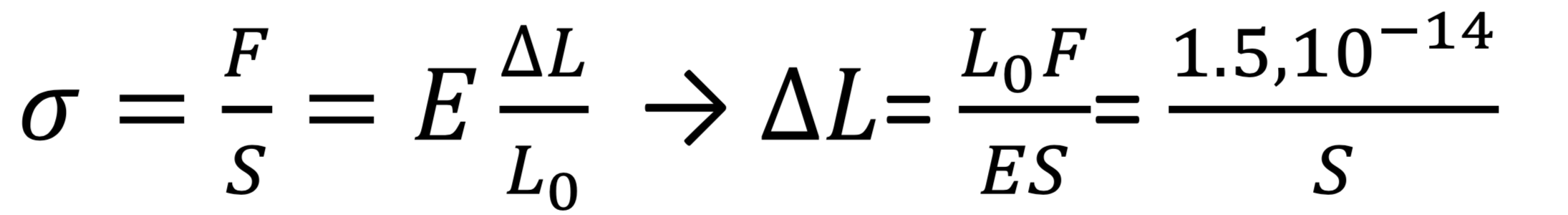
On devrait avoir p’ > p. Or ce n’est pas le cas.
Cela ne peut s’expliquer que si en réalité, le couple de force de frottement
solide ![]() dépend lui aussi du nombre de branches. Cela paraît finalement
très probable, puisque le hand spinner pèse sur le roulement, et cette force qui se
répartit sur le roulement modifie les contraintes selon la masse du hand spinner.
dépend lui aussi du nombre de branches. Cela paraît finalement
très probable, puisque le hand spinner pèse sur le roulement, et cette force qui se
répartit sur le roulement modifie les contraintes selon la masse du hand spinner.
Pour vérifier cette hypothèse, nous avons réalisé les mêmes mesures, mais en
disposant cette fois-ci le hand spinner de sorte qu’il tourne autour d’un axe
vertical et non plus horizontal. Nous obtenons alors les nouvelles pentes :
p’ = 1,03 et p = 1,14. On voit bien alors que, puisque les
pentes changent par rapport aux mesures précédentes alors que les moments d’inertie
non, c’est que ![]() est là encore modifié, car la force de pesanteur engendre des
contraintes différentes dans cette nouvelle disposition du hand spinner par rapport
à la situation précédente. On voit par ailleurs que la pente obtenue pour 6 branches
est là encore plus élevée que celle obtenue pour 3 branches.
est là encore modifié, car la force de pesanteur engendre des
contraintes différentes dans cette nouvelle disposition du hand spinner par rapport
à la situation précédente. On voit par ailleurs que la pente obtenue pour 6 branches
est là encore plus élevée que celle obtenue pour 3 branches.
On en conclut ici que bien qu’une masse importante puisse s’avérer intéressante pour que le hand spinner tourne rapidement, cette masse va engendrer des frottements solides plus importants, freinant alors davantage le hand spinner. Cela constitue donc un élément important de cet instrument. Nous avons effectué quelques recherches suite à cette réflexion, et il s’avère, effectivement, que la performance d’un roulement à bille dépendra de la « charge » que ce roulement aura à supporter, et de la façon dont cette charge se répartira sur le roulement.
Revenons alors à nos questionnements sur le rapport des vitesses angulaires des branches et des billes. Nous pensions que le moment d’inertie n’avait pas été mesuré avec une précision suffisante. Mais en réalité, lorsque nous avons réalisé la mesure de l’évolution de la vitesse du hand spinner dans l’air, le hand spinner tournait dans un plan horizontal, alors qu’il tournait dans un plan vertical dans la cloche à vide. Le couple de frottements solides n’étant pas le même, il était alors tout à fait normal que nous ne trouvions pas des résultats similaires.
5. Comment repousser la limite de vitesse de rotation du roulement à bille ?
5.1 En changeant de matériaux dans le roulement ?
Nous avons pu voir, au cours de notre travail, qu’il existe différents roulements à billes, avec différents matériaux. Par exemple, on trouve des roulements en céramique, qui sont en général qualifiés de haute performance. Nous avons alors voulu le constater en cherchant la vitesse limite atteinte par le hand spinner dans lequel on a remplacé le roulement avec les billes en acier par celui avec des billes en céramique. Nous avons fait tourner le hand spinner à des vitesses vraiment très grandes, comme en témoigne l’acquisition ci-contre, figure 21 :
La courbe bleue représente la rotation des branches, tandis que la courbe rouge celle des billes. Sur la courbe rouge, il ne faut pas tenir compte de la composante basse fréquence, qui correspond à une légère précession de l’axe de rotation du hand spinner probablement engendrée par le souffle intense de l’air comprimé.
Une lecture des fréquences de ces deux signaux conduit alors à un rapport des vitesses de rotation encore égal à 1,59 !
Nous avons pu faire tourner le hand spinner jusqu’à 225 tours par seconde sans atteindre de limite !
La céramique permet donc effectivement d’atteindre des performances bien plus importantes que celles obtenues avec des billes en acier.
Comment alors expliquer le décrochage avec les billes en acier, et que ce décrochage ne soit pas observé, ou qu’il existe peut-être pour des vitesses plus vertigineuses ?
Hypothèse d’une élévation de température :
Plusieurs idées nous sont venues. La première a été de faire l’hypothèse que lorsque le hand spinner tourne à de telles vitesses, il doit s’échauffer et les matériaux doivent alors se dilater. Cette dilatation serait responsable du fait que les billes ne se trouveraient plus en contact avec l’anneau central du roulement à bille. Et du fait de l’effet centrifuge, les billes se retrouveraient alors plaquées sur l’anneau externe du roulement, ce qui les ferait tourner pratiquement à la même vitesse de rotation que celle des branches ?
Pour savoir si une dilatation est à l’origine du décrochage observé avec les billes en acier, nous avons fait chauffer le hand spinner à une température de 50°C. Nous l’avons ensuite fait tourner à différentes vitesses, mais le décrochage observé se fait toujours autour de 800 rad/s. La dilatation ne semble donc pas intervenir dans le phénomène de décrochage. Nous pouvons d'autant plus l’affirmer qu’en chauffant le hand spinner à 50°C, sa température est bien plus importante que celle à laquelle il se trouve après une rotation à très grande vitesse.
Un autre argument qui semble témoigner dans le fait que la dilatation n’est pas le coupable recherché se trouve dans la céramique : il se trouve que le coefficient d’expansion thermique de l’acier est 76% fois plus important que celui de la céramique, comme en témoigne le tableau ci-dessous. Donc même s’il y avait une dilatation, la céramique, en gardant ses dimensions, serait encore moins en contact avec l’anneau interne du roulement que ne le sont les billes en acier.
Propriété d'une bille | Acier | Céramique (Cerbec) | Comparaison |
Densité | 7,6 | 3,2 | -58%, la céramique est plus légère |
Dureté | 700 | 1 550 | +121%, la céramique est plus dur |
Élasticité | 190 | 320 | +68%, la céramique est plus rigide |
Coefficient d'expansion thermique | 12,3 | 2,9 | -76% |
Température max °C | 320 | 1 000 | +680°C |
Rugosité de la surface | 0,02 | 0,005 | +75%, la céramique est plus lisse |
Hypothèse d’une déformation des matériaux à cause de contraintes mécaniques :
En observant ce tableau, on remarque aussi que les billes en céramique sont 68% plus rigides que les billes en acier. Peut-être alors que, du fait de la très grande vitesse de rotation, il y a une déformation des matériaux : les billes en acier perdraient alors leur sphéricité, et ne seraient plus en contact avec l’anneau central, contrairement aux billes en céramique. Connaissant le module d’élasticité de l’acier, nous avons voulu évaluer l’ordre de grandeur de la déformation de la bille compte tenu de la contrainte subie par la bille lors de sa rotation.
Connaissant la masse des billes, leur vitesse de rotation et le rayon de leur trajectoire, on peut évaluer la force centrifuge qu’elles subissent :
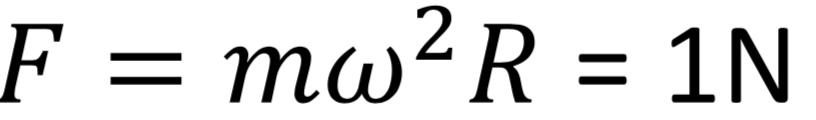
Pour les billes en acier. On peut alors dire que les billes sont plaquées contre la couronne extérieure, et subissent de la part de celle-ci une force de 1N. D’après la loi de Hook, on peut alors estimer (en supposant que la bille ne se déforme que sur une seule direction) la variation du diamètre de la bille ΔL en fonction de la surface de contact entre la bille et la couronne extérieure :
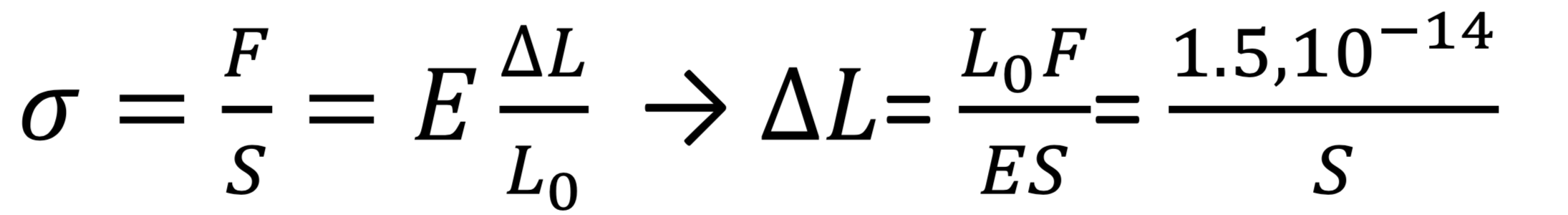
On ne peut pas connaître avec précision la surface de contact S, mais cette surface est dans tous les cas très faible, répartie sur une ou deux lignes selon les géométries de la bille et du sillon extérieur. Il n’est pas impossible que cette surface soit de l’ordre de 10-9 m2, ce qui diminuerait alors le diamètre de la bille d’environ 10 μm, diminuant alors le contact entre la bille et la couronne interne. Ce qui rejoint la troisième hypothèse dont nous parlons ensuite…
Hypothèse de la variation des forces de frottement :
D’après les lois de Coulomb pour les frottements, nous savons que les forces de frottements exercées par la couronne intérieur sur les billes sont d’autant plus grandes que la force avec laquelle la bille appuie sur cette couronne intérieure est grande. Il en est de même avec les forces de frottements entre la bille et la couronne extérieur. Ces forces de frottements permettent, rappelons-le, le roulement de la bille. Or, plus la bille tourne vite, et moins la bille appuie sur la couronne intérieure, alors que la bille appuie davantage sur la couronne extérieure. De ce fait, la force de frottements devient faible sur la couronne intérieure, et il peut alors exister une limite à sa valeur en dessous de laquelle les frottements ne sont plus suffisants. La bille ne peut alors plus rouler : elle glisse.
5.2 En lubrifiant le roulement ?
Comme nous l’avons souligné précédemment, les frottements à éliminer pour que le hand spinner tourne plus longtemps sont ceux entre les billes et la couronne en plastique qui les maintient. Les frottements des billes avec les parties métalliques sont quant à eux ceux qui permettent au hand spinner de tourner.
Nous pouvons diminuer les frottements solides en rajoutant un peu d’huile au niveau du roulement. Pour constater de façon objective l’intérêt de lubrifier le roulement à billes, nous avons comparé l’évolution de la vitesse en fonction du temps, pour le même hand spinner placé sous la cloche à vide, sans huile pour commencer, puis avec une goutte d’huile. Voici les résultats obtenus, figure 22.
Figure 22. Vitesse de rotation du hand spinner. En haut : hand spinner sans lubrifiant - en bas : hand spinner avec lubrifiant |
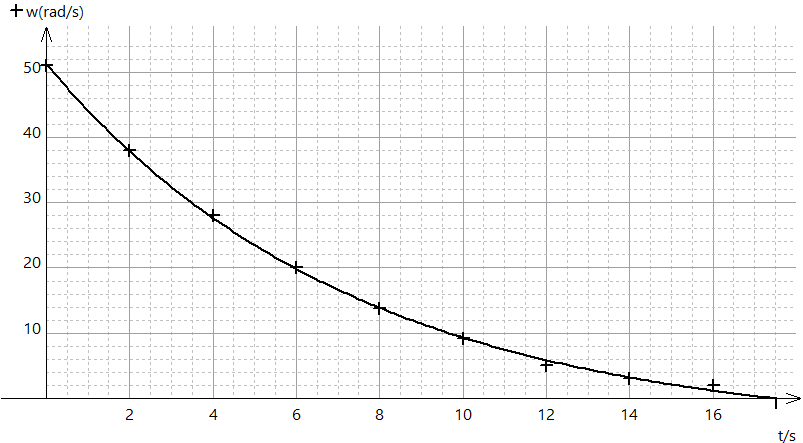
Contrairement à ce que à quoi nous nous attendions, nous constatons que le hand spinner s’arrête de tourner beaucoup plus rapidement en présence d’huile : il tourne deux fois plus longtemps sans huile qu’avec de l’huile, pour une vitesse initiale quasiment identique.
La décroissance non linéaire de la vitesse de rotation au cours du temps en présence d’huile témoigne du fait qu’en réalité, la présence d’huile a engendré des frottements fluides importants au sein même du roulement. Pour aller plus loin, nous pouvons tout de même dire que les frottements solides ont bel et bien diminué. En effet, compte tenu que l’expérience se passe dans la cloche à vide, nous avons vu que :
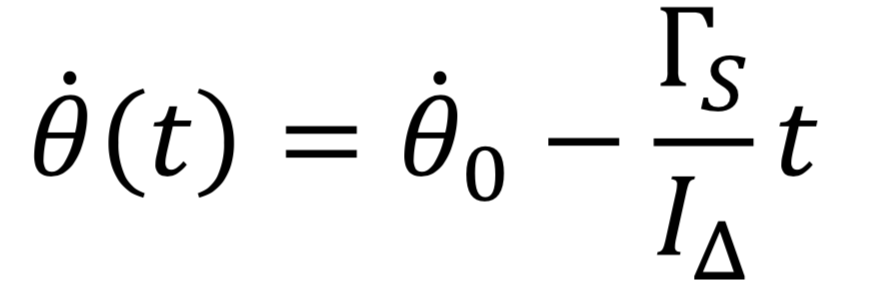
Par ailleurs, comme la courbe du bas, obtenue avec l’huile, peut-être modélisée par une fonction du type :
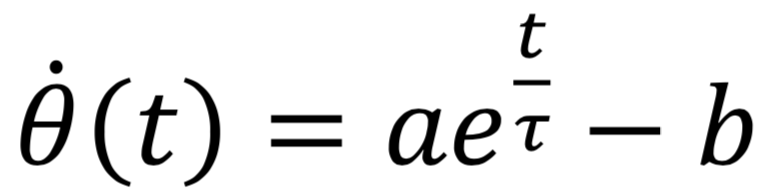
C'est-à-dire de la même forme que celle établie au 3.2 Mise en équation.
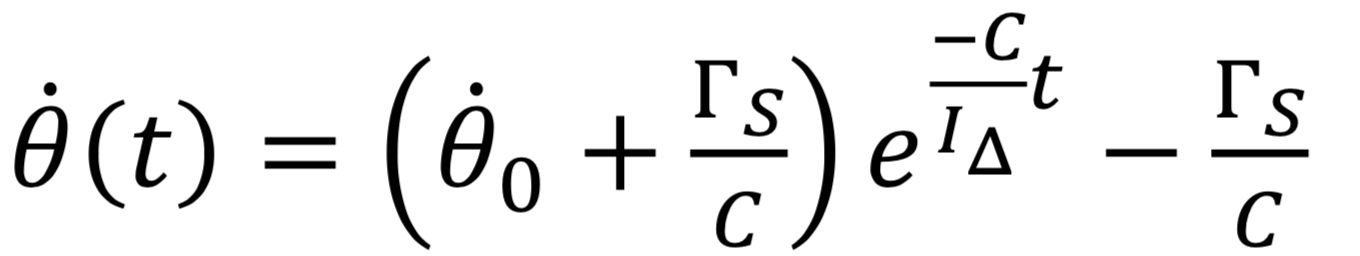
On peut supposer que l’huile est responsable d’un couple de forces de frottements proportionnel à la vitesse. Les modélisations des deux courbes sont les suivantes :
Pour la rotation du hand spinner sans huile :
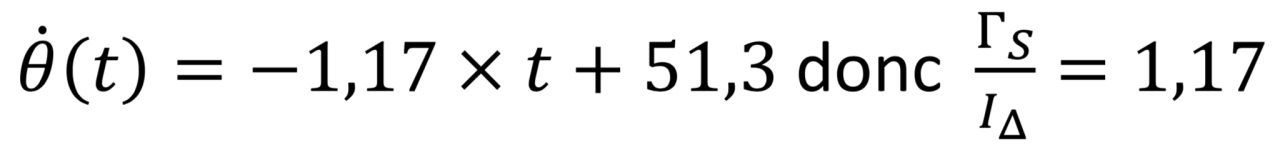
Pour la rotation du hand spinner avec huile :

Donc :
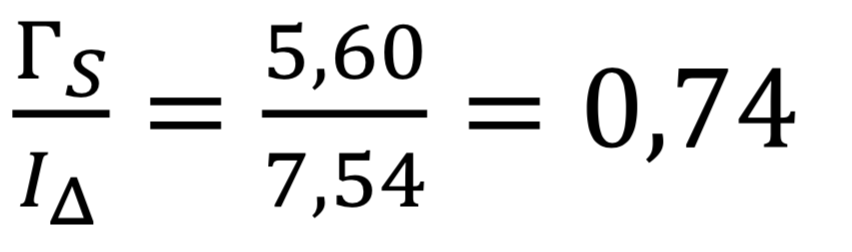
Comme le moment d'inertie I∆est une valeur qui ne change pas par ajout de l’huile, c’est donc bien que le couple de forces de frottements solides a diminué en ajoutant de l’huile. Et donc, parallèlement à cela, les frottements fluides ont augmenté, sans pouvoir être compensés par la diminution des frottements solides.
6. Conclusion
Pour choisir un hand spinner, il faut faire des compromis, car ce que l’on gagne d’un côté, on peut le perdre de l’autre. Une plus grande masse peut par exemple permettre d’avoir un moment cinétique plus important, mais conduira à une charge, donc à des frottements plus importants également. Pour éviter les frottements fluides, la forme du hand spinner ne peut pas être élaborée uniquement à partir de considérations esthétiques.
De façon plus générale, l’étude du hand spinner nous a finalement amené à comprendre le roulement à billes. Nous avons dû pour cela faire de nombreuses expériences, nous amenant souvent vers d’autres hypothèses… Il y a encore sûrement beaucoup à dire sur le sujet, mais nous avons déjà eu beaucoup de plaisir à réaliser tout ce travail, et au départ, nous étions loin d’imaginer que nous ferions toutes ces investigations. Le fait enfin d’avoir mélangé les matériaux, en utilisant par exemple la céramique nous a poussé à étudier la particularité de certains contacts, comme ceux entre l’acier et la céramique, souvent utilisés dans les prothèses. Mais ce sera pour un autre projet !
Pour citer cet article :
Hand spinner, Minault, Daugé, Guinouard, juin 2019. CultureSciences Physique - ISSN 2554-876X, https://culturesciencesphysique.ens-lyon.fr/ressource/hand-spinner.xml