Activer le mode zen
Ressource au format PDF
Mots-clés
- frottement
- moment
- rotation
- force
Classification
Observations et réflexions autour d'une bobine de fil
28/05/2003
Résumé
Cet article présente une succession d'expériences de mécanique autour d'une bobine et la façon dont on peut interpréter les résultats inattendus que l'on obtient, sans faire de calcul.
Table des matières
Où il est montré qu'une bobine de fil peut avoir en certaines circonstances un comportement apparemment paradoxal (on peut enrouler un fil autour d'une bobine en se contentant de tirer sur le fil). On recherchera la faille des raisonnements erronés et on proposera plusieurs interprétations physiques simples. Le lecteur aura intérêt à fabriquer une bobine assez lourde et dont les deux diamètres (gorge et joues) seront nettement différents. Elle devra être assez grande pour d'évidentes raisons pédagogiques. Le choix des matériaux devra favoriser un bon coefficient de frottement plan/bobine.
Facile !
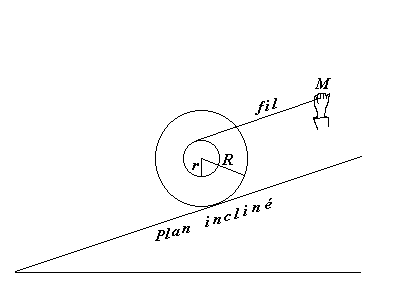
Question : la bobine peut-elle éventuellement rester à l'équilibre dans l'expérience représentée ci-dessus (extrémité M fixe) ?
Réponse : oui, pourquoi pas...
Expérience : la bobine se maintient au repos et cela n'étonne personne.
Pourquoi ce résultat paraît-il assez évident ? Parce que si la bobine descendait le plan en roulant, cette rotation conduirait à enrouler le fil, ce qui est impossible si son extrémité M est fixe.
C'est « magique » !
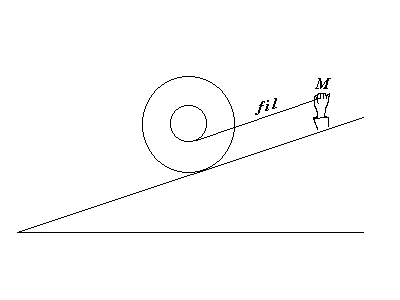
La bobine a été retournée (schéma ci-dessus).
Question : va-t'elle rester en place ?
Réponse : (quasi-unanime) ah non ! Elle va descendre !
Expérience : elle se maintient au repos au grand étonnement de la plupart.
Pourquoi cette erreur de jugement ? Parce que le même raisonnement est appliqué : rien ne devrait empêcher la bobine de dévaler la pente en déroulant le fil dont l'extrémité M est restée fixée.
Encore plus fort !
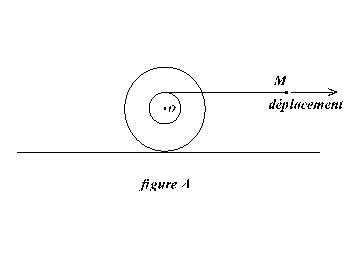 | 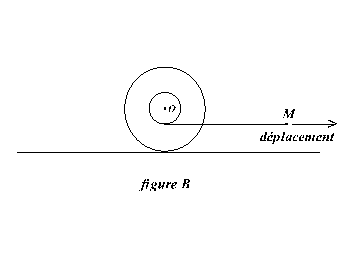 |
Le plan est maintenant horizontal et on déplace l'extrémité M du fil vers la droite.
Question : quel sera le sens de déplacement de la bobine ?
Réponse : (quasi unanime)
- vers la droite dans la configuration A ;
- vers la gauche dans la configuration B.
Expérience : vers la droite dans les deux cas. Le fil se déroule en A et s'enroule (!) en B.
Pourquoi ces réponses : Parce que chacun d'entre nous est persuadé qu'une traction sur un fil ne peut que conduire à dérouler celui-ci. D'ailleurs, le moment de la force de traction par rapport à l'axe O semble devoir la faire tourner :
- en A dans le sens horaire (ce qui est confirmé par l'expérience) ;
- en B dans le sens antihoraire (ce qui est infirmé par l'expérience).
Expérience cruciale
Essayons de voir dans quelles conditions cette bobine peut passer d'un comportement « normal » à un comportement qui apparaît « aberrant ».
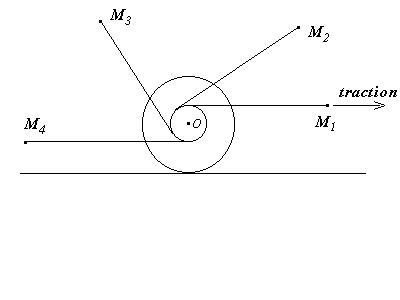
Pour cela on va tirer constamment sur le fil de façon à le faire passer de la position 1 (traction à droite → déplacement à droite) à la position 4 (traction à gauche → déplacement paradoxal à gauche). Quelle sera donc la direction du fil lorsque le sens de rotation changera ?
L'expérience montre qu'à l'instant du changement de sens, la bobine s'est immobilisée malgré la traction persistante pour une direction de fil dont le prolongement passe par la ligne de contact C avec le plan (schéma ci-dessous).
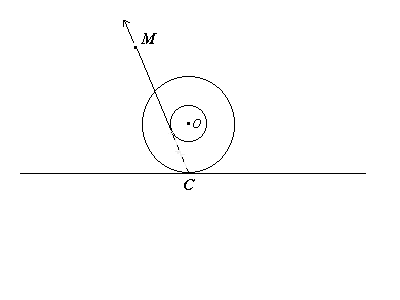
Ce point semble donc plus pertinent que O pour étudier la rotation de la bobine puisque selon que la ligne d'action de la traction passe à droite ou à gauche de C, le sens de rotation observé est horaire ou antihoraire.
Les clés de l'énigme
Bien entendu, comme nous y invite d'ailleurs l'observation qui précède, on peut calculer le moment des forces appliquées par rapport à C lorsque le fil a une direction quelconque (ce qui a l'avantage de n'avoir à prendre en compte que la seule force de traction du fil). Mais il ne faut pas compter sur ce calcul pour démystifier cette affaire et en explorer tous les aspects (on note par exemple que la nécessité d'un contact avec frottements n'apparaît pas). De la même façon, on pourrait résoudre par une construction géométrique le problème de statique relatif à la bobine en équilibre sur un plan incliné et soumise à trois forces qui sont donc nécessairement concourantes et de somme vectorielle nulle.
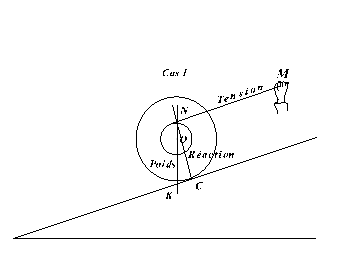 | 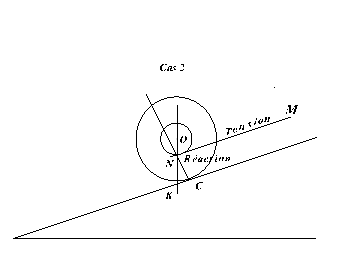 |
N est le point de concours des 3 forces. on notera qu'à une échelle donnée, le triangle NKC peut représenter la somme vectorielle P+T+R=0. On remarquera que l'inclinaison de la réaction du plan par rapport à la normale est plus forte en 2 (cas « paradoxal ») qu'en 1 (cas « normal »). Mais tout ceci est inopérant si on veut faire comprendre réellement le paradoxe apparent. Avant tout calcul de force ou de moment il serait bien préférable d'observer que si la bobine descendait en roulant sur le plan incliné, pour un tour effectué, elle aurait avancé de 2 π R alors que le fil ne se serait déroulé que de 2 π r. Comme ce fil n'est pas extensible, la bobine reste bloquée (à moins que, les frottements étant insuffisants, la bobine ne tourne tout en glissant sur le plan). Au passage on observe que si R=r, il n'y a plus de problème et la bobine descend sur le plan en roulant sans glisser.
Pour ce qui est du déplacement paradoxal sur plan horizontal (figure 4) on pourra remarquer :
a) qu'une tige posée verticalement sur un plan horizontal prend un mouvement de chute autour de A si on le soumet à une traction horizontale en un point quelconque plus haut ou plus bas que O (contact en A avec frottements) ;
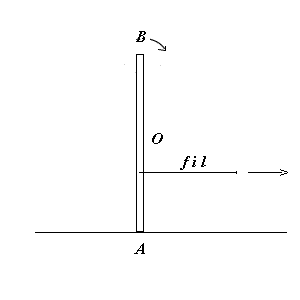
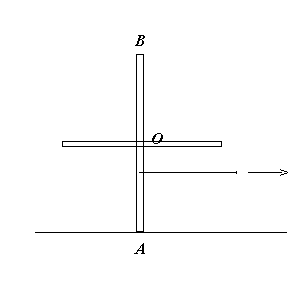
b) qu'il en serait de même pour cette croix... ;
c) ou pour cette « roue à rayons dont on aurait supprimé la jante ».
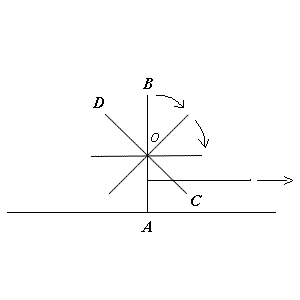
Mais ici la chute ne sera qu'amorcée car la tige CD ayant légèrement tourné elle aussi, elle viendra à son tour en contact avec le sol. On peut alors attacher le fil sur cette nouvelle tige verticale pour poursuivre le mouvement de rotation en sens horaire. On voit que, même si le fil est attaché en dessous de O, la roue basculera de diamètre en diamètre reproduisant ainsi les basculements infinitésimaux autour du point de contact réalisés dans l'expérience de la figure 4.
Au total, le sens commun voudrait que la bobine tourne toujours autour de son axe dans le sens de la force qui lui est appliquée. C'est oublier qu'il existe une force de contact avec le plan dont le moment par rapport à l'axe n'est pas nul (sans quoi la bobine se comporterait toujours suivant le « sens commun »). On comprend d'ailleurs que cette force ne passant pas par le centre n'est pas normale au plan et donc qu'il s'agit nécessairement d'un contact avec frottements. Le lecteur aura compris qu'une analyse qualitative de ce type est à mener avant tout calcul, appliquant en cela un principe fondamental de physique théorique résumé avec humour par Wheeler (et cité par J.-M. Levy-Leblond dans son ouvrage « La physique en questions » paru chez Vuibert) : ne jamais faire aucun calcul avant d'en connaître le résultat...
Pour citer cet article :
Observations et réflexions autour d'une bobine de fil, Georges Ferrachat, mai 2003. CultureSciences Physique - ISSN 2554-876X, https://culturesciencesphysique.ens-lyon.fr/ressource/Bobine.xml




