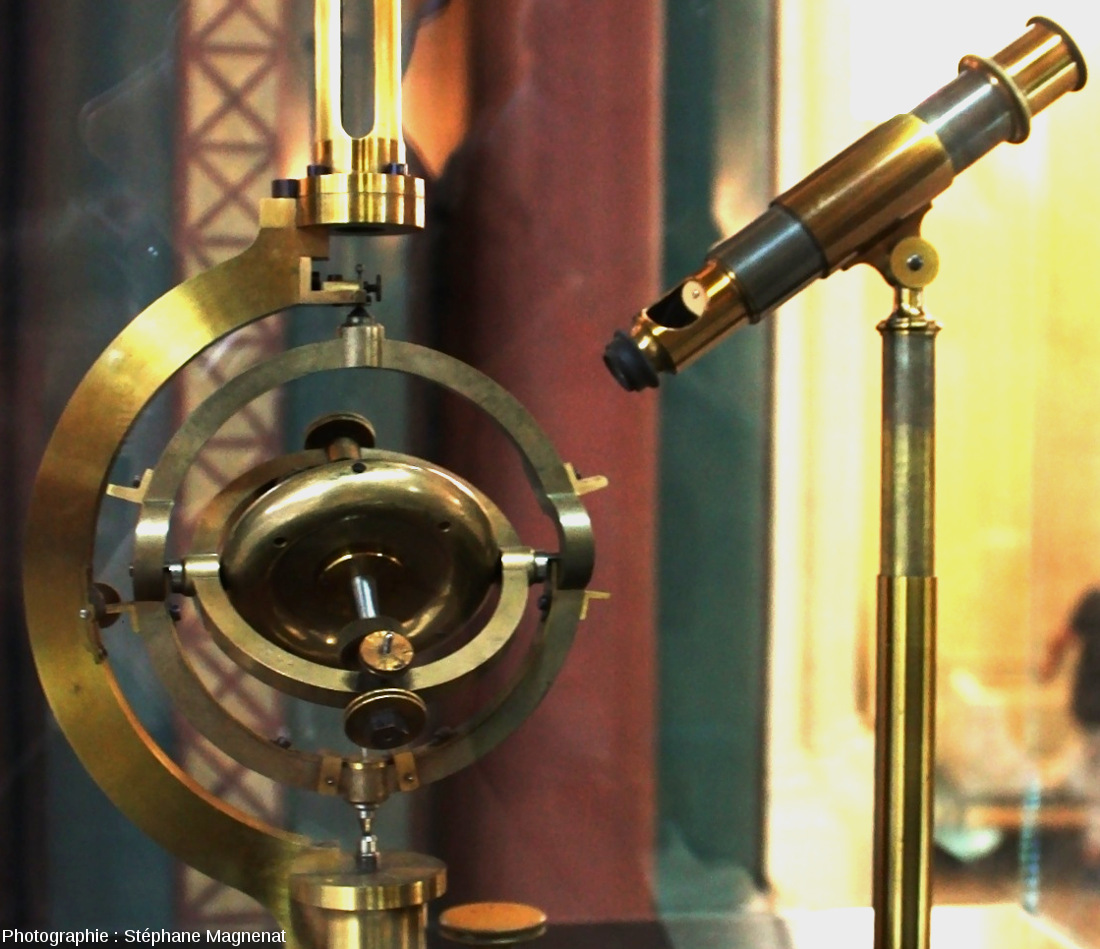Activer le mode zen
Ressource au format PDF
Mots-clés
- Terre
- rotation
- force de Coriolis
- pendule
- oscillation
Classification
La Terre tourne... Le gyroscope de Foucault
02/07/2018
Résumé
Les expériences qui ont fourni des preuves des mouvements de la Terre. Léon Foucault (1819-1868), son célèbre pendule et son gyroscope.
Table des matières
Transcription par Yves Gomas de la présentation d'Hugues Chabot du23 novembre 2015 à l'ENS de Lyon, donnée dans le cadre du cours pluridisciplinaire des écoles doctorales EPIC, PHAST et INFOMATH intitulé La Terre, sa forme, sa rotation, ses marées - Morceaux choisis mathématiques, géophysiques et historiques.
1. Quelles preuves des mouvements de la Terre ?
Les mouvements de la Terre ont été considérés pendant très longtemps comme très difficiles (voire impossibles) à détecter, en raison de la petitesse des effets attendus. Dans les Entretiens sur la pluralité des mondes habités (1686), Fontenelle fait dire à la Marquise : « Est-il possible qu'il ne laissera pas quelque petite marque sensible à laquelle on le reconnaisse ? »
En cette fin de XVIIe siècle, il n'y avait aucune preuve directe du mouvement de la Terre autour du Soleil : la parallaxe attendue était indétectable et l'aberration[1] était inconnue. Quant au mouvement de rotation sur elle-même, les variations de la pesanteur étaient connues mais controversées, l'aplatissement de la Terre n'était pas encore mesuré, et la déviation du mouvement de chute des corps non plus.
De la parallaxe planétaire à la parallaxe stellaire
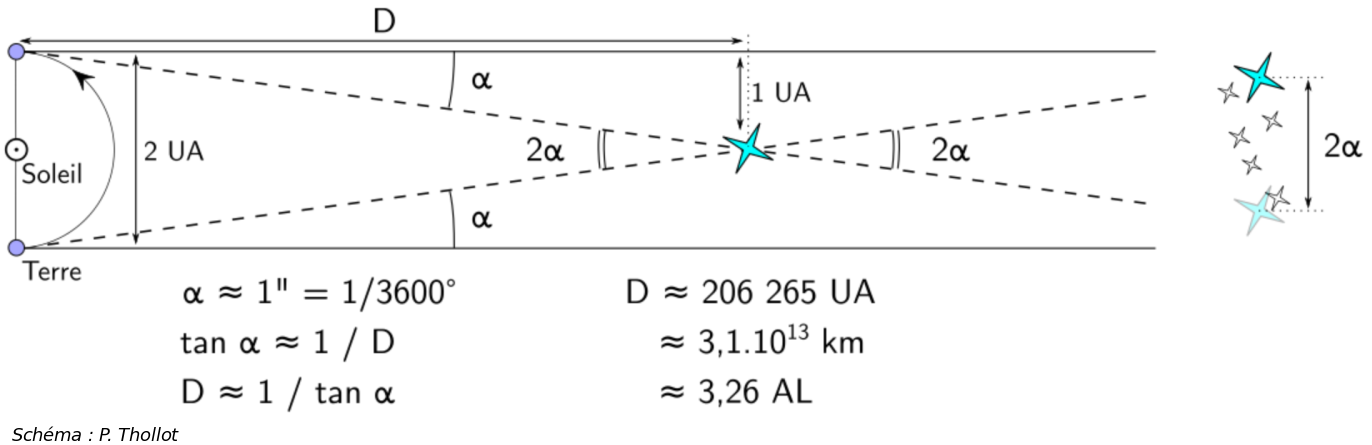
Le mouvement rétrograde apparent des planètes extérieures est dû à la parallaxe entre les planètes du système solaire. Seule la parallaxe planétaire est visible à l'œil nu (de quelques degrés pour Jupiter et Saturne à une bonne quinzaine de degrés pour Mars), mais le phénomène de parallaxe est généralisable à d'autres objets... On définit ainsi la parallaxe d'un objet céleste comme la moitié de celle qu'il montre du fait du mouvement de la Terre autour du Soleil en 6 mois (un diamètre de son orbite, soit 2 UA). Dit autrement, c'est, pour un observateur se décalant de 1 UA dans le système solaire, l'amplitude du mouvement apparent d'un objet céleste sur le fond du ciel. Dans l'analogie du pouce tendu devant soi, les deux yeux seraient écartés de 1 UA !
Sur la figure, à gauche, on a schématisé le Soleil et la Terre, avec sa révolution autour du Soleil au cours de 6 mois, pendant laquelle elle parcourt 2 UA. Au centre, on a représenté une étoile lointaine sans conserver l'échelle utilisée pour l'orbite de la Terre : elle est en réalité beaucoup plus loin. À droite, on a figuré le mouvement apparent de cette étoile par rapport à d'autres, situées beaucoup plus loin, et donc apparemment immobiles. L'étoile bleue, située à une distance D de la Terre, montre en 6 mois un mouvement apparent d'un angle de 2α. Pour α = 1", par définition, D = 1 parsec. Comme α est très petit (α ≈ π/180/3600 ≈ 5.10-6 radian) on peut faire l'approximation trigonométrique α ≈ sinα ≈ tanα ≈ 1/D, d'où on tire que la distance D ≈ 1/α ≈ 206265 UA, soit 3,26 AL (année-lumière).
Pour poursuivre au sujet de la parallaxe, on pourra consulter l'article « Les oppositions des planètes, observations autour des oppositions de Jupiter et Saturne en 2017 », sur Planet-Terre, dont cet encart est un extrait.
2. À la recherche de la parallaxe
L'absence de détection de la parallaxe des étoiles a été un obstacle important pour la propagation du système héliocentrique de Copernic. Les nouvelles idées n'apportaient pas de simplification par rapport à celles de Ptolémée, puisque Copernic travaillait comme lui avec des combinaisons compliquées de mouvements circulaires. Ceux qui ont été convaincus par le nouveau système ont apprécié l'introduction d'un ordre logique dans la liste des planètes, et par la possibilité d'établir des relations quantitatives entre le diamètre de leurs orbites et celui de la Terre. Les savants des XVIe et XVIIe siècles comprenaient bien les arguments mathématiques, mais ils ne disposaient d'aucun argument observationnel. Par exemple, la parallaxe des étoiles était indétectable pour Tycho Brahé, malgré la précision de ses mesures.
Il a fallu attendre 1838 pour que Bessel mesure la première parallaxe stellaire (61 Cygni : 0,3'' d'arc). Mais la découverte de l'aberration par Bradley en 1728 était déjà une preuve (inattendue) du déplacement de la Terre. L'interprétation "classique" de ce phénomène par la composition de la vitesse de la lumière et de la vitesse orbitale de la Terre donne pratiquement le même résultat que le calcul "relativiste"[2].
3. Les effets mécaniques de la rotation de la Terre sur elle-même
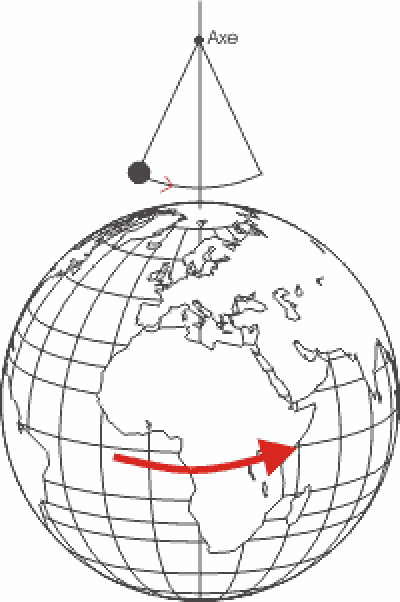
Un effet avait été pressenti par Newton, avec des arguments purement cinématiques. Un objet lâché depuis un point élevé n'a pas la même vitesse tangentielle qu'un point du sol, ce qui doit entrainer une déviation de la chute par rapport à la verticale.
Les mathématiciens ont longtemps renoncé à formaliser le problème, estimant que l'effet serait négligeable. Même Laplace dans son Exposition du système du monde (1796) admet que l'effet d'une force ne dépend pas de la direction dans laquelle elle s'exerce par rapport à la Terre. Laplace change cependant d'avis ensuite, et étudie mathématiquement la question lorsque des expériences sont effectuées[3]. L'expérimentation est très délicate, elle nécessite, pour être concluante, une chute sur une très grande hauteur, dans une atmosphère aussi stable que possible. Par exemple Ferdinand Reich (1799-1882) travaille en 1833 dans un puits de mine, il trouve une déviation de 28 mm pour une chute de 158 m.
Pour obtenir des résultats plus facilement observables, il faut imaginer des expériences plus longues qu'une simple chute, permettant de cumuler les effets de la rotation terrestre pendant plusieurs minutes.
4. Léon Foucault, expérimentateur
C'est par des expériences sur la vitesse de la lumière que Léon Foucault (1819-1868) fait d'abord connaitre son habileté expérimentale. Il conçoit et utilise des mécanismes et des systèmes optiques très précis. Il montre en 1850 que la lumière se propage plus vite dans l'air que dans l'eau, contrairement aux prévisions de la théorie "corpusculaire".
Source - © ... Bertall & Cie / Gallica
Nous n'avons pas d'éléments indiquant pourquoi il a engagé des recherches sur la rotation de la Terre. Mais il donne des indications sur le cheminement de ses idées. Il a constaté en 1851 qu'une tige d'acier fixée par une extrémité peut osciller dans un plan, et que ce plan ne tourne pas si le support est mis en rotation. La transposition de cette constatation le conduit à l'idée d'un pendule simple dont le support est fixé sur une table tournante. Le plan d'oscillation du pendule reste fixe par rapport à l'espace du laboratoire quand la table est en rotation.
Source - © 1902 in Notice scientifique sur le pendule du Panthéon, expérience reprise en 1902..., p.9 Figure 2. Stabilité du plan d'oscillation d'un pendule libre Le pendule libre est indépendant de son environnement. Si on tourne son support, le pendule oscille toujours dans le même plan (vu de l'extérieur). En prenant le support comme référentiel, le plan d'oscillation semble donc avoir tourné. | Source - © 2009 D'après Philippe Boeuf |
Pour avoir l'analogie exacte avec la Terre, il faudrait que l'expérience de la table tournante soit menée au pôle. Mais le phénomène subsiste dans le cas d'un horizon "oblique" par rapport à l'équateur, avec un ralentissement dans le mouvement apparent du plan d'oscillation.
Foucault commence par réaliser l'expérience du pendule dans sa cave, avec un fil de 2 m. Il la reproduit ensuite à l'Observatoire de Paris, avec une longueur de 11 m. Enfin, en mars 1851, il installe au Panthéon à Paris un pendule de 28 kg avec un fil de 67 m et une période de 16 s. Une pointe fixée à la boule du pendule ébrèche peu à peu un petit tas de sable placé sur une table, rendant visible la rotation du plan du pendule.
Cette expérience présentée en 1852 est vue par un public nombreux. Son caractère explicatif n'est pourtant pas évident : l'effet observable n'apparait pas immédiatement, les explications qualitatives sont loin d'être intuitives, et les calculs sont difficiles.
Source - © 1887 in La Nature, 2ème semestre, p.409, à voir par ex. sur Cnum
Figure 4. L'expérience du pendule de Foucault au Panthéon
Voir aussi Notice scientifique sur le pendule du Panthéon, expérience reprise en 1902.... Illustration très semblable parue le 5 avril 1851 dans le journal L'illustration.
Le mathématicien Louis Poinsot (1777-1859) suggère de remplacer le pendule par un solide en rotation, librement suspendu par son centre de gravité. Foucault imagine un dispositif expérimental qu'il nomme gyroscope, et en confie la fabrication à Froment. La difficulté est « de soustraire le corps qui tourne à la pesanteur, de le supporter par son centre de gravité sans agir autrement sur lui, sans lui imposer aucun lien qui le rattache à la terre ; il faut en faire plus qu'une planète, il faut en faire un petit astre isolé, perdu en quelque sorte dans les espaces et dégagé de toute action perturbatrice ».
L'appareil est formé d'une partie tournante (rotor) possédant une symétrie de révolution autour de son axe, et d'un système de suspension conçu pour laisser le rotor libre de tourner dans toutes les directions. Un montage auxiliaire, actionné à la main, donne au rotor une vitesse de 150 à 200 tours par seconde. L'axe de rotation reste fixe par rapport aux étoiles. La rotation de la Terre se traduit par le déplacement d'une longue aiguille liée au rotor devant une graduation fixée à la table. L'observation est possible également avec un petit microscope qui vise une graduation liée au support du rotor.
Source - © 2008 D'après Stépĥane Magnenat sur wikimedia, modifié Figure 5. Gyroscope de Foucault, modèle construit par Dumoulin Froment en 1852 Gyroscope exposé au Musée des arts et métiers. | Source - © ~1883 D'après Science Museum / Science & Society Picture Library Figure 6. Matériel pour l'expérience du gyroscope de Foucault, construit par Dumoulin-Froment vers 1883. Voir aussi le Recueil des travaux scientifiques de Léon Foucault... (1878) pour des planches explicatives des différents instruments et du montage |
Le public est convoqué pour voir l'expérience du pendule de Foucault, qui remporte un grand succès grâce à son caractère spectaculaire. Bien que la publicité ait été faite sur le thème « venez voir la Terre tourner », le résultat n'est pourtant pas sensible de façon immédiate et un spectateur pouvait dire : « je vois bien que le plan d'oscillation du pendule se déplace successivement vers la gauche, je vois bien la brèche faite dans le sable augmenter peu à peu, mais je ne saisis pas en quoi cela tient au mouvement de rotation de la Terre ».
La mécanique newtonienne s'applique à des mouvements absolus, et la nécessité de préciser les repères utilisés n'était pas toujours bien perçue dans ce cadre. Les expériences de Foucault exploitent l'inertie des mouvements dans des référentiels non galiléens, elles obligent les physiciens à être rigoureux !
Le pendule de Foucault est soumis à la force de pesanteur et à la force de Coriolis due à la rotation de la Terre sur elle-même. La période de rotation du pendule autour de son axe d'oscillation est T = TTerre/sin λ, où λ est la latitude du lieu où est fixé le pendule et TTerre la période de rotation de la Terre. La durée de rotation du pendule autour de son axe est ainsi de 24h aux pôles (λ = 90°) et est « infinie » à l'équateur (λ = 0°). À Paris, le pendule effectue une rotation complète en 31h47 min.
Quelques références sur le pendule de Foucault :
- Animation Flash du Pendule de Foucault [sciences.univ-nantes.fr]. Dans cette simulation, il est possible de modifier la latitude du pendule pour observer les oscillations.
- Expérience du pendule de Léon Foucault au Panthéon de Paris, en 1851 / De Fonvielle, W. - La Nature, n°756, 26 novembre1887. pp. 409-411 [Bibliothèque numérique du CNAM]
5. Pistes d'exploitation
6. Les autres articles du dossier La Terre, sa forme, sa taille, sa rotation :
- La Terre est ronde ! Ératosthène et la mesure du rayon terrestre
- Les mesures de méridien vont-elles confirmer la théorie de Newton ?
- La Terre ellipsoïde ? Les mesures de la gravité au XVIIIème siècle
- Clairaut et sa bande, l'expédition de Clairaut et Maupertuis en Laponie
- Les machines de lord Kelvin
- Les marées depuis Newton
Bibliographie
Stéphane Deligeorges, 1989. Foucault et ses pendules, Paris, Carré
Jacques Gapaillard, 1988. Le mouvement de la Terre, La détection de sa rotation par la chute des corps, Cahiers d'Histoire et Philosophie des Sciences, n°25
Jacques Gapaillard, 1993. Et pourtant elle tourne, Le mouvement de la Terre, Paris, Seuil, collection Science ouverte
Philippe Parais, Hugues Chabot, 1994. Le pendule et le gyroscope de Foucault dans les Comptes rendus de l'Académie des sciences (1851-1900), Sciences et Techniques en Perspective, 1, 27
William Tobin, 2002. Léon Foucault, Le miroir et le pendule, Paris, EDP Sciences
[1] Pour un observateur en mouvement, la direction apparente d'une source lumineuse dépend de la composante de sa vitesse perpendiculaire à la direction d'observation. Une analogie classique est qu'un observateur se déplaçant à l'horizontale dans une voiture sous une pluie verticale a l'impression que la pluie tombe vers lui en biais.
[2] Au zénith, le facteur multiplicatif pour la tangente de l'angle d'aberration est (1-v2 / c2)1/2. Ce facteur est très proche de 1, la vitesse orbitale de la Terre est v≈30 km.s-1, et on a v/c ≈ 10-4.
[3] Pierre-Simon de Laplace, 1803. Mémoire sur le mouvement d'un corps qui tombe d'une grande hauteur, Bulletin des sciences de la Société Philomathique de Paris, Prairial An 11 de la République (mai 1803). Cet article et, plus largement, l'historique de ce problème ont fait l'objet en 2014 d'une analyse par A. Persson. Elle est disponible sur le site Bibnum.
Pour citer cet article :
La Terre tourne... Le gyroscope de Foucault, juillet 2018. CultureSciences Physique - ISSN 2554-876X, https://culturesciencesphysique.ens-lyon.fr/ressource/Terre-tourne-Foucault.xml