Pourquoi n'y-a-t-il pas deux éclipses par mois ?

On va répondre à cette question que l'on s'était posée il y a quelques jours...

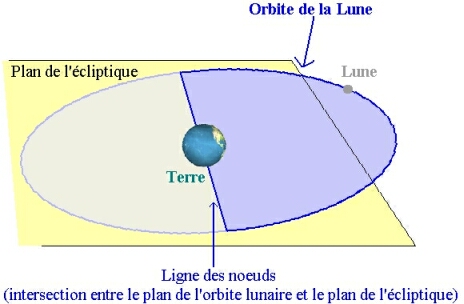
Il y aurait une éclipse (éventuellement annulaire) de Soleil toutes les nouvelles Lunes et une éclipse de Lune toutes les pleine lune si l'alignement Soleil-Terre-Lune était parfait à cette période du mois. Or, il n'en est rien, parce que le plan de l'orbite de la Lune est incliné d'un angle d'environ 5° par rapport au plan de l'écliptique (plus précisément, cet angle varie entre 5° et 5°18' en 173 jours). On appelle "ligne des noeuds" les deux points de l'orbite de la Lune en lesquels elle coupe le plan de l'écliptique.

Gabrielle Bonnet

L'orbite de la Lune est inclinée de 5° environ par rapport à celle de la Terre autour du Soleil, c'est-à-dire par rapport au plan de l'écliptique

Figure 1. Inclinaison de l'orbite de la Lune par rapport au plan de l'écliptique de la Terre

Pour que la Terre, le Soleil et la Lune soient alignés, il faut donc, en première approximation, que la ligne des noeuds soit confondue avec la droite Terre-Soleil. Or, la ligne des noeuds n'est pas fixe mais effectue un tour complet en 18,61 ans, et la ligne Terre-Soleil effectue un tour complet en 1 an.

Gabrielle Bonnet

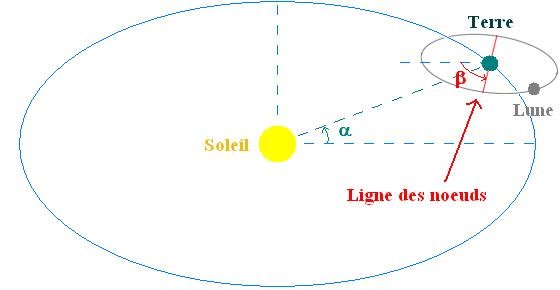
Figure 2. Configuration requise pour une éclipse

Si α est l'angle entre l'axe Terre-Soleil et une direction "fixe", on a

α = α₀ + 2 π/T_an t

où α₀ est une constante, t le temps, et T_an la période de rotation de l'axe Terre-Soleil, soit un an.

Si β est l'angle entre l'axe Terre-Soleil et une direction "fixe", on a

β = β₀ - 2 π/T_noeuds t

où β₀ est une constante, t le temps, et T_noeuds la période de rotation de l'axe Terre-Soleil, soit 18,6 ans.

On retrouvera donc des éclipses chaque fois que γ = β - α, angle entre la ligne des noeuds et l'axe Terre-Soleil, est égal à un multiple de π soit une "saison d'éclipses" qui se reproduit tous les 1/(1/T_noeuds + 1/T_an) soit tous les 173 jours (soit tous les 5 mois et demi environ)

On parle en effet de "saison d'éclipse" et non pas d'éclipse : il y a plusieurs éclipses par "saison d'éclipse"...

En fait, pour qu'il y ait alignement, il faut aussi, bien entendu, que la Lune passe par la ligne des noeuds à ce moment-là. On cherche la coïncidence de la ligne des noeuds avec l'axe Terre-Soleil ET avec l'axe Terre-Lune... Il faut donc ajouter à la condition ci-dessus que l'on doit être en période de pleine lune ou de nouvelle lune.

Cela est-il possible?

En fait, on notera qu'il n'y a pas besoin d'y avoir coïncidence "parfaite" pour avoir une éclipse : un décalage angulaire faible peut encore produire une éclipse visible. Comme la Lune tourne autour de la Terre en un mois et que la ligne des noeuds fait un tour en 18,61 ans, on comprend que la position de la ligne des noeuds change peu le temps d'arriver à la pleine ou à la nouvelle lune... et que l'éclipse puisse donc encore être visible.

A un endroit donné, on observera plus d'éclipses de Lune que d'éclipses de Soleil. Cela ne vient pas d'une plus grande fréquence, dans l'absolu, des éclipses de Lune, mais du fait que la zone de visibilité des éclipses de Lune est plus grande.

Gabrielle Bonnet

Les zones d'ombre et de pénombre projetées par la Lune sur la Terre ne couvrent pas toute la surface du globe. Cette zone correspond à la "zone de visibilité", à un instant donné, d'une éclipse de Soleil. Les éclipses de Soleil ont une "zone de visibilité" plus faible que celle des éclipses de Lune

Figure 3. Image d'une éclipse fictive dans l'océan Indien

Le Saros est un nom qui à l'origine désignait une période dans le calendrier Babylonien. Aujourd'hui, ce que l'on appelle Saros n'est plus exactement la même durée. Le Saros correspond à une période de 18 ans et 11 jours, soit 18,03 ans ou encore 38 saisons d'éclipse. Il s'agit du temps qu'il faut pour retrouver une "configuration d'éclipse" semblable.

Le rayon apparent du Soleil et celui de la Lune, vus de la Terre, sont quasiment identiques. Toutefois, les variations des distances Terre-Soleil (entre 1,47 × 10¹¹ et 1,52 × 10¹¹ m) et Terre-Lune (entre 3,6 et 4,1 × 10⁸ m) sont à l'origine de variations des rayons apparents de ces deux astres suffisantes pour avoir tantôt des éclipses annulaires, et tantôt des éclipses totales.

Voici quelques images de l'éclipse de 1999.

Cliquez ici pour agrandir l'image.

Figure 4. Le Soleil est encore visible

Figure 5. Le soleil n'est pas encore totalement occulté par la Lune

Figure 6. Situation d'éclipse totale