Activer le mode zen
Ressource au format PDF
Classification
La planète Mars en opposition et occultation par la Lune
20/12/2007
Résumé
La planète Mars est facilement observable fin décembre 2007 : opposition ; occultation par la Lune.
Table des matières
Pour les astronomes amateurs, décembre 2007 est une période privilégiée pour observer Mars et l'occasion pour tous d'aborder quelques notions simples d'astronomie.
La planète Mars sera bien visible en décembre 2007
En cette fin d'année 2007, la configuration Mars, Terre, Soleil présente plusieurs éléments remarquables : Mars est en opposition, relativement proche de la Terre, et assez haute sur l'horizon dans l'hémisphère Nord. Ces trois phénomènes, simultanés, facilitent l'observation de cette planète.
L'opposition de Mars
Les planètes du système solaire tournent autour du Soleil qui se trouve au foyer de leurs orbites elliptiques. On dit qu'il y a « opposition » lorsque qu'une planète, la Terre et le Soleil sont alignés, avec la Terre entre les deux : la planète et le Soleil sont à l'opposé pour un observateur terrestre (comme la Lune lors de la pleine Lune).
Source - © 2007 Dessin : Olivier Dequincey
Le Soleil et Mars sont en opposition par rapport à la Terre.
Le schéma ne respecte pas exactement les distances relatives et les excentricité des orbites. Le Soleil est à un foyer commun des orbites.
Dessin : Olivier Dequincey
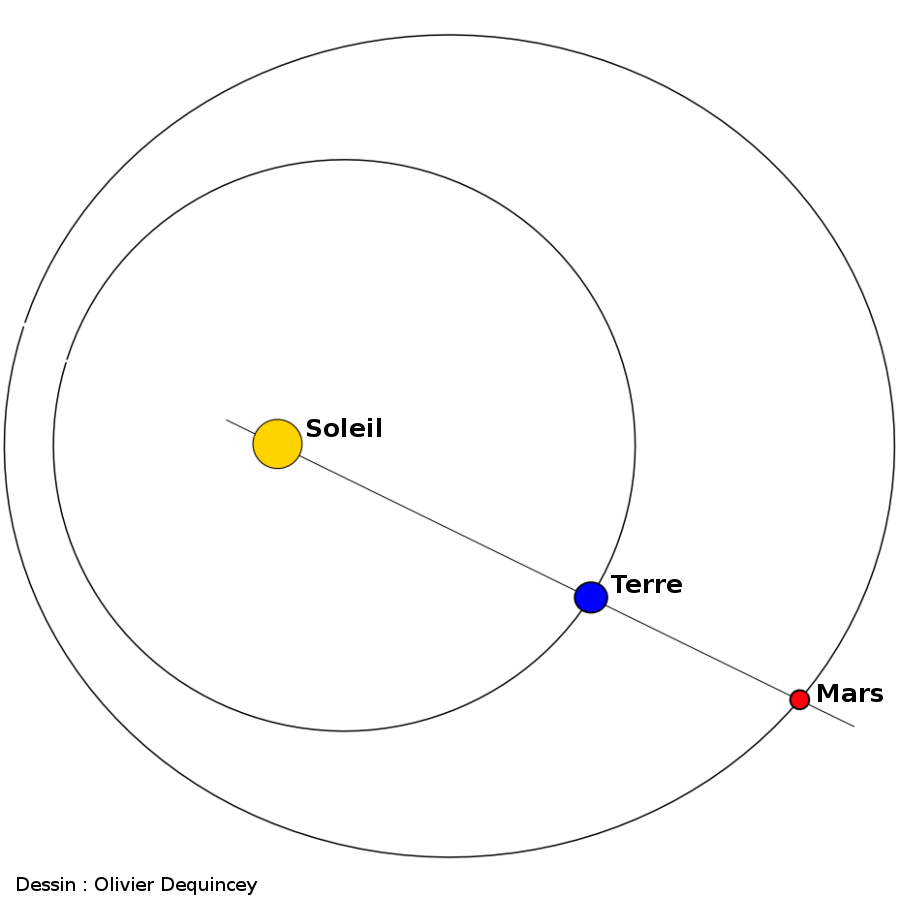
Figure 1. Mars en opposition
Le 24 décembre 2007, à 20h46 H.L.F. (Heure Légale Française), Mars et le Soleil sont en opposition. La nuit de Noël est une nuit de « pleine Mars » !
Périodicité des oppositions - Connaissant la période de rotation de la Terre (TT=365,25j) et celle de Mars (TM=687j, jours terrestres), il est possible de calculer la périodicité de ce phénomène.
Rétrogradation - Lors de la période encadrant une opposition, il y a rétrogradation de Mars. Le mouvement apparent de Mars dans le ciel est alors d'Ouest en Est, alors que le mouvement « habituel » est d'Est en Ouest, comme celui de la Lune.
Mars sera assez proche de la Terre
Dans le cas théorique d'orbites circulaires, chaque opposition correspond à la distance minimale Terre - planète. Du fait de la forte ellipticité de l'orbite de Mars (excentricité de 0,093 à comparer à l'orbite quasi-circulaire de la Terre d'excentricité 0,017), la distance Terre-Mars lors des oppositions varie entre 56 millions de km et 101 millions de km.
Les distances sont minimales lorsque la Terre et surtout Mars sont proches de leurs périhélies. La Terre sera au périhélie le 3 janvier 2008 et Mars était à son périhélie le 4 juin 2007. L'opposition de décembre 2007 n'est donc pas dans la situation la plus favorable. Le 18 décembre 2007, la distance Terre - Mars était minimale et valait environ 88 millions de km. Néanmoins, cette proximité relative facilite l'observation de Mars qui est brillante en cette fin d'année 2007. Même avec du matériel amateur, on observe la calotte polaire, la Valles Marineris, l'Olympus Mons .... Pour profiter d'une distance plus petite, il faudra attendre fin mai 2016 (76 millions de km) voire, mieux, fin juillet 2018 (58 millions de km).
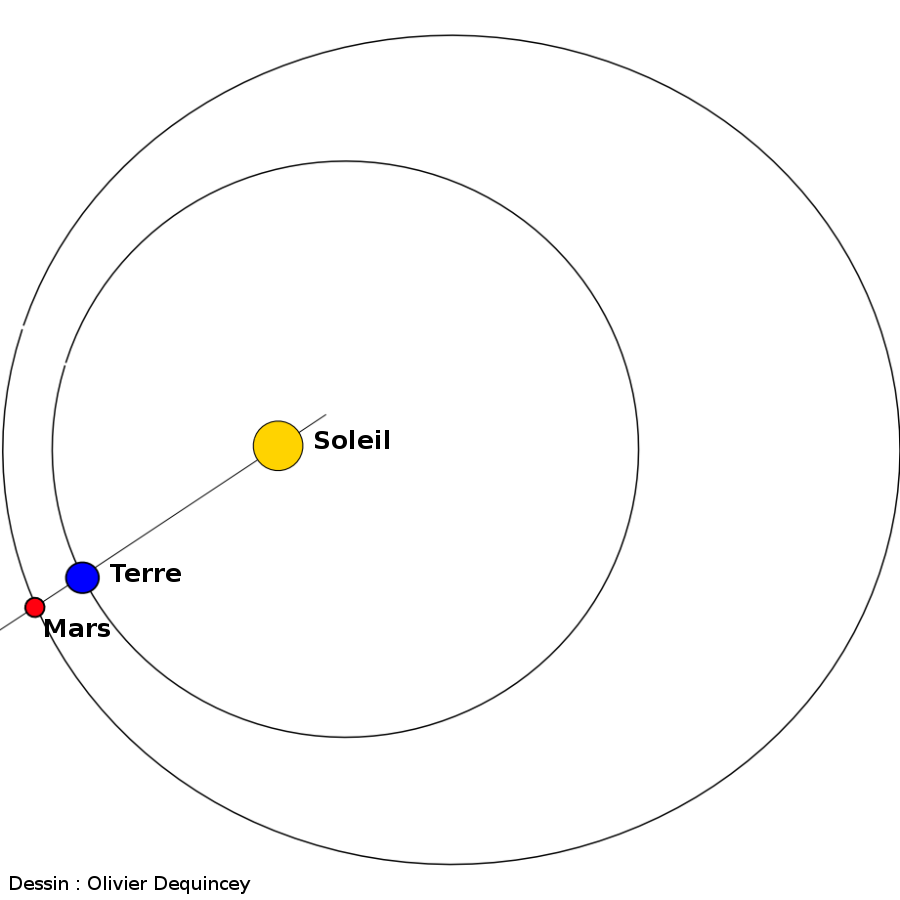
Source - © 2007 Dessin : Olivier Dequincey
Le Soleil et Mars sont en opposition par rapport à la Terre, et Mars est proche de son périhélie. La distance Terre-Mars est ici inférieure au cas de la figure 1 pour lequel Mars est plus proche de son aphélie.
Le schéma ne respecte pas exactement les distances relatives et les excentricité des orbites. Le Soleil est à un foyer commun des orbites.
Dessin : Olivier Dequincey
Excentricité, périhélie et aphélie - L'excentricité (e) d'une orbite elliptique est définie comme le rapport e=c/a, avec c la distance centre-foyer de l'orbite et a le demi grand axe de l'orbite. Les distances foyer - planète au périhélie (m) et à l'aphélie (M) s'expriment alors : m=a.(1-e) ; M=a.(1+e).
Mars apparaîtra haut sur l'horizon dans l'hémisphère Nord
Les pollutions lumineuses urbaines empêchent l'observation des constellations, astres et planètes proches de l'horizon. Le fait que Mars soit haut sur l'horizon en décembre facilite aussi son observation.
La hauteur sur l'horizon nocturne des planètes est dûe à l'inclinaison de l'axe de rotation de la Terre par rapport au plan de l'écliptique et à la position de la Terre sur son orbite. Dans l'hémisphère Nord, au solstice d'hiver, la hauteur sur l'horizon de l'écliptique est maximale la nuit. L'influence de la saison sur la hauteur de la Lune dans le ciel est expliquée dans un article publié conjointement sur CultureScience-Physique et Planet-Terre, ses conclusions sont généralisables aux planètes du système solaire
Occultation par la Lune
Le 24 décembre 2007 est aussi une nuit de pleine Lune (à 02h15 heure de Paris, nuit du 23 au 24). La Lune sera donc dans l'alignement Terre-Soleil à cette date (puisque la pleine Lune correspond à une opposition de Lune). Soleil, Terre, Lune et Mars seront donc presque parfaitement alignés. Si bien que le 24 décembre vers 05h H.L.F., soit quelques heures avant l'opposition de Mars, la Lune passera devant la planète rouge : on parle d'occultation.
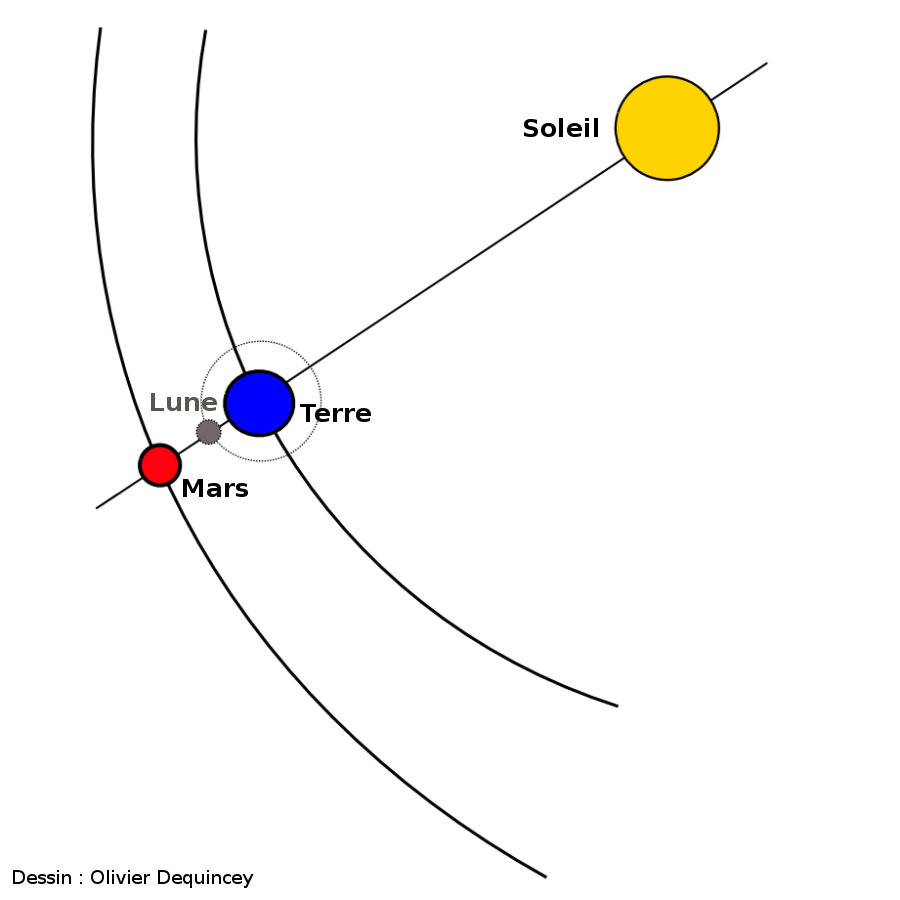
Source - © 2007 Dessin : Olivier Dequincey
Le Soleil et Mars sont en opposition par rapport à la Terre. La Lune, en position de pleine Lune (=opposition), occulte Mars.
Le schéma ne respecte pas exactement les distances relatives et les excentricité des orbites. Le Soleil est à un foyer commun des orbites.
Dessin : Olivier Dequincey
En France métropolitaine, Mars restera visible à proximité immédiate de la Lune : Mars sera à quelques minutes d'arc seulement du pôle Sud de la Lune et sera donc facilement localisable. Comme toute éclipse, l'observation de l'occultation dépend de la latitude de l'observateur : c'est en Scandinavie, ce 24 décembre au matin, que la Lune occultera totalement Mars.
Compléments d'informations
Périodicité des oppositions - Dans un repère héliocentrique, on choisit une opposition impliquant Mars comme origine des temps et comme direction de référence pour les angles. Soit θT et θM les angles respectifs des positions de la Terre et de Mars (0<θ<2π), et t le temps exprimé en jours. On peut écrire θ(t)=tx2π/T + k.2π ; k entier. Une opposition a lieu lorsque θT(t) = θM(t). Soit tx2π/TT + k.2π = tx2π/TM + k'.2π. Ce qui donne t= (k'-k).(TT . TM / TM - TT) = (k'-k) Topp. On obtient Topp= 779,9 jours, soit tous les 2 ans et 50 jours environ.
Quelques liens utiles :
- Ciel & Espace, décembre 2007 ;
- Quelques notions sur l'opposition de Mars, J Laskar (IMCCE) ;
- IMCCE : page proposant des outils de calcul des éphémérides ;
- L'orbite de la Terre sur le site de l'académie d'Aix-Marseille.
Pour citer cet article :
La planète Mars en opposition et occultation par la Lune, Olivier Dequincey, Catherine Simand, décembre 2007. CultureSciences Physique - ISSN 2554-876X, https://culturesciencesphysique.ens-lyon.fr/ressource/opposition-occultation-Mars-Lune.xml
