Activer le mode zen
Ressource au format PDF
Mots-clés
- fluide
- force de frottement
- nombre de Reynolds
- méthode d'Euler
- frottement fluide
Classification
Forces de frottement subies par un objet en mouvement dans un fluide
10/04/2003
Résumé
Le programme de Terminale S présente 3 expressions différentes pour la force de frottement subie par un objet en mouvement dans un fluide : cette force peut être proportionelle à la vitesse V de l'objet, à la vitesse au carré ou à V puissance 1,4. Cette variété d'expressions nous interpelle : d'où viennent-elles ? Ces trois expressions sont-elles les seules possibles ? Peut-on prédire quelle expression décrira adéquatement notre expérience ? Le programme, cependant, ne répond pas vraiment à ces questions : notre propos sera donc de clarifier la nature de ces 3 "régimes" différents et de donner les moyens de prédire la dépendance en V de la force de frottement fluide étudiée en Terminale S.
Table des matières
Introduction
Lorsqu'un objet est lâché dans un fluide (air, eau, etc...), il subit, outre son poids et la poussée d'Archimède, des forces de frottement fluide dont la dépendance dans les paramètres du problème (vitesse de l'objet, mais aussi nature du fluide ou forme de l'objet...) peut être complexe. La modélisation de ces forces de frottement fluide est essentielle pour la compréhension du mouvement de l'objet sur lequel elles s'exercent.
Le programme de Terminale S présente le problème ainsi : il y a trois différents "régimes" dépendant de la vitesse V de l'objet, dans lesquels les forces de frottement fluide ont les expressions suivantes :
- pour des vitesses V "faibles", les frottements fluides sont proportionnels à V
- pour des vitesses "plus élevées", ils sont proportionnels à V1,4
- enfin, pour des vitesses "très importantes", les frottements fluides sont proportionnels à V2
Notre propos sera de clarifier la nature de ces "régimes" et de donner les moyens de prédire la dépendance en V de la force de frottement fluide étudiée en Terminale S.
Les résultats expérimentaux
La force de frottement fluide exercée sur un objet en mouvement dépend du champ de vitesse existant au voisinage de cet objet. Or, si, à l'observateur naïf, le mouvement relatif du fluide (eau, air...) par rapport à l'objet peut paraître simple, en fait l'écoulement est souvent complexe et variable en fonction, entre autres, de la vitesse de l'objet. L'allure de l'écoulement a un impact crucial sur la valeur des frottements fluides.
L'écoulement dépend en fait, plutôt que du seul paramètre V, d'un nombre sans dimension, fonction à la fois de la vitesse V relative de l'objet par rapport au fluide, d'une taille caractéristique d de l'écoulement (par exemple, le diamètre de l'objet si celui-ci est une sphère), de la masse volumique ρ du fluide, et de sa viscosité η (en Pa.s). Ce nombre sans dimension est appelé nombre de Reynolds Re et vaut :
Re = V d ρ / η |
Voici quelques exemples d'écoulements fluides que l'on peut observer au voisinage d'une sphère en mouvement (NB : toutes les images d'écoulement qui suivent proviennent du site "aérotechniques"):
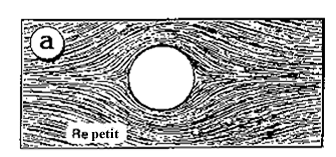
http://www.bls.fr/amatech/aerotechnique/trainees2/trai2vc1.htm
Cet écoulement est un écoulement laminaire. On l'observe pour des valeurs de Re < < 1
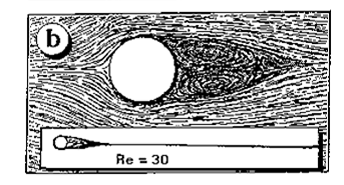
http://www.bls.fr/amatech/aerotechnique/trainees2/trai2vc1.htm
Pour un nombre de Reynolds plus élevé, on peut observer deux tourbillons en aval de l'objet

http://www.bls.fr/amatech/aerotechnique/trainees2/trai2vc1.htm
Re augmente encore, la sphère est suivie de tourbillons formant une "allée de Karman"
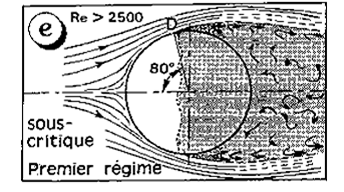
http://www.bls.fr/amatech/aerotechnique/trainees2/trai2vc1.htm
L'écoulement est fortement turbulent
Seul un domaine de valeurs de Re donne lieu à des calculs "exacts" :
Re ≪ 1. Plus précisément les calculs sont "exacts" au premier ordre du développement en Re. Dans ce domaine, on montre qu'on peut affirmer que F est proportionnelle à V avec une bonne approximation, ce qui est corroboré par les résultats expérimentaux.
La résolution théorique du problème est beaucoup plus ardue à Re > 1, ce qui fait que les résultats que l'on donne dans ce domaine-là sont essentiellement des constatations expérimentales. Ainsi, on constate que pour une sphère et Re compris entre 30 et 800 environ, F est proportionnelle à V1,4 avec une assez bonne approximation (les limites du domaine dans lequel F est proportionnel à V1,4 dépendent évidemment de la précision recherchée!). Pour 103 < Re < 105 ou 106, F est proportionnelle à V2, et pour Re > 106 ou 107, F est là encore proportionnelle à V2, mais le coefficient de proportionnalité est différent.
Pour prédire avec une assez bonne approximation la dépendance en V des forces de frottement fluide s'exerçant sur un objet en mouvement, il suffit donc de connaître la valeur du nombre de Reynolds (tant que celui-ci ne se situe pas dans une zone de transition entre deux régimes différents) correspondant à l'écoulement.
Les bases théoriques
Explication intuitive de la signification du nombre de Reynolds
Quel est le critère intuitif utilisé dans la vie courante pour déterminer si un fluide est "visqueux" ou si un fluide est au contraire "très fluide"?

On jette de l'eau et du miel sur une table... lequel va le plus loin?
Supposons que l'on jette de l'eau et du miel sur une table. L'eau va s'étaler tandis que le miel va peu "couler". Quel est le nombre qui caractérise ce comportement? Est-ce la viscosité η? Est-ce un autre nombre? Nous allons essayer de le déterminer en analysant cette expérience.
Si une portion de fluide de "rayon" caractéristique D lancé initialement à la vitesse V se déplace sur une longueur L avant de s'arrêter, la variation d'énergie cinétique de ce fluide est de l'ordre de m V2 (comme ceci est un calcul d'ordre de grandeur on oublie les facteurs 1/2) soit ρ D3 V2.
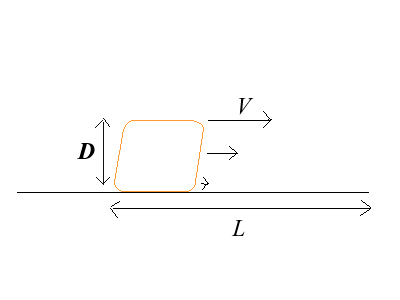
Le miel (très schématisé!) à l'instant initial : c'est une portion de fluide de taille D, dans lequel le gradient des vitesses est de l'ordre de V/D : on a lancé le fluide à la vitesse V, mais si la partie libre du fluide peut continuer sur sa lancée à la vitesse V, la partie en contact avec la table a, du fait des contraintes visqueuses, une vitesse nulle.
Estimons à présent le travail des forces de frottement fluide.
Par définition de la viscosité η du fluide, les contraintes visqueuses sont de l'ordre de : η S grad v, η étant la viscosité du fluide, S la surface sur laquelle s'exercent ces contraintes et grad v les gradients de vitesse dans le fluide. Le travail des frottements fluides sur une distance L est donc de l'ordre de η S grad v L (on donnera plus tard une définition plus précise de la force de frottement fluide mais cet ordre de grandeur suffit pour l'estimation que l'on souhaite faire ici).
Or, S est de l'ordre de D2, et grad v est de l'ordre de V/D (c'est le rapport de la variation de la vitesse à l'intérieur du fluide entre la table - au niveau de laquelle la vitesse est 0 - et la partie supérieure de la portion de fluide - lancée à la vitesse V - sur la taille D caractéristique de l'écoulement). Par suite, le travail des forces de frottement fluides est de l'ordre de η D2 V/D L.
La variation d'énergie cinétique du fluide entre son lancement et le moment où il s'arrête (après avoir parcouru la distance L) est égale au travail des forces de frottement fluide sur ce parcours, par conséquent, ρ D3 V2 = η D2 V/D L donc L/D = V D ρ / η = Re. Le rapport L/D est donc égal au nombre de Reynolds Re.
Si L/D est grand devant 1 (donc si Re > 1), le fluide va couler longtemps avant de s'arrêter, il sera donc "très fluide", si L/D est au contraire plus petit que 1 (c'est-à-dire lorsque Re ≪ 1), le fluide va très peu couler avant de s'arrêter : c'est un fluide fortement visqueux. On voit donc que la notion "intuitive" de viscosité ne correspond pas simplement à la valeur de η, mais au nombre de Reynolds. Pour un même fluide, selon la vitesse et la dimension des écoulements mis en jeu, le fluide se comportera comme un fluide "très visqueux" ou au contraire comme un fluide "très fluide". Les différents régimes que l'on observe expérimentalement confirment cette idée intuitive : la nature de l'écoulement dépend bien du nombre de Reynolds et non de la vitesse V seule.
L'équation de Navier-Stokes
L'équation de Navier-Stokes est le cadre théorique permettant de décrire le champ de vitesse dans la plupart des fluides étudiés en Terminale S.
Elle dépend de deux hypothèses :
- la première est qu'on a affaire à un fluide "Newtonien", c'est-à-dire que les contraintes de viscosité dépendent linéairement des valeurs instantanées des vitesses de déformation (les vitesses de déformation instantanées sont elles-mêmes directement reliées au gradient de vitesses)
- la deuxième est que l'on peut négliger les effets de compressibilité du fluide (pour un avion supersonique, cette hypothèse n'est pas vérifiée)
Dans ces conditions, on a, si on note ρ la masse volumique du fluide, v la vitesse relative du fluide par rapport à l'objet, ρ f les forces volumiques appliquées au fluide (par exemple, le poids par unité de volume ρ g), et p la pression du fluide :
ρ ∂v/∂t + ρ (v.grad)v = ρ f - grad p + η Δv |
On rappelle que le gradient (grad) est une dérivée première par rapport aux coordonnées d'espace alors que le Laplacien (Δ) est une dérivée seconde
Expression de la force de frottement fluide
La force de frottement fluide F fait intervenir deux composantes : une composante proportionnelle aux gradients de vitesse existant au voisinage de la paroi, et une autre qui dépend de la pression p dans le fluide. Si on note p0 la pression statique solution de l'équation ρ f - grad p0 = 0, et p' la différence p' = p - p0, on a
F = ∫∫surface ( [σ].n + p' n) dS |
où n est le vecteur normal à la surface de l'objet et [σ] est une matrice dont les éléments sont de la forme : η × des combinaisons linéaires des différentes composantes du gradient de v. L'expression de F dépend donc de la nature de l'écoulement au voisinage de la paroi de l'objet et, par suite, de la valeur du nombre de Reynolds.
Nombre de Reynolds, simplifications de l'équation de Navier-Stokes, et différents régimes
Si on compare les termes ρ (v.grad)v et η Δv de l'équation de Navier-Stokes, on voit que, si on se place à un échelle de distance caractéristique de l'écoulement d, le premier est de l'ordre de ρ V2/d, alors que le second est de l'ordre de η V/d2 (on se contente ici de remplacer les dérivées partielles spatiales par des divisions par d). Si on calcule le rapport entre ces deux nombres, on trouve qu'il est de l'ordre de V d ρ / η : ce rapport est égal au nombre de Reynolds.
Le nombre de Reynolds caractérise donc le rapport entre les effets cinétiques (qui correspondent au premier terme) et les effets de viscosité (qui correspondent au deuxième terme) à l'intérieur du fluide. Lorsque le nombre de Reynolds est petit, les effets de viscosité dominent tandis que lorsqu'il est grand, ce sont les effets cinétique qui dominent : ceci corrobore les résultats trouvés en 1.
Nombre de Reynolds très petit devant 1

http://www.bls.fr/amatech/aerotechnique/trainees2/trai2vc1.htm
Lorsque le nombre de Reynolds est très petit devant 1 (régime laminaire), les effets cinétiques (correspondant au terme non-linéaire ρ (v.grad)v de l'équation de Navier-Stokes) sont négligeables devant les effets de viscosité. On se retrouve donc avec une équation différentielle linéaire en v et p : ρ ∂v/∂t = ρ f - grad p + η Δv qui devient ρ f - grad p + η Δv = 0 dans le cas d'un régime permanent (ρ ∂v/∂t = 0).
On a défini p0, la pression statique, comme la solution de l'équation ρ f - grad p0 = 0, et p' comme la différence p' = p - p0 (cf 3.) : on obtient alors l'équation :
grad p' = ρ Δv |
Conséquences de la linéarité de l'équation de Navier-Stokes dans le cas Re ≪ 1 :
la vitesse de l'objet en mouvement dans le fluide intervient dans la résolution de cette équation par la donnée des conditions aux limites au voisinage de l'objet (si la paroi de l'objet se déplace à la vitesse V, le fluide au contact de la paroi est aussi animé d'une vitesse V). Comme l'équation différentielle est linéaire, les solutions v(r) et p'(r) de l'équation différentielle dépendent linéairement de la condition aux limites V. Par suite, la force de frottement fluide F dépendant linéairement de v(r) et de p'(r), F dépend elle aussi linéairement de V.
Dans le cas particulier d'une sphère rigide, on calcule de façon exacte la force de frottement fluide, et l'on obtient l'expression suivante pour F :
F = -3 π η D V où D est le diamètre de la sphère
Nombre de Reynolds supérieur à 1000

http://www.bls.fr/amatech/aerotechnique/trainees2/trai2vc1.htm
Lorsque le nombre de Reynolds n'est plus petit devant 1, l'écoulement change : on ne peut plus considérer les effets cinétiques comme négligeables, et si Re est très grand, l'écoulement devient fortement turbulent. Dans ce domaine de nombre de Reynolds, l'équation de Navier-Stokes ne peut pas être simplifiée pour donner une équation linéaire, par contre, on peut être tenté de supprimer le terme de viscosité pour ne garder que le terme cinétique. On voit alors que l'équation fait intervenir (v.grad) v, c'est-à-dire un terme de degré 2 en V. Ceci peut nous faire supposer que p'(r), et, par suite la force F, sera proportionnelle à V2. Effectivement, pour des nombres de Reynolds supérieurs à 1000, on constate que la force de frottement fluide est proportionnelle à V2.
Nombre de Reynolds compris entre 30 et 800
Ce domaine est intermédiaire entre les domaines étudiés précédemment. On peut supposer que, dans ce "domaine de transition", on va avoir un régime intermédiaire entre le cas où F est proportionnelle à V et celui où F est proportionnelle à V2. La situation étudiée est complexe, cependant, nous allons essayer de donner une idée très simplifiée, approximative, de l'origine de la dépendance de la force F en V dans cas là.
Tant que 30 < Re < 800 (les limites données à ce domaine ne sont pas des valeurs "exactes"!), on peut séparer l'espace en deux zones :
- presque partout, les effets cinétiques dominent devant les effets de viscosité
- très près de l'objet, cependant, les effets de viscosité dominent. La zone où les effets de viscosité dominent est appelée "couche limite".
On peut estimer son épaisseur : par définition, la frontière de la couche limite correspond à la surface sur laquelle les effets cinétiques et les effets de viscosité sont du même ordre : ceci signifie que ρ (v.grad)v est de l'ordre de η Δv. Si on appelle δ l'épaisseur de la couche limite autour d'une sphère de diamètre D, on a donc ρ V2/D = η V/δ2, soit δ = (ν D/U)1/2 (voir note).
On peut estimer alors la valeur de la force de frottement fluide F :
F est proportionnel à η V S/δ donc est de l'ordre de η0,5 R2 π-0,5 V1,5
En fait, le problème est plus complexe, et cette estimation de la dépendance en V de la force F ne fait que donner "un ordre d'idée" de la dépendance réelle. La force réelle, trop complexe pour se résumer à une simple puissance de V, peut cependant, d'après les résultats expérimentaux, être bien approchée par une une constante de proportionnalité que multiplie V1,4.
La transition entre le régime de dépendance en V1,4 et le régime de dépendance en V2 se fait lorsqu'il se produit un décollement de la couche limite et qu'un importante zone de turbulence fait son apparition.
pour estimer l'ordre de grandeur du terme en ρ (v.grad) v, nous avons utilisé la distance caractéristique D, c'est-à-dire la taille de l'objet, tandis que pour le laplacien nous avons utilisé l'épaisseur de la couche limite. Ceci se justifie parce que, dans l'expression (v.grad) v, le gradient est calculé suivant la direction de v, c'est-à-dire tangentiellement à la surface de l'objet : dans cette direction, la longueur caractéristique est la taille de l'objet, c'est-à-dire D. La Laplacien, par contre, est une somme de dérivées secondes d'espace, qui fait intervenir a priori toutes les directions d'espace : δ étant petit devant D (la zone dans laquelle les effets de viscosité dominent est très petite) le terme dominant dans le Laplacien Δ v est en V/δ2 et non V/D2.
Pour citer cet article :
Forces de frottement sur un objet en mouvement dans un fluide, Gabrielle Bonnet, Bernard Castaing, Hervé Gayvallet, avril 2003. CultureSciences Physique - ISSN 2554-876X, https://culturesciencesphysique.ens-lyon.fr/ressource/MecaFlu.xml




