Activer le mode zen
Ressource au format PDF
Mots-clés
Classification
Le GPS - Principe de localisation dans l'espace (1/2)
14/10/2019
Résumé
Article tiré de la conférence sur le GPS donnée par Jean-Pierre Lièvre à l'ENS de Lyon.
Table des matières
Introduction
Cet article est découpé en deux volets :
- Le principe de localisation dans l'espace est développé dans cet article.
- la physique du GPS est présentée dans l'article suivant : Le GPS - La physique du GPS (2/2)
1. Principe général de la localisation d'un point dans l'espace
Dans cette première partie nous allons aborder la localisation d'un point dans l'espace.
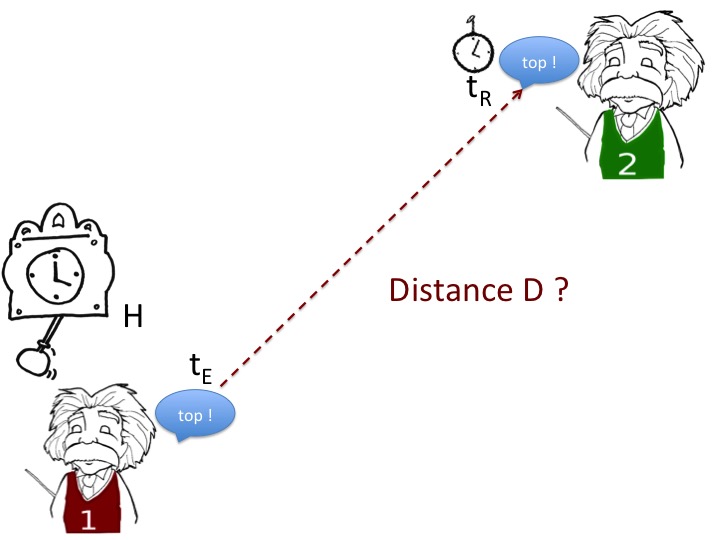
Sur la figure 1, on souhaite localiser le presonnage numéro 2 et trouver sa distance D par rapport à l'horloge H.
La personne 1 qui est sous l'horloge H envoie des « top » toutes les minutes. Le signal est émis au temps tE et l'onde se propage pour arriver sur le personnage 2.
Figure 1. Localisation dans un plan |
Le personnage 2 va recevoir le « top » au temps tR.
Comme il connait tE, il est capable de savoir à quelle distance D il est situé de l'horloge :
il mesure sur son propore chronomètre tR, il connait la vitesse du son dans l'air et peut ainsi remonter à la distance D qui le sépare de l'horloge.
D = c (tR - tE) = c ΔT
Le principe fondamental du GPS repose sur cet exemple : c'est un calcul de distance à l'aide de la mesure d'un signal dont on connait les dates d'émission et de réception et la vitesse de propagation.
2. Localisation d'un point dans un plan - 2D
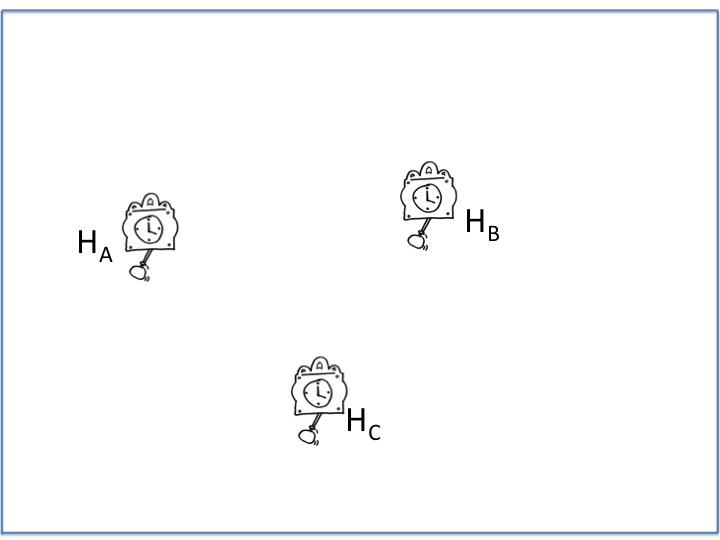
On dispose maintenant plusieurs horloges pour localiser une personne dans un plan, figure 2.
Dans cet exemple, trois horloges différentes HA, HB, HC émettent des sons différents afin de pouvoir les identifier au niveau de la réception. On pourra donc savoir à quelles distances le personnage se trouve des différentes horloges.
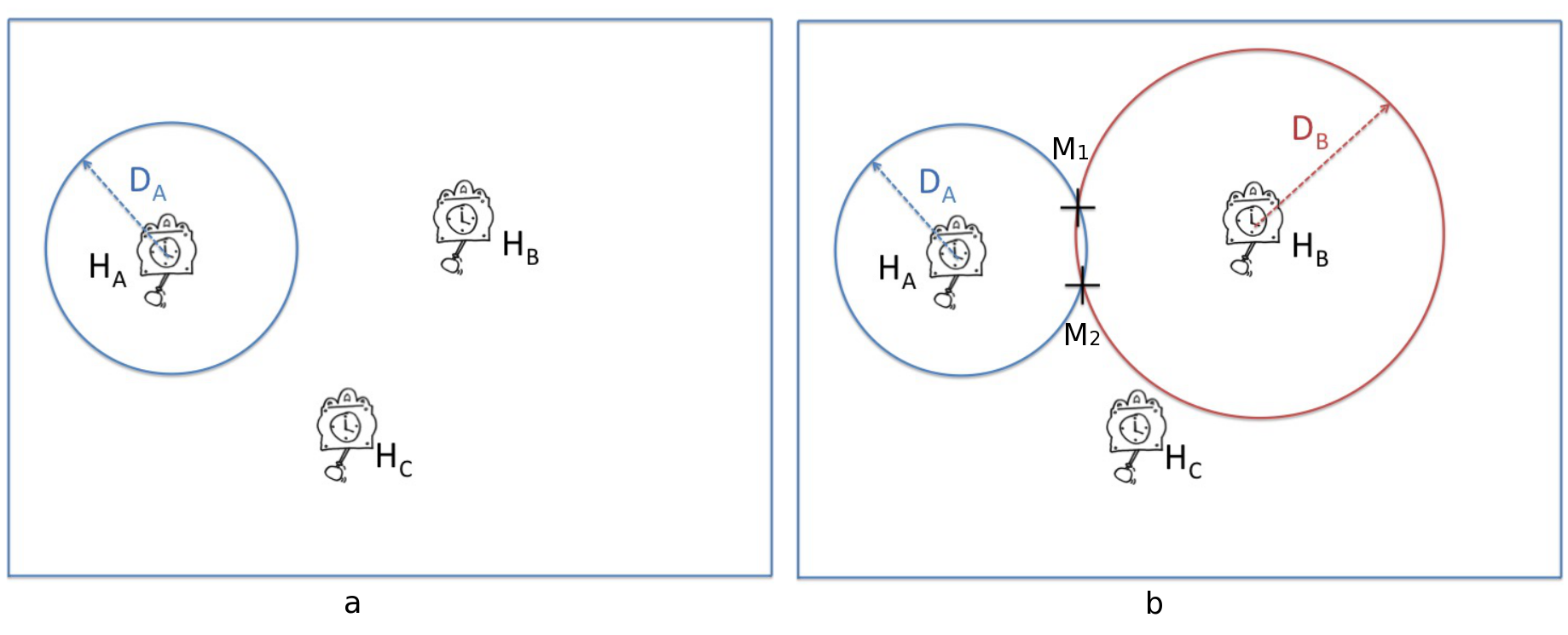
À l'aide de l'exemple précédent, on détermine la distance DA qui sépare le presonnage de l'horologe HA, figure 3 a). De la même manière le personnage se trouve aussi sur le cercle de rayon DB, figure 3 b).
Il existe deux points d'intersections. Le personnage est placé soit en M1 soit en M2.
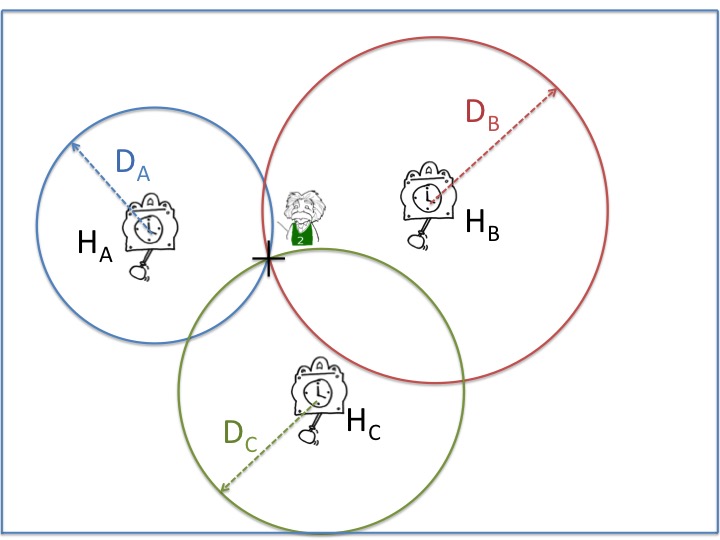
À l'aide de la troisième horloge on sait que le presonnage est aussi sur un cerle centré sur HC et de rayon DC. Cela permet de conclure que le personnage est localisé au point M2, figure 4.
Nous venons de voir le principe de localisation d'un point dans un plan. C'est très simple.
Sur le sujet de la localisation d'un point dans l'espace, on pourra consulter l'article : Repérage par le son des batteries ennemies Verdun 1916-1917 - Ou comment pouvait-on repérer les canons allemands lors de la Grande Guerre ?
On notera que dans cet exemple, les points HA, HB, HC sont des points fixes. Par ailleurs il est nécessaire de connaître très précisément la vitesse de propagation des ondes, pour remonter au calcul des distances.
De plus, ici nous n'avons pas pris en compte les incertitudes de mesure qui se répercutent sur localisation d'une zone plutôt que d'un point.
3. Localisation dans l'espace - 3D
3.1 Réseau de satellites
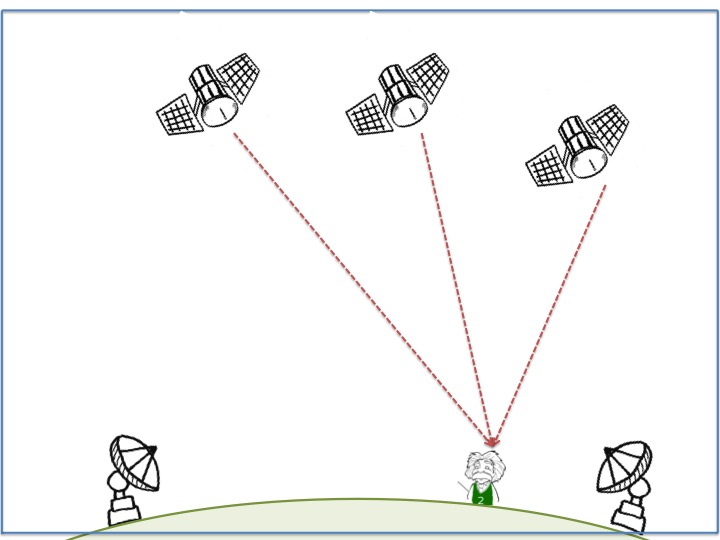
L'utilisateur est, cette fois, dans un espace à 3 dimensions et souhaite se repérer. Il utilise un ensemble de satellites munis d'horloges atomiques synchronisées les unes avec les autres, figure 5.
Maintenant, les points repères ne sont plus des points fixes. Il est alors nécessaire de connaître les positions exactes des satellites en chaque instant. Cette opération va être réalisée par des stations de contrôle régulièrement disposées sur Terre pour communiquer avec les satellites.
Chaque satellite transmet par ondes électromagnétiques son identification, afin de pouvoir déterminer de quel satellite provient chaque signal. Il envoie aussi des informations pour que l'on puisse connaître sa position et une convention de date d'émission de son signal.
À partir de l'intervalle de temps entre l'émission tE et la réception tR, il est possible de calculer les temps de parcours, les distances aux différents satellites et finalement de trouver sa position sur Terre.
3.2 Principe de localisation
Le principe de la localisation tridimensionnelle n'est pas beaucoup plus compliqué que pour la localisation bidimensionnelle.
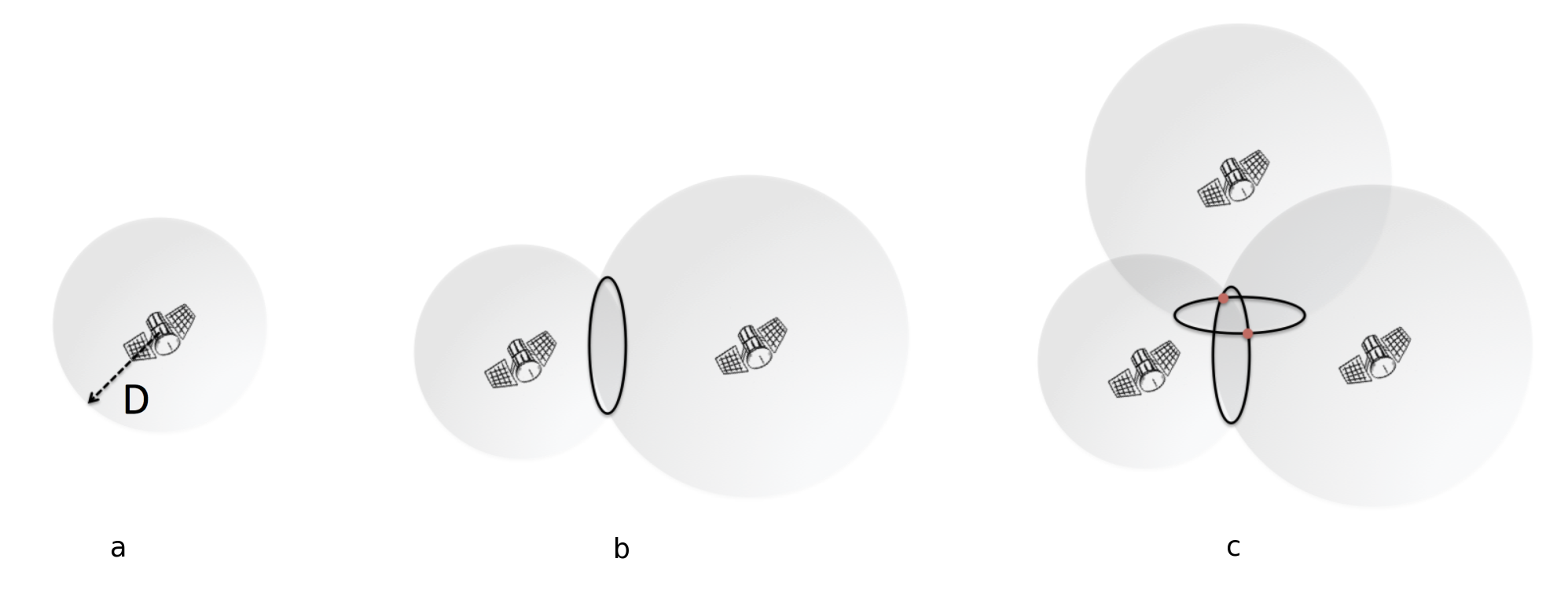
Avec un satellite on accède à la distance D. Le personnage est situé sur une sphère de rayon D centrée sur le satellite, figure 6 a.
Lorsqu'on dispose de deux satellites, les solutions de position sont sur le cercle d'intersection des deux sphères centrées sur les deux satellites, figure 6 b.
Avec maintenant trois satellites, il reste 2 points d'intersection, figure 6 c. Pour lever l'indétermination, on aura besoin de quatre satellites.
3.3 Mesure de temps et précision
- Mesure de temps
Le problème de localisation dans l'espace repose sur la mesure d'un temps de propagation. La date d'émission est mesurée sur les horloges atomiques présentes dans les satellites. Elle est donc déterminée très précisément. Par contre les horloges des récepteurs GPS des utilisateurs (horloges à quartz) n'atteignent pas une telle précision.
L'horloge du récepteur introduit une erreur systématique sur la mesure de la date de réception. Autrement dit, le temps à la réception est entaché d'une erreur ΔT.
On mesure ainsi une pseudo distance D' :
D' = c (tR - tE + ΔT) = D + ΔD
Il faut donc compenser, au niveau du récepteur, cette erreur par un même ΔD, pour arriver en un point unique.
L'utilisation d'un quatrième satellite permet de gagner en précision, d'ajuster l'écart de distance pour déterminer la position de l'utilisateur ainsi que la date.
Mais ce n'est pas tout. Une précision colossale est nécessaire pour déterminer les distances.
- Précision
En effet, la vitesse de propagation d'une onde életromagnétique dans le vide est très grande : c = 299 792,458 km/s. Les ondes parcourent 1 mètre en 3 nanosecondes (3 milliardièmes de secondes !).
Une erreur d'un millionième de seconde entraîne une erreur de plus de 300 m sur la position.
Or les exigeances initiales des systèmes de positionnement sont d'avoir une précision sur la position de quelques mètres. Cela impose alors d'être précis à quelques dizaines de nanosecondes !
Nous allons voir dans l'article suivant comment s'approcher de cette précision et découvrir toute la physique impliquée dans le système de positionnement.
Article suivant :
Pour citer cet article :
Le GPS - Principe de localisation dans l'espace (1/2), octobre 2019. CultureSciences Physique - ISSN 2554-876X, https://culturesciencesphysique.ens-lyon.fr/ressource/GPS-1.xml