Aire d'un film de savon et loi de la réfraction - quel rapport ?

Nous avons fabriqué une cellule en plexiglas formée de deux espaces dont l'épaisseur est différente, figures 1 et 2.

Figure 1.  Cellule transparente en plexiglas composée de deux lames d'air d'épaisseur différente a) Cellule posée à plat sur la table, b) Vue de trois-quart de la cellule et annotation des épaisseurs e1 et e2

Figure 2.  Mise en évidence du film de savon dans les deux espaces d'épaisseur différente

La cellule mesure environ 20 cm de côté. Dans l'espace le plus fin, l'épaisseur e₁ est telle que : e₁ = 7,7 mm, et dans la région la plus large : e₂ = 16,7 mm.

Nous réalisons un film de savon, figures 2 et 3, qui s'étend du plot A et parcourt une partie de son chemin dans la partie fine de la cellule et l'autre partie de son chemin dans la partie large de la cellule pour venir s'accrocher au plot mobile B. Dans cette étude, on considère que le film de savon est en deux dimensions, on néglige ainsi l'effet de la gravité. Aux temps courts les efforts de capillarité sont bien supérieurs à la gravité.

Figure 3.  Le film savonneux se place entre le plot A et le plot B. Le plot B est mobile sur toute la longueur de la cellule

Pour former le film de savon, il est nécessaire en amont de mouiller toutes les parois. Nous venons ensuite faire couler le liquide savonneux dans la tranche de la cellule. Cette opération demande du soin pour éviter que de nombreuses petites bulles viennent se superposer au film et le perturber. Plusieurs films se créent lors de cette opération, s'accrochant aux différents plots. Il faut alors délicatement casser les films qui ne nous intéressent pas pour garder celui existant entre le plot A et le plot mobile B.

Sur les figures 4 et 5, nous observons le film de savon ainsi créé. L'ajout d'un fond noir nous permet de le mettre plus en évidence.

Figure 4.  Photo du film de savon de part et d'autre de la marche à l'intérieur de la cellule

Figure 5.  Photo du film de savon de part et d'autre de la marche à l'intérieur de la cellule - Mise en évidence de la hauteur du film

Sur la figure 5 nous voyons nettement la marche et donc la différence de hauteur du film sur les deux parties de la cellule. Sa hauteur est plus grande, à gauche de la photo, lorsqu'il traverse l'épaisseur e₂ = 16,7 mm et plus petite lorsqu'il traverse l'épaisseur e₁ = 7,7 mm. Au premier ordre, dans les deux parties de la cellule, le film est à peu près vertical mais juste au niveau de la marche, il y a une petite déformation.

Nous observons que le film ne forme pas une ligne droite entre les deux plots, mais il marque un angle au niveau de la marche. Et, lorsque nous déplaçons le plot mobile, il apparait que l'angle et la position du film savonneux dans les deux parties de la cellule se modifient, vidéo figure 6.

Nous précisons que, dans la suite de l'étude, nous ne considérons que la modification de l'angle une fois le film de savon en position d'équilibre. En effet, ici, on ne s'intéresse pas à l’analyse de la dynamique d'établissement du film. Ainsi, les points expérimentaux déterminés par la suite correspondent à un point expérimental de position du plot, lorsque le film est à l'équilibre.

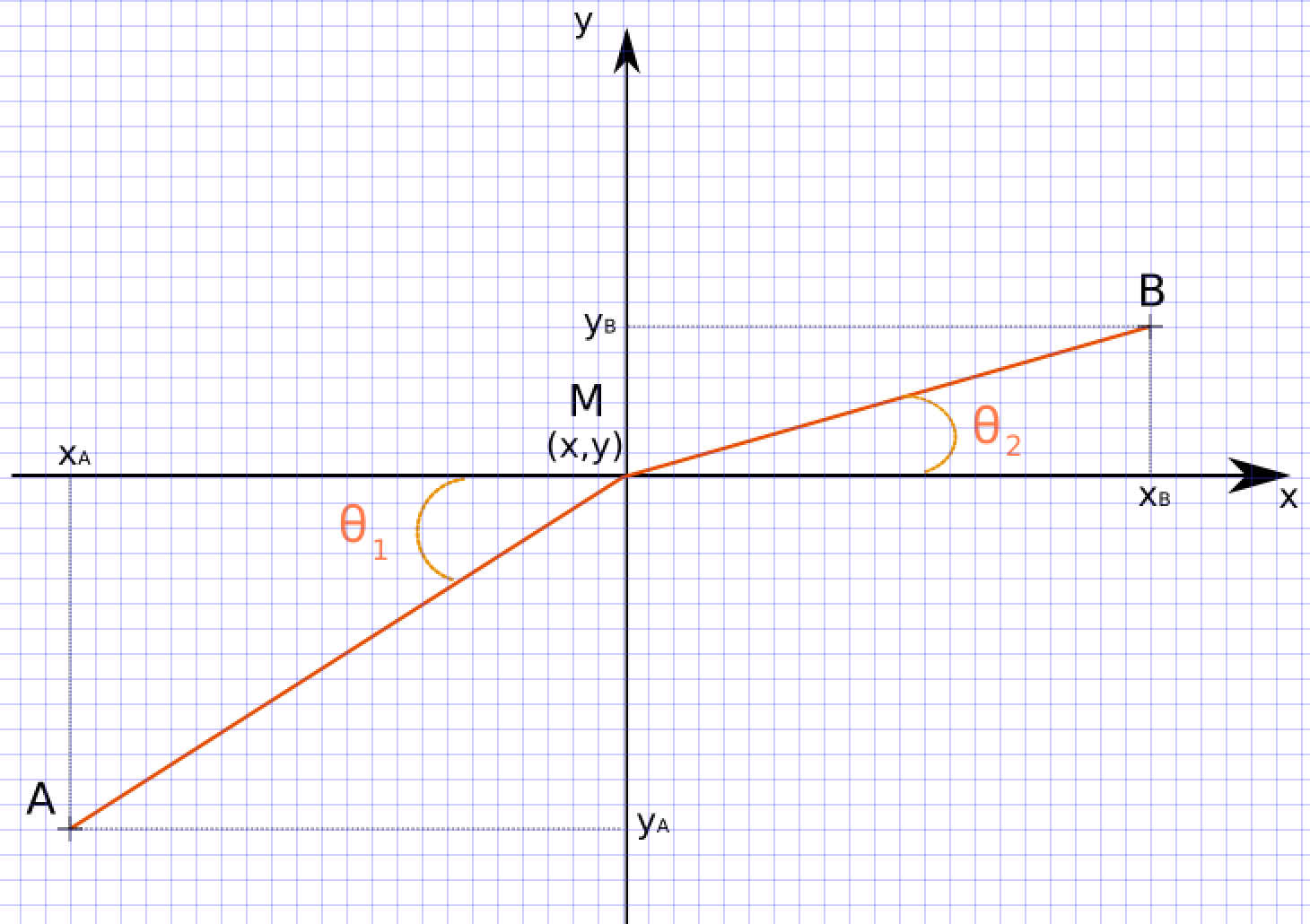
Afin de comprendre les phénomènes physiques sous-jacents derrière le changement de géométrie du film savonneux, nous allons commencer par mesurer les angles θ₁ et θ₂ formés par le film de savon, de part et d'autre de la marche, avec la normale à l'interface, figure 7.

Nous mesurons les angles à l'aide d'un rapporteur, figure 8. Notons que, comme la ligne de position de la marche donne une référence visible alors que notre référence en pointillée horizontale n'est pas visible, pour déduire la valeur de θ₁, nous mesurons π/2 + θ₁.

Figure 7.  Caractérisation des angles θ1 et θ2 formés de part et d'autre de la marche

Figure 8. Mesure des angles θ1 et θ2 et valeur de leur sinus correspondant

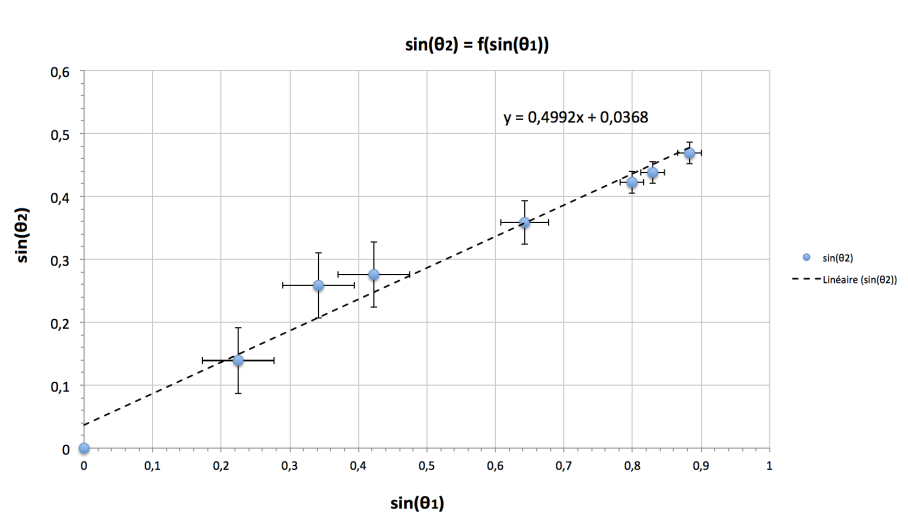
Sur la figure 9, nous avons représenté sin(θ₂) en fonction de sin(θ₁). En ajoutant à l'ajustement le point (0,0) (car sin(0) = 0), nous obtenons une droite dont le coefficient directeur est environ 0,49.

Figure 9.  Représentation graphique de \(\sin(\theta_2)\) en fonction de \(\sin(\theta_1)\) et ajustement des données

Pour interpréter ce résultat, il faut rappeler que le film de savon va chercher à minimiser son énergie, c'est-à-dire minimiser sa surface.

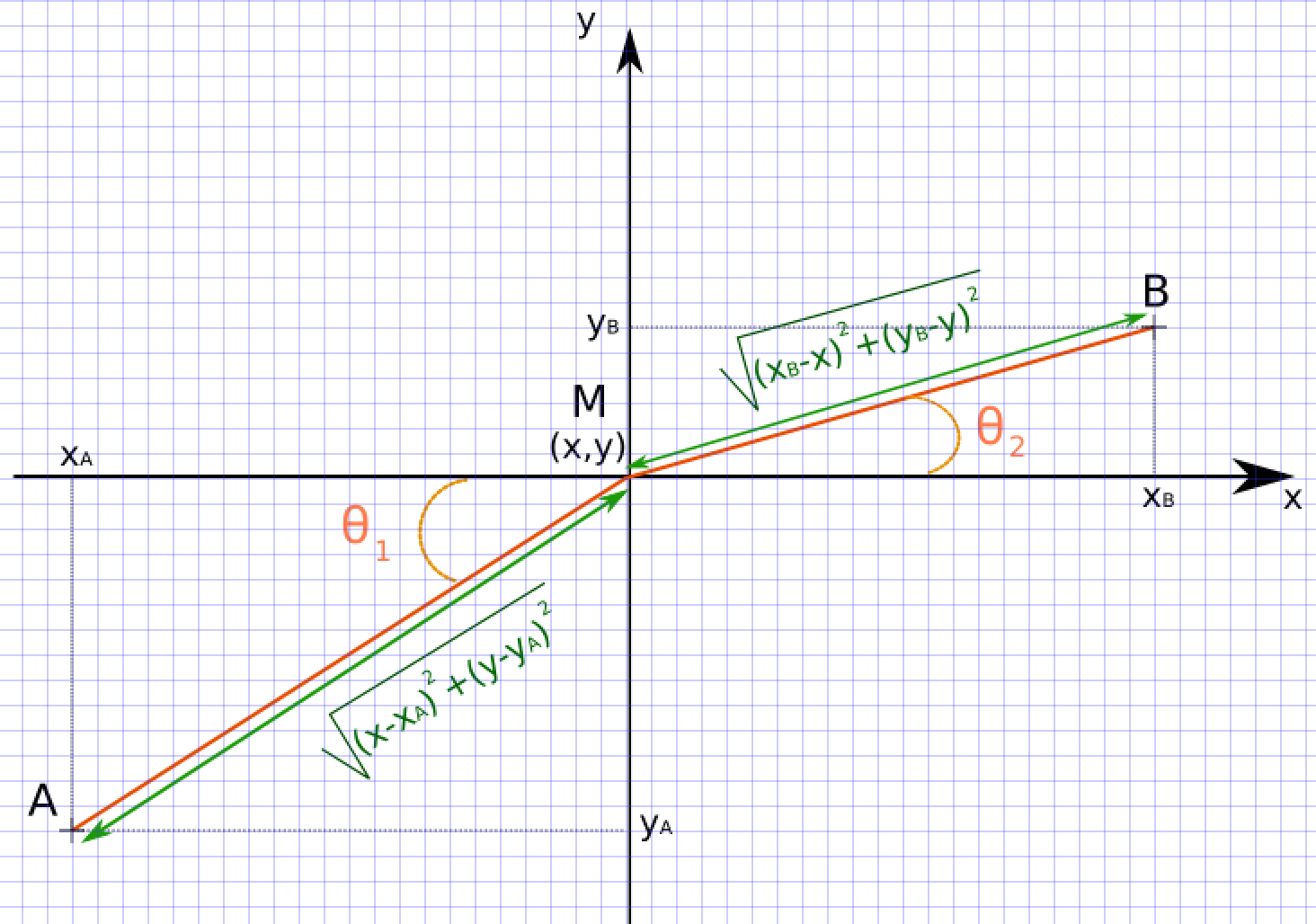
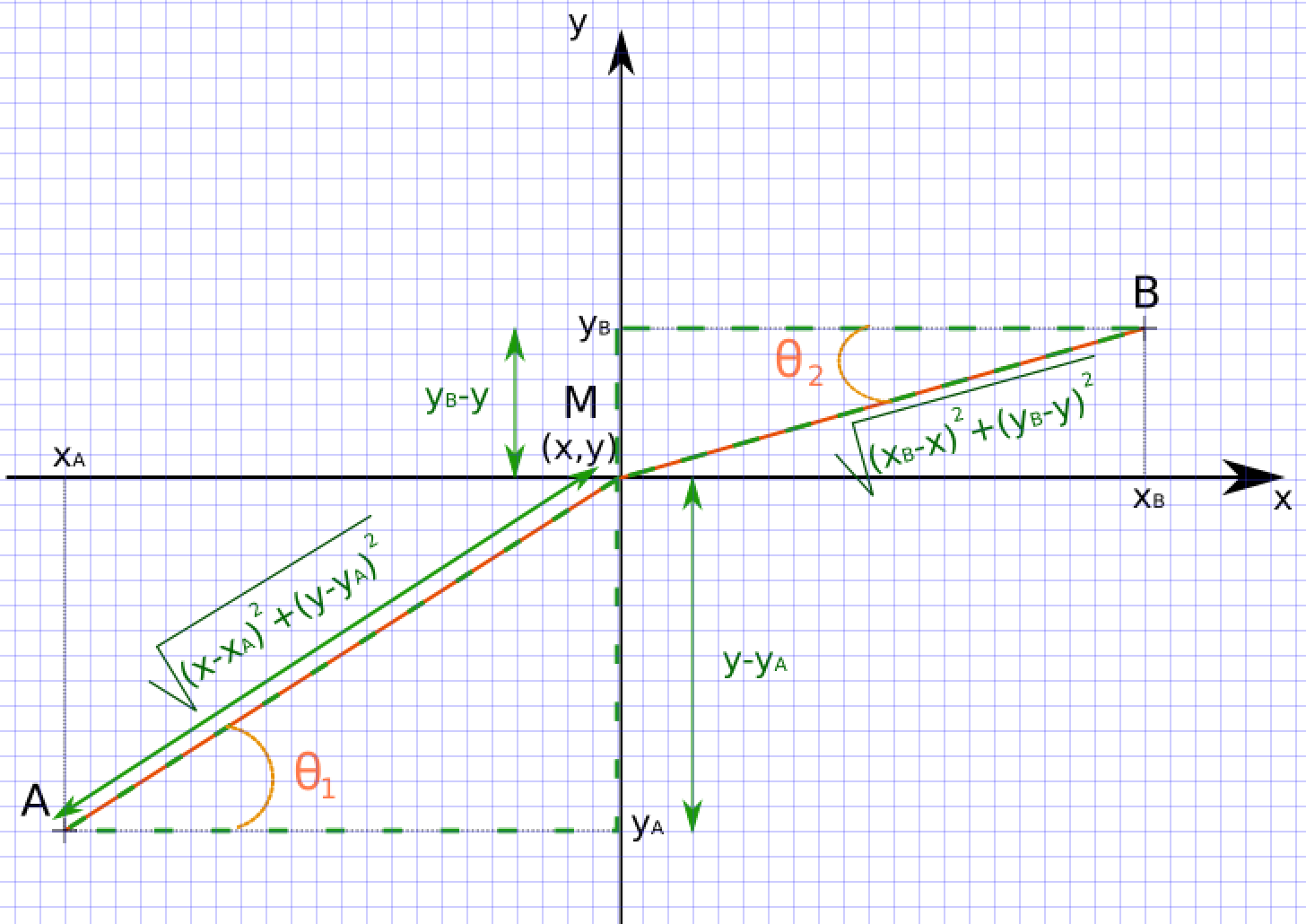
On note M le point d'intersection entre les deux épaisseurs. Il a pour coordonnées M (x,y), et les points A (x_A,y_A) et B (x_B,y_B), figures 10 et 11.

L'abscisse x du point M est déterminée, puisqu'elle correspond à la position de la marche. On aurait pu la noter x = 0. Par contre, l'ordonnée y du point M est différente pour chaque position du film de savon.

Figure 10.  Représentation de l'aire du film de savon dans la cellule

Figure 11.  Schéma représentant la position des points M, A et B

L'aire du film de savon est donc égale à (figure 12) :

Figure 12.  Schéma représentant les longeurs du film de savon de part et d'autre de la marche

Maintenant, compte-tenu de la condition de minimisation de l'aire du film de savon, on cherche à minimiser l'équation obtenue. La composante x étant fixée (située au niveau de la marche, comme nous l'avons vu plus haut), on minimise l'aire par rapport à la seule composante variable : y. Ainsi :

Ce qui peut s'écrire (à l'aide de la figure 13) comme :

Figure 13.  Schéma représentant les longueurs du film de part et d'autre de la marche en utilisant les relations trigonométriques

Et on retrouve :

avec

Expérimentalement, la mesure nous avait donné (figure 9) : $\genfrac{}{}{0.1ex}{}{\sin \left({\theta }_2\right)}{\sin \left({\theta }_1\right)}\approx \mathrm{0,49}$

En prenant en compte les incertitudes sur les mesures des angles, nous trouvons des droites d'ajustement dont le coefficient directeur varie de ±3 centièmes. La valeur théorique de 0,46 appartient donc à l'intervalle de confiance.

Ainsi le film de savon "préfère" passer plus de temps dans la région la plus fine (e₁) que du côté le plus large (e₂) pour minimiser son aire.

Ce phénomène est analogue avec la réfraction de la lumière à l'interface de deux milieux d'indices différents et suit la loi de Snell-Descartes.

En effet, il s'agit formellement du même phénomène. Le principe de Fermat, appelé aussi le principe du moindre temps, énonce que la lumière se propage entre deux points selon la trajectoire qui minimise son temps de parcours. Le temps de parcours de la lumière dans deux dioptres est \(t = \frac{d}{v}\), avec d la distance et \(v\) la vitesse. Or la vitesse est directement reliée à l'indice : \(v_i = \frac{c}{n_i}\) où \(c\) est la vitesse de propagation de la lumière dans le vide et \(n\) l'indice du milieu \(i\). Les rayons lumineux minimisent donc la distance parcourue dans le milieu d'indice supérieur.

On peut encore donner une analogie très parlante. Prenons un sauveteur côtier qui doit partir de la plage pour sauver quelqu'un dans l'eau. Intuitivement, il sait qu'il doit courir le plus longtemps possible sur la plage car sa vitesse est beaucoup plus grande que celle qu'il aura lorsqu'il se déplacera dans l'eau.