Activer le mode zen
Ressource au format PDF
Mots-clés
- réflexion
- réfraction
- dioptre
- lentille
- miroir
Classification
Le labyrinthe optique
16/01/2023
Résumé
Cet article propose un dispositif expérimental pour retrouver les lois de l'optique géométrique et répondre à des défis, de manière ludique, en utilisant du matériel simple (miroirs, lentille, prisme…).
Table des matières
Introduction
Les manipulations proposées ici sont tirées d'une activité proposée à l'Experimentarium de physique de l'Université Libre de Bruxelles [1]. Ce lieu propose des installations qui parcourent notamment les grands thèmes et domaines de la physique : mécanique, optique, électrostatique, électromagnétisme, ondes, sans formalisme mathématique et avec souvent un côté ludique.
1. Le dispositif
Cette activité propose un moyen de sensibiliser les élèves aux lois de l'optique à base d'expérimentations. Le « labyrinthe optique » consiste en des manipulations d'objets classiques de l'optique : miroirs, lentilles, prisme, lames à face parallèles, réseaux… afin d'en observer les effets sur un faisceau de lumière.
Le matériel est simple et rudimentaire : une boite, un pointeur laser ou une diode laser, une tige de verre et les éléments d'optique à étudier, figures 1 et 2.
Nous utilisons ici une boite en bois, dans laquelle nous venons percer quatre portes, une sur chacun de ses côtés.
Figure 1. La boite du labyrinthe optique | Figure 2. Éléments optiques utilisés 2 miroirs plans, 2 prismes, 2 lentilles minces (une convergente et une divergente), 2 demi-cylindres, 1 lame-mince, 2 diapositives de réseaux. |
Sur la porte qui servira d'entrée, nous fixons une tige de verre en guise de lentille cylindrique. Lidée est de transformer le faisceau filiforme du laser en un faisceau demi-plan pour rendre visible le chemin lumineux sur le fond de la boite, figure 3.
2. Jouons au labyrinthe optique ! Défis expérimentaux
Dans la version proposée à l'Expérimentarium de Bruxelles, on donne une consigne aux joueurs et à eux de disposer les éléments d'optique pour répondre à chaque cas. Par exemple :
Pour chacun des défis, la lumière entre toujours par la porte d'entrée.
- En utilisant un seul miroir plan, faites sortir la lumière par une porte de côté.
- En utilisant deux miroirs plans, faites sortir la lumière par une porte de côté ou la porte du fond.
- En utilisant deux miroirs plans, dessinez à l'aide des faisceaux laser, un triangle rectangle et faites sortir la lumière par une porte de côté.
- En utilisant trois miroirs plans, dessinez à l'aide des faisceaux laser, un triangle isocèle et une de ses bissectrices et faites sortir la lumière par une porte de côté.
- En utilisant le prisme, faites sortir la lumière par une porte de côté, puis par deux portes.
- En utilisant le prisme et un miroir plan, faites sortir la lumière par deux portes.
- En utilisant une lentille, faites sortir la lumière par la porte du fond.
- …
3. Retrouver les lois
En jouant avec les éléments optiques, il est aussi possible de retrouver les lois de l'optique géométrique, par exemple en prenant en photo avec un smartphone, les expériences précédentes. C'est ce que nous proposons dans cette section.
Nous mettons à disposition toutes les images sources pour chaque cas de figure.
3.1 Réflexion sur un miroir plan
À l'aide du traitement d'image du logiciel Image J [2], il est par exemple possible de retrouver :
- Les lois de Snell-Descartes pour la réflexion.
Les figures 3 et 4 correspondent à l'image puis son analyse d'une réflexion sur un miroir plan.
Figure 4. Réflexion sur un miroir plan Accéder à la photo de la réflexion sur un miroir | Figure 5. Mesure de l'angle d'incidence et de l'angle réfléchi à l'aide du logiciel Image J Les angles 1 et 2 correspondent respectivement à l'angle d'incidence et l'angle réfléchi sur le miroir plan. Accéder à l'image de réflexion sur un miroir plan, travaillée sous Image J, pour la mesure des angles. |
Dans le logiciel Image J, la fonction de détection de seuil Find Edges dans le menu Process du logiciel, permet de mettre en évidence l'élément optique et les faisceaux.
On peut ensuite procéder de différentes façons. L'outil "trait" donne accès directement à son inclinaison dans le haut de la fenêtre.
Sinon on peut tracer le repère grâce à l'outil "trait" et on le fixe sur l'image (Draw dans le menu Edit). Le repère correspond à l'axe de l'élément optique et sa perpendiculaire (normale à l'interface, obtenue avec la fonction rotate du menu de sélection). À l'aide du repère et de la marque des faisceaux, on utilise l'outil de mesure d'angle pour déterminer les angles d'incidence et réfléchi.
Il est important de noter les sources d'erreurs qui entachent les résultats et qui proviennent de plusieurs sources : l'angle de prise de vue (la photo n'est pas forcément prise à la verticale) et introduction de parallaxe, le tracé du repère sur la photo (possibilité d'erreur de positionnement), la difficulté à placer le curseur finement pour la mesure des angles. C'est un bon exemple pour aborder les incertitudes de mesure !
On peut aussi travailler sur une configuration à deux miroirs, figures 6 et 7.
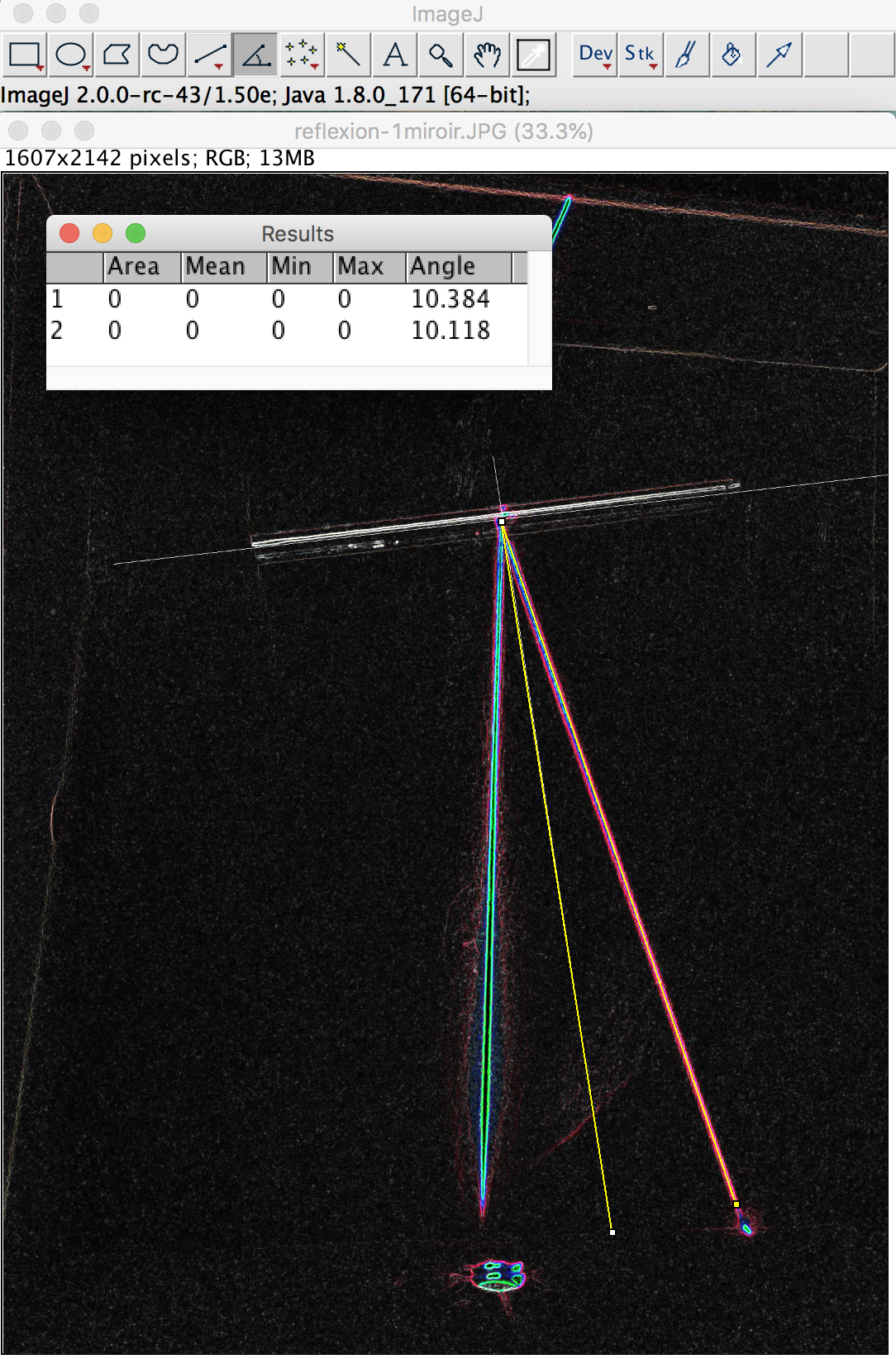
Figure 6. Réflexions sur deux miroirs plans Accéder à la photo de la réflexion sur deux miroirs plans | Figure 7. Mesure des angles d'incidence et réfléchis sur les 2 miroirs à l'aide du logiciel Image J Les angles 1 et 2 correspondent respectivement à l'angle d'incidence et l'angle réfléchi sur le miroir du haut de l'image. Les angles 3 et 4 correspondent respectivement à l'angle d'incidence et l'angle réfléchi sur le miroir du bas de l'image. Accéder à l'image de réflexion sur deux miroirs plans, travaillée sous Image J, pour la mesure des angles. |
3.2 Réflexion et réfraction - prisme ou demi-cylindre
En utilisant un prisme ou un demi-cylindre, on peut aussi retrouver :
- Les lois de Snell-Descartes pour la réflexion, sur la première interface, et la réfraction due au changement de milieu.
On utilise les mêmes outils que précédemment avec le logiciel Image J.
Pour le prisme, figures 8 à 11 :
Figure 8. Réflexion sur une face d'un prisme Accéder à la photo de la réflexion sur une face d'un prisme | Figure 9. Tracé du repère sur le prisme par le logiciel Image J Accéder à l'image de la réflexion et de la réfraction sur le prisme, travaillée sous Image J, pour la mesure des angles. |
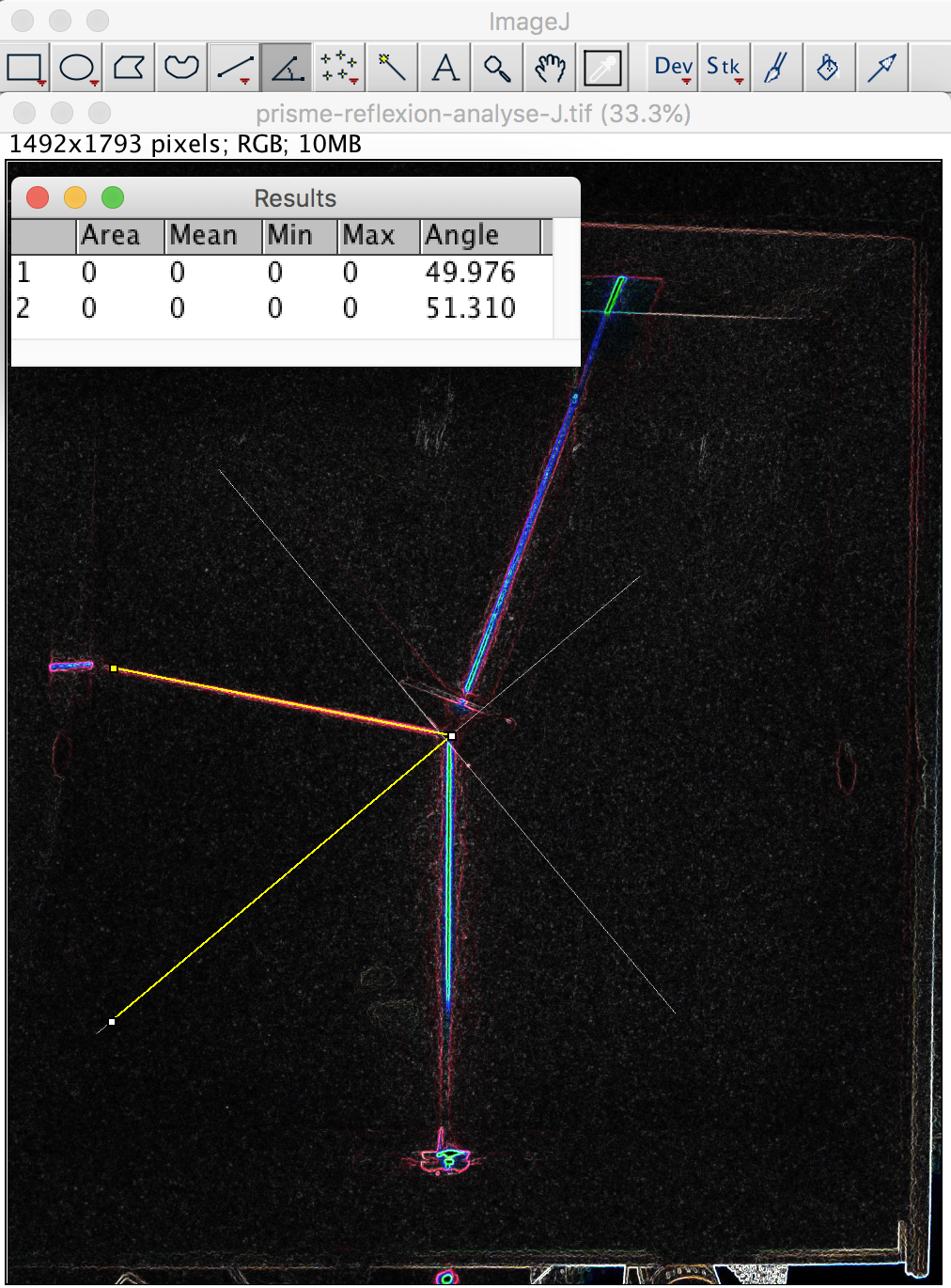
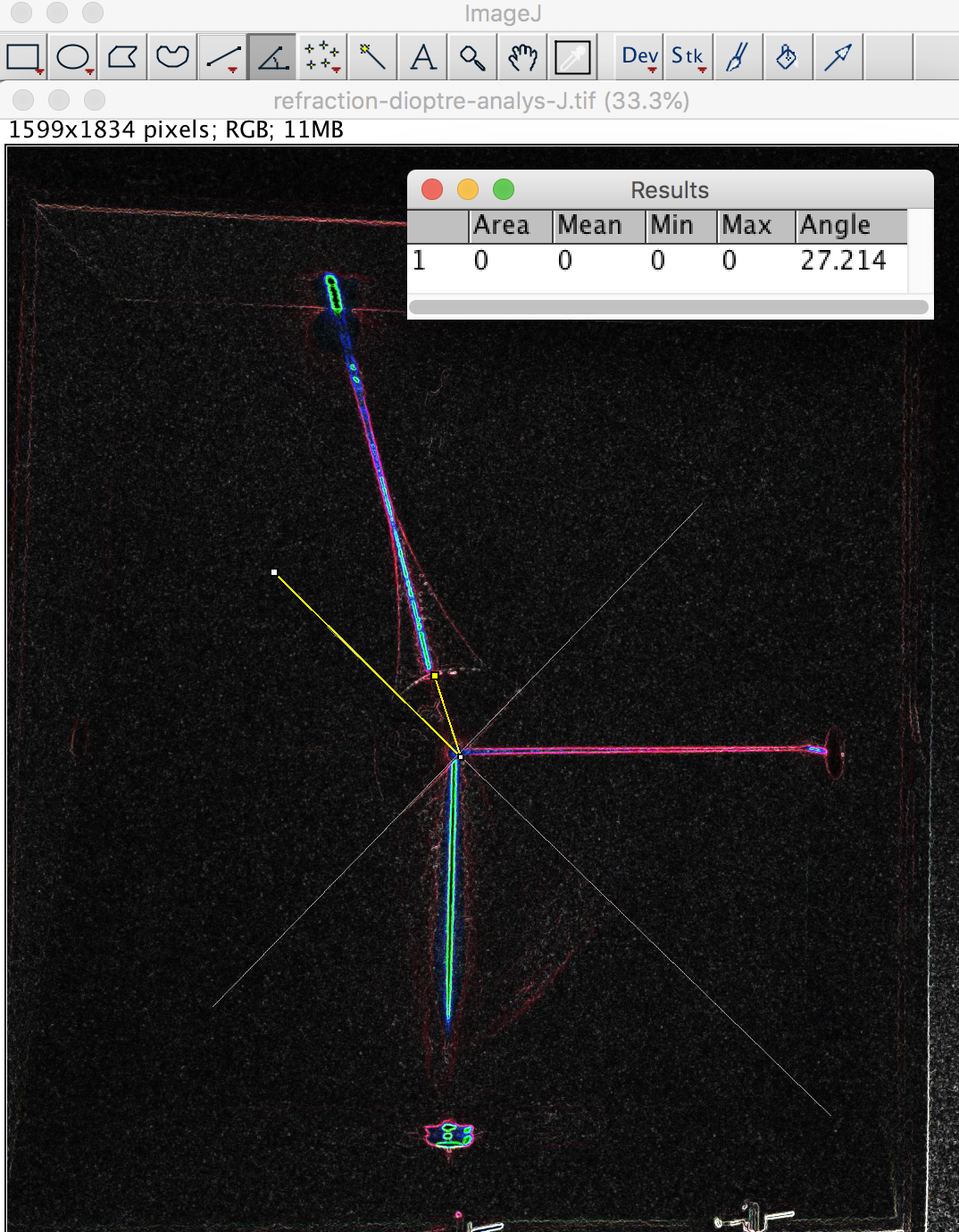
Figure 10. Mesure des angles d'incidence et réfléchi sur une face du prisme à l'aide du logiciel Image J Les angles 1 et 2 correspondent respectivement à l'angle d'incidence et l'angle réfléchi sur une face du prisme. Accéder à l'image de réflexion sur une face du prisme, travaillée sous Image J, pour la mesure des angles. | Figure 11. Mesure de l'angle de réfraction pour le prisme à l'aide du logiciel Image J, interface air/verre Accéder à l'image de réfraction par le prisme, travaillée sous Image J, pour la mesure des angles. |
Si l'on prend l'indice optique de l'air \(n_{air}\) = 1 et les angles mesurés, on trouve pour l'indice optique du prisme en verre \(n_{verre} =n_{air} \frac{\sin \theta_{air}}{ \sin \theta_{verre}}\approx\) 1,54.
On peut aussi mesurer les angles des rayons réfléchi et réfracté par un demi-cylindre en verre, figures 12 à 15.
Lorsque le rayon lumineux incident passe par le centre du demi-cercle (dioptre plan figure 12), le rayon réfracté dans le verre est perpendiculaire à l'interface verre/air de sortie du demi-cylindre, il n'est pas dévié en ce point.
Figure 12. Réflexion et réfraction par un demi-cylindre, interface air/verre Accéder à la photo de la réflexion et de la réfraction par un demi-cylindre | |
Si l'on prend l'indice optique de l'air \(n_{air}\) = 1 et les angles mesurés, on trouve pour l'indice optique du demi-cylindre en verre \(n_{verre} =n_{air} \frac{\sin \theta_{air}}{ \sin \theta_{verre}}\approx\) 1,56.
Dans le cas que nous venons d'étudier la lumière provient de la source située dans l'air pour entrer dans un milieu en verre. Mais la propagation dans le sens inverse est aussi possible. On peut ainsi mettre en évidence le phénomène de réflexion totale propre à cette configuration. Dans les figures 16 à 21, on s'intéresse à l'interface verre/air, le rayon incident étant dans le verre. On augmente l'angle d'incidence, en faisant pivoter le demi-cylindre. On observe que le faisceau réfracté, donc transmis devient plus faible et le faisceau réfléchi plus intense. À partir d'une certaine valeur d'angle d'incidence, l'angle limite, toute la lumière tombant sur l'interface verre/air est réfléchie et le rayon réfacté n'est plus transmis. La réflexion totale se maintient pour tout angle d'incidence supérieur à l'angle limite.
Le rayon lumineux lumière frappe maintenant d'abord le dioptre cylindrique du demi-cylindre. Il arrive sous incidence normale donc il traverse ce dioptre sans être dévié.
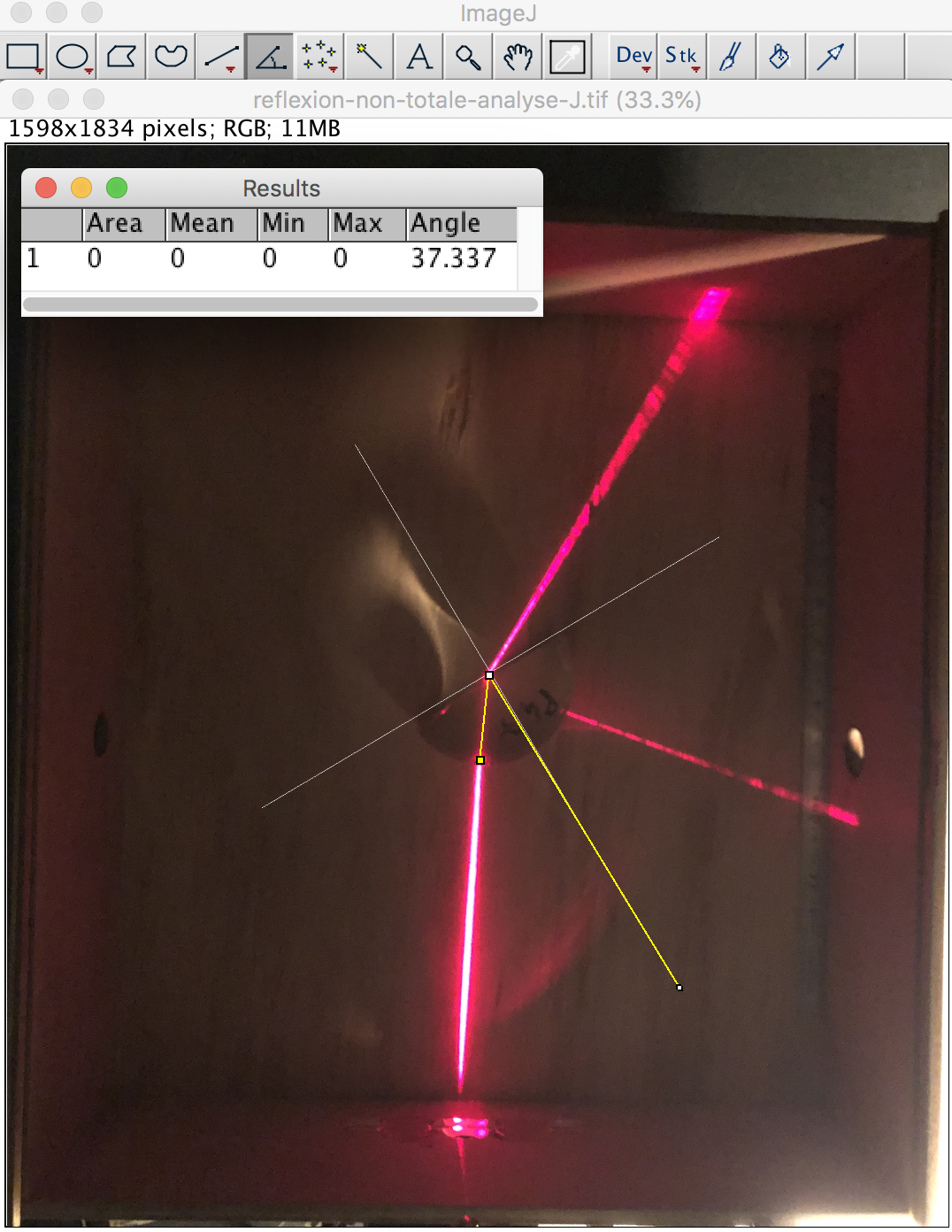
Figure 16. Réfraction et réflexion sur un demi-cylindre, interface verre/air Accéder à la photo de la réfraction et réflexion sur un demi-cylindre | Figure 18. Réflexion totale sur un demi-cylindre, interface verre/air Accéder à la photo de la réflexion totale sur un demi-cylindre pour un angle supérieur à l'angle limite | |
Figure 19. Réfraction et réflexion sur une demi-cylindre, interface verre/air L'angle d'incidence sur l'interface verre/air est d'environ 37°. | Figure 20. Réflexion totale sur un demi-cylindre pour l'angle limite, interface verre/air L'angle d'incidence sur l'interface verre/air est d'environ 40°, cela correspond à l'angle limite. | Figure 21. Réflexion totale sur un demi-cylindre - l'angle d'incidence est supérieur à l'angle limite L'angle d'incidence sur l'interface verre/air est d'environ 56°. |
On rappelle que l'angle limite pour l'interface verre/air varie, en général, entre 36° et 43° selon le type de verre utilisé.
On pourra aussi retrouver l'angle limite pour un prisme, figure 22 :
Figure 22. Réfraction et réflexion avec prisme, interface verre/air Accéder à la photo de la réfraction et réflexion sur une face du prisme, interface verre/air | Figure 23. Réflexion totale par un prisme, angle limite, interface verre/air Accéder à la photo de la réflexion totale sur une face du prisme, interface verre/air |
3.3 Lentilles
- A l'aide d'une diapositive de réseaux (par exemple 140 traits par mm), il est aussi possible de trouver les foyers de lentilles convergente et divergente.
En ajoutant une règle graduée dans la boite, pour étalonner les dimensions de la photo, on peut déterminer cette distance focale.
On s'intéresse à une lentille mince convergente, figure 24. Le réseau diffracte le faisceau et on va se servir des multiples faisceaux qui arrivent sur la lentille pour déterminer son foyer objet.
Lorsque l'on déplace la lentille dans la boite en l'approchant ou en l'éloignant de la source, l'ensemble des faisceaux divergent ou convergent. Lorsque la source est placée sur le foyer de la lentille, tous les faisceaux ressortent parallèles, figure 24.
Figure 24. Détermination du foyer d'une lentille convergente Accéder à la photo du montage s'intéressant à la lentille convergente |
Sur cette manipulation, nous serons prudents sur les résultats des mesures car les éléments sont déplacés à la main sans le guide d'un rail optique. Il faut aussi prendre en compte l'incertitude sur la détermination du parallélisme et la lecture de la mesure.
On peut ensuite se servir de cet ensemble de faisceaux parallèles pour déterminer le foyer image de la lentille divergente, figures 25 et 26.
Figure 25. Détermination du foyer d'une lentille divergente Accéder à la photo du montage s'intéressant à la lentille divergente |
Sur la figure 26, à l'aide du logiciel Image J, on vient prolonger les rayons semblants provenir du foyer image de la lentille divergente.
4. Boite mystère
Il est encore possible de jouer avec une boite fermée pour deviner ce qui compose le labyrinthe optique. On cherchera donc à trouver ce qu'il y a dans la boite et comment les éléments sont disposés. Pour cette utilisation, la tige en verre n'est plus nécessaire car la boite est fermée (nous n'avons plus besoin de voir la trace du faisceau au fond de la boite). La démarche consiste à éclairer successivement les différentes portes de la boite et de noter, dans chacun des cas, où ressort le faisceau lumineux.
On pourra, éventuellement, donner le nombre d'éléments présents dans la boite.
Références
[2] ImageJ, est un logiciel libre d'analyse et de traitement d'image.
Pour citer cet article :
Le labyrinthe optique, Philippe Léonard, Delphine Chareyron, janvier 2023. CultureSciences Physique - ISSN 2554-876X, https://culturesciencesphysique.ens-lyon.fr/ressource/labyrinthe-optique.xml