Le réfractomètre

On appelle réfraction le changement de direction que subit un rayon lumineux en passant d'un milieu optique donné à un autre. Ce changement est dû à une modification de la vitesse de propagation à partir du point, appelé point d'incidence, où le rayon lumineux incident frappe l'interface. Par analogie, on peut apparenter le phénomène de réfraction à la chute d'un nageur dans de l'eau suite à un plongeon. En effet, lors de sa rencontre avec le plan d'eau, sa vitesse diminue brusquement.

En réalité la totalité de la lumière ne pénètre pas dans le second milieu pour être réfracté ; une fraction subit le phénomène de réflexion. On suppose qu'il n'y a pas d'absorption. Sous certaines conditions que nous préciserons dans la suite, le faisceau peut subir une réflexion totale.

On appelle dioptre l'interface entre deux milieux d'indices optiques différents. Une vitre par exemple est constituée de deux dioptres. Une lentille est aussi constituée de deux dioptres non plans limitant une partie en verre... Les lois de Snell - Descartes indiquent ce que devient un rayon lumineux lorsqu'il traverse le dioptre en question.

L'indice n d'un milieu caractérise la vitesse de propagation de la lumière dans ce milieu. Plus précisément, pour une onde monochromatique, de longueur d'onde λ à température et pression fixées l'indice n d'un milieu est défini par le rapport entre la vitesse de la lumière dans le vide, notée c et celle mesurée dans ce milieu, notée v : n = c / v.

Pour la lumière visible et les milieux transparents, n est un réel supérieur à 1 et décroît avec un accroissement de la température ou lorsque la longueur d'onde augmente selon la formule empirique approchée de Cauchy :

n(λ) = A + B / λ² où A et B sont des constantes positives, spécifiques du milieu. Il s'agit en fait des premiers termes du développement limité de n en puissances paires de 1/λ.

Afin de préciser la température et la longueur d'onde considérées, on fait suivre l'indice de réfraction n d'un exposant représentant la température et d'un indice indiquant la nature de la radiation monochromatique de référence considérée. Dans la littérature, l'indice de réfraction est souvent donné à 20°C, à la longueur d'onde de référence de la raie D du sodium (589 nm), il s'écrit donc n_D²⁰.

Afin de ramener la valeur de l'indice de réfraction mesuré pour un liquide à une température T, en degré Celsius, à la valeur référencée à 20°C, on peut utiliser une relation affine valable pour de faibles écarts de température :

n²⁰ = n^T + 0,00045*(T-20) où T est la température exprimée en degré Celsius.

L'indice de réfraction d'une solution varie également en fonction de la concentration ou de la fraction molaire des constituants de la solution. Ceci peut être mis à profit pour déterminer la composition d'un mélange. Cependant, il faut au préalable tracer une droite d'étalonnage de l'indice de réfraction en fonction de la fraction molaire.

La pression est rarement mentionnée car elle a une influence moins importante que la température sur l'indice de réfraction des liquides. En effet, une augmentation de pression d'une atmosphère (soit de 1,013*10⁵ Pa) fait accroître l'indice de réfraction de 3*10^-5 ; alors qu'une augmentation de 1°C de la température fait décroître l'indice de réfraction de 4,5*10^-4. Par conséquent une faible variation de la pression atmosphérique produit un moindre changement de la valeur de l'indice de réfraction. Par ailleurs cet effet s'avère encore plus faible pour les solides.

On parle parfois de réfringence d'un milieu. Il s'agit d'une caractéristique liée à la valeur de l'indice n du milieu : plus l'indice est élevé, plus le milieu est réfringent.

Ces lois ont été énoncées par Snell et Descartes au XVII^ème siècle.

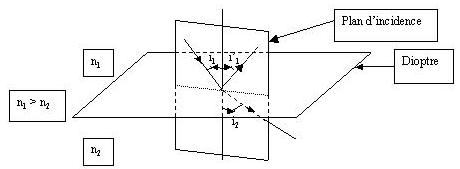
On considère un dioptre (interface entre deux milieux transparents homogènes d'indices optiques différents) séparant deux milieux homogènes et isotropes d'indices optiques respectifs n₁ et n₂. Soit un rayon lumineux arrivant sur ce dioptre en un point I appelé point d'incidence. On suppose que le milieu 1 est celui du rayon incident. Le plan contenant le rayon incident ainsi que la normale en I au dioptre est appelé plan d'incidence (voir figure 2 ci-dessous).

Figure 2. Réfraction, réflexion d'un rayon lumineux

Lois de Snell - Descartes :

Si le milieu 2 est plus réfringent que le milieu 1, donc si n₂ > n₁, alors i₂ < i₁ : le rayon dans le milieu le plus réfringent est plus proche de la normale au dioptre au point d'incidence que le rayon dans le milieu le moins réfringent.

Par ailleurs, il faut noter qu'il y a toujours une partie du rayonnement qui est réfléchie sur un dioptre.

En écrivant sin(i₂) = n₁/n₂ * sin(i₁) , on constate que si le rayon passe dans un milieu d'indice de réfraction plus élevé que celui dont il provient, son inclinaison par rapport à la normale au dioptre est diminuée. Inversement, quand il passe dans un milieu d'indice plus faible, son inclinaison est augmentée. Dans ce dernier cas, où n₁ est supérieur à n₂ , il existe alors un angle d'incidence limite i_{1 lim} égal à arcsin(n₁ / n₂) au-delà duquel il se produit nécessairement une réflexion totale, car le rayon réfracté ne peut plus exister.

Ce phénomène de réflexion totale est la base du principe de fonctionnement du réfractomètre.

Le terme de réfractomètre est principalement utilisé pour nommer des appareils qui permettent de déterminer l'indice de réfraction d'un liquide, bien qu'il existe également des instruments qui permettent la détermination de l'indice de réfraction d'un solide. Nous allons ici nous restreindre à la détermination de l'indice de réfraction des liquides.

Les réfractomètres les plus largement répandus d'Abbe et de Pulfrich mesurent l'angle de réfraction i₂ d'un rayon lumineux qui est relié à l'angle d'incidence i₁ selon les lois de Snell - Descartes. Le dioptre considéré ici est l'interface formée par la substance S dont on veut déterminer son indice de réfraction n_S et le prisme P qui a un indice de réfraction élevé n_P (voir figure 2).

D'après les lois de Snell - Descartes, l'indice de réfraction de la substance est défini ainsi : n_S = n_P * (sin(i₂) / sin(i₁)).

Cependant le problème d'obtenir exactement i₂ et i₁ s'avère considérablement simplifié en prenant un angle d'incidence égal à 90° (incidence rasante), puisque l'indice de réfraction de la substance S est plus faible que celui du prisme. En effet, d'après le paragraphe concernant la réflxion totale, nous avons mentionné que lorsque la lumière passe d'un milieu plus réfringent (indice le plus élevé) à un autre moins réfringent, l'angle d'incidence limite est celui qui correspond à un angle de réfraction de 90°. Selon le principe du retour inverse de la lumière, il va de soi que lorsque l'on passe d'un milieu moins réfringent, comme c'est le cas ici (n_S indice le plus faible) à un autre plus réfringent, l'angle de réfraction limite noté i_{2 lim} ou parfois appelé l'angle de réfraction critique noté i_2C est celui issu d'un angle d'incidence de 90°.

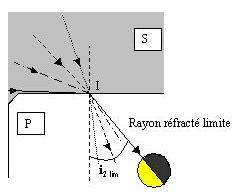
Sous une incidence rasante (figure 2), il y a donc un rayon réfracté limite tel que i_{2 lim} = arcsin (n_S / n_P) qui s'avère particulièrement facile à observer, car plus aucun rayon n'est réfracté dans le prisme P pour des angles plus grands que i_{2 lim}.

Figure 3. Frontière limite à l'intérieur du prisme du fait de la réfraction

Comme on peut le voir sur la figure 3, tous les rayons incidents entrant dans le prisme au point d'incidence I avec un angle compris entre 0° et 90° par rapport à la normale au point d'incidence I, sont réfractés dans une région angulaire du prisme définie d'une part par la normale et le rayon de réfraction limite défini précédemment. Ainsi l'angle limite de réfraction i_{2 lim} permet de définir une séparation ou frontière entre une zone claire (rayons réfractés) et une zone sombre (aucun rayon réfracté) à l'intérieur du prisme P.

En pratique, les conditions représentées sur la figure 3 sont quelque peu modifiées. La valeur de l'angle de réfraction limite i_{2 lim} n'est pas obtenue directement. En effet, pour observer la frontière entre la zone sombre et la zone claire explicitée précédemment, il s'avère indispensable d'utiliser un système optique tel qu'une lunette et un oculaire. Les rayons lumineux doivent donc traverser l'interface prisme - air, induisant ainsi un autre changement de direction des rayons lumineux au niveau de ce nouveau dioptre (voir figure 4 et tableau 2).

Figure 4. Rayon réfracté limite émergent du prisme

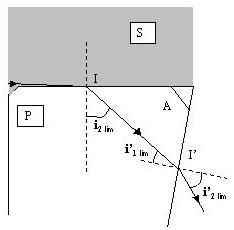
Le rayon lumineux qui provient d'un milieu d'indice inconnu n_S, et qui tombe sur le prisme d'indice n_P et d'angle au sommet A, sous une incidence rasante, émerge du prisme au point d'incidence I' en faisant un angle i'_{2 lim} avec la normale à la face de sortie du prisme.

D'après les lois de Snell-Descartes et les relations géométriques liées au prisme :

n_P * sin(i'_{1 lim}) = sin(i' _{2 lim})

et i'_{1 lim}= A - i_{2 lim}.

Finalement : sin(i' _{2 lim}) = n_P * sin(A - arcsin (n_S / n_P))

D'où on obtient : n_S = n_P * sin(A - arcsin (sin(i' _{2 lim}) / n_P))

Il découle de la relation précédente, que connaissant l'indice de réfraction du prisme considéré, et l'angle au sommet de celui-ci, on peut en déduire l'indice de réfraction n_S de la substance S en effectuant une détermination expérimentale de l'angle i' _{2 lim} formé entre la normale à la face de sortie du prisme et le rayon limite émergeant du prisme. Ceci se fait en repérant la limite entre la zone sombre et la zone claire observée à travers un oculaire d'une lunette lorsque l'on éclaire le système étudié sous une incidence rasante d'un faisceau lumineux monochromatique. Ces considérations peuvent s'appliquer et être utilisées pour des lumières ou sources polychromatiques (lumière blanche par exemple) ; elles s'avèrent légèrement modifiées. Cependant des modifications optiques internes au réfractomètre sont alors mises en oeuvre pour se ramener au cas simple de la longueur d'onde de référence de la raie D du sodium (589 nm).

Ainsi le système optique du réfractomètre est basé sur la mesure de l'angle de réfraction limite à l'interface d'un prisme d'indice de réfraction élevé en général de l'ordre de 1,7 et d'un liquide d'indice de réfraction inconnu n, inférieur à celui du prisme, que l'on souhaite déterminer expérimentalement.

Figure 5. Le réfractomètre vue du côté gauche	Figure 6. Le réfractomètre vue de face
Figure 7. Le réfractomètre vue du côté droit	Figure 8. Les deux prismes P et P'

L'appareil se compose :

Figure 9. Le réfractomètre vue du côté gauche	Figure 10. Le réfractomètre vue de face
Figure 11. Le réfractomètre vue du côté droit

Dans un premier temps, on effectue ces différentes opérations en regardant dans l'oculaire O (celui du bas) :

Une fois ces opérations effectuées, il suffit de regarder dans l'oculaire O'(celui du haut) et de lire la valeur de l'indice de réfraction sur l'échelle supérieure. En effet, deux échelles sont visibles : l'échelle supérieure ou à droite indique la valeur de l'indice de réfraction et l'échelle inférieure ou située à gauche, graduée de 0 à 85, donne en pourcentage la teneur en matières sèches des jus sucrés.

Figure 13. Aspect du champ de vision observable dans l'oculaire O

Figure 14. Échelles observables dans l'oculaire O'

Il est important de relever la température correspondant à cette mesure. Si le réfractomètre utilisé a un circuit de régulation de température des prismes et du thermomètre, la valeur de cette mesure est normalement identique à celle effectuée au cours des réglages préliminaires.

La précision de la mesure de l'indice de réfraction est de l'ordre de 10^-3, voire 10^-4, selon le type d'appareil utilisé.

Une fois la mesure effectuée, soulever le prisme mobile et essuyer une première fois, délicatement, les deux prismes avec du papier propre très doux (papier Joseph) ou du coton hydrophile propre imbibé d'alcool ou d'éther de pétrole selon la nature de l'échantillon, puis sécher avec un papier propre très doux et sec.

Une fois ceci effectué, rabattre doucement le prisme P' mobile. Il peut même être souhaitable d'interposer un morceau de papier Joseph sec entre les deux faces.