Activer le mode zen
Ressource au format PDF
Mots-clés
Classification
Physique et ingénierie des objets : le bilame
16/11/2020
Table des matières
Introduction
Le dossier « Physique et ingénierie des objets » est co-rédigé et co-publié avec le site Culture Sciences de l'ingénieur afin de proposer des ressources co-enseignées.
Cette ressource présente le bilame : son histoire, comment il est constitué, quelles sont ses fonctionnalités et ses propriétés. Des expériences simples et des exemples d’application sont proposés.
1. Qu'est-ce qu'un bilame ?
Un bilame, comme son nom l'indique, est un objet constitué de la juxtaposition de deux lames de matériaux différents. C'est grâce aux propriétés différentes de ces deux matériaux qu'il va être utilisé.
Sur les figures 1 à 6, nous proposons trois bilames différents afin d'observer leur comportement.
Source - © 2020 CultureSciences-Physique | |
Source - © 2020 CultureSciences-Physique Figure 4. On chauffe le bilame 2 | |
Figure 5. Bilame 3: bilame issu d'un thermostat | Source - © 2020 CultureSciences-Physique Figure 6. On chauffe le bilame 3 |
Dans la première expérience, nous avons réalisé un bilame en superposant un morceau de ruban adhésif sur un bout de papier. Lorsqu'on le plonge dans l'eau, on voit le bilame s'enrouler, le côté papier à l'extérieur. On réalise l'expérience test de mesure du même bout de papier (sans le ruban adhésif) avant et après être plongé dans l'eau, figure 7.
On constate que le papier s'est dilaté dans l'eau. Par contre, la taille du ruban adhésif reste la même. La dilatation d'un des côtés du bilame provoque une déformation de celui-ci.
De la même manière, lorsque le bilame 2 est chauffé, une de ses faces se dilate sous l'effet de la chaleur et il se courbe, figure 4.
La géométrie du bilame 3 est un peu différente. Il a la forme d'un disque courbé. Ainsi, en le chauffant, lorsqu'une de ses faces se dilate, sa courbure se renverse, figure 6. Une fois refroidi, il vient reprendre sa courbure initiale.
2. Retour historique sur l'apparition du bilame
2.1 Première utilisation connue du bilame
Historiquement, la première utilisation ou invention connue d'un bilame a été faite par l'horloger anglais John Harrison au XVIIIes [1]. Cet horloger a travaillé sur de nombreuses horloges et pendules et suite à un concours lancé pour mesurer le plus exactement le temps et repérer ainsi précisément les longitudes, lors des voyages en bateau, il a développé plusieurs prototypes de montres marines.
C'est lors de la création de son troisième chronomètre marin (H3), figure 8, en 1759, que John Harrison met en place un système de bilame pour compenser les effets de changements de température à bord [2]. Il est d'ailleurs remarquable de noter qu'avec son quatrième chronomètre (H4), figure 9, sur le trajet transatlantique, départ le 18 novembre 1761 de Grande Bretagne et arrivée le 19 janvier 1762 en Jamaïque [3], H4 affiche en retard de 5 secondes, soit une erreur de longitude de 1,25 minute, environ un mille marin (1 852 m).
(Source : Jonathan Betts, National Maritime Museum / Royal Observatory, Greenwich [2]) | (Source : Jonathan Betts, National Maritime Museum / Royal Observatory, Greenwich [2]) | (Source : Wikimedia) |
Plus tard, le capitaine James Cook utilisera une copie du chronomètre H4 lors de ses voyages dans le sud de l'Océan Pacifique.
En 2006, une plaque est installée à la mémoire de John Harrison dans Westminster Abbey avec, en son centre, un bilame sur lequel est noté la longitude, figure 10.
2.2 Intérêt du bilame dans les montres marines
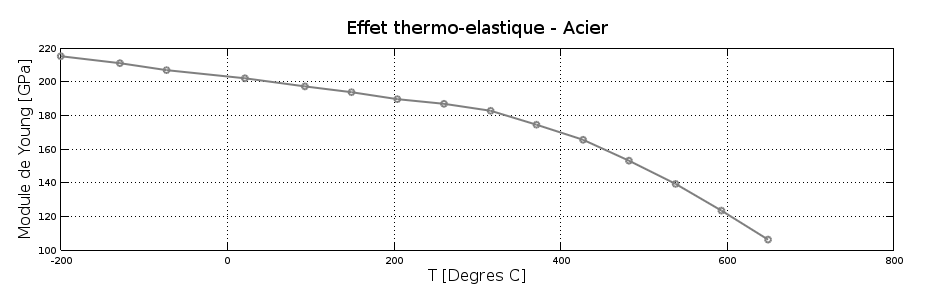
Au XVIIIes, les horloges sont souvent équipées d'un ressort spiral et d'un balancier en acier. On constate que l'horloge retarde lorsque la température augmente et qu'elle avance lorsque la température diminue car le module l'élasticité (ou module d'Young) du ressort spiral, augmente lorsque la température augmente, figure 11 [4].
L'effet d'une variation de température sur le module d'élasticité du ressort spiral en acier a un impact très important sur la marche de la montre. Un écart de +10°C provoque un retard de plus de 2 minutes par jour pour un système balancier/spiral non compensé.
(Source : SuisseMontre.com, Compensation des effets des variations de température sur la marche d'une montre [4]) | (Source : De quelle précision a-t-on réellement besoin en mer ?, Guy Boistel, Histoire et Mesure. [6]. D'après A. Ledieu, 1877, p. 326.) |
John Harrison utilise alors dans ses montres marines un ressort spiral bilame cuivre/acier. La courbure provoquée par la modification de température agit sur la longueur du ressort. Un ressort spiral plus long sera plus souple et entraînera un retard, compensant ainsi l'effet accélérateur de la baisse de température. À l'inverse, un ressort spiral plus court sera plus rigide et entraînera une avance compensant l'effet de retard de la hausse de température [4].
À la suite de John Harrison, en 1766, Pierre Le Roy et plus tard, John Arnold proposent une méthode de compensation de la température en jouant, cette fois, sur un balancier bimétallique. L'objectif est de modifier l'inertie du balancier lorsque la température varie afin de compenser les variations de la rigidité du ressort spiral en acier.
En 1862, l’astronome français Yvon Villarceau dans un « Mémoire sur le mouvement et la compensation des chronomètres », publié dans les « Annales de l’Observatoire », s’intéresse au mouvement du balancier ainsi qu'à la théorie du balancier bilame : compensation et réglage [5]. Il propose dans la foulée une nouvelle formule pour aider les navigateurs à corriger la marche des montres marines, figure 12 [6][7].
3. Mise en équation du phénomène
3.1 Déformation d'un unique matériau
Dans cette partie nous allons nous intéresser à la déformation d'une seule lame.
Afin d'étudier la déformation d'un bilame, nous proposons dans un premier temps de réaliser l'expérience témoin avec un seul matériau. Prenons comme premier exemple une feuille de papier que l'on vient déposer dans une bassine d'eau, figure 13.
Source - © 2020 CultureSciences-Physique |
Dans chacun des cas, on observe que la dilatation, soit due à l'absorption d'eau ou à l'augmentation de chaleur de chaleur, produit une déformation du côté du matériau en contact direct (ou le plus proche) de la source. Ensuite l'humidité, ou la chaleur s'uniformise et le matériau vient reprendre une forme plane. On voit donc une déformation transitoire du matériau.
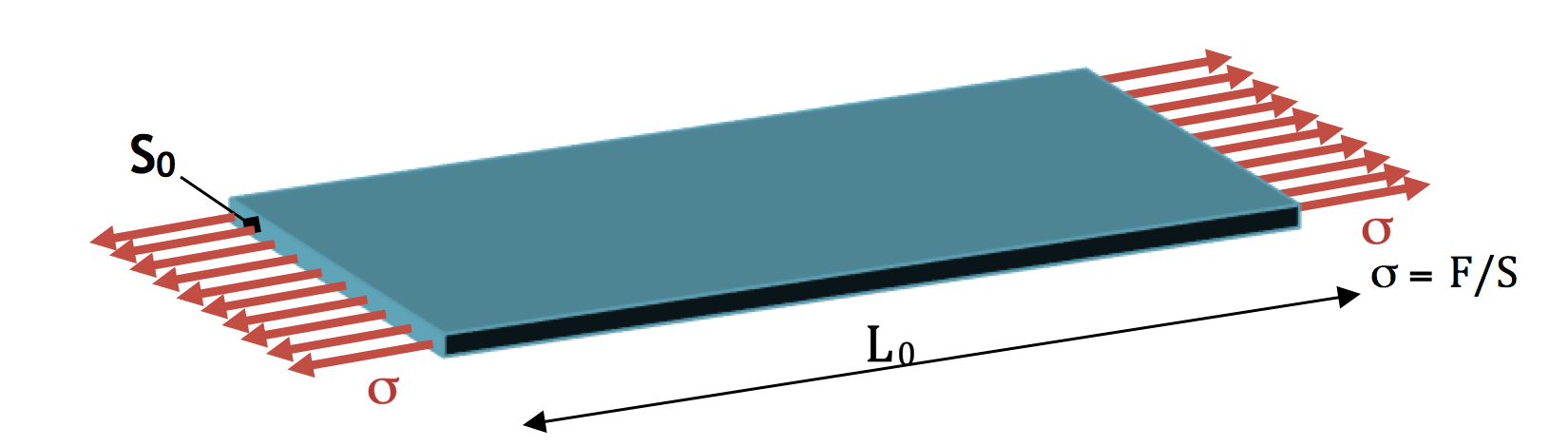
Considérons, figure 14, une poutre en matériau isotrope et homogène, sa longueur \(L_0 \) à la température \(T_0 \), s’accroit de \(\Delta L = L - L_0 \) si l’on augmente sa température de \(\Delta T = T - T_0 \) tel que :
$$\Delta L = \alpha L_0 \Delta T$$
Avec α le coefficient de dilatation linéaire du matériau à \(T_0 \).
Selon les hypothèses de la résistance des matériaux, nous considérons que les déformations sont faibles devant les dimensions de la poutre, la variation de section est négligeable et les sections planes normales à la ligne moyenne avant déformation le restent après déformation.
Dans la limite d'élasticité du matériau, la loi de Hooke s'exprime par :
$$\sigma = E \epsilon $$
Le module d'Young \(E \), ou module d'élasticité, est la grandeur qui relie la contrainte normale \(\sigma \) (étirement ou compression) subie par le matériau à la déformation élastique \(c \epsilon \) (allongement ou raccourcissement) qui en résulte [9].
$$\sigma = E \frac{\Delta L}{L_0} $$
La contrainte créée par l'élévation de température est ainsi proportionnelle au coefficient de dilatation et au module d'Young du matériau :
$$\sigma = E \alpha \Delta T $$
Lorsqu'on étudie les contraintes thermiques d'un volume, \(\sigma \) aura la forme d'un tenseur de contraintes.
3.2 Déformation d'un bilame
Un bilame est constitué de la juxtaposition de deux matériaux différents dont le coefficient de dilatation n'est pas le même, figure 15.
(D'après : Kanthal, [8]) |
Considérons, par exemple, le matériau 1, sa longueur \(L_0 \) à la température \(T_0 \), s’accroit de \(L-L_0 \) si l’on augmente sa température de \(T-T_0 \) tel que :
$$\frac{L-L_0}{L_0} = \alpha (T-T_0) $$
Avec \(\alpha \) le coefficient de dilatation linéaire du matériau à \(T_0 \).
Le module d'Young, ou module d'élasticité, est la grandeur qui relie la contrainte normale \(\sigma \) (étirement ou compression) subie par le matériau à la déformation élastique \(\epsilon \) (allongement ou raccourcissement) qui en résulte. Dans la limite d'élasticité du matériau, la loi de Hooke donne :
$$\sigma = E \epsilon $$
Avec l'allongement relatif $$\epsilon = \frac{L-L_0}{L_0} $$
Au sein du matériau, dans cet assemblage plus complexe, il se crée d'autres contraintes entre les deux matériaux. Ils se déforment collés l'un sur l'autre.
La contrainte créée par l'élévation de température est proportionnelle au coefficient de dilatation et au module d'Young du matériau :
$$\sigma = E \alpha (T-T_0) $$
L'analyse des contraintes et de la déflexion d'un bilame idéal ont été obtenues en 1865 par Yvon Villarceau [10][11].
L'équation générale donnant le rayon de courbure R d'un bilame plat uniformément chauffé d'une température T0 à T en l'absence de forces extérieures est donnée par :
$$\frac{1}{R}-\frac{1}{R_0} = \frac{3}{2} \frac{(\alpha_2 - \alpha_1) (T-T_0)}{1+\frac{(E_1 s_1^2 - E_2 s_2^2)^2}{4 E_1 s_1 E_2 s_2 s^2}} $$
Avec :
- \(R_0 \) le rayon de courbure initial à la température \(T_0 \) ;
- \(\alpha_1 \) et \(\alpha_2 \) les coefficients de dilatation des matériaux 1 et 2 (1 pour le matériau le moins extensible) ;
- \(E_1 \) et \(E_2 \) les modules d'Young des deux matériaux ;
- \(s_1 \) et \(s_2 \) les épaisseurs des deux matériaux ;
- \(s = s_1 +s_2 \) l'épaisseur du bilame.
Dans la plupart des applications industrielles, les bilames suivent des spécifications standards (DIN 1715 en Europe). Par exemple, l'épaisseur des deux matériaux est souvent la même (s1 / s2 = 1), et en prenant deux matériaux dont le module d'Young est presque le même (E1 / E2 ≈ 1), le calcul du rayon de courbure se simplifie :
$$ \frac{1}{R}-\frac{1}{R_0} \approx \frac{3}{2} \frac{(\alpha_2 - \alpha_1) (T-T_0)}{2 s} $$
On définit la flexibilité (ou courbure spécifique) par le facteur \(k \) :
$$k = \frac{3 (\alpha_2 - \alpha_1)}{2} $$
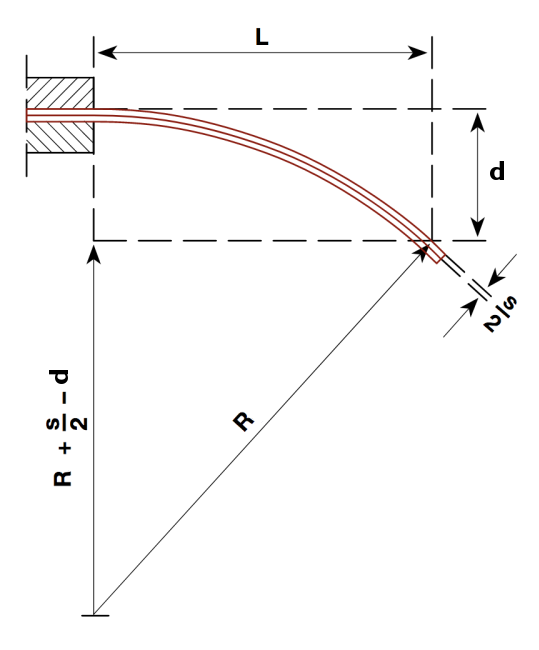
Pour un bilame plat, maintenu à une extrémité et sans courbure initiale à la température \(T_0 \), figure 16, on a :
$$ \frac{1}{R} = \frac{k (T-T_0)}{s} $$
(D'après : Kanthal, [8]) |
Pour trouver la déflexion d, on applique le théorème de Pythagore :
$$ (R + \frac{s}{2})^2 = (R + \frac{s}{2} - d)^2 +L^2 $$
En général, la déflexion du bilame est plus petite que 10% de sa longueur \(L \), on peut donc simplifier l'équation précédente en :
$$ d = \frac{k (T-T_0) L^2}{2s} $$
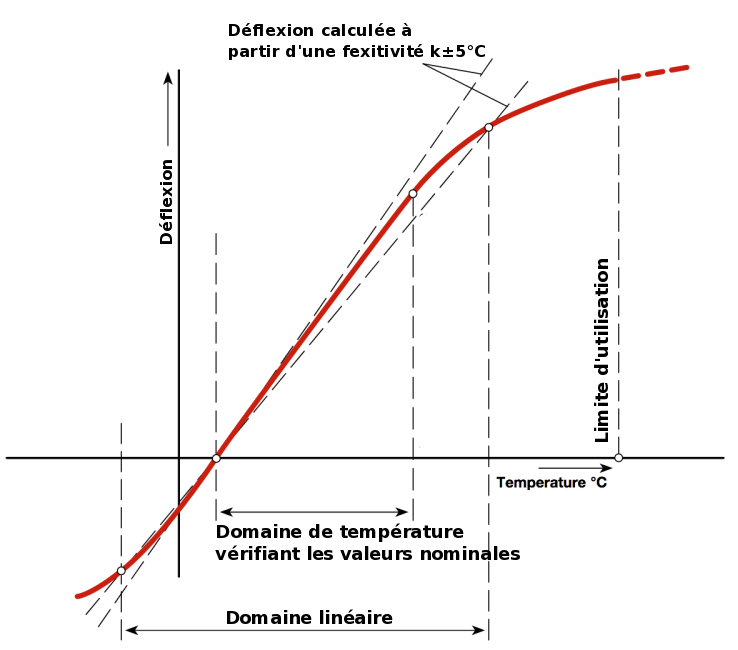
Un exemple de courbe de réponse d'un bilame est présenté sur la figure 17. On voit une zone pour laquelle la déflexion augmente linéairement avec la température. Selon les applications utilisant le bilame, il peut être intéressant d'avoir une sensibilité constante du système. Pour d'autres applications, le domaine d'utilisation peut être étendu jusqu'à une température limite qui correspond à la limite d'élasticité (provoquant une déformation permanente) d'un des composants utilisé.
(D'après : Kanthal, [8]) Figure 17. Déflexion en fonction de la température |
4. Propriétés des bilames
4.1 Résistivité
L'échauffement d'un bilame peut être créé par effet Joule. Dans ce cas on a besoin de bien connaitre la résistance du bilame.
La résistivité du bilame est donnée par :
$$ \rho = \frac{R S}{L} $$
Avec \(R \) la résistance mesurée (Ω), \(L \) la longueur du bilame (m) et \(S \) sa section (épaisseur × largeur) (m2)
4.2 Alliages
4.2.1 Retour au XIXe siècle
Encore une fois, ici, il est intéressant de faire un retour historique sur la recherche des matériaux utilisés.
Fils d'horloger, Charles-Edouard Guillaume (1861-1938) était un physicien suisse, figure 18. En 1883, il obtient un poste au Bureau International des Poids et Mesures (BIPM) à Sèvre près de Paris. Sa connaissance du monde horloger et des problématiques liées à la précision d'une montre le mène à poursuivre ses recherches sur les alliages fer/nickel. En effet il se souvient des observations de son père qui relevait que la bonne marche d'une montre sous différentes températures dépendait non seulement de la longueur du ressort spiral mais également de son élasticité [4].
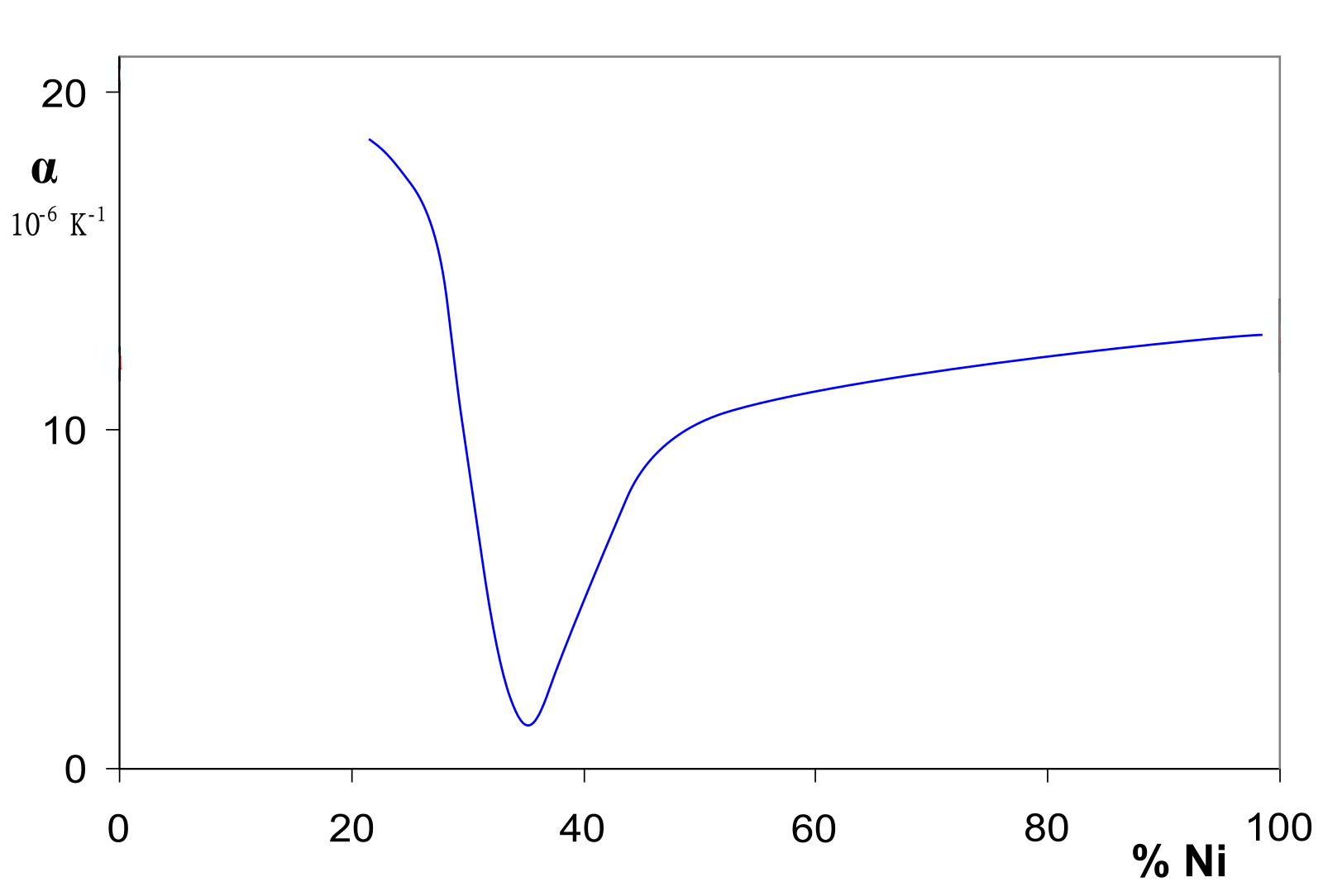
Il travaille sur des alliages constitués de fer et de nickel. Ces alliages présentent des anomalies intéressantes au niveau de leur coefficient de dilatation thermique. Il demande alors aux fonderies Commentry Fourchambault et Decazeville de lui fournir une barre fer 60% - nickel 30% et constate un coefficient de dilatation thermique environ 4 fois plus faible que celui du fer ou du nickel, figure 19. Il teste ensuite, avec le soutien de ces fonderies, plus de 600 variations de l'alliage Fer/Nickel.
En 1897 il publie un article montrant en particulier que l'alliage comprenant 36% de Nickel possède le coefficient de dilatation le plus faible, largement inférieur à celui du platine iridium (matière utilisée pour les étalons des premières "règles-étalons"). Cet alliage sera nommé Invar par Marc Thury (ingénieur et professeur originaire de Nyon) et il aura des applications immédiates dans la métrologie ainsi que pour la confection de balanciers de pendules [4][12].
La découverte de l'Invar vaut à Charles-Edouard Guillaume le prestigieux Prix Nobel de physique en 1920.
(Source : The Nobel Prize) | (Source : Wikimedia) |
4.2.2 Exemples de matériaux composants les bilames
L'Invar est très fréquemment utilisé en guise de matériau le moins extensible dans les bilames.
Le tableau 1 présente les différents matériaux, leurs caractéristiques physiques, leur dénomination pour des bilames couramment utilisés.
Tableau 1. Exemples de matériaux utilisés pour les bilames
Dénomination | Composition | Coefficient de dilatation (10-6°C-1) | Module l'élasticité (1012N.m-2) | Température limite de linéarité (°C) | Température limite d'emploi (°C) | Résistivité à 20°C (μΩ.cm) | Module d'Young à 20°C (1012N.m-2) | Conductivité thermique (W.m-1K-1) |
AS | Invar : Ni = 36%, Fe = 64% | 0,5 | 0,151 | 200 | 500 | 79 | 0,168 | 10,88 |
B6M : Ni = 20%, Mn = 6%, Fe = 74% | 20,4 | 0,198 | ||||||
R15 | Invar : Ni = 36%, Fe = 64% | 0,5 | 0,151 | 200 | 500 | 16,6 | 0,172 | 54,42 |
Nickel : Ni > 99,5%, Fe = solde | 13 | 0,22 | ||||||
SP 21 N | Invar : Ni = 36%, Fe = 64% | 0,5 | 0,151 | 200 | 350 | 112 | 0,136 | 7,63 |
Bilman : Mn = 74%, Cu = 10%, Ni = 16% | 29 | 0,118 |
5. Constitution, forme, matériaux
Les bilames sont produits par co-laminage de deux bandes de métal comme on peut le voir figure 20, les deux matériaux se trouvent ainsi solidarisés.
(D'après : Kanthal, [5]) Figure 20. Co-laminage à la société Kanthal |
L’étude théorique s’est principalement intéressée à un bilame plat à déformation continue, mais d’autres formes géométriques de bilames avec des conditions aux limites différentes permettent d’autres comportements, figure 21. Par exemple, les bilames sous forme de disques incurvés ont un comportement discontinu, la déformation macroscopique du bilame est brusque et instantanée (on les appelle justement bilames à retournement brusque). Certains bilames reviennent ensuite naturellement vers leur courbure initiale alors que d’autres restent dans leur nouvelle position.
On trouve encore des bilames en spiral ou hélicoïdaux. Tous les bilames ne sont pas forcément réversibles, on trouve, par exemple, des boitiers de bilame à retournement brusque, sur lesquels un bouton poussoir est placé afin de les ré-enclencher (retourner la courbure dans le sens initial).
(D'après : Kanthal, [5]) Figure 21. Différentes formes et boitiers de bilames |
6. Applications
Les bilames ont de multiples applications. Ils peuvent être utilisés pour donner une indication (mesure de la température), pour contrôler une installation (régulation, limiteur de temps) ou encore pour protéger des dispositifs électriques (interrupteur).
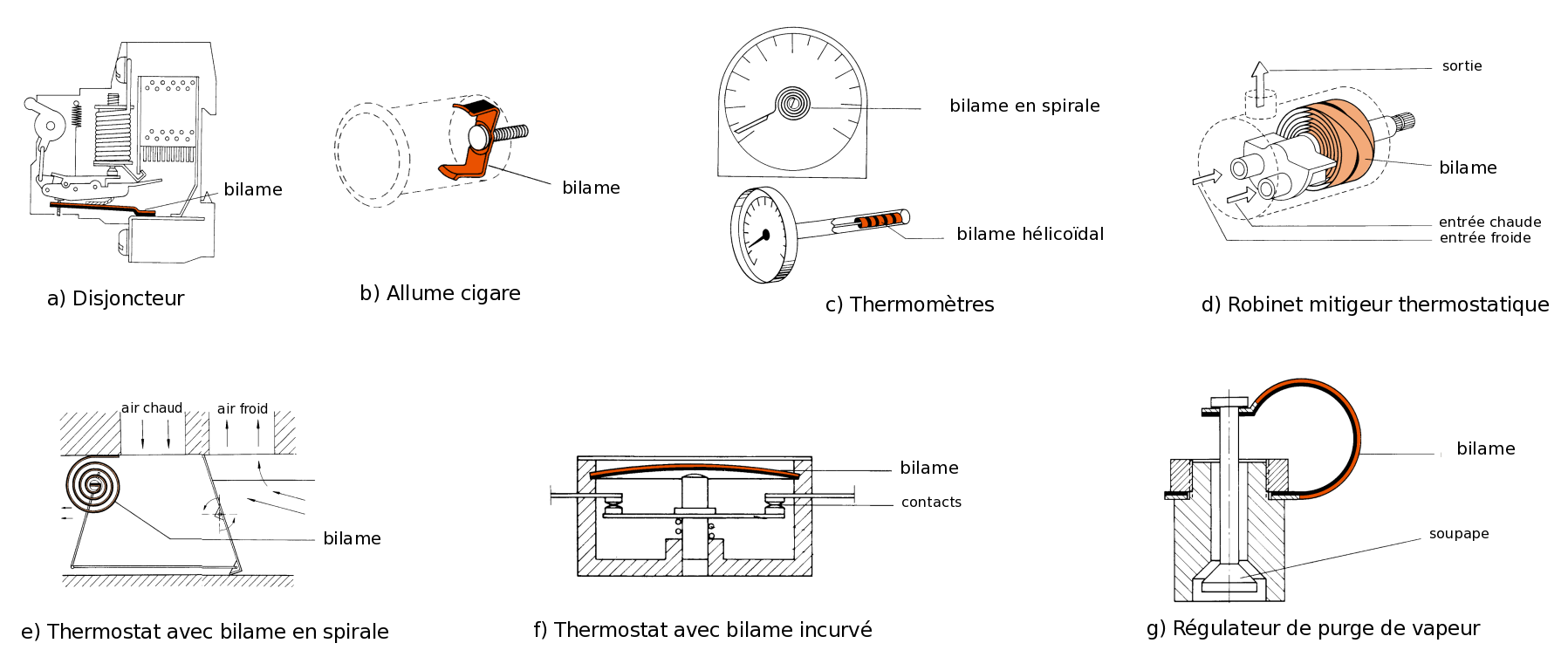
La figure 22 regroupe les croquis de différentes fonctionnalités : rôle d'interrupteur dans un disjoncteur thermique, limiteur du temps dans un allume cigare, mesure de la température, régulation de la température dans un robinet mitigeur thermostatique ou un système de ventilation, interrupteur dans une bouilloire électrique, ou encore régulateur de vapeur dans un système de purge.
(D'après : Kanthal, [5]) Figure 22. Différentes applications des bilames |
Les bilames plats et incurvés (à retournement brusque ou cloquant) sont utilisés principalement comme interrupteurs thermiques. Les bilames entortillés en spirale ou hélicoïdaux offrent une plus grande sensibilité, ils sont alors plutôt utilisés comme thermomètres ou thermostats, figure 23.
Comme nous venons de le voir, les bilames peuvent être chauffés de plusieurs manières : par conduction (le bilame est directement en contact avec la source de chaleur), par convection ou par effet joule lors du passage d'un courant.
Figure 23. Bilame spiral utilisé comme thermomètre |
Il est simple et modique d'illustrer le fonctionnement d'un bilame. Par exemple, ici nous proposons de mettre en évidence le rôle d'interrupteur thermique d'un bilame à retournement brusque, figure 24.
Nous réalisons un circuit à l’aide d’une ampoule (témoin du passage du courant dans le circuit) en série avec un générateur et un thermostat bilame. Le bilame est initialement à température ambiante, il joue le rôle d’interrupteur ouvert, ce modèle est prévu pour se fermer dès que la température dépasse 60°C.
Une bougie, source chaude, est ajoutée pour faire monter la température du bilame. Dès que la température de basculement du bilame est atteinte, la courbure du bilame se renverse, le bilame se comporte comme un interrupteur fermé et l’ampoule s’allume. Si l’on fait refroidir le bilame, par exemple en le posant sur un sac de glaçons, jusqu’en dessous de sa température de consigne, la courbure se renverse et on retrouve un rôle d’interrupteur ouvert, la lampe s’éteint.
Ce bilame pourrait, par exemple, être employé pour activer une commande dès que la température d'une enceinte est supérieure à 60°C.
Source - © 2020 CultureSciences-Physique
Références
- [1] The measurmement, instrumentation and sensors handbook
- [2] Time Restored : The Story of the Harrison Timekeepers and R.T. Gould, "The Man who Knew (almost) Everything". Jonathan Betts, Senior Specialist, Horology, National Maritime Museum / Royal Observatory, Greenwich
- [3] John Harrison biography
- [4] SuisseMontre.com
- [5] Pratiques et techniques en plaisance, Les apports essentiels du XIXe siècle.
- [6] De quelle précision a-t-on réellement besoin en mer ?, Guy Boistel, Histoire et Mesure.
- [7] Comptes rendus des séances de l'académie des sciences, juillet-décembre 1865.
- [8] Catalogue Kanthal
- [9] Dilatation et contraintes thermiques dans les solides : application aux bilames, BUP n°940, janvier 2012.
- [10] Techniques de l'ingénieur
- [11] Traité de construction horlogère, Michel Vermot, Philippe Bovay, Damien Prongué. Presses polythechniques et universitaires romandes, 2011.
- [12] Applications des aciers au nickel à la chronométrie, Ch. Éd. Guillaume, 1904.
- [13] Thermostatic Bimetal Designer's Guide, Enginereed Materials Solutions.
Dossier : Physique et ingénierie des objets
Retrouvez les autres articles du dossier « Physique et ingénierie des objets ».
Retrouvez « Physique et ingénierie des objets » sur Culture Sciences de l'ingénieur.
Pour citer cet article :
Le bilame : principe de fonctionnement et applications, Delphine Chareyron, Hélène Horsin-Molinaro, novembre 2020. CultureSciences Physique - ISSN 2554-876X, https://culturesciencesphysique.ens-lyon.fr/ressource/bilame.xml