Activer le mode zen
Ressource au format PDF
Mots-clés
Classification
Champ magnétique et raies spectrales
22/09/2009
Résumé
Un article du dossier « La spectroscopie en astronomie ». Exemple de la détermination directe de la norme du champ magnétique moyen d'une étoile, basée sur l'effet Zeeman. Une brève description du phénomène physique de l'effet Zeeman est donnée en annexe.
Introduction
Dans les astres et leur environnement, la présence de champ magnétique est fréquente. D'importants phénomènes lui sont associés à des échelles très variées, depuis les taches et éruptions solaires jusqu'aux jets relativistes issus des quasars.
Les ordres de grandeur des champs magnétiques observés sont très différents d'un milieu à un autre, comme le montre le tableau suivant (champ B en Tesla).
107 - 1010 T | étoile à neutron ou pulsar |
106 - 10 T | étoile de type naine blanche |
10-2 - 1 T | étoile chaude magnétique |
0 - 10-4 T | planètes du système solaire (norme de 3 à 6.10-5 T à la surface terrestre) |
10-11- 10-9 T | nuage interstellaire |
La plupart des méthodes de mesure des champs magnétiques en astronomie sont basées sur l'effet Zeeman. L'influence d'un champ magnétique sur un atome modifie les propriétés des raies émises, ou absorbées, par l'atome qui est soumis au champ. Il s'applique aussi aux ions et molécules.
Une brève description du phénomène physique de l'effet Zeeman est donnée en annexe.
Grâce à l'effet Zeeman, la détection des champs magnétiques est possible à très grande distance, via le rayonnement reçu. Les applications astrophysiques sont nombreuses, plus ou moins directes et nécessitant parfois une modélisation théorique sophistiquée. Les méthodes diffèrent selon la nature des astres étudiés, la grandeur et la géométrie des champs magnétiques, les performances de l'observation en sensibilité et résolution spectrale.
On détecte aussi des variations du champ magnétique des étoiles au cours de leur rotation, ce qui donne des indices sur sa géomètrie globale. Les méthodes actuelles (technique de « spectropolarimètrie ») exploitent l'enregistrement supplémentaire de la polarisation circulaire en fonction de la longueur d'onde, ce qui permet de déterminer séparément les composantes du champ, parallèle ou perpendiculaire à la direction d'observation et de déduire des cartes de champ détaillées.
L'exemple proposé illustre un cas où le champ magnétique dans une étoile est assez intense et la résolution spectrale suffisante pour que l'on puisse séparer les raies individuelles de la figure Zeeman. La mesure des écarts entre les composantes Zeeman conduit alors à une détermination directe de la norme du champ magnétique moyen.
Observation d'une étoile fortement magnétique
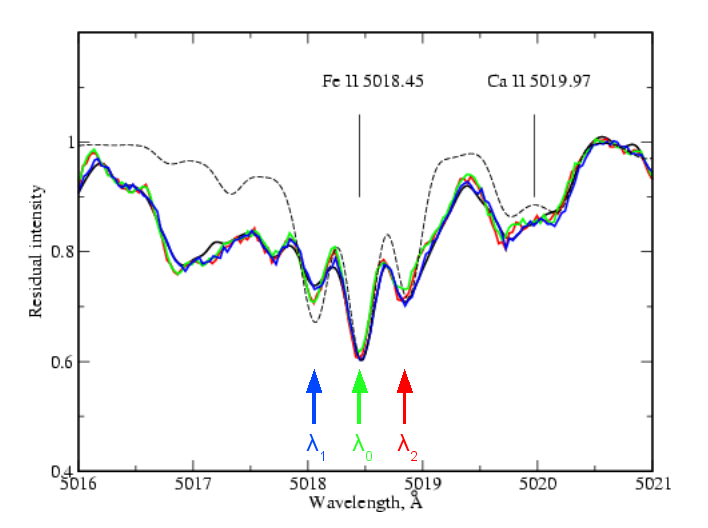
Certaines des étoiles de type A ou B (plus chaudes que le soleil, de température effective comprise entre 8000 et 20 000 K) comportent un champ magnétique dont la structure à grande échelle est globalement celle d'un dipôle. La figure 1 montre la mise en évidence directe d'un tel champ magnétique, particulièrement intense, grâce à l'enregistrement à haute résolution d'une raie d'absorption du fer ionisé.
Légende originale : The spectrum of HD 178892 in the vicinity of the Fe II 5018.45 Å line. Solid lines show high-resolution observations, whereas dashed line represents synthetic spectrum calculation with <Bs> = 17.5 kG.
Traduction : Spectre de l'étoile HD 178892 autour de la raie de Fe II à la longueur d'onde de 5018,45 Ångström (soit 501,845 nm). Les spectres en trait continu représentent des observation à haute résolution (40 000 environ). Le spectre synthétique en pointillé est calculé avec <Bs> = 17,5 kGauss (soit 1,75 Tesla)
Trois flèches ont été ajoutées pour pointer les trois raies de la figure Zeeman.
Source : HD 178892 - a cool Ap star with extremely strong magnetic field, Ryabchicova et al., Astronomy&Astrophysics 445, L47–L50 (2006)
Interprétation de la figure Zeeman de la raie de Fe II
La raie de Fe II absorbée par l'ion Fe+ à la longueur d'onde λ0 = 501,845 nm est répertoriée dans les banques de spectres atomiques qui en donnent les caractéristiques (voir par exemple http://physics.nist.gov/PhysRefData/ASD/index.html).
Les deux états quantiques, inférieur et supérieur, de la transition sont :
3d5 4s2 a6S | 3d6(5D)4p z6P0 | configurations électroniques en notation conventionnelle et couplage LS |
23317,633 | 43238,586 | énergies des niveaux en cm-1 |
2,5 | 2,5 | nombres quantiques J |
1,996 | 1,869 | facteur de Landé gL |
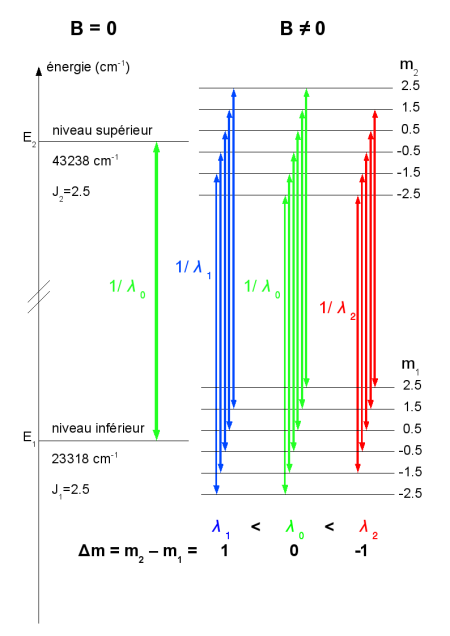
La figure Zeeman de cette raie comporte seulement trois composantes : on voit en effet que la transition de Fe II se compose d'une raie non déplacée λ0 = 5018,45 Å et de deux raies supplémentaires de longueurs λ1 = 5018,06 Å et λ2 = 5018,84 Å. Ceci s'explique parce que les niveaux initiaux et finaux de la transition ont la même valeur de J = 2,5 et des facteurs de Landé voisins gL ≈ 1.9 (les valeurs de gL varient entre 1 et 3 habituellement ). Le schéma ci-dessous représente les transitions permises.
Sur la figure 1, on peut estimer l'écart entre les raies décalées et la raie centrale à la valeur Δλ ≈ 0,39 Å = 0,039 nm. À partir de la relation 3 (cf. annexe) et en admettant l'approximation z ≈ gL ≈ 1.9 on obtient bien la valeur de B = 17,5 kGauss annoncée.
Remarquez que l'auteur note le champ <Bs> : en effet le champ magnétique n'est pas uniforme sur la surface de l'étoile et comme le spectre est enregistré avec le rayonnement provenant de tout le disque stellaire, c'est bien une moyenne de la valeur de B sur le disque stellaire qui est mesurée grâce à la raie de Fe II.
On peut également noter que la raie de Ca II apparaissant sur le spectre ne présente pas de figure Zeeman claire. La raison est que pour cette transition on prévoit z ≈ 1 car les facteurs de Landé des niveaux sont plus petits. La figure Zeeman plus étroite n'est pas résolue sur ce spectre.
Conclusion :
La description du champ magnétique des étoiles présente un grand intérêt pour la compréhension de leur structure et évolution. Elle permet de mieux comprendre et modéliser les mécanismes hydrodynamiques des atmosphères stellaires.
Les étoiles ayant un champ magnétique stable à grande échelle, comme celle de l'exemple précédent, ont la particularité de ne plus avoir de symétrie sphérique. L'axe du dipole magnétique est en général différent de l'axe de rotation propre de l'étoile et de la direction d'observation. Selon les orientations relatives de ces trois axes, le disque qui apparait au cours d'une rotation de l'étoile peut présenter successivement les zones polaires ou équatoriales de l'étoile. En répétant les observations sur plusieurs nuits, on enregistre des variations périodiques du rayonnement et du spectre. Celles-ci révèlent une structure inhomogène de la surface de l'étoile que l'on relie aux propriétés du champ magnétique.
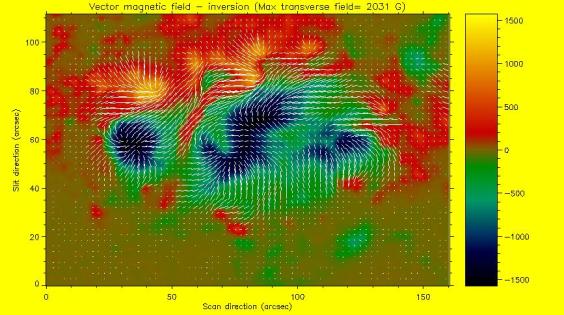
Les étoiles de type solaires, plus froides, ont une surface dominée par les mouvements convectifs. L'activité magnétique se manifeste alors par des champs et flux fluctuants à petite échelle. Ils sont bien décrits dans le cas du soleil : tâches, éruptions, flux coronaux... Pour les étoiles, les progrès actuels des observations reposent sur les méthodes de « spectropolarimètrie » qui combinent la spectrographie et la détection de la polarisation.
Image tirée de la banque solaire BASS2000. Elle montre l'ordre de grandeur des B locaux (kGauss) et le coté aléatoire qui suggère l'activité magnétohydrodynamique de l'atmosphère. La carte montre une portion du disque solaire (150 x100 arcsec) à comparer au diamètre 32 minute.
Source : Banque solaire BASS 2000, Cartes de champ magnétique vecteur en ligne
Annexe : physique de l'effet Zeeman
L'effet Zeeman est dû à la levée de dégénérescence d'un niveau d'énergie en présence d'un champ magnétique. Un état quantique d'un atome, ion ou molécule, est caractérisé par des nombres quantiques entiers ou demi-entiers. Notamment deux nombres quantiques définissent le moment cinétique total J (entier ou demi-entier) des électrons de la particule : ce sont J pour son module et m pour sa projection sur un axe Oz quelconque, m prenant les valeurs -J, -J+1,..., J-1, J.
En l'absence de champ l'espace est isotrope, la direction Oz est arbitraire et l'énergie peut dépendre de J, mais pas de m.
Quand il existe un champ B, supposé orienté selon Oz, celui-ci interagit avec le moment magnétique M associé au moment cinétique J, selon l'image classique de la précession du dipôle magnétique autour du champ magnétique, le dipôle étant dû à la structure du cortège électronique de l'atome.
Il en résulte la levée de dégénérescence des niveaux d'énergies : les énergies E correspondant aux états m sont décalées proportionnellement à la valeur du champ B, selon la formule :
E(m) = E(0) + μB gL m B (équation 1)
μB est le magnéton de Bohr qui dépend des constantes fondamentales μB = eh/4πme, μB = 9,27.10-24 J T-1. gL est le facteur de Landé, un nombre généralement compris entre 1 et 3 qui caractérise la relation entre le moment cinétique et le moment magnétique pour l'état atomique considéré.
En spectroscopie, les énergies E des niveaux et des transitions (hν = E2 - E1) sont couramment exprimées en cm-1, unité correspondant au nombre d'onde σ = 1/λ. Le facteur de conversion est : σ (en cm-1) = σ (en m-1)/100 = 0,01 x E (en J) / hc = E (en J) x 0,503.1023. On obtient numériquement, E étant exprimé en nombre d'onde en cm-1 et B en Tesla : E(m) = E(0) + 0,467 gL m B (équation 2).
Une raie spectrale due aux transitions entre deux niveaux d'énergie E1 et E2, de nombres quantiques J1, J2, est alors décomposée en plusieurs raies distinctes, les composantes Zeeman, selon les nombres quantiques m1 et m2, compte tenu de la règle de sélection Δm = m2 - m1 = 0 ou ±1.
Dans le spectre du rayonnement émis ou absorbé, on observe une « figure Zeeman » composée de raies individuelles de différentes intensités et polarisations (linéaire, circulaire gauche ou circulaire droite). Elle est symétrique autour de la raie observée en champ nul, car chaque valeur de m a son opposé -m.
Les caractéristiques des figures Zeeman des atomes et ions sont déterminées à partir des calculs quantiques de structure électronique et parfois observées en spectroscopie de laboratoire.
L'écart entre une composante Zeeman de longueur d'onde λ et la raie non déplacée à λ0 se déduit du déplacement des niveaux d'énergie. Au lieu du facteur de Landé gL, il intervient un coefficient z, qui combine les facteurs gL des deux niveaux de la transition Zeeman selon les intensités des raies individuelles se superposant à la longueur d'onde λ.
Avec les unités utilisées sur la figure, longueurs d'onde en Ångström et champ magnétique en kGauss, on obtient numériquement : λ - λ0 = 4,67 10-10 λ02 z B (équation 3).
Retour au sommaire du dossier « La spectroscopie en astronomie ».
Pour citer cet article :
Champ magnétique et raies spectrales, Marie-Christine Artru, septembre 2009. CultureSciences Physique - ISSN 2554-876X, https://culturesciencesphysique.ens-lyon.fr/ressource/Spectre-champ-magnetique-etoiles.xml