Température effective

La température effective d'une étoile est directement reliée à la puissance totale qu'elle rayonne. C'est par définition la température d'un corps noir dont la surface émettrait la même puissance par unité de surface que l'étoile. Il s'agit ici de la puissance bolométrique, c'est-à-dire incluant l'ensemble du rayonnement électromagnétique, des rayons X au ondes radio.

Connaissant la température effective T_eff et le rayon R d’une étoile, on évalue la puissance totale émise (luminosité) L = 4 π R² σ T_eff⁴, où σ est la constante de la loi de Stefan relative à l’émittance d'un corps noir de température T_eff.

L'avantage de cette définition est de fournir une bonne approximation de la température de surface de l'étoile. En effet la forme globale d'un spectre stellaire est assez voisine de celle d'un corps noir, car son rayonnement provient essentiellement d'une émission thermique assez superficielle pour que la plupart des photons émis émergent de l’atmosphère stellaire.

Par exemple, la température effective du soleil est de 5770 K. Son spectre tracé ci-dessous se compare assez bien à celui du corps noir à cette température (courbe rouge). Notons aussi que le maximum de puissance spectrale apparaît dans le jaune, à une longueur d'onde voisine de 500 nm, ce qui est conforme à la loi de Wien λ(μm) = 2898 / T(K).

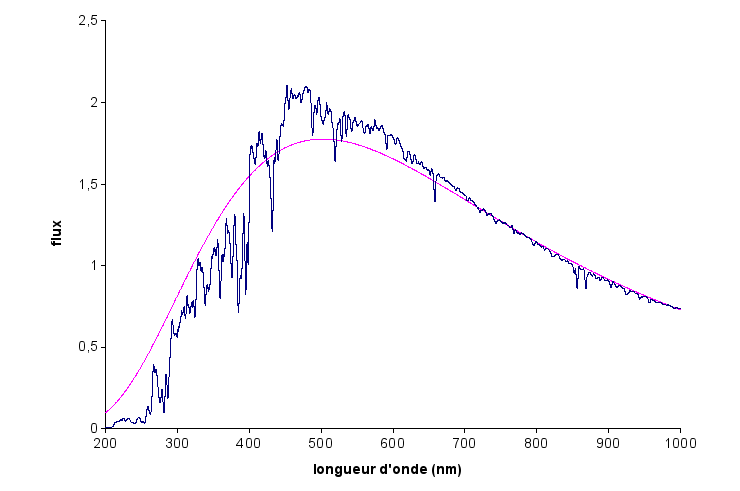
Pour ce graphe, l'unité de flux est W.m^-2.nm^-1 ce qui correspond à l'éclairement (par unité d'intervalle spectral en nm) reçu en un point proche de la Terre, hors de l'atmosphère.