Mettre en évidence les deuxième et troisième lois de Kepler à l'aide de codes en langage python

Sur le portail d'éphémérides de l'IMCCE [6], on ouvre la page « Éphémérides de position », figure 2.

Figure 2.  Portail des formulaires de calcul d'éphémérides Source : IMCCE

On sélectionne un corps du Système solaire : par exemple Mercure, Mars, ou encore la comète périodique 2P/Encke qui possède une période de quelques années adaptée à cet exercice.

On choisit la date initiale, le nombre de dates à calculer et le pas temporel. Ces paramètres sont importants pour la suite et doivent être adaptés à la période de l'astre choisi. Pour Mars : 1 calcul par jour pendant 700 jours permet d'avoir une précision correcte, car une année martienne dure environ 686,98 jours solaires. Pour Mercure, on pourra prendre un incrément de 1 heure seulement, et environ 90 jours (une année sur Mercure dure environ 87,97 jours).

Pour les autres champs à renseigner, on choisit :

Après avoir cliqué sur « Calculer », on obtient un tableau des positions de l'astre, que l'on peut exporter dans un fichier au format .csv (comma separated values). On renomme ce fichier du nom de l'astre choisi pour l'enregistrer dans le dossier où se trouvera le script Python. Ce fichier comporte une ligne par date calculée, et plusieurs paramètres en colonnes, dont les coordonnées cartésiennes de la position de l'astre.

Nous proposons ici, de mettre à disposition les fichiers contenants les données astronomiques de Mercure (mercure.csv [résolution de une heure, durée de 89 jours à partir du 1er janvier 2025]), Mars (mars.csv [résolution de un jour, durée de 700 jours à partir du 1er janvier 2025]), et de la comète Encke (comete_2PEncke.csv [résolution de 6 heures, durée de 3,3 ans à partir du 1er janvier 2025]) pour lesquels les calculs et illustrations sont présentés dans la suite de l'article.

On importe les bibliothèques python nécessaires au traitement des données et à l'affichage des graphiques. Nous importons ici les données du fichier .csv avec la bibliothèque « pandas ».

On importe les données du fichier .csv (coordonnées de la planète Mercure) :

Figure 3. Aperçu de la variable « astre » (un tableau de type DataFrame), contenant les éphémérides de Mercure à partir du 1er janvier 2025 pour 700 jours avec un pas de temps de 1 heure La première colonne allant de 0 à 2150 est l'index du tableau ; c'est un moyen d'accéder facilement à une ligne donnée.

Pour calculer l'aire balayée par l'astre sur un temps donné, nous disposons, à l'aide du fichier des éphémérides, des positions successives de l'astre dans le temps. Pour Mercure, nous avons choisi un pas d'échantillonnage d'une heure sur sa période de révolution (un peu moins de 88 jours). L'astre passe ainsi de sa position décrite en coordonnées cartésiennes par le point (x_n, y_n, z_n) au temps t_n au point (x_n+1, y_n+1, z_n+1) au temps t_n+1 en une heure.

À l'aide du calcul de l'angle \( d\theta \) entre deux positions successives \( n \) et \( n+1 \), on peut remonter à une approximation de la longueur \( dL \) de l'arc de l'orbite balayée. On assimile la portion d'arc à celle d'un cercle de rayon \( r_n \). La longueur de la portion d'arc s'écrit alors \( dL = d\theta \times r_n\). Une telle approximation n'est raisonnable que si la variation entre les deux instants est très faible devant la période du mouvement.

Figure 4. Schéma de principe de mesure de l'aire en utilisant la position et l'angle de l'astre Source : Delphine Chareyron.

Ainsi la portion d'aire \(dA\) balayée pendant la durée \(dt\) peut être assimilée à \( dA_n = \frac{1}{2} r^2_n \times d\theta\), à chaque pas de temps.

Pour le calcul des aires balayées autour des points choisis (aphélie, périhélie, point quelconque), on définit une période temporelle (pour Mercure 120 h) centrée sur chaque point (60 h avant et 60 h après).

Revenons au code, il faut maintenant définir plusieurs fonctions (calcul de l'angle \( d\theta \) et calcul de l'aire), ainsi que les coordonnées du périhélie et de l'aphélie.

Notons ici que nous choisissons de travailler dans le plan de l'écliptique, ainsi, on n'utilisera pas la composante z de l'astre. Cet argument est légitime pour les astres tels que Mercure et Mars dont le plan de l'orbite dévie très peu de l'axe de l'écliptique.

Remarque : avec matplotlib, les angles du graphe polaire sont en radians, mais les graduations sont affichées en degrés.

On calcule les coordonnées polaires avec une commande du module pandas. On utilise les fonctions correspondantes au tableau (dataframe) ‘astre', et on stocke les résultats dans des nouvelles colonnes du même tableau :

On utilise ‘df' pour travailler dans la dataframe et le nom de la variable temporaire pour le tableau de données.

On prépare l'affichage de la figure :

On trace la trajectoire :

Pour le calcul de l'aire autour d'un point quelconque, le code tire au hasard une valeur d'index dans le tableau 'astre' contenant les coordonnées au cours du temps. La variable 'signe' sert à ce que le point aléatoire soit tantôt d'un côté tantôt de l'autre de l'ellipse, mais ce n'est pas indispensable. Le tirage est fait de sorte que l'aire de ce troisième point ne se superpose pas aux deux autres.

On calcule les aires balayées autour du périhélie (indice 1), de l'aphélie (indice 2) et d'un point quelconque de l'orbite (indice 3) :

On affiche les aires calculées sur la figure :

Remarque : le texte est affiché en coordonnées de la fenêtre graphique entre 0 et 1.

On finit la mise en page de la figure et on l'enregistre.

Figure 5.  Mesure des aires sur une durée de 120 heures autour du périhélie, de l'aphélie et d'un point quelconque de la trajectoire de la planète Mercure Source : David Alberto et Delphine Chareyron.

Remarques : On observe que l'on a une bonne concordance des aires calculées, avec une différence à 10^-6 UA² pour les aires au périhélie et à l'aphélie. Comme on pouvait s'y attendre, l'aire calculée autour du périhélie est plus grande. En effet, la longueur d'arc assimilée à un cercle surestime la longueur d'arc de l'ellipse.

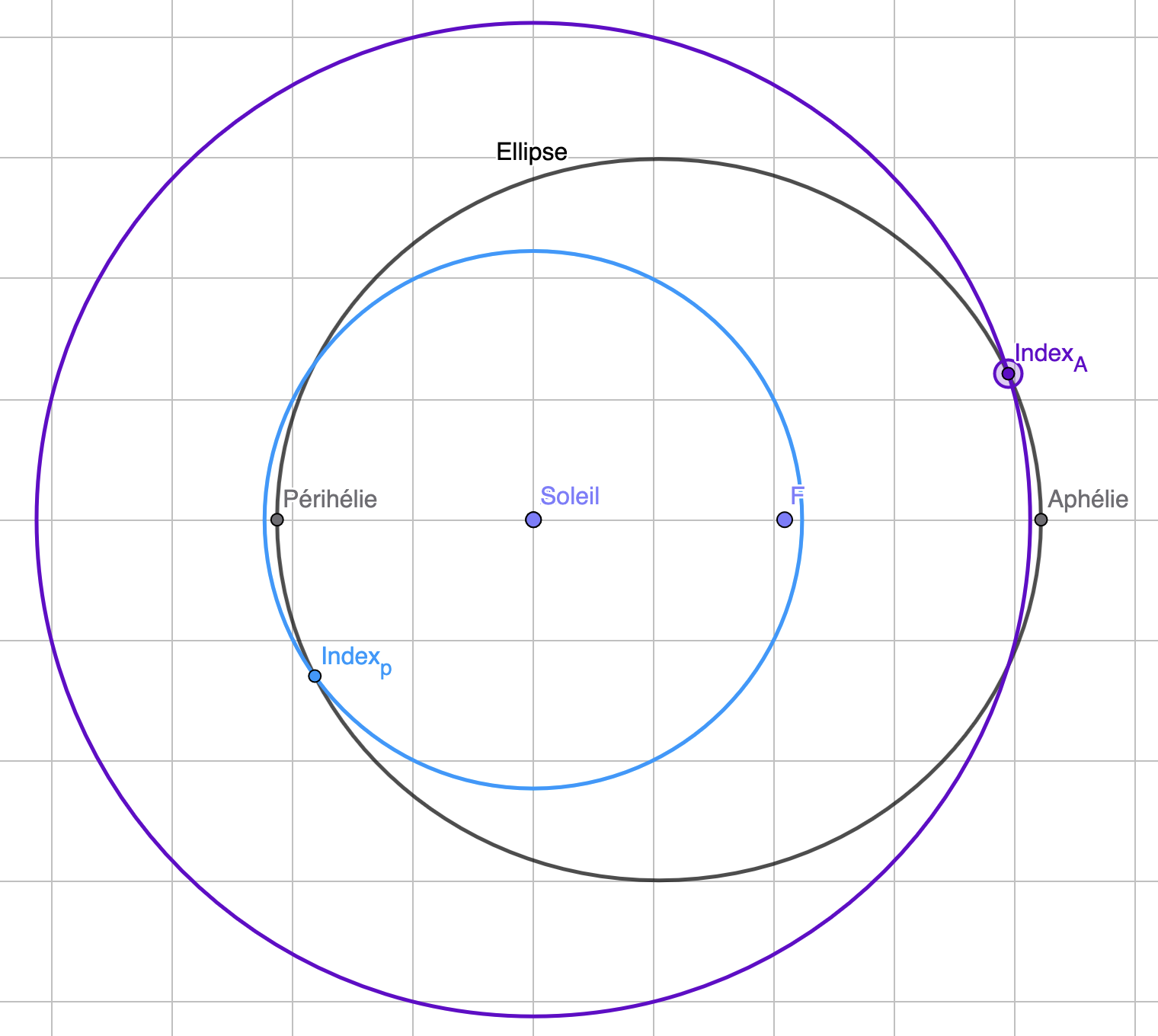
On a mis en évidence, de manière très schématique, cet effet sur la figure 6. En noir, nous avons représenté une orbite elliptique de foyers : le Soleil et le point F. Nous avons annoté le périhélie et l'aphélie. En bleu nous avons tracé un cercle de centre le Soleil et de rayon la distance Soleil-Index_p (représentant par exemple le point à partir duquel on va calculer l'aire aurour du périhélie). En violet, nous avons tracé un cercle de centre le Soleil et de rayon la distance Soleil-Index_A (même chose, autour de l'aphélie).

Figure 6.  Représentation de l'orbite elliptique d'un astre en noir dont les foyers sont le Soleil et le point F. Le cercle bleu est centré sur le Soleil et a pour rayon Soleil-Index_p. Le cercle violet est centré sur le Soleil et a pour rayon Soleil-Index_A Source : Delphine Chareyron, Geogebra.

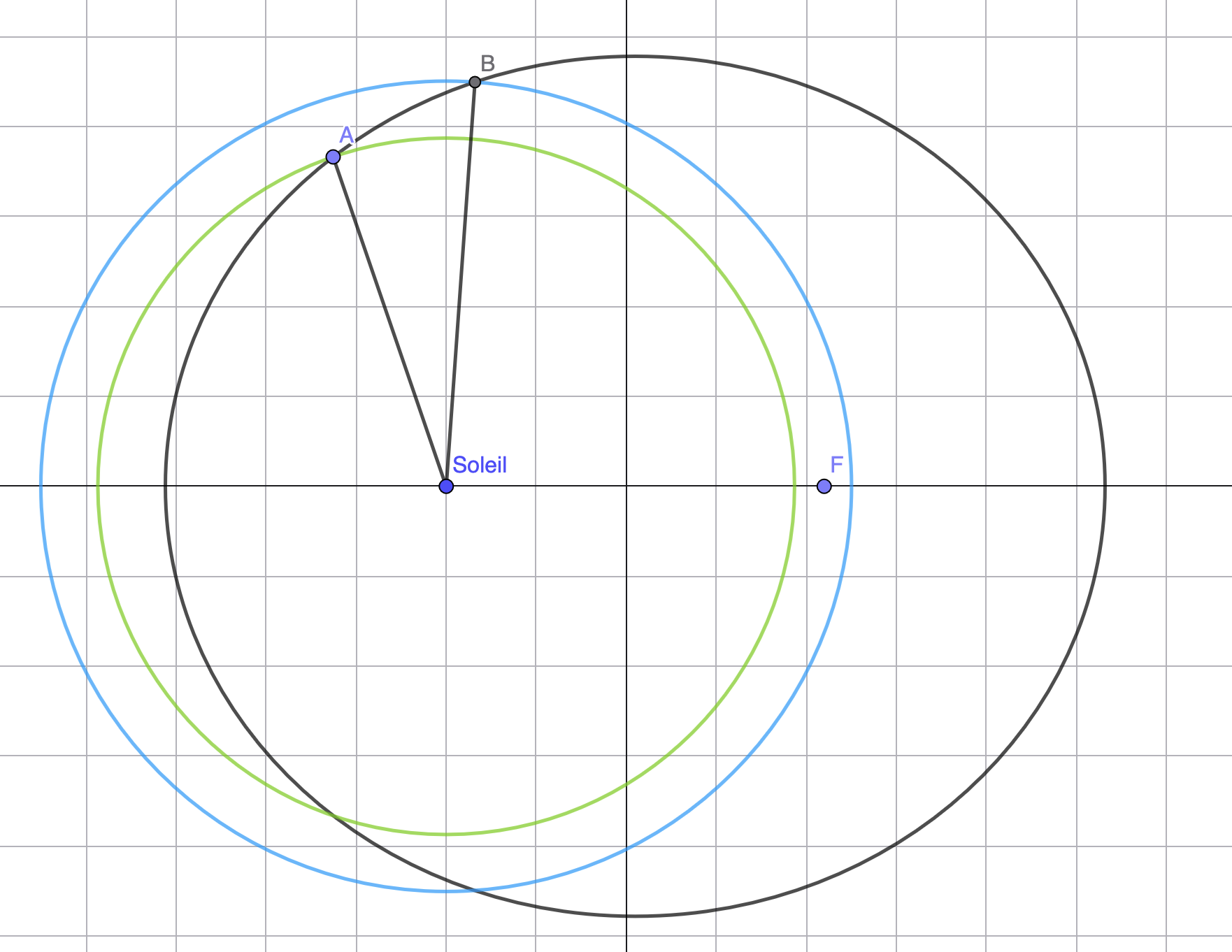
Pour l'aire calculée autour d'un point quelconque de la trajectoire, on trouve une valeur beaucoup plus grande, figure 5. En effet, on se rend compte qu'en fonction du point de l'orbite, l'approximation de la longueur d'arc d'ellipse par un arc de cercle va soit sous-estimer soit surestimer la portion d'ellipse, figure 7.

Figure 7. Représentation de l'orbite elliptique d'un astre en noir dont les foyers sont le Soleil et le point F. Le cercle vert est centré sur le Soleil et a pour rayon Soleil-A. Le cercle bleu est centré sur le Soleil et a pour rayon Soleil-B. Source : Delphine Chareyron, Geogebra.

La figure 8 présente la trajectoire et le calcul des aires balayées pour la planète Mars sur une durée de 40 jours autour du périhélie, de l'aphélie et d'un point quelconque. Le pas de résolution est de 1 jour. Comme l'excentricité de l'orbite est assez faible, on a une bonne concordance des trois mesures d'aires.

Figure 8. Mesure des aires sur une durée de 40 jours autour du périhélie, de l'aphélie et d'un point quelconque de l'orbite pour la planète Mars Source : David Alberto et Delphine Chareyron

La figure 9 présente la trajectoire et le calcul des aires balayées pour la planète comète PEncke sur une durée de 4 jours autour du périhélie, de l'aphélie et d'un point quelconque. Le pas de résolution est de 6 heures. Si l'on augmente la durée de l'aire balayée avec ce pas de résolution, on devine que l'approximation de l'aire dans la zone du périhélie sera beaucoup plus entachée d'erreur.

Figure 9. Mesure des aires sur une durée de 4 jours autour du périhélie, de l'aphélie et d'un point quelconque de l'orbite pour la comète 2P-Encke Source : David Alberto et Delphine Chareyron

Avec cette approximation de la mesure d'arc d'ellipse balayé, on observe que l'on va toujours surestimer ou sous-estimer l'aire en fonction d'où on se place sur l'orbite, figure 7. On pourrait ainsi raffiner la méthode en faisant une moyenne sur le vecteur position \(r\), en prenant par exemple \(r= \frac{1}{2} (r_n+r_{n+1})\)

Pour le calcul de l'aire, on peut aussi utiliser la vitesse de l'astre sur le long de son orbite. À l'aide des positions de l'astre sur la trajectoire, il est facile de remonter au vecteur vitesse pour chaque pas de temps.

Dans le code, dans la définition de la fonction de calcul d'aire, il suffit de rajouter une ligne pour calculer le vecteur vitesse (vit) en coordonnées cartésiennes :

Les vecteurs r1 et r2 sont deux tuples \((x,y,z)\). Pour soustraire membre à membre ces deux tuples, on utilise la fonction map(fonction lambda, tuples) qui permet d'appliquer ici la fonction lambda (anonyme, que l'on définit) à chaque élément des tuples (comme une itération). La fonction lambda définie ici correspond à la soustraction membre à membre de ces deux tuples (index \(i\) du tuple r2 moins index \(j\) du tuple r1). On obtient ainsi une vitesse \((v_x,v_y,v_z)\), pour Mercure en U.A./h puisque le pas d'échantillonnage est de 1 heure.

Il faut ensuite prêter attention aux angles entre le vecteur position de l'astre et son vecteur vitesse. En effet, on ne peut pas simplement choisir de faire le produit de la norme des deux vecteurs. Nous représentons très schématiquement sur la figure 10 deux cas représentatifs.

À l'aphélie (ou au périhélie), le vecteur vitesse est quasiment perpendiculaire au vecteur position, ainsi, réaliser le calcul de l'aire en l'assimilant à sa norme \( dA = \frac{1}{2} \times \lVert \vec{v_m} \rVert \times \lVert \vec{r_m} \rVert \times dt \) est une approximation correcte.

Par contre, pour d'autres points de la trajectoire, cette approximation n'est plus du tout justifiable, car elle va surestimer ou sous-estimer la portion d'aire \(dA\) à prendre en compte.

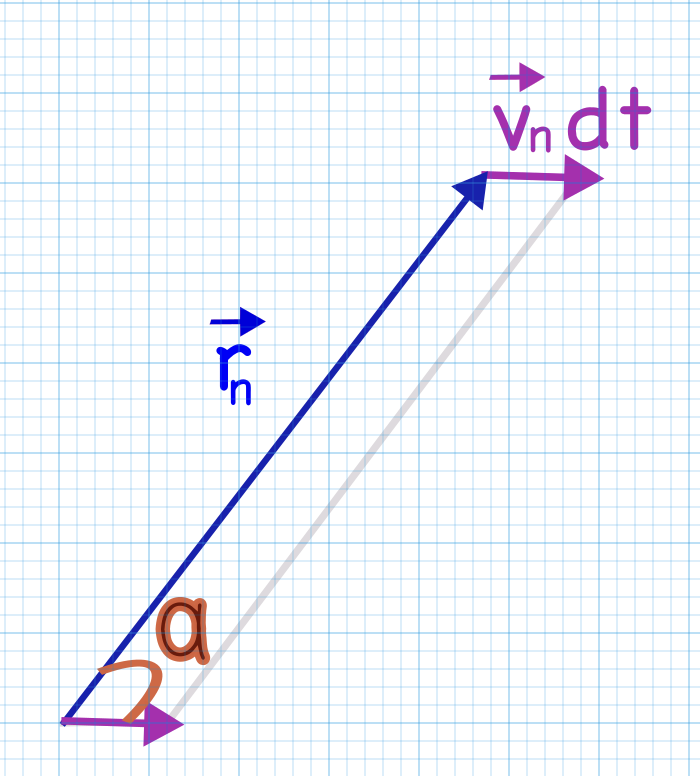
Il est alors nécessaire de calculer l'angle alpha entre le vecteur vitesse et le vecteur position afin de pouvoir calculer l'aire correspondant à la moitié du parallélogramme, figure 11.

On a alors \( dA = \frac{1}{2} \times \lVert \vec{v_n} \rVert \times \lVert \vec{r_n} \rVert \times dt \times \sin(\alpha)\)

Figure 10. Représentation très schématique des vecteurs vitesses en deux point (aphélie et point quelconque) de la trajectoire Source : Delphine Chareyron

Figure 11. \( \alpha \) est l'angle entre le vecteur position et le vecteur vitesse Source : Delphine Chareyron

La fonction définissant le calcul de l'aire dans le code est alors :

Pour le calcul de l'aire, nous utilisons la fonction np.linalg.norm() intégrée dans la bibliothèque d'algèbre linéaire de numpy. Cette fonction permet de calculer la norme d'un vecteur.

Nous obtenons, pour le même pas de temps (1 h) et la même durée que précédemment (120 h), pour la planète Mercure, des aires proche à 10^-6 UA² près, figure 12.

Figure 12. Mesure des aires sur une durée de 120 heures autour du périhélie, de l'aphélie et d'un point quelconque de l'orbite pour la planète Mercure. Calul de l'aire en utilisant le vecteur vitesse et le vecteur position Source : David Alberto et Delphine Chareyron

De la même manière, on calcule les aires balayées avec les mêmes durées pour Mars et pour la comète PEncke, figures 13 et 14.

Figure 13. Mesure des aires sur une durée de 40 jours autour du périhélie, de l'aphélie et d'un point quelconque de l'orbite pour la planète Mars. Calul de l'aire en utilisant le vecteur vitesse et le vecteur position Source : David Alberto et Delphine Chareyron

Figure 14. Mesure des aires sur une durée de 4 jours autour du périhélie, de l'aphélie et d'un point quelconque de l'orbite pour la comète PEncke. Calul de l'aire en utilisant le vecteur vitesse et le vecteur position Source : David Alberto et Delphine Chareyron

Sur une orbite très elliptique, telle que celle de la comète, le calcul de l'aire balayée basé sur les vecteurs position et vitesse est beaucoup plus robuste que celui présenté avec l'approximation de la longueur de l'arc de cercle (section 2.2). En effet, on peut largement augmenter la durée de l'aire balayée, par exemple à 20 jours, figure 12, on obtient encore des valeurs très proches à 10^-4 UA².

Figure 15. Mesure des aires sur une durée de 20 jours autour du périhélie, de l'aphélie et d'un point quelconque de l'orbite pour la comète PEncke. Calul de l'aire en utilisant le vecteur vitesse et le vecteur position Source : David Alberto et Delphine Chareyron

Remarque : pour les calculs présentés ici, on aurait pu directement utiliser le produit vectoriel. Ici le détail avec le calcul de l'angle est donné comme un guide pédagogique et dépendant de l'avancement en connaissances mathématiques des élèves.

L'aire du parallélogramme, (figure 11, est directement la norme du produit vectoriel entre le vecteur vitesse \( v \)dt et le vecteur position \(r\). Ainsi, dans le code en python, cela revient à écrire la portion d'aire : dA = 1/2 * np.linalg.norm(np.cross(vit,r1))

Finalement, pour le calcul de l'aire, on aurait aussi pu utiliser la formule de Heron.