Activer le mode zen
Ressource au format PDF
Mots-clés
Classification
Les saisons sur Terre, répartition de l'énergie solaire et paramètres orbitaux
07/02/2022
Résumé
Obliquité et répartition hémisphérique de l'énergie. Solstices, équinoxes et saisons.
Table des matières
- 1. Une orbite elliptique
- 2. Une planète sphérique en rotation sur elle-même, effet de latitude
- 3. Une obliquité non nulle à l'origine des variations saisonnières avec opposition Nord/Sud
- 4. L'effet de la rotation sur les redistributions énergétiques latitudinales
- 5. Récapitulatif – Le pourquoi des saisons
- 6. Calculs simples et compléments
- Références
Un poster pour accompagner l'article
Un poster reprend les points-clés de l'article. Il est basé sur les figures originales conçues par les auteurs mais dessinées par un illustrateur pour un rendu plus esthétique. Ces figures, plus ou moins complétées selon les besoins, sont aussi reprises dans l'article. Un graphiste a composé le poster avec des contraintes assez fortes. En effet, outre son rendu équilibré et fluide devant permettre au plus grand nombre de se plonger dans le contenu scientifique, il est possible de l'imprimer en plusieurs tailles, du A4 au A1, selon les moyens à disposition.
Le poster Les saisons sur Terre est disponible en version “proche d'un A1” (4,3 Mo), mais peut aussi convenir pour plus petit (A4, A3, A2) et la définition permet même d'envisager une impression à un format proche d'un A0.
Chacun, par exemple en Europe, sait que l'hiver il fait plus froid, les jours sont courts et le Soleil reste bas sur l'horizon alors que l'été il fait plus chaud, les jours sont longs et le Soleil est haut sur l'horizon. De plus, même sans avoir voyagé au loin, on sait (télévision, internet…) que les saisons sont inversées entre les hémisphères Nord et Sud, ce qui est, par exemple, marqué par le fait que les grands opens de tennis ont lieu en juin-juillet au Nord (Roland-Garros en France, Wimbledon en Angleterre) et en janvier au Sud (Melbourne en Australie). Pourtant, quand on demande à un étudiant scientifique de niveau bac+2, voire à un étudiant de niveau bac+4 ou 5 préparant les concours de l'enseignement secondaire, d'expliquer la succession des saisons sur Terre on obtient rarement d'emblée la bonne réponse. Des explications basées sur la latitude et l'angle d'incidence des rayons solaires sont souvent proposées pour rendre compte de la zonation climatique latitudinale au premier ordre (climats équatorial, tropical, tempéré, polaire). Bien sûr, d'autres aspects sont vite invoqués (proximité à l'océan, direction des vents dominants, altitude, chaines de montagne…) pour expliquer les variantes de second ordre (aride / humide, océanique / continental, montagnard…) voire les particularités locales (adret / ubac). En insistant pour avoir une explication satisfaisante de la cyclicité annuelle des saisons (été/hiver) avec opposition Nord-Sud (été au Nord pendant l'hiver au Sud), l'ellipticité de l'orbite terrestre est malheureusement alors trop souvent donnée comme argument, puis le déclic se fait quelques fois en sortant un globe terrestre et une lampe (pour mimer le Soleil)… mais pas toujours.
Nous allons ici revoir quels sont les paramètres expliquant la succession des saisons sur Terre (2 ou 4 saisons marquées par des variations de température – saison chaude / froide et/ou d'humidité – saison sèche / humide) avec opposition entre les deux hémisphères.
1. Une orbite elliptique
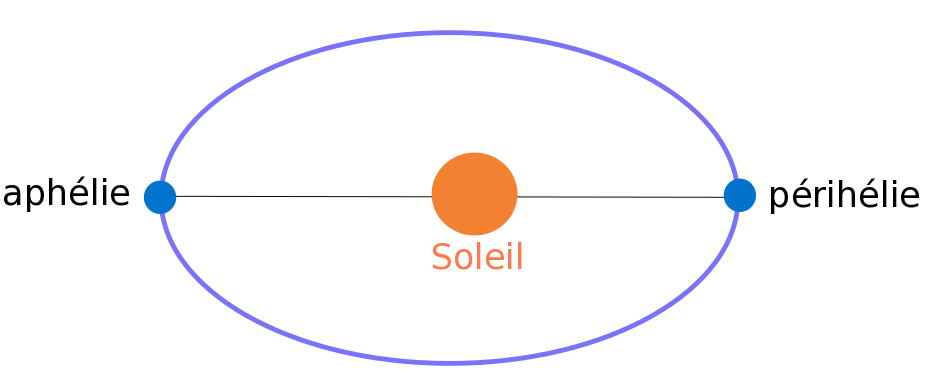
Depuis le début du XVIIe siècle et les travaux de Kepler, on sait que la Terre tourne autour du Soleil en décrivant, non pas un cercle centré sur le Soleil, mais une ellipse dont le Soleil occupe l'un des foyers.
La distance Terre-Soleil est donc variable au cours de l'année. Actuellement, la distance moyenne est d'environ 149,6 Gm [1 Gm = 1 milliard de mètres ou 1 million de kilomètres], aux environs du 4 janvier cette distance est minimale (périhélie) et de l'ordre de 147,1 Gm, alors que 6 mois plus tard, aux environs du 4 juillet, elle est maximale (aphélie) et de l'ordre de 152,1 Gm.
Figure 1. Représentation “exagérée” de la trajectoire elliptique de la Terre autour du Soleil Au périhélie, la distance est minimale et est d'environ 147,1 Gm, et à l'aphélie, la distance est maximale et de l'ordre de 152,1 Gm [1 Gm = 1 milliard de mètres ou 1 million de kilomètres]. |
On peut calculer la différence d'énergie reçue par la Terre entre sa position la plus proche et la plus éloignée, et même estimer les différences maximales de température induites. Ainsi (voir 6. Calculs simples et compléments), pour une puissance pm moyenne, on a une puissance réduite à l'aphélie pa = 0,967 pm et une puissance augmentée au périhélie pp = 1,034 pm, ce qui, pour une température moyenne de 15°C, donne des températures extrêmes d'équilibre à l'aphélie Ta ≈ 12,6°C et au périhélie Tp ≈ 17,4°C.
On aurait donc une saison chaude, une saison fraiche et deux saisons intermédiaires… mais cela concerne la Terre entière, hémisphères Nord et Sud en même temps, donc cela ne peut expliquer l'opposition Nord/Sud observée ! En effet, la Terre est au périhélie (maximum d'énergie) vers le 4 janvier et à l'aphélie 6 mois plus tard vers le 4 juillet, ce qui correspond bien à l'été en janvier et à l'hiver en juillet au Chili, en Australie ou en Afrique du Sud… mais pas dans l'hémisphère Nord (hiver au périhélie et été à l'aphélie). De plus l'écart de température estimé (de l'ordre de 5°C) est bien inférieur à ce que l'on peut communément observer entre été et hiver par exemple en France métropolitaine.
⇒ La variation de distance Terre-Soleil au cours de la trajectoire elliptique de la Terre autour du Soleil n'est donc pas la cause de l'existence des saisons terrestres marquées avec opposition Nord/Sud.
2. Une planète sphérique en rotation sur elle-même, effet de latitude
La Terre est en révolution autour du Soleil, mais aussi en rotation sur elle-même autour d'un axe de rotation qui permet de définir :
- les pôles (points où l'axe de rotation “perce” la surface),
- l'équateur (grand cercle perpendiculaire à l'axe de rotation).
À partir de ces éléments, on mesure la latitude, angle entre le plan de l'équateur et la droite reliant le centre de la planète au point étudié de la surface, qui varie de 0° à l'équateur à 90° aux pôles.
2.1 Planète sphérique en rotation sur elle-même
Prenons le cas simple d'une planète dont l'axe de rotation est perpendiculaire au plan de l'écliptique, plan sur lequel se dessine l'orbite de révolution autour du Soleil. L'angle entre l'axe de rotation et la perpendiculaire au plan de l'écliptique définit l'obliquité. Dans le cas présent, l'obliquité est nulle (figure 2) (ce qui est quasiment le cas de Mercure et Jupiter).
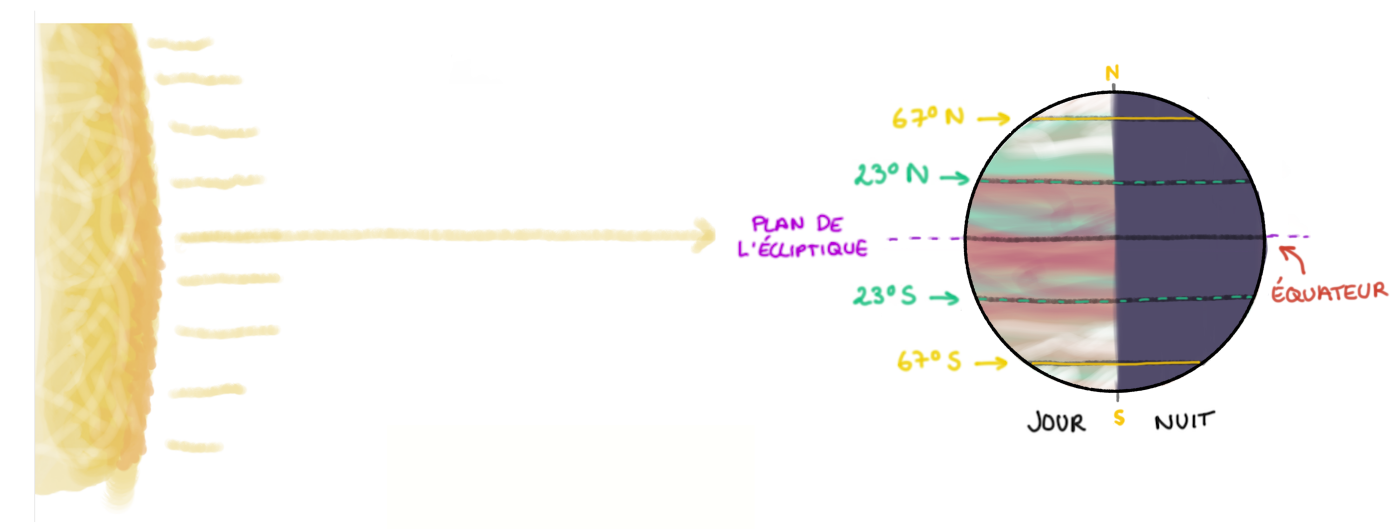
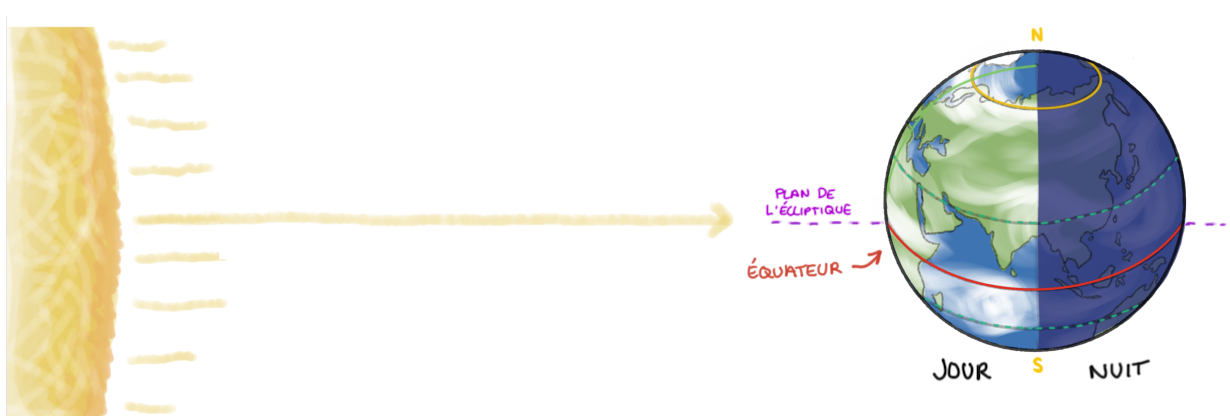
Sur la figure 2, cette planète d'obliquité nulle est vue “de côté”, depuis le plan de l'écliptique, horizontale de référence. Elle tourne autour du Soleil en s'éloignant de l'observateur et, en nommant “Nord” le haut de la figure, elle tourne sur elle-même d'Ouest en Est (ici, de gauche à droite, dans le “sens inverse des aiguilles d'une montre”). L'axe de rotation, perpendiculaire au plan de l'écliptique, est contenu dans le plan formé par la limite jour (partie éclairée, à gauche) / nuit (partie non éclairée à droite), plan par définition perpendiculaire au rayonnement solaire. Le plan de l'équateur est dans le plan de l'écliptique. Sont représentés l'équateur (en rouge) et les parallèles Nord et Sud de latitudes 23° (en tiretés verts) et 67° (en jaune).
Du fait de la taille du Soleil par rapport à celle de la planète (taille du Soleil fortement minimisée pour le dessin) et de son éloignement, les “rayons du Soleil” atteignant la planète sont tous parallèles entre eux et parallèles à l'axe centre du Soleil - centre de la planète. |
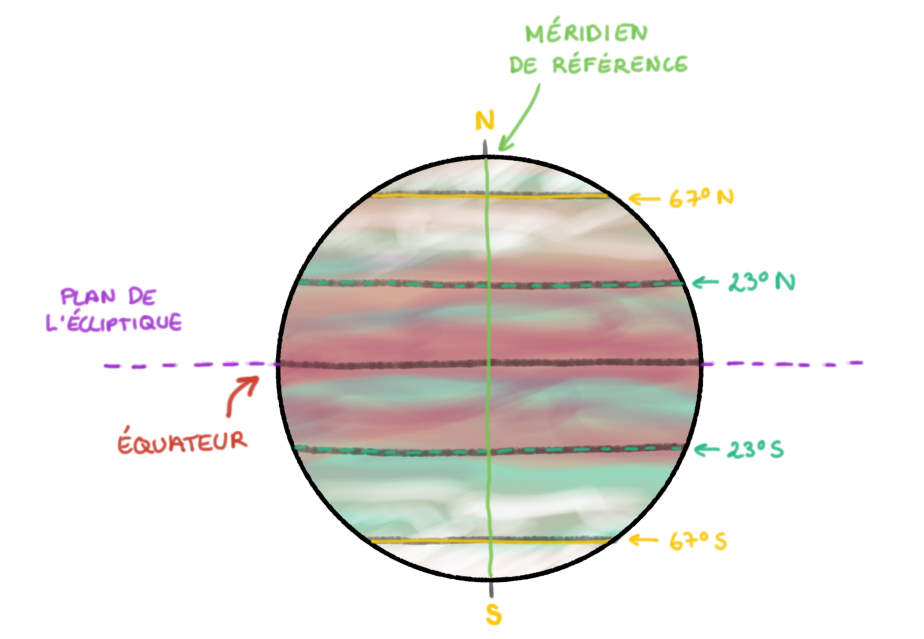
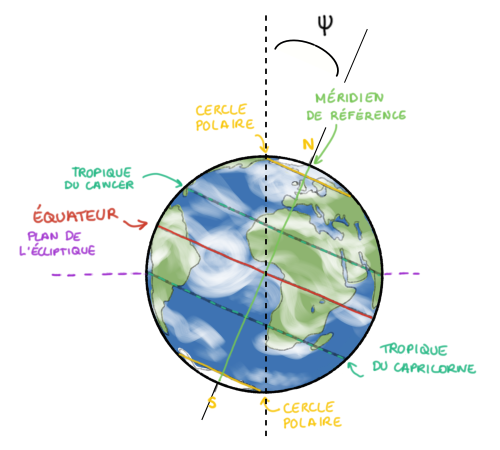
Sur la figure 3, on observe la face éclairée de la planète. Cette vue “de face” est celle que l'on obtient en étant sur le plan de l'écliptique avec le Soleil dans le dos (on voit la planète telle que vue depuis le Soleil), le plan de l'écliptique comme horizontale de référence et le Nord en haut. L'équateur sépare le disque planétaire éclairé en deux demi-disques de même surface. Les deux hémisphères, Nord “au-dessus” du plan de l'écliptique et Sud “au-dessous” du plan de l'écliptique, reçoivent la même quantité d'énergie solaire.
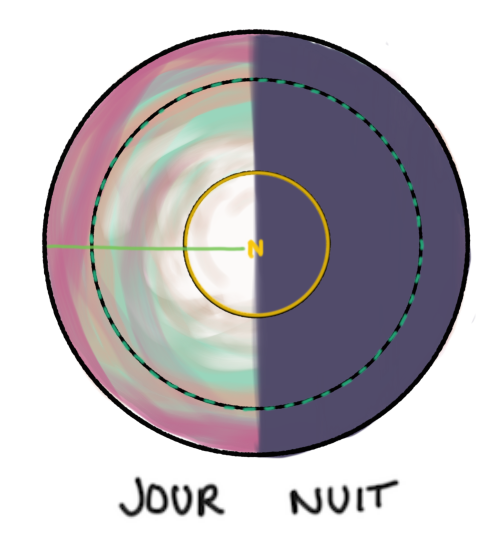
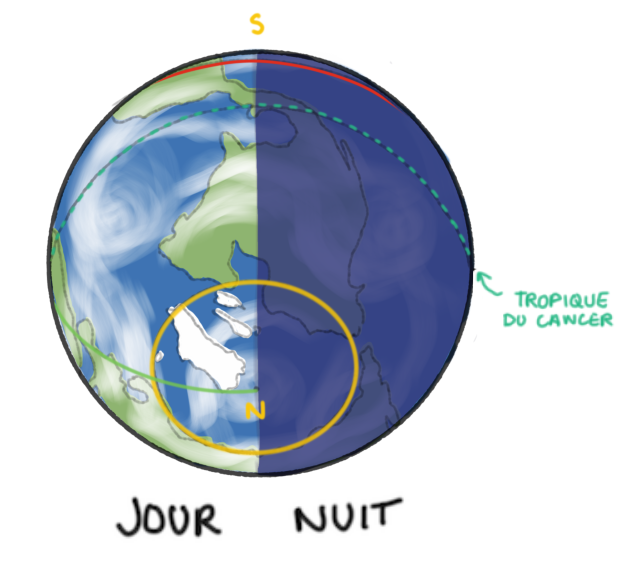
Sur la figure 4, on observe la planète depuis le “dessus”, c'est-à-dire depuis un point situé au Nord du plan de l'écliptique, à la “verticale” de la planète (en prenant l'écliptique comme horizontale de référence). Au cours d'une rotation, un point décrit un cercle de latitude donnée et on observe que la moitié de son trajet est “éclairé” et l'autre moitié “non éclairé”. En d'autres termes, en tout point de la planète, le jour dure autant que la nuit.
Sur les figures précédentes, est aussi représenté en vert un méridien de référence passant par les pôles, moitié d'un grand cercle perpendiculaire au plan de l'équateur. Il est positionné à “midi”, position obtenue lorsque le plan du grand cercle contient l'axe Soleil-planète et que le méridien fait “face” au Soleil.
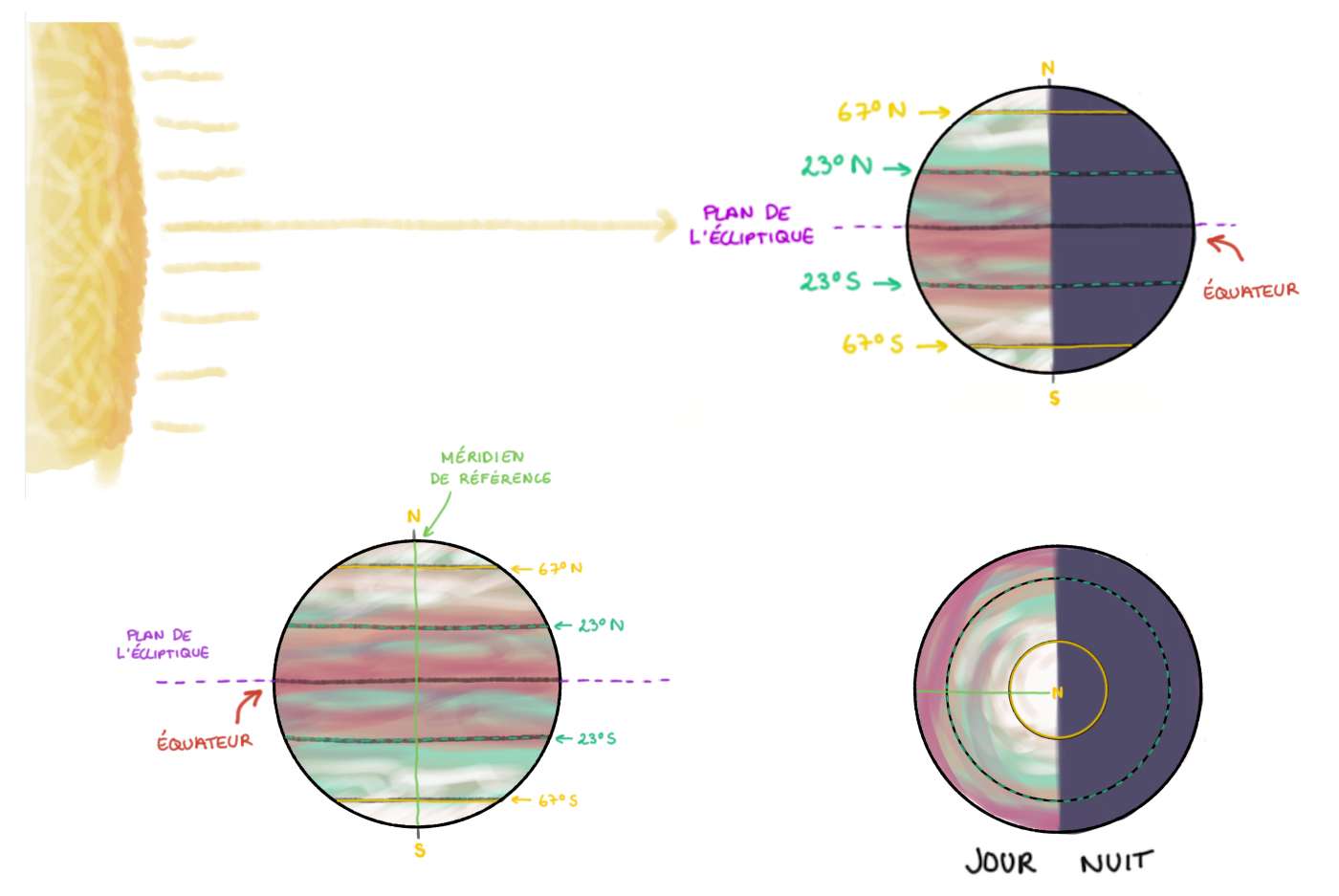
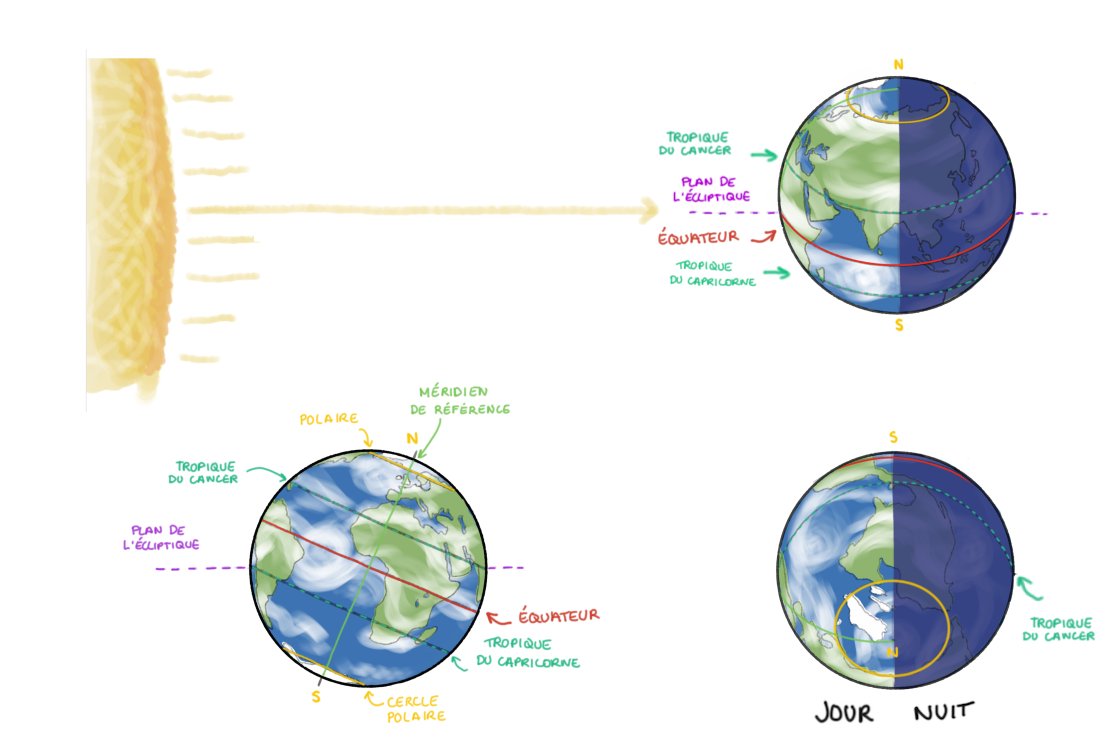
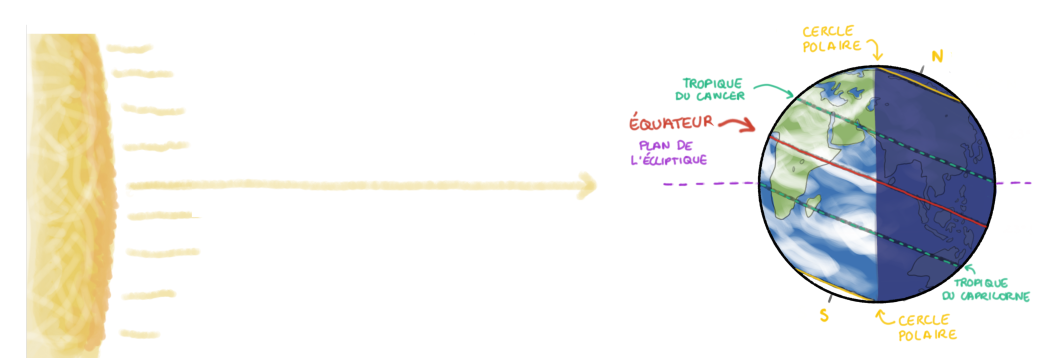
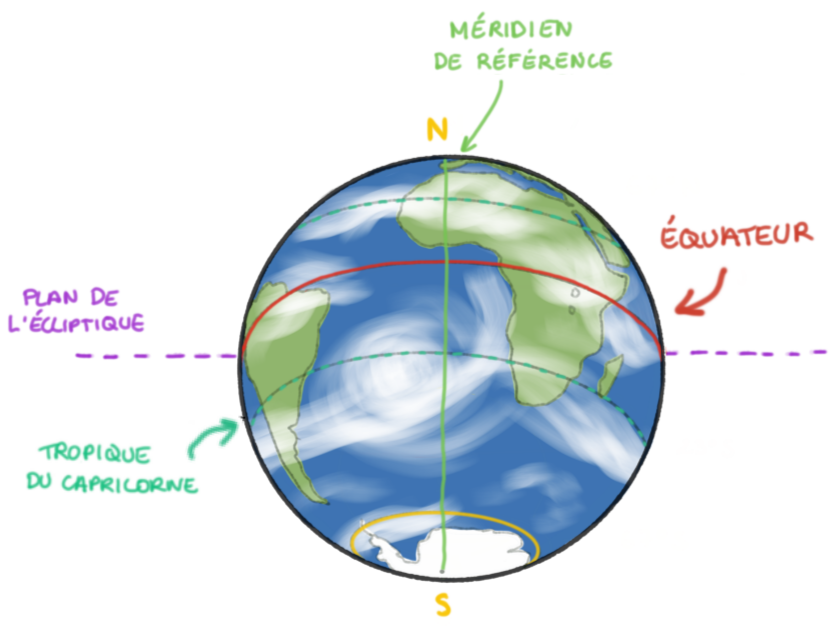
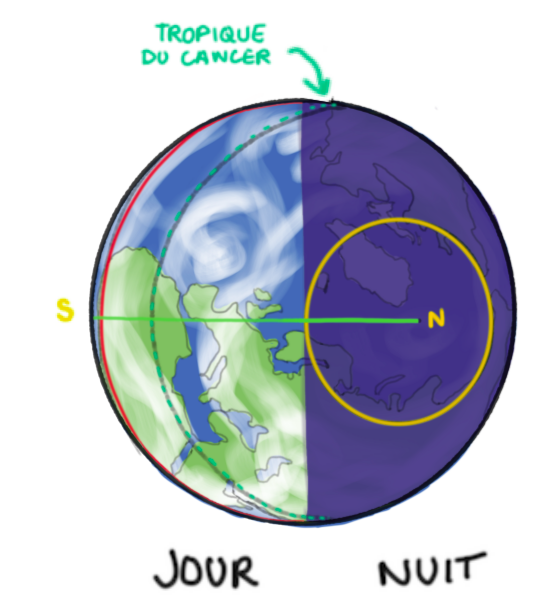
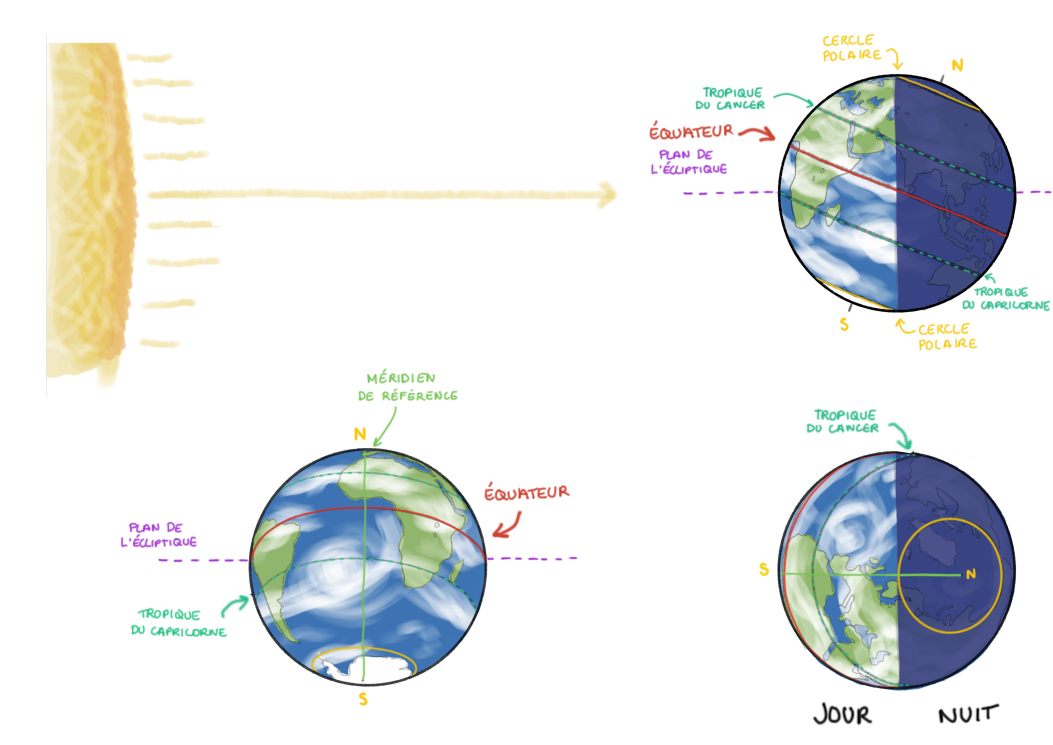
La figure 5 est une illustration synthétique de ces trois vues, “de côté”, de “face” et “de dessus”.
Haut : vue “de côté” ; bas gauche : vue “de face” ; bas droite : vue “de dessus”. |
2.2 Effet de la latitude
Si la variation de distance au Soleil entre périhélie et aphélie a un impact certain sur la puissance solaire reçue par la Terre à un moment donné de sa révolution, certains tentent d'expliquer les variations d'énergie reçue par la Terre par sa distance au Soleil. Est alors invoquée la différence de distance entre le point du disque éclairé le plus proche du Soleil et les points les plus éloignés situés à la limite jour/nuit. Sur la figure 3 cela correspond à la différence entre le point de l'équateur situé à “midi” (au centre de la face éclairée) et, par exemple, le pôle Nord. On montre très rapidement (voir 6. Calculs simples et compléments) que cette différence de distance est si faible que la différence relative de puissance solaire résultante n'est que de 85.10−6 (85 millionièmes).
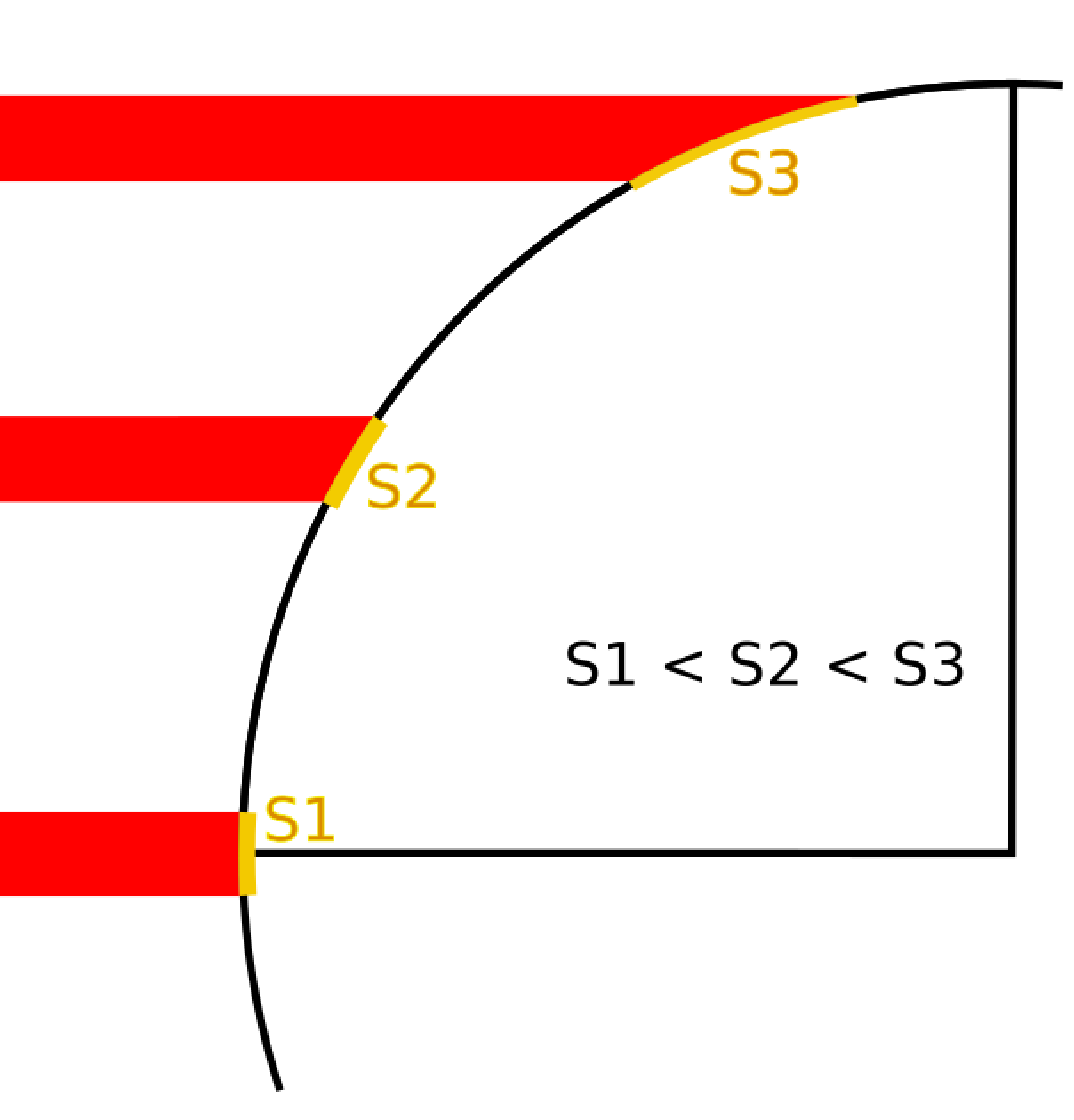
Par contre, si la rotondité de la Terre n'induit pas de variation notable de puissance solaire liée à la distance au Soleil, elle induit une variation de la puissance solaire reçue au sol en fonction de la latitude. La figure 6 permet de comprendre cela : pour un faisceau solaire de section (donc de puissance) donnée, plus on monte en latitude plus la surface éclairée augmente, donc la puissance par unité de surface diminue. Ainsi, une même énergie est répartie sur une surface plus grande au sol aux pôles qu'à l'équateur.
Figure 6. Puissance solaire reçue au sol en fonction de la latitude Pour un faisceau solaire de puissance donnée, la surface au sol “éclairée” à midi augmente avec la latitude. À l'équateur le rayonnement solaire est perpendiculaire au sol, cet angle (angle d'incidence) diminue en montant en latitude. Aux pôles, le rayonnement est rasant. |
On peut raisonner à puissance solaire fixe (figure 6). Plaçons nous sur le méridien de référence “face au Soleil” ; pour une puissance solaire donnée (un faisceau solaire de section donnée), la surface au sol éclairée augmente lorsqu'on monte en latitude : la puissance reçue au sol par unité de surface diminue donc.
On peut aussi raisonner à surface au sol fixe (surface horizontale), voir 6. Calculs simples et compléments, pour retrouver le même résultat. On voit alors (tableau 1) par exemple que la puissance reçue au sol diminue de 8% à 23° de latitude et de 60% à 67°.
En considérant que la température est le principal facteur climatique, la variation latitudinale de puissance solaire reçue au sol explique la répartition latitudinale des zones climatiques du plus chaud à l'équateur vers le plus froid vers les pôles. Mais si la rotondité de la Terre explique cette zonation climatique, on n'a pour l'instant toujours pas de différence entre les hémisphères Nord et Sud (jours de 12h partout et énergie répartie de manière symétrique de part et d'autre de l'équateur). On a donc une zonation climatique mais toujours pas d'opposition Nord/Sud dans les saisons.
⇒ Une planète dont l'axe de rotation est perpendiculaire au plan de l'écliptique ne connait pas l'existence de saisons avec opposition Nord/Sud.
3. Une obliquité non nulle à l'origine des variations saisonnières avec opposition Nord/Sud
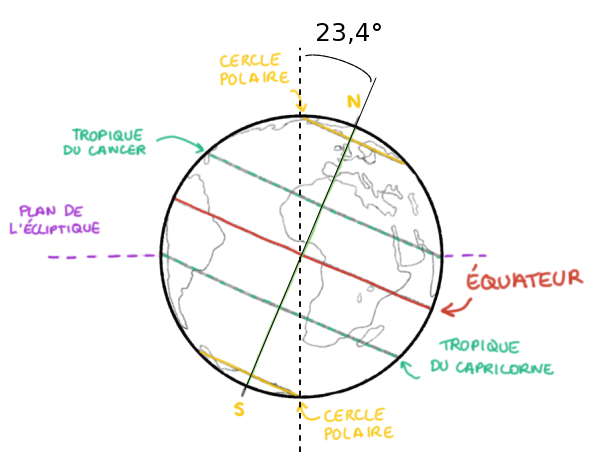
L'axe de rotation de la Terre n'est pas perpendiculaire au plan de l'écliptique mais il est incliné d'environ ψ=23,4° par rapport à cette perpendiculaire (figure 7).
Les tropiques sont les parallèles de latitude ψ : les cercles polaires ceux de latitude 90°−ψ. |
3.1 Révolution autour du Soleil de la Terre et d'une planète d'obliquité nulle
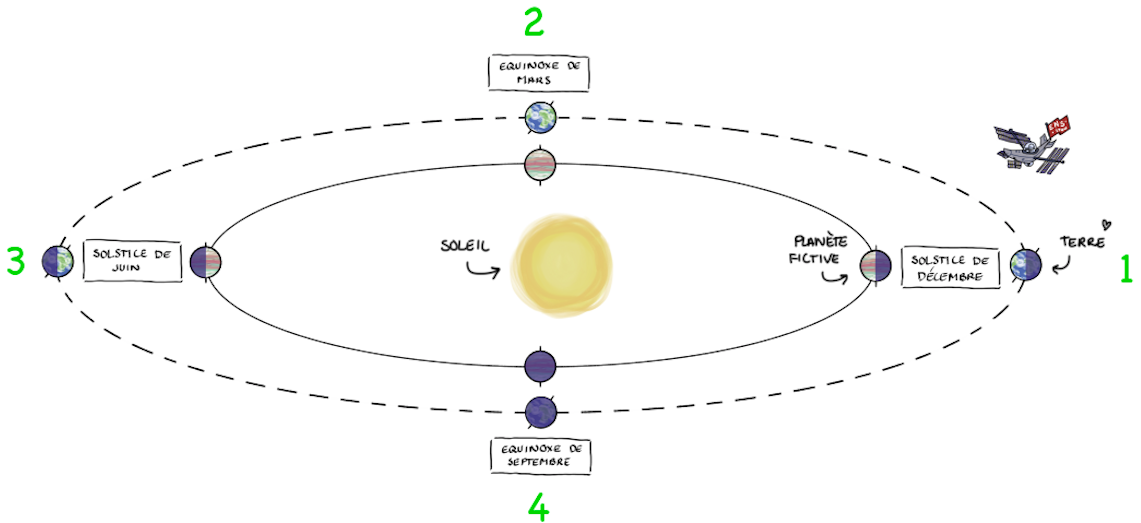
Conséquence directe de cette obliquité, l'angle entre le plan équatorial terrestre et le plan de l'écliptique est lui aussi égal à ψ. Du fait de cette obliquité, la Terre ne se présente pas toujours de la même façon face au Soleil au cours d'une révolution annuelle (figure 8). Au cours de l'année, 4 positions particulières sont atteintes, deux situations “équilibrées” d'équinoxe (positions 2 et 4 sur la figure 8) et deux positions “extrêmes” de solstice (positions 1 et 3 sur la figure 8).
Figure 8. Révolution terrestre et positions des équinoxes et des solstices L'obliquité de la Terre induit 4 positions particulières : 2 solstices (positions 1 et 3) et 2 équinoxes (positions 2 et 4). Aux équinoxes, l'axe de rotation est dans le plan jour/nuit et est donc perpendiculaire à l'axe Soleil-Terre. Aux solstices, l'axe de rotation “pointe vers le Soleil” (sa projection sur le plan de l'écliptique est confondue avec l'axe Soleil-Terre). De l'une de ces positions à la suivante, l'axe de rotation vu du Soleil semble avoir fait un quart de tour. |
L'exposition de la Terre aux équinoxes et solstices induit des répartitions d'énergie particulières pour les deux hémisphères (énergie également répartie aux équinoxes et contraste maximal d'énergie aux solstices).
Par rapport au cas d'une planète d'obliquité nulle, les positions d'équinoxe et de solstice sont décrites dans les figures ci-dessous. Les tropiques (latitude ψ) et les cercles polaires (latitude 90°−ψ) sont des repères utiles.
3.2 Équinoxe de mars
Les figures 9, 10, 11 et 12 décrivent l'équinoxe de mars (position 2 sur la figure 8).
La figure 9 représente une vue “de côté”. L'axe de rotation est contenu dans le plan formé par la limite jour/nuit et est donc perpendiculaire au rayonnement solaire (axe Soleil-Terre). Dans cette position, le plan de l'équateur est sécant au plan de l'écliptique selon l'axe Soleil-Terre. Le point d'incidence maximale est sur l'équateur.
Figure 9. Équinoxe de mars (printemps au Nord, automne au Sud) - Vue “de côté” Du fait de la taille du Soleil par rapport à celle de la Terre et de son éloignement, les “rayons du Soleil” atteignant la Terre sont tous parallèles entre eux et parallèles à l'axe Soleil-Terre. |
La figure 10 présente une vue “de face” de la Terre. Comme pour le cas d'une planète sans obliquité (figure 3), l'équateur est un diamètre de la face éclairée : les deux hémisphères, Nord et Sud, reçoivent donc la même quantité d'énergie solaire. Cette vue de face est l'équivalente de la vue sans obliquité mais tournée de ψ vers la droite. Le point d'incidence maximale / puissance maximale reçue au sol à midi, au centre de la face éclairée, est sur l'équateur. On peut voir exactement la moitié de chaque parallèle, jour et nuit ont des durées égales.
Sur cette vue de face, on remarque que les cercles de latitude terrestre donnée ont une latitude écliptique (angle obtenu en remplaçant le plan équatorial, utilisé pour la latitude terrestre, par le plan de l'écliptique) variable au cours de la journée (de gauche à droite) et peuvent même traverser ce plan. Certains parallèles particuliers sont alors définis. Les tropiques, de latitude terrestre ψ, sont des cercles limites. Entre tropique et pôle d'un hémisphère, les parallèles restent toujours du même côté de l'écliptique au cours de la journée. Par contre, pour les latitudes intertropicales, les parallèles traversent l'écliptique. Cercle particulier, l'équateur est toujours pour moitié de chaque côté de l'écliptique. À l'équinoxe, le centre de la face éclairée (point de puissance reçue au sol maximale) est sur l'équateur. Les cercles polaires, de latitude 90−ψ, correspondent aux cercles qui, sur la face éclairée, passent par les extrémités du diamètre perpendiculaire à l'écliptique, extrémités correspondant à l'axe d'obliquité nulle.
La figure 11 présente la vue “de dessus”, la limite jour/nuit sépare en deux moitiés égales tout cercle de latitude donnée : quelle que soit la latitude, le jour dure autant que la nuit ou, autrement dit, la nuit a la même durée – 12h – à toute latitude (équi- égale + nuit -noxe). On voit ici aussi que tout point de latitude au-delà du tropique du Cancer (Nord) reste toute la journée du côté Nord de l'écliptique. Le cercle polaire, moitié dans le jour et moitié dans la nuit, passe par le centre de cette vue qui correspond à la trace de l'axe perpendiculaire à l'écliptique passant par le centre de la Terre.
La figure 12 est une illustration synthétique de ces trois vues correspondant à l'équinoxe de mars.
Figure 12. Équinoxe de mars (printemps au Nord, automne au Sud) Haut : vue “de côté” ; bas gauche : vue “de face” ; bas droite : vue “de dessus”. |
3.3 Solstice de décembre
Les figures 13, 14, 15 et 16 décrivent le solstice de décembre (position 1 sur la figure 8).
La figure 13 représente une vue “de côté”. L'axe de rotation est basculé de ψ perpendiculairement à l'axe Soleil-Terre, le pôle Nord côté nuit et le pôle Sud côté jour. Dans cette position, c'est sur le tropique du Capricorne (Sud) que se trouve le point d'incidence maximale. Les cercles polaires tangentent la limite jour/nuit en restant dans la nuit pour le cercle polaire Nord, dans le jour pour le cercle polaire Sud. De manière générale, sur un parallèle donné, le jour est plus court que la nuit dans l'hémisphère Nord, alors que le jour est plus long que la nuit dans l'hémisphère Sud.
Figure 13. Solstice de décembre (hiver au Nord, été au Sud) - Vue “de côté” Du fait de la taille du Soleil par rapport à celle de la Terre et de son éloignement, les “rayons du Soleil” atteignant la Terre sont tous parallèles entre eux et parallèles à l'axe Soleil-Terre. |
La figure 14 présente une vue “de face”. Lors d'un solstice, c'est sur un tropique que se trouve le centre de la face éclairée, point d'incidence maximale / puissance maximale reçue au sol à midi. Ici c'est sur le tropique du Capricorne (Sud), on parle alors de solstice d'été dans l'hémisphère Sud (et de solstice d'hiver au Nord). L'équateur, sécant au plan de l'écliptique à gauche et à droite de la vue, est “décalé” vers le Nord. L'hémisphère Nord reçoit donc moins d'énergie que l'hémisphère Sud (aux solstices, on atteint la différence maximale avec environ 70 % de l'énergie pour l'hémisphère en été contre 30 % pour l'hémisphère en hiver – voir plus bas 6. Calculs simples et compléments).
Une vue de “dessus” est proposée sur la figure 15. Le cercle polaire Nord, entièrement dans la nuit, passe par le centre de cette vue qui correspond à la trace de l'axe de rotation pour une obliquité nulle (axe perpendiculaire à l'écliptique passant par le centre de la Terre). Le tropique du Cancer (Nord) est le parallèle de plus basse latitude entièrement visible.
La figure 16 synthétise les 3 vues correspondant au solstice de décembre.
Figure 16. Solstice de décembre (hiver au Nord, été au Sud) Haut : vue “de côté” ; bas gauche : vue “de face” ; bas droite : vue “de dessus”. |
3.4 Des saisons contrastées avec opposition Nord/Sud
Du fait de l'obliquité, la latitude terrestre d'un lieu (“hauteur” par rapport au plan de l'équateur) ne correspond que rarement à la latitude écliptique de ce lieu (“hauteur” par rapport au plan de l'écliptique). Ainsi, le point d'incidence maximale, surface au sol perpendiculaire au Soleil, est à 0° de latitude écliptique, mais la latitude terrestre correspondante varie entre 0° aux équinoxes (mars et septembre) et ψ aux solstices (de latitude Nord en juin, de latitude Sud en décembre).
Cela induit, sauf aux équinoxes, une différence de puissance solaire totale reçue par chaque hémisphère (contraste maximal 70 % / 30 % aux solstices), avec durée variable du jour et de la nuit (jours plus longs que les nuits dans l'hémisphère qui reçoit le plus d'énergie). Aux alentours des équinoxes (vers les 21 mars et 21 septembre) on a donc des saisons avec répartition d'énergie “équilibrée”. De l'équinoxe de mars à l'équinoxe de septembre, l'hémisphère Nord reçoit plus d'énergie que l'hémisphère Sud et les jours y sont plus longs que les nuits. C'est l'inverse pour la période allant de l'équinoxe de septembre à l'équinoxe de mars.
Deux points de même latitude mais chacun dans un hémisphère ont, sauf aux équinoxes, des différences d'énergie perçue et des jours de durée différente (jour plus long que la nuit pour le point du côté de l'été). On a donc toujours une opposition de saison Nord/Sud à latitude égale.
⇒ C'est l'obliquité non nulle de l'axe de rotation de la Terre qui induit l'existence de saisons contrastées avec opposition Nord/Sud.
On a ici rattaché les régions intertropicales à l'hémisphère correspondant alors que ces régions passent du Nord au Sud de l'écliptique au cours de la journée, même si chaque région reste rattachée à son hémisphère terrestre en ce qui concerne la saisonnalité comme on va l'expliquer ci-dessous. En effet, au solstice de décembre, le tropique Sud est au Nord de l'écliptique mais est en été alors que l'hémisphère terrestre Nord est en hiver.
4. L'effet de la rotation sur les redistributions énergétiques latitudinales
L'énergie perçue par un point de latitude donnée dépend, on l'a vu, de sa latitude et de la date en fonction desquelles la puissance solaire maximale à midi et la durée du jour varient.
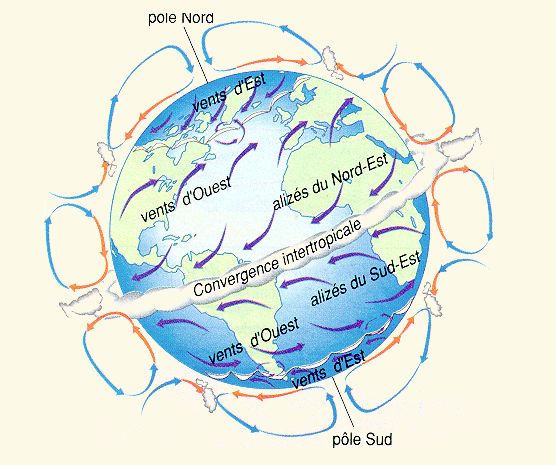
Le Soleil chauffe le sol qui, lui, réchauffe alors l'atmosphère. L'air chaud ayant tendance à monter, il se crée des mouvements chauds ascendants. Si de l'air monte à un endroit, il y a nécessairement de l'air qui descend ailleurs, et des mouvements latéraux entre les deux : des cellules de convection se forment. Ces cellules atmosphériques redistribuent l'énergie des zones d'air ascendant vers les zones descendantes, figure 17.
Comme le sol est plus ou moins chauffé partout, le facteur dominant est la montée de l'air chaud : c'est là où l'ascendance thermique est maximale que l'on a une branche ascendante, donc entre les tropiques. On s'attend donc à une branche ascendante tropicale avec des vents des basses vers les hautes latitudes en altitude allant alimenter une branche descendante polaire (là où le sol est le moins chaud) et des vents au sol des hautes vers les basses latitudes qui ferment la boucle (figure 17).
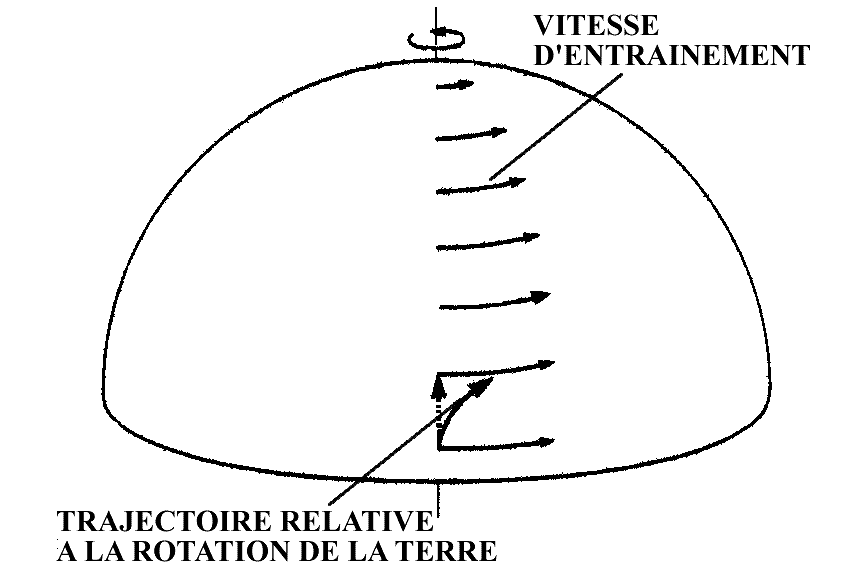
Mais à cela s'ajoute la rotation de la Terre sur elle-même et l'effet Coriolis qui en découle (figure 18, on pourra consulter, par exemple, « Modéliser l'effet Coriolis ? », « La mystérieuse force de Coriolis »).
Figure 17. Cellules de convection dans l'atmosphère Source : webedu, Eduscol | Figure 18. Mise en évidence de l'effet Coriolis Source : Planet-Terre |
Le premier impact est que cet effet Coriolis sépare les masses d'air de part et d'autre de l'équateur : masses détournées vers la droite dans l'hémisphère Nord et vers la gauche dans l'hémisphère Sud (figures 17 et 18). L'énergie thermique reçue au sol et redistribuée par les mouvements atmosphériques reste donc cantonnée dans son hémisphère d'origine.
Deuxième impact, la vitesse de rotation de la Terre induit une telle déviation latérale des vents de direction Nord-Sud que ceux-ci sont “rabattus” sur un parallèle bien avant d'arriver en zone polaire (figure 17). La branche descendante de la cellule équatoriale n'atteint donc pas les pôles. De plus, une branche ascendante ne pouvant s'exprimer aux pôles, on a toujours une branche ascendante équatoriale et une branche descendante polaire. Si la cellule équatoriale s'arrête avant les pôles, alors une cellule intermédiaire est “géométriquement” nécessaire pour prendre le relais avec une cellule polaire à branche descendante polaire. Dans chaque hémisphère on a alors une cellule “équatoriale” (dite cellule de Hadley), une cellule intermédiaire (dite cellule de Ferrel), et une cellule polaire.
Ces mouvements atmosphériques induisent une redistribution d'énergie des zones chaudes vers les zones polaires plus froides : cela atténue l'effet latitudinal de distribution de l'énergie solaire incidente mais accentue l'opposition saisonnière Nord-Sud puisque l'énergie solaire reçue au sol ne “traverse” pas l'équateur à court terme (du moins pas du fait de la redistribution latitudinale atmosphérique).
5. Récapitulatif – Le pourquoi des saisons
⇒ Il y a des saisons sur la Terre du fait de son obliquité non nulle, c'est-à-dire du fait que son axe de rotation n'est pas perpendiculaire au plan de l'écliptique mais est incliné d'environ ψ=23,4° par rapport à cette perpendiculaire.
⇒ Du fait de la rotation de la Terre sur elle-même, l'effet Coriolis sépare les masses d'air de part et d'autre de l'équateur. Ces mouvements atmosphériques induisent une redistribution d'énergie des zones intertropicales chaudes vers les zones polaires plus froides : cela atténue l'effet latitudinal de distribution de l'énergie solaire incidente mais accentue l'opposition saisonnière Nord-Sud.
6. Calculs simples et compléments
Excentricité et variation d'énergie reçue par la Terre
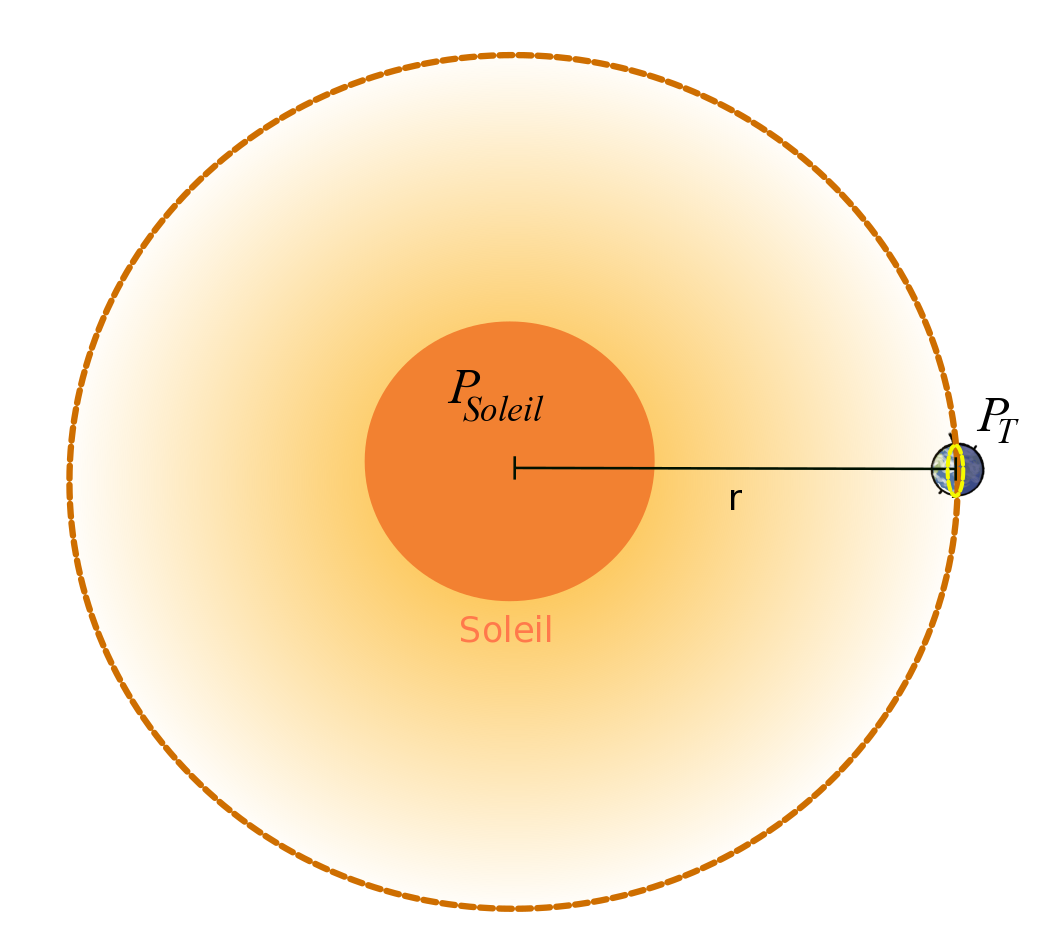
On note \(P_{Soleil}\) la puissance émise par le Soleil. La propagation a lieu dans toutes les directions. La puissance conservée se retrouve à la surface de toute sphère centrée sur le Soleil.
À une distance \(r\) du Soleil, la puissance \(p_{r}\) (appelée irradiance) puissance reçue par une surface perpendiculaire au rayonnement solaire, est : $$p_{r} = \frac{P_{Soleil}}{4 \times \pi r^2}$$
L'irradiance diminue donc avec le carré de la distance au Soleil.
Figure 19. Représentation de la puissance reçue par la Terre située à une distance \(r\) du Soleil La puissance totale captée par la Terre, de rayon \(R_T\), est égale à \(P_{T} = p_r \times \pi R_T^2\). Cela correspond à l'énergie solaire reçue sur un disque de rayon \(R_T\) (en jaune sur la figure. L'énergie reçue se répartit sur la demi-sphère éclairée mais, la Terre tournant sur elle-même, l'énergie est finalement répartie sur la surface de la sphère, surface égale à \( 4 \pi R_T^2\), surface 4 fois supérieure à la surface du disque terrestre. La puissance moyenne (jour/nuit, moyenne toutes latitudes) au sol est donc le quart de l'irradiance à la distance \(r\). On pourra aussi consulter Kartable [ref2] et Paillard (2020) [ref1]. |
On note \(p_{Tm}\) l'irradiance à la distance moyenne \(r_m\) de la Terre, \(p_{Ta}\) l'irradiance à l'aphélie et \(p_{Tp}\) l'irradiance au périhélie[1].
On a alors : $$\frac{P_{Soleil}}{4 \times \pi} = p_{Tm} \times r_m^2 = p_{Ta} \times r_a^2 = p_{Tp} \times r_p^2$$
Avec \(r_{m}\) = 149,6.109 m, \(r_{a}\) = 152,1.109 m et \(r_{p}\) = 147,6.109 m, on trouve donc :
\(p_{Ta}\) = 0,935 \(p_{Tp}\) (ou \(p_{Tp}\) = 1,069 \(p_{Ta}\)).
Soit une différence relative d'irradiance de moins de 7 % entre périhélie et aphélie.
Si l'on se réfère à la puissance moyenne :
\(p_{Ta}\) = 0,967 \(p_{Tm}\) et \(p_{Tp}\) = 1,034 \(p_{Tm}\).
Soit des variations de ±3,4 % d'énergie reçue par rapport à la situation moyenne.
Avec \(p_{Tm}\) = 1366 W.m−2[2], on a \(p_{Ta}\) = 1321 W.m−2 et \(p_{Tp}\) = 1412 W.m−2.
La température d'équilibre d'un corps noir est fonction de l'énergie reçue selon la relation \(E = \sigma T^4\), avec \(\sigma\) la constante de Stefan-Boltzmann. Ainsi, lorsqu'on multiplie l'énergie absorbée par un facteur c, la température (en K) est, elle, multipliée c1/4.
En prenant \(T_m\) = 288,1 K (15°C) correspondant à \(p_{Tm}\), alors on a \(T_a\) = 288,1×0,9671/4 = 285,7 K (12,6°C), et \(T_p\) = 288,1×1,0341/4 = 290,5 K (17,4°C).
Soit une différence potentielle de 4,8°C entre les températures d'équilibre à l'aphélie et au périhélie pour une température moyenne de 15°C. Notons que ce calcul est fait en considérant que toute variation de puissance reçue sur Terre n'affecte en rien les autres paramètres expliquant la température effective (albédo, effet de serre…). Ces températures d'équilibre extrêmes ne seraient théoriquement atteintes que quelques jours par an, elles ne sont que des indicateurs extrêmes (“l'équilibre” n'a pas le temps de se faire) mais elles permettent d'évaluer de combien au maximum les étés de l'hémisphère Sud [les hivers de l'hémisphère Nord], vers le périhélie, sont plus chauds que les étés de l'hémisphère Nord [les hivers de l'hémisphère Sud], vers l'aphélie.
Reprenons le raisonnement ci-dessus mais pour calculer cette fois la différence de puissance reçue selon la position sur le demi-globe éclairé, c'est-à-dire selon que l'on est sur le plan de l'écliptique “au plus près du Soleil”, ou 6370 km (rayon terrestre) plus loin, à la limite jour/nuit. Pour une distance Terre-Soleil moyenne de 149,60000 Gm prise pour la position “éloignée”, la position proche est alors à “seulement” 149,59363 Gm, d'où une différence de puissance relative de l'ordre de 85.10−6 (85 millionièmes). Pas de variation sensible de température à attendre dans ce cas !
Rotondité de la Terre et effet de la latitude sur la puissance reçue au sol
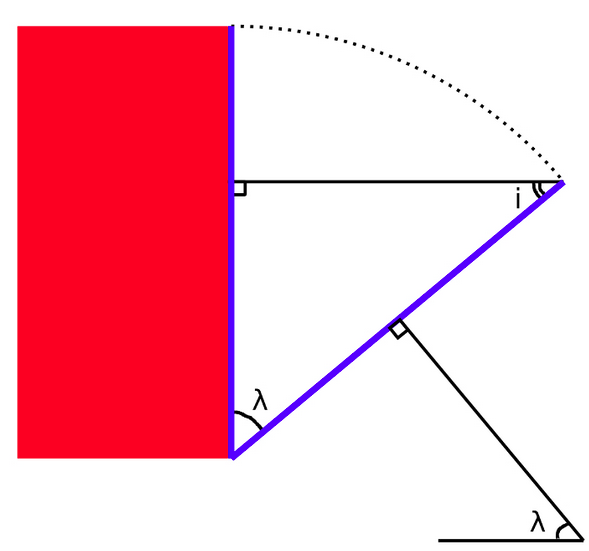
Dans la partie 2.2 Effet de la latitude on a raisonné à puissance solaire donnée, mais on peut aussi réfléchir à surface horizontale au sol fixe (figure 20). À midi, sur le plan de l'écliptique (donc à l'équateur dans le cas d'obliquité nulle), la surface au sol, perpendiculaire au rayonnement solaire (angle d'incidence maximal de 90°), “capte” l'énergie d'un faisceau solaire de référence. Lorsqu'on monte en latitude, λ, l'angle d'incidence, égal à 90°−λ, diminue. Une même surface au sol capte alors une portion de moins en moins importante du faisceau solaire de référence. Autrement dit, la puissance perçue par une surface donnée diminue lorsque la latitude augmente.
Figure 20. Puissance solaire reçue au sol en fonction de l'angle d'incidence L'angle d'incidence \(i\) est lié à la latitude \(λ\) par la relation \(i\)=90°−\(λ\). Par construction, la surface éclairée (hypothénuse) capte une fraction de faisceau solaire initial représenté par le côté opposé à l'angle \(i\) qui est aussi le côté adjacent à l'angle \(λ\). Cette fraction est donc égale à sin(\(i\)) ou cos(\(λ\)). La puissance solaire captée à midi par une surface donnée diminue lorsque l'angle d'incidence \(i\) diminue, c'est-à-dire lorsque la latitude \(λ\) augmente. |
On peut calculer que, par rapport à la puissance maximale \(P_{max}\) reçue au sol, à midi sur le plan de l'écliptique pour une latitude nulle, la puissance \(P_{λ}\) perçue à midi à la latitude \(λ\) est \(P_{Tλ} = cos(λ) \times P_{Tmax}\). On retrouve bien la puissance maximale pour \(λ\) = 0 avec cos(0) = 1 et une incidence \(i\) de 90°, et une puissance nulle à 90° de latitude avec cos(90) = 0 et un rayonnement solaire “rasant”, tangent à la surface du sol (incidence nulle).
Variation d'incidence au cours de la journée
La surface du sol est dans une situation de bascule selon un axe Est-Ouest perpendiculaire au rayonnement solaire de telle sorte qu'une surface perpendiculaire au rayonnement à midi “se couche” quand on monte en latitude (voir ci-dessus). De même, latéralement, entre le lever et le coucher du Soleil (de gauche à droite sur la vue de face) cette surface au sol s'incline plus ou moins selon un axe Nord-Sud perpendiculaire au rayonnement solaire. En se plaçant à l'équateur (écliptique), on a une incidence maximale à midi (90°) qui part de 0° au lever, passe par le maximum à midi et redescend à 0° au coucher du Soleil. Cette variation au cours de la journée, due à la rotation de la planète sur elle-même est de 15° de longitude par heure (pour une journée de 24h et donc une durée d'insolation de 12h). Ainsi, pour tout point de la sphère de latitude \(λ\) (0° sur l'écliptique) et de longitude \(φ\) (0° à la position méridienne), la puissance solaire relative au sol (par rapport au max à midi sur l'écliptique, c'est-à-dire au centre de la vue de face) est égale à \(cos((λ) \times cos(φ)\).
Répartition de l'énergie entre les deux hémisphères aux solstices
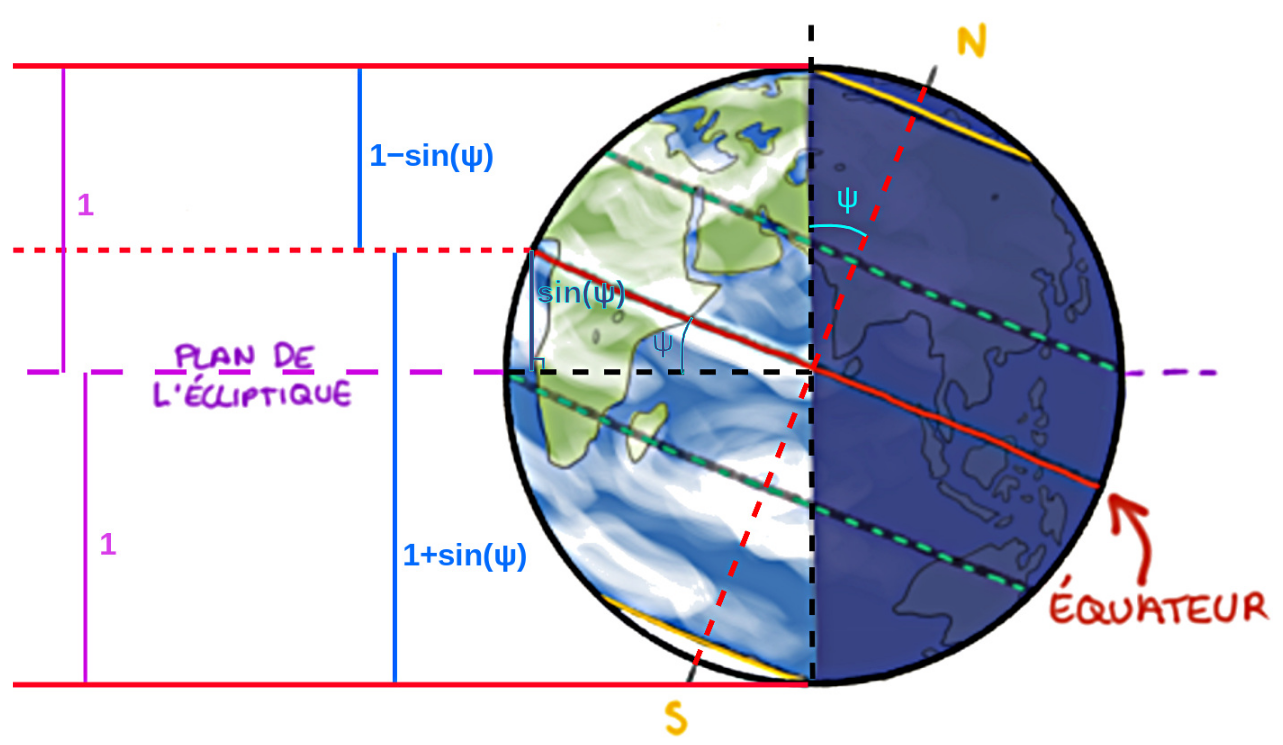
Au solstice de décembre (figure 21), l'hémisphère Sud reçoit la totalité du rayonnement solaire qui arrive sous l'écliptique, plus la fraction du rayonnement arrivant au-dessus de l'écliptique entre l'écliptique et l'équateur qui est alors à ψ = 23,4° au dessus de l'écliptique. Cette fraction correspond à sin(ψ) (figure 21). Au total, l'hémisphère Sud) reçoit donc une fraction de l'énergie solaire incidente égale à (1+sin(ψ))/2. Pour ψ = 23,4° on a, aux solstices, une énergie solaire répartie à 70% dans l'hémisphère en été et donc seulement à 30% pour l'hémisphère en hiver. L'hémisphère en été reçoit donc 2,33 fois plus d'énergie que l'hémisphère en hiver, rapport inversé 6 mois plus tard.
Figure 21. Répartition de l'énergie entre les deux hémisphères au solstice de décembre La même énergie arrive au Nord et au Sud de l'écliptique, mais l'hémisphère Sud “capte” (1+sin(ψ))/2 de l'énergie solaire éclairant le disque terrestre. |
Paramètres orbitaux et variations climatiques de longue période
Nous venons de voir que la rotondité de la Terre induit des climats latitudinaux, l'obliquité induit les saisons et l'ellipticité influence le contraste été/hiver (contraste actuellement amplifié au Sud et atténué au Nord). De plus, suivant la loi de Képler dite loi des aires, la durée des saisons est inégale. En effet, pour l'hémisphère Nord, la période hivernale du 21 septembre au 21 mars environ dure 181 jours, alors que la période estivale dure 184 jours (du 21 mars au 21 septembre environ).
Mais les paramètres orbitaux de la Terre varient au cours du temps avec des périodicités multi-millénaires.
L'obliquité ψ de la Terre varie ainsi d'environ 24,50° à 22,04° avec une périodicité de l'ordre de 41 000 ans. Ceci induit, par exemple, de légères variations de l'écart maximum d'énergie entre les hémisphères aux solstices (l'hémisphère estival reçoit alors de 68,8% à 70,7% de l'énergie solaire).
L'ellipticité est elle aussi variable. L'excentricité actuelle de la Terre est de 0,0167 ; lors des derniers millions d'années elle a varié de 0 à 0,06 avec des périodicités de 100 000 à 400 000 ans. Ceci induit des variations d'irradiance solaire entre périhélie et aphélie allant de 0% à environ 26%. Cela engendre donc des contrastes saisonniers plus ou moins importants pour les saisons proches de ces positions (actuellement l'été et l'hiver).
Si l'obliquité varie, l'orientation de l'axe de rotation varie aussi (il “tourne” autour de la perpendiculaire à l'écliptique). Cette rotation, dite précession des équinoxes, induit un changement de la position des équinoxes et des solstices sur l'orbite elliptique de la Terre. Le contraste saisonnier Nord/Sud est marqué pour l'été et l'hiver lorsque les solstices sont proches des positions de périhélie et d'aphélie, alors que ce contraste impacte printemps et automne lorsque ce sont les équinoxes qui sont proches de ces positions extrêmes. Ce lent déplacement s'effectue avec une périodicité proche de 26 000 ans.
Ces variations multiséculaires avec des périodicités de 20 à 400 milliers d'années ont été mises en évidence par M. Milankovitch car, en combinant leurs effets, elles expliquent les cycles glaciaires des derniers millions d'années. Les paramètres expliquant aujourd'hui les saisons sur Terre sont donc aussi importants pour comprendre les variations climatiques au cours des temps géologiques et plus précisément les glaciations/déglaciations successives du Quaternaire (de −2,5 Ma à aujourd'hui) [ref3, ref4, ref5].
Références
- [1] Didier Paillard, 2020. Climat et astronomie, Cahiers Clairaut, 170, 8-14
- [2] Calculer la puissance du rayonnement solaire reçu par la Terre, site Kartable
- [3] André Berger, Marie-France Loutre, 2004. Théorie astronomique des paléoclimats - Astronomical theory of palaeoclimates, C.R. Geoscience, 336, 7-8, 701-709 [pdf en archive ouverte]
- [4] Pourquoi la paléoclimatologie ?, C.R. Geoscience, 336 (2004) [numéro thématique, articles en archive ouverte]
- [5] Jacques Laskar, 1999. The limits of Earth orbital calculations for geological time-scale use, Phil. Trans. R. Soc. A., 357,1735–1759 [pdf]
- [6] Les mesures de l'irradiance solaire depuis 1978, site de l'ESA [irradiance moyenne de 1366 W.m−2]
- [7] Earth Fact Sheet, site de la NASA [compilation des paramètres physiques relatifs à la Terre]
[1] On note \(e\) l'excentricité de l'orbite terrestre, \(a\) et \(b\) les demi-grand et demi-petit axes, \(c\) la distance foyer-centre de l'ellipse. On a les relations : \(e = \frac{\sqrt{a^2-b^2}}{a}\) et \(e = \frac{c}{a}\).
Les distances à l'aphélie et au périhélie sont respectivement \(r_p = a-c\) et \(r_a = a+c\). On peut alors définir l'excentricié par la relation \(e = \frac{r_a-r_p}{r_a+r_p}\).
Pour citer cet article :
Les saisons sur Terre, répartition de l'énergie solaire et paramètres orbitaux, Delphine Chareyron, Olivier Dequincey, février 2022. CultureSciences Physique - ISSN 2554-876X, https://culturesciencesphysique.ens-lyon.fr/ressource/saisons.xml